一類廣義Petersen圖的Wiener指標

李伊昊，紅 霞

(洛陽師范學院 數學科學學院，河南 洛陽 471022)

0 引 言

本文所指的圖均為無向簡單圖，沒有給出說明的符號同文獻[1]。設G=(V，E)是有n個頂點的簡單連通圖，其中V=V(G)和E=E(G)分別為頂點集和邊集。對于任意2個頂點u，v∈V(G)，兩點間的距離d(u，v)為u和v之間的最短路徑長度，記為dG(u，v)。1947年，H.Wiener[2]首次提出了指標的概念。它不僅是圖論領域中的重要參數，而且在化學領域中能夠準確反映出分子圖的特征和性質。基于很多領域內的應用，學者們開始關注Wiener指標，到目前為止研究了很多相關結果。李建喜等[3]給出了單圈圖的Wiener指標和外圍Wiener指標的計算公式；邵云[4]研究了單圈圖的平均Wiener指標。蘇曉海[5]研究了單圈圖的邊平均Wiener指標。吉亞迪[6]等人研究了圖Ln的Wiener指數和Gutman指數，這里Ln表示n個六邊形和2n個正方形構成的線性結構分子圖。李丹怡等[8]考慮了雙繁星的Wiener指標的極值問題，本文主要研究一類廣義Petersen圖的Wiener指標的計算公式。

1 基本概念

定義1[2]Wiener指標為圖G中無序點對的距離之和，并記為W(G)，即

W(G)=∑{v，u}?V(G)dG(v，u)

定義2[7]設廣義Petersen圖G=P(n，k)，n≠2k， 是2n個頂點的圖，其頂點集和邊集分別為

V(G)={u1，u2，…，un，v1，v2，…，vn}
E(G)={vivi+k(mod n)，uivi，uiui+1(mod n)|i=1，2，…，n}

2 主要結果

定理1設G=P(n，2)，n≥5，則

證明設G=P(n，2)，n≥3，圖G的頂點集合和邊集合如定義2所示。下面分4種情況來討論G的Wiener指標W(G)。

情況1當n≡0(mod4)且n≥8時，對于給定頂點vi到其它頂點vj(j≠i)的距離有

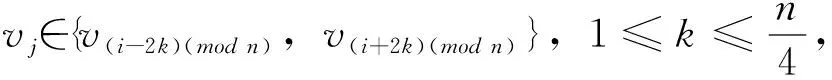
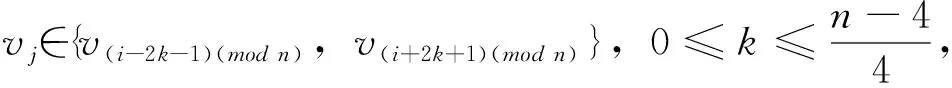
從而頂點vi到其它頂點vj的距離之和為

再由圖G的結構對稱性，走遍所有頂點vi(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點uj(j≠i)的距離有

若uj∈{u(i-k)(mod n)，u(i+k)(mod n)}，1≤k≤4，則dG(ui，uj)=k

從而頂點ui到其它頂點uj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點vj的距離有

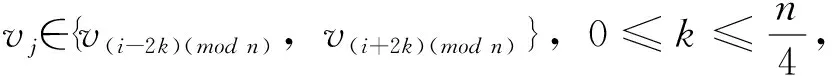
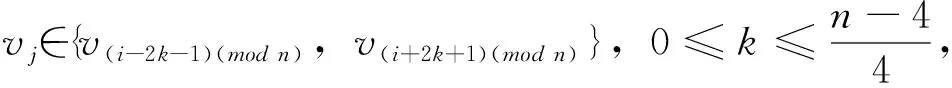
從而頂點ui到其它頂點vj的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

綜上所述，有

W(G)=W1+W2+W3

情況2當n≡1(mod4)時，容易計算，若n=5，則W(G)=75。若n=9，則W(G)=360。

若n≥13，對于給定頂點vi到其它頂點vj(j≠i)的距離有

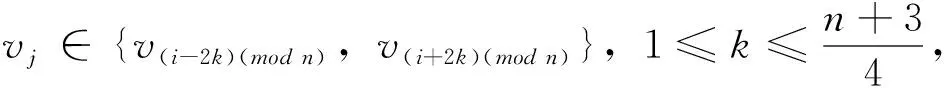
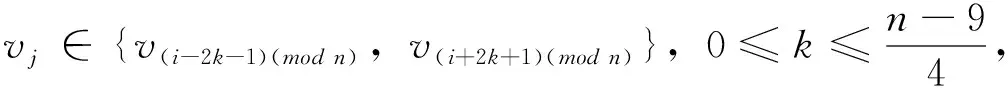
從而頂點vi到其它頂點vj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點vi(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點ui(j≠i)的距離有

若uj∈{u(i-k)(mod n)，u(i+k)(mod n)}，1≤k≤4，則dG(ui，uj)=k

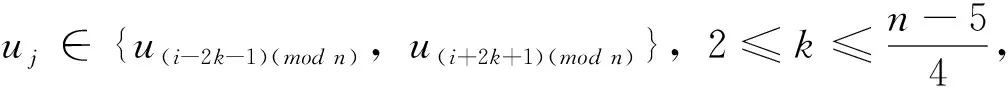
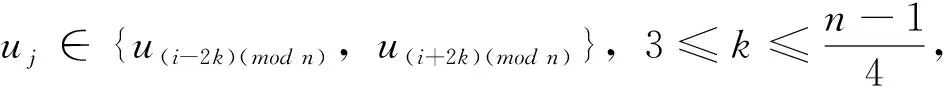
從而頂點ui到其它頂點uj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)， 得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點vj的距離有

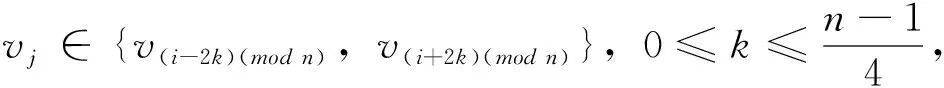
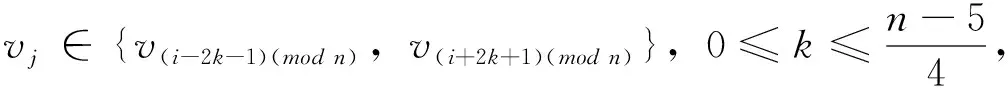
從而頂點ui到其它頂點vj的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)， 得出任意2個不同頂點之間的距離之和為

綜上所述，有

W(G)=W1+W2+W3

情況3 當n≡2(mod4)時，容易計算，若n=6，則W(G)=135

若n≥10，對于給定頂點vi到其它頂點vj(j≠i)的距離有

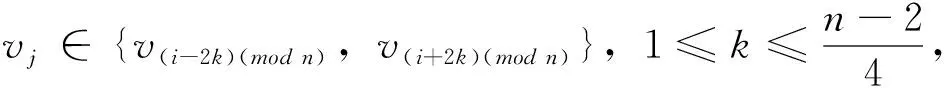
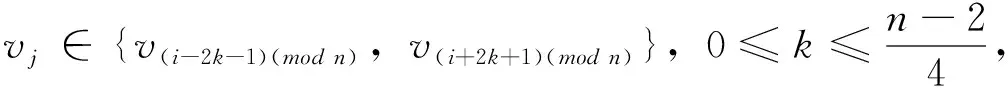
從而頂點vi到其它頂點vj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點vi(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點uj(j≠i)的距離有

若uj∈{u(i-k)(mod n)，u(i+k)(mod n)}，1≤k≤4，則dG(ui，uj)=k

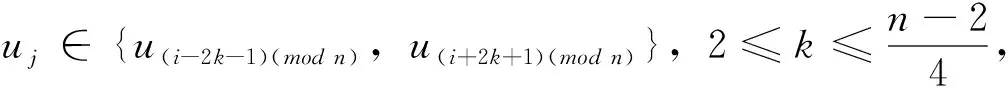
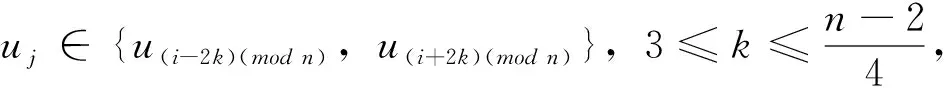
從而頂點ui到其它頂點uj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)， 得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點vj的距離有

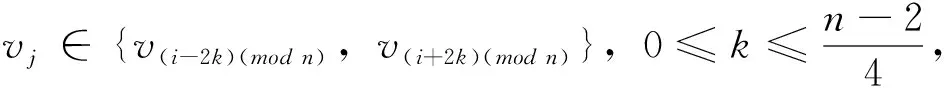
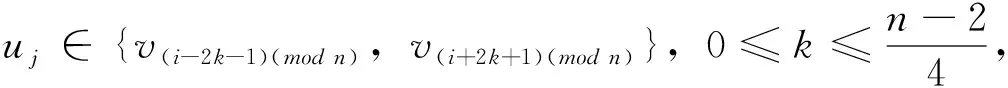
從而頂點ui到其它頂點vj的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

綜上所述，有

W(G)=W1+W2+W3

情況4 當n≡3(mod4)時，容易計算，若n=7，則W(G)=189。

若n≥11，則對于給定頂點vi到其它頂點vj(j≠i)的距離有

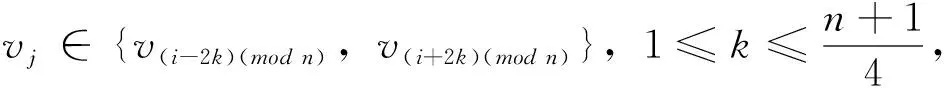
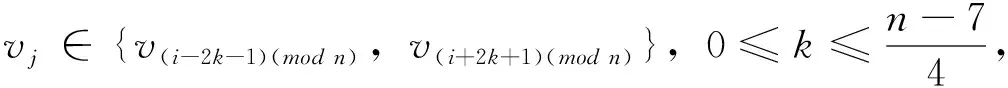
頂點vi到其它頂點vj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點vi(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點uj(j≠i)的距離有

若uj∈{u(i-k)(mod n)，u(i+k)(mod n)}，1≤k≤4，則dG(ui，uj)=k

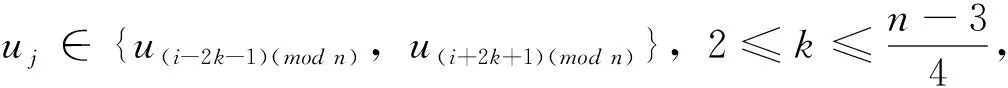
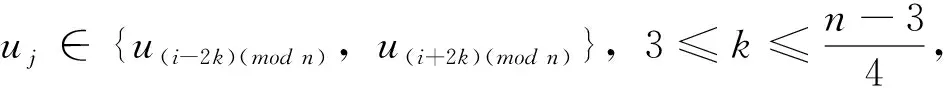
頂點ui到其它頂點uj(j≠i)的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)， 得出任意2個不同頂點之間的距離之和為

對于給定頂點ui到其它頂點vj的距離有

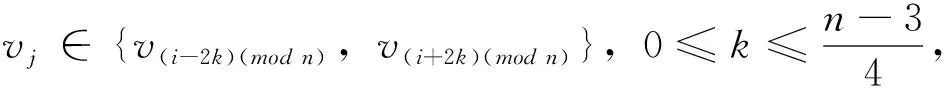
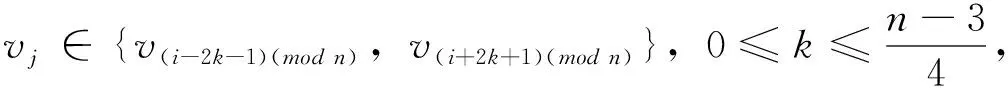
從而頂點ui到其它頂點vj的距離之和為

再由圖G的結構對稱性，走遍所有頂點ui(1≤i≤n)，得出任意2個不同頂點之間的距離之和為

綜上所述，有

W(G)=W1+W2+W3

根據以上1、2、3、4情況，定理結論成立。定理1證畢。

3 結 論

廣義Petersen圖是一類重要的并被廣泛研究的互聯網絡拓撲結構，而Wiener指標作為一個重要的拓撲指數在化學研究中用來研究分子的結構。本文主要研究了廣義Petersen圖的Wiener指標。該研究方法還可以計算出更多三正則圖類。同時也可以啟發進一步探索對稱性較強的圖類的Wiener指標的計算問題。