基于改進ACO算法的工程項目物流成本管理應用研究

張佑健，李 莉，吳 瑕，狄宏林

(1.東莞開放大學，廣東 東莞 523000；2.惠州學院，廣東 惠州 516007)

0 引 言

在電力市場中，電網企業為了能夠提高其市場競爭力，企業的管理模式需要發生改變，轉移到以經濟效益為中心[1-3]。而其涉及的物流管理模式影響著企業的成本控制、經濟效益等方面。因此，在進行電網企業成本控制時，可以對其工程項目物流成本進行降低，以此來降低企業成本，提高競爭力。然而，在當前電網企業成本管理中，相關工程造價制度并未涉及物流成本科目，使得企業對工程項目物流成本的掌控難度較大。如此一來，便對施工管理形成一定阻礙，不利于提高施工管理水平，從而影響電網企業經濟效益。有些學者面對集裝箱碼頭成本管理時，在時間驅動的基礎上，提出了改進作業成本法(activity-based costing approach，ABC)，能識別貨物裝卸過程的瓶頸，以及計算其裝卸成本，并全面分析相關物流活動及成本，結果表明了該方法的有效性[4]，因此，文章將ABC法應用在電網企業工程項目物流成本分析中。面對既有鐵路的優化設計問題，蟻群算法(ant colony optimization，ACO)發揮其空間組合優化性能，進行最優交點組合尋找。結果顯示，該算法的應用效果不錯[5]。因此將其應用在電網企業項目管理中，對項目物流成本進行優化，以期降低工程項目物流成本。

1 基于ABC算法和改進ACO算法的電網工程項目物流成本優化研究

1.1 ABC算法在工程項目物流成本模型構建中的應用

在電網企業項目管理中，以往的物流管理模型不再適應當前的發展需求，需進行管理方式的轉變。通過優化工程項目物流成本，降低經營生產成本，以此來獲得更強的市場競爭力。在一個電網工程項目全壽命周期中，包含了許多的物流工序，這些工序包含的工期和成本不同，通過相關邏輯關系形成了工程項目的物流成本。想要降低物流成本，就需對每道工序的工程、成本進行優化，從而解決工期-成本問題(time-cost-trade-off-problem，TCTP)。對TCTP進行分析，首先，確定每個物流工序實施方案。并對項目工期-成本的關系進行確定，畫出均衡曲線。其中物流工期目標的數學表達式見式(1)。

(1)

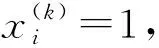
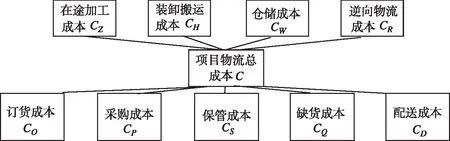
圖1 項目物流成本

圖1中，物流成本有訂貨成本等9種成本組成，從而得到項目物流成本C計算公式見式(2)。

(2)

式(2)中，i′為選擇的方案，方案總數是m。處理工期與成本采用無量綱化處理方式，得到物流成本優化模型目標函數，相關公式見式(3)。

Z=C+T

(3)

式(3)中，Z表示目標函數。在模型中，想要解決TCTP，便需從零列到n列的線路中，獲取一條線路，使成本目標和工期最小。在物流成本中，合適的核算辦法可以明了物流各流程的成本花費情況，知曉物流過程的瓶頸。對此，文章采用ABC法。有別于以往的成本分析法，ABC法的潛在假設是因生產產品或提供服務出現了作業活動，在該活動中會產生費用成本。該方法能夠對整個項目物流成本構成進行分析，給出的相關費用信息更精準。在該項目物流中，起始于物料供應商，通過不同物料環節的運輸等操作，最終達到施工現場，并進行相關組裝工作。期間，涉及的作業活動均屬于物流鏈，這些活動消耗的資源費用匯總起來，并形成了物流成本。在ABC法中，包含了圖1中的9種成本的費用情況，具體如圖2所示。

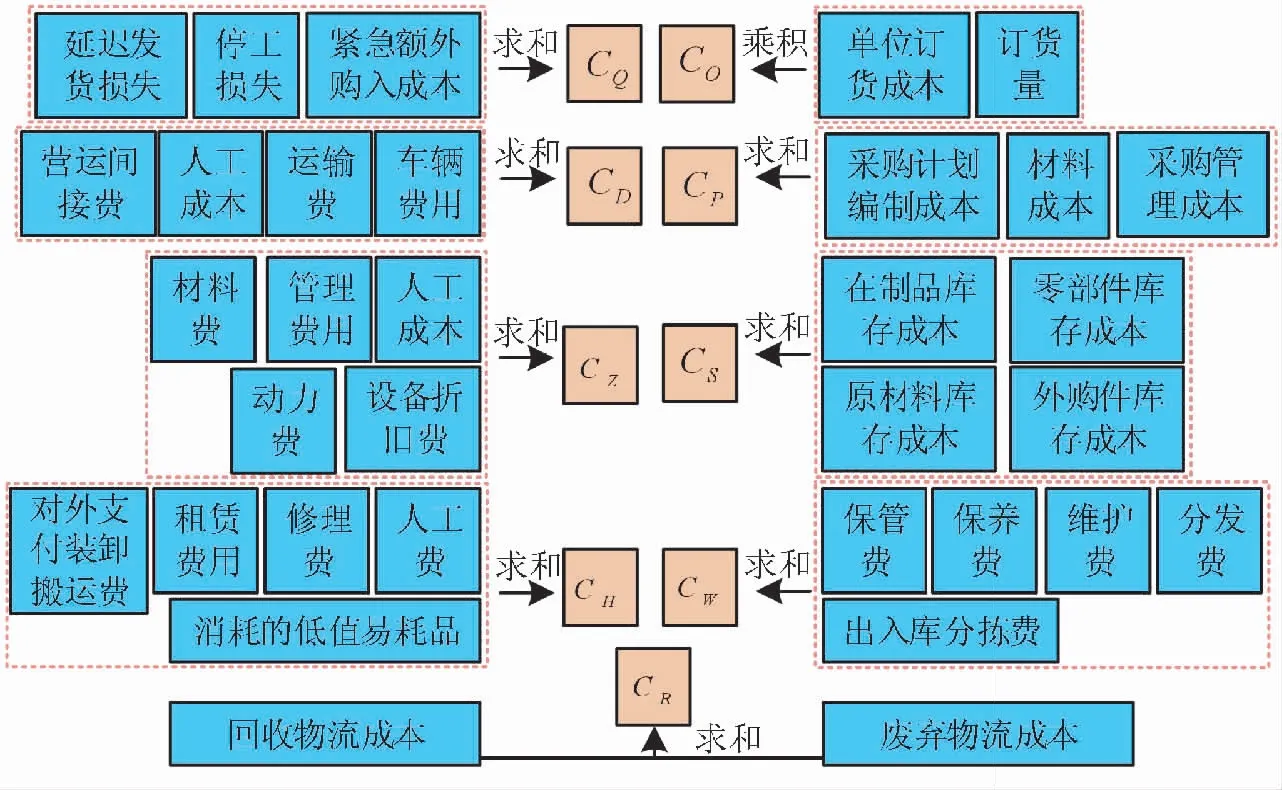
圖2 相關物流成本情況

從圖2中，可以知道不同物流模式的物流成本，根據對應的計算公式得到相應的物流成本，為物流成本優化做準備。在物流工序中，不僅要計算物流成本，還需對工期進行計算。在電網工程項目實施過程中，由于施工工藝難度大等不定因素的影響，易增大建設工期風險。想要更高效地完成項目中的物流過程，需對期間的工期計算模型進行構建。考慮到多因素制約的情況，文章將不可變因素設置成限制條件，而優化目標是可變因素，從而進行相關合理工期的確定，最終得到正常狀態下物流總工期，見式(4)。

T=min(tj-ti)，tj-ti≥ttjr，tj≥ti，ti≥0，i∈[1，n-1]

(4)

式(4)中，設置工序ij的開始時間、結束時間、正常完工時間分別為ti、tj、ttjr，也就是說tijr是工序ij的工序期望值。

1.2 改進ACO算法在工程項目物流成本優化中的應用

在構建了項目物流成本模型后，對模型進行優化。該問題屬于組合優化問題，而ACO算法在該類型問題求解上具有較好的性能，因此，文章選取ACO算法，解決物流成本優化問題[6-7]。在問題解決的過程中，將其轉化成旅行商問題。由于算法的信息素發揮因子會較大程度地影響算法的運行情況，使全局搜索能力及收斂速度發生較大變化，因此，可以利用修正自適應權重法進行算法優化。其中工期和成本目標的權重見式(5)。

(5)

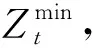
(6)

式(6)中，f(X)表示綜合目標值，將一次循環產生的解的序號設置成X，第X個解的成本目標值設置成Zc，該解的工期目標值設置成Zt，r表示隨機數，均布的范圍為[0，1]，為防止f(X)出現零或無效值的情況，一次循環后，對路徑τ更新值進行計算。對各邊的信息素揮發度進行更新，對螞蟻選擇各邊的概率進行計算，見式(7)。

(7)

式(7)中，i、j1、j2分別表示當前工序、下次工序、下下次工序的實施方案序號，α、β表示參數，α、β可以分別對信息素、路徑的相對重要程度進行控制，將邊(i，j1，j2)可見度設置成ηi，j1，j2，代表搜索過程中的局部信息。通過ACO算法給蟻群的螞蟻選擇路徑，具體見式(8)。

(8)

式(8)中，J表示確定的概率進行選擇，q表示隨機數，其均布的范圍為[0，1]，q0是[0，1]中的參數。把搜索的新解放至解庫，對E進行更新，重復分配vc、vt與更新E之間的步驟，直到滿足終止條件位置。由此可得物流成本優化的流程見圖3。

圖3 物流成本優化流程

2 基于改進ACO算法的電網工程項目物流成本優化應用分析

對文章使用方法進行驗證，數據來源于某高壓輸變電工程造價項目現有數據和某物資公司提供的相關數據，經過模擬后得到文章所需的項目物流成本數據，這些數據可反映項目物流成本特點。在項目物流成本中，擁有的工序為9個，這些工序包括訂貨、采購、倉儲等內容，每個工序有5個備選方案。首先，通過收集的項目實際數據，獲取每個工序物流成本與工期的關系，對物流成本進行模擬，將得到的相關數據設置為樣本。通過改進ACO算法，對項目物流成本目標函數的最優解進行搜索。由于參數會對改進ACO算法最優解搜索速度造成影響，因此，選取合適的參數較為重要。設置螞蟻參數為m，設置信息素揮發度為ρ，將信息、期望兩種啟發式因子分別設置為α、β，信息素總量為Q=1，設置最大迭代為80。首先，設置m=30，ρ=0.7，研究不同α、β組合下算法的性能情況，如圖4所示。

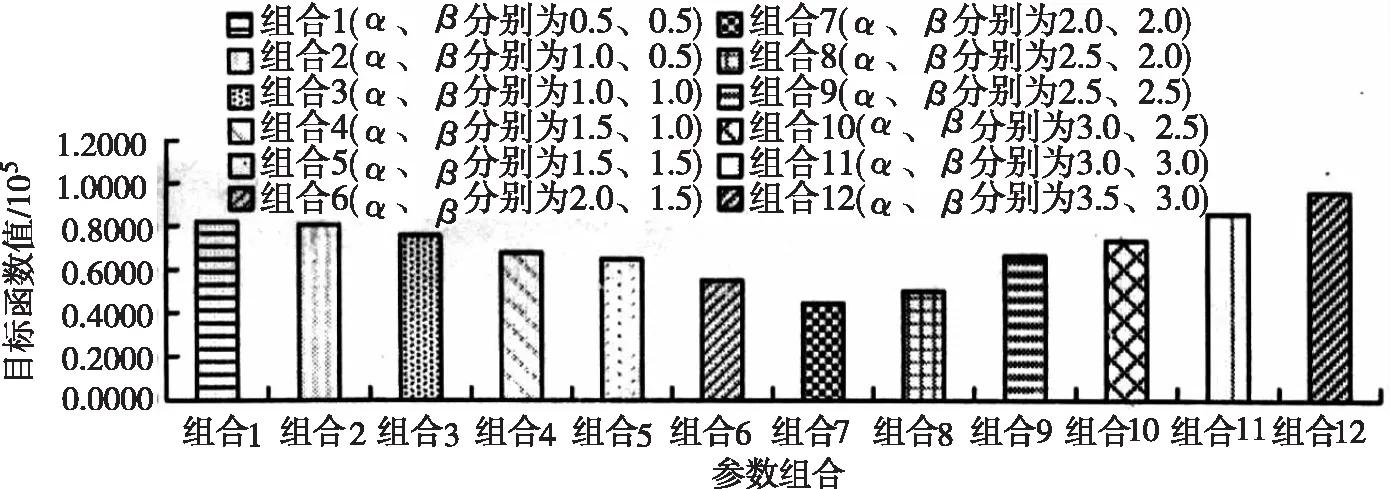
圖4 不同、組合下算法的性能

圖4中，不同α、β組合下改進ACO算法的目標函數值不同，算法目標函數值最小的組合為組合7，該組合的算法目標函數值為0.4434*105，根據物流成本最小化的要求，組合7對應的α、β值符合要求，即算法參數α、β取值應分別以該參數為基礎，研究不同螞蟻數下改進ACO算法的目標函數變化情況，如圖5所示。

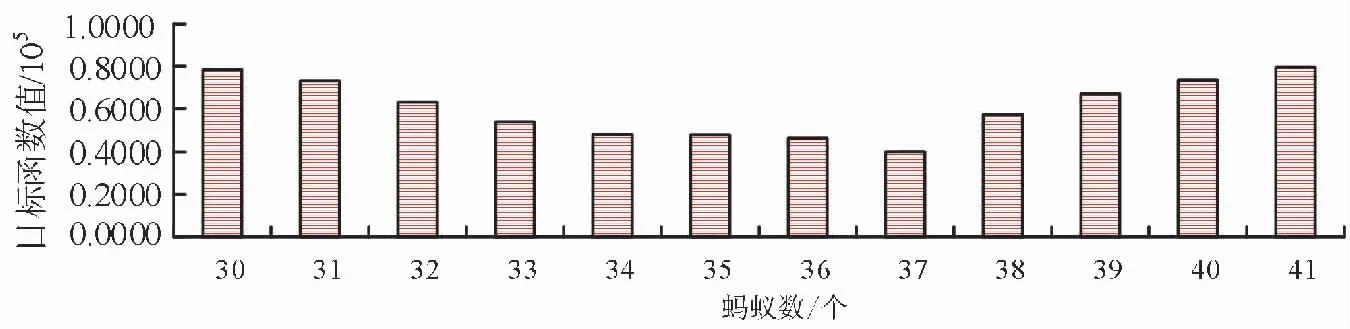
圖5 不同螞蟻數下改進ACO算法的目標函數值

圖5中，隨著螞蟻數的增加，改進ACO算法的目標函數值先逐漸降低后逐漸提高。改進ACO算法目標函數最小時對應的螞蟻數為37，此時的目標函數值為0.4008*105。根據目標函數值大小可知，螞蟻數取值為37時，最符合要求，因此將其作為改進ACO算法最終確定的螞蟻數。在此基礎上，研究不同信息素揮發度ρ下改進ACO算法的目標函數變化情況，如圖6所示。

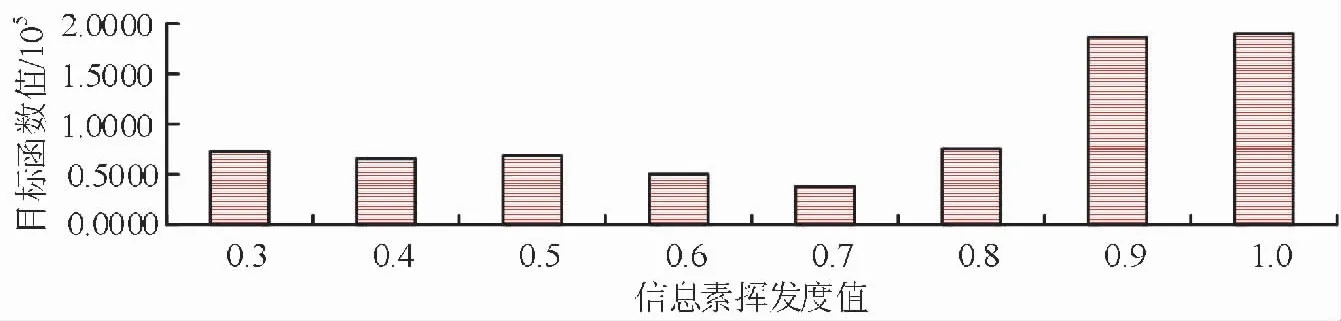
圖6 不同信息素揮發度下改進ACO算法的目標函數值

圖6中，隨著信息素揮發度的增大，改進ACO算法目標函數值先逐漸減小后迅速增大。從目標函數值大小可知，信息素揮發度取值為0.7時，最符合要求，此時可獲得最小的物流成本。因此，將其作為最終的信息素揮發度值，從而確定了ACO算法最終的α、β、m、ρ值。參數確定后，研究該算法在不同函數下的適應度值與運行時間如圖7所示。

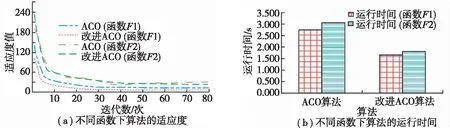
圖7 不同函數下算法的性能

圖7a中，函數不同，兩種算法的適應度不同；同一函數下，迭代數不同，算法適應度不同。在函數中，改進ACO算法適應度曲線總位于ACO算法下方，且前者比后者先出現收斂情況。圖7b中，不同函數下算法的運行時間不同。在函數F1中，改進ACO算法的運行時間為1.657 s，比ACO算法少1.089 s；在函數F2中，改進ACO算法1.809 s。由此可見，改進ACO算法性能更佳。設置最大迭代為80，ACO算法為對比算法，研究文章使用的改進ACO算法和ACO算法在電網工程項目物流成本優化中的應用結果，相關內容如圖8所示。

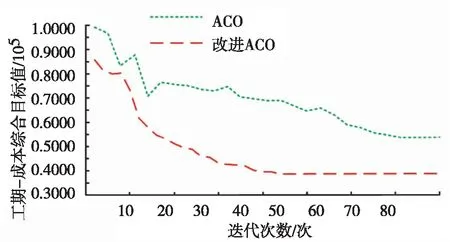
圖8 兩種算法的應用結果

圖8中，隨著迭代次數的增加，改進ACO算法和ACO算法的工期-成本綜合目標值呈下降趨勢，并最終穩定下來。從算法對應的折線圖可以看出，改進ACO算法對應的折線圖位于ACO算法的下方，即相同迭代下改進ACO算法的工期-成本綜合目標值總是小于ACO算法。當迭代次數為20時，改進ACO算法的工期-成本綜合目標值為0.50817*105，比ACO算法小0.2491*105；當迭代次數為40時，改進ACO算法和ACO算法的工期-成本綜合目標值分別為0.3988*105和0.6952*105。當迭代次數為45時，改進ACO算法的工期-成本綜合目標值為0.3790*105，且為其收斂迭代次數；而ACO算法的收斂迭代數為72，該算法的工期-成本綜合目標值為0.5319*105，ACO算法的收斂迭代數比其少27，明顯比改進ACO算法大。由此可見，改進ACO算法優于ACO算法。

3 結 論

為降低電網企業工程項目物流成本，實現企業項目優化管理，文章在TCTP的基礎上，構建工程項目物流成本模型，利用ABC法核算該模型，并通過進行物流工序工期的計算。在工程項目物流成本模型優化中，將TCTP轉換為旅行商問題，將自適應權重和ANN算法融入到ACO算法中，對ACO算法進行改進，以此來提高算法全局收斂能力，并將該算法應用在工程項目物流成本優化中。結果顯示，α、β、m、ρ值會較大影響改進ACO算法的性能。固定其他參數，在組合7中，算法目標函數值最小為0.4434*105，即算法參數α、β最佳取值均為0.2。固定其他參數，螞蟻數為37，最小目標函數值為0.4008*105，即螞蟻數m最佳取值為37。固定其他參數，當信息素揮發度為0.7，對應的目標函數值最小為0.3790*105，即ρ=0.7為最佳信息素揮發度。在不同函數下算法性能檢測中，改進ACO算法的收斂性更好、運行時間更短，在函數F1中，改進ACO算法的運行時間為1.657 s。在參數確定后的改進ACO算法應用分析中，改進ACO算法優于ACO算法，其收斂迭代數更少，為45，工期-成本綜合目標值更小，為0.3790*105。由此可見，文章采用方法應用效果較好。在今后，還可以進行更多約束條件的設置，進一步縮小項目物流成本與實際情況的差距。