“小數乘整數”課例研究

文| 韓 薇

【教學內容】

蘇教版五年級上冊第55 頁例1。

【教材分析】

知識分析：本節課是在學生掌握了整數四則運算、小數的意義和性質，以及小數加、減法的基礎上進行教學的。小數乘整數的學習也為以后小數乘小數的學習打下基礎，小數乘法的計算在日常生活中有廣泛的應用。由于小數和整數都遵循十進制計數法的位值原則，小數乘整數的豎式形式、順序都可以仿照整數乘法的規則進行，所以本節課引導學生將整數乘法的經驗遷移到小數中來。

方法分析：如果我們以發展的眼光看問題，那么小數乘整數相關知識的學習、算理的理解、轉化方法的歸類不僅僅影響小數乘法相關知識，還會對小數除法如小數除以整數產生影響，也會對分數乘法中分數乘整數算理的理解、算法的分析產生重要的影響。

【教學過程】

一、創設情境，導入新課

師：同學們，你們喜歡吃哪些水果？這些水果一年四季都可以吃到嗎？隨著農業生產技術的不斷進步，很多水果一年四季都可以種植、收獲了。不過，它們的價格也會隨著季節的變化而變化。

（出示例1）

師：從圖中你能獲得哪些信息？

生：可以從圖中得知西瓜每千克0.8 元，買了3 千克的西瓜。

師：夏天是西瓜豐收的季節，那么買3 千克西瓜要多少元？你能列出算式嗎？

生：列式為0.8×3。

師：為什么要用乘法呢？

生1：單價×數量=總價。

生2：因為買3 千克的西瓜就表示3 個0.8 相加。

師：看來小數乘整數與整數乘法的意義是相同的，都是在求幾個相同加數的和。

師：這道算式與以前學習過的算式有什么不同呢？

生：以前學習的乘法中，乘數都是整數，這個乘法算式中，乘數中有小數。

師：是的，這就是我們這節課要學習的內容。（板書課題：小數乘整數）

【設計意圖：充分利用教材提供的問題情境，引導學生從喜歡吃什么水果這個話題逐步展開交流，從而引出有些水果的價格會隨著季節的變化而變化，并由此提出相關數學問題，這樣安排既能使學生初步體會小數乘法與整數乘法的聯系，又能充分體會小數乘法與日常生活的密切聯系，還能使他們十分自然地融入新知的學習過程。】

二、自主探究，理解算理

1.探究0.8×3

師：用你喜歡的方法計算0.8×3。可以畫一畫、寫一寫、算一算，把你的想法記錄在《學習單》中。

（學生在黑板上板演不同的解答方法）

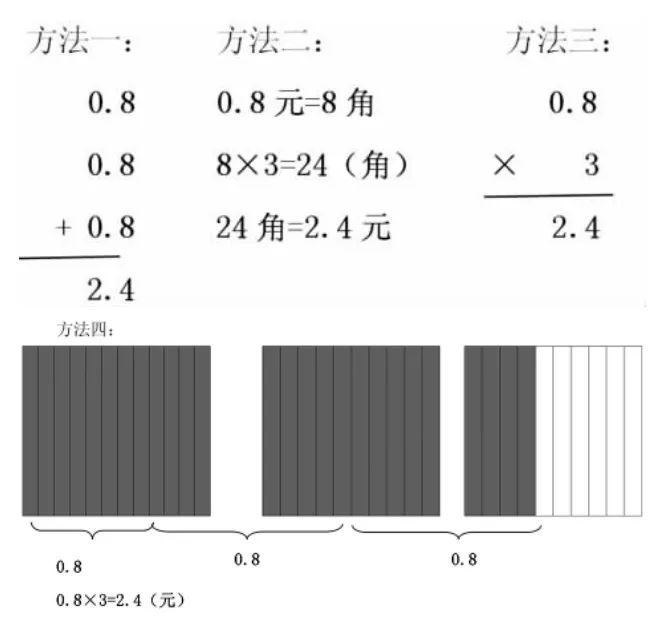
師：仔細觀察每一種方法，都能看懂嗎？哪些方法之間有聯系？小組進行討論。

生：方法一、方法三和方法四有聯系，它們的意義相同，都是在求幾個相同加數的和。

生：方法一、方法二和方法四有聯系，都是將新知識轉化成已經學習的知識解決問題。

生：這四種方法都是在計算計數單位的個數。

生：我也發現了，方法一、方法三和方法四中，0.8 可以看成是8 個0.1，3 個0.8 相加就是24 個0.1 也就是2.4；方法二中，先把0.8 元看成8 角，3 個8 角的和是24 角也就是24 個0.1 元，是2.4元。所以這四種方法的共同點都是在計算計數單位的個數。

師：通過同學們的不斷思考發現了四種方法的共同點，這就是小數乘整數的算理，本質就是在計算計數單位的個數。（板書：計算計數單位的個數）

師：如果再讓你做一道計算題，你會選擇哪種方法呢？

生：我喜歡用豎式計算，因為比較簡單。

師：看來再遇到這類計算時，我們可以列豎式進行計算。

【設計意圖：學生利用已有的知識和經驗，分析方法之間的聯系，側重引導他們聯系小數的意義，從計數單位的角度再次分析計算的結果，不僅讓學生更加透徹的理解算理，而且溝通了小數乘法與整數乘法的聯系，都是在計算計數單位的個數。四種方法都是轉化成已有知識來解決新問題，讓學生體會“轉化”思想在解決問題中的重要性，感悟數學知識發生發展的內在邏輯。】

2.探究0.8×3 的筆算方法（解決對位問題）

師：觀察三種方法，你還有什么疑問嗎？

生：方法三中的豎式不對，乘數3 應該和0.8 的0 對齊。

師：剛剛大家在解答題時，確實看到這兩種情況，你認為哪個正確呢？

生：第二個正確，因為小數的加法和減法都是要小數點對齊，所以我認為小數乘整數也是小數點對齊。

生：第一個正確，在進行計算時，把0.8 當做8，按整數乘法去計算，算出有24 個計數單位，也就是2.4，所以3 要和8 對齊。

師：是的，我們可以這樣看。

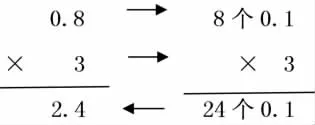
師：同學們，你們現在知道哪種方法正確了嗎？

生：第一種是正確的，我發現計算小數乘整數時，先按整數乘法進行計算，再去確定小數點的位置。

3.嘗試計算2.35×3，進一步理解算理

師：冬天到了，西瓜的單價發生變化，還是買3 千克，請你估一估大約需要多少元呢？

生1：6 元多，因為把2.35 看成是2 元，2×3=6，2.35＞2，所以是6 元多。

生2：把2.35 元看成是2.4元，大約需要7 元多。

生3：把2.35 元看成3 元，最多不會超過9 元。

師：在沒有進行計算時，我們也可以用估算的方法，得知得數大概的范圍。到底需要多少元呢？讓我們嘗試著用豎式算一算。

（請一學生到前面板演。學生完成后，請板演同學詳細講解計算過程，并互動質疑，弄清算理）

【設計意圖：請學生嘗試計算前先估算，不僅可以培養學生的數感，也可以幫助學生理解算理，而“嘗試計算”也給了學生更大的學習空間與思考的自由。先算235×3 得705，讓學生說一說其實是算了多少個多少？那么結果為什么是7.05 呢？一個問題指向算法，一個問題指向算理，算法與算理并行，進一步理解算理，總結計算方法。】

三、初用方法，促進內化

師：說說第（1）小題先看成多少乘多少，再說說積分別是幾位小數。

生1：先看成37×5=185，也就是有185 個0.1，所以得數是18.5。

生2：先看成18×6=108，也就是有108 個0.01，所以得數是1.08。

師：第（2）小題中積的小數點的位置對嗎？（依次出示）

生1：第一個小數點要對齊。

生2：老師，我認為他說得不正確。不是因為小數點對齊，而是因為表示5712 個0.01，就是57.12，所以小數點的位置在1 和7 之間。

生3：第二個小數點的位置不正確，1484 表示有1484 個0.1，就是148.4。

生4：第三個的積表示42 個0.01，就是0.42，應該在4 前面補0，再添上小數點。

生5：第四個從第一個乘數可以知道最后算出的積是多少個0.01，所以積應該是個兩位小數。

師：是的，只要掌握了小數乘整數的算理，就算沒有數字，根據它的本質，也可以判斷出小數點的位置，你們真是太厲害了。

【設計意圖：根據第（1）小題的練習，鞏固小數乘整數的方法；第（2）小題確定小數點的位置，四道習題層層遞進，最后一道方格題，幫助學生建模，理解小數乘整數時小數點的位置。】

四、比較分析，獲得算法

師：比較算式，看看積的小數位數與積中乘數的小數位數之間有什么關系呢？

生1：第一個乘數有幾位小數，積就有幾位小數。

生2：我發現第一個乘數都是小數，第二個乘數都是整數。

生3：在小數乘整數中，乘數有幾位小數，積就有幾位小數。

師：同學們，你們真厲害，不僅明白了小數乘法的算理，還通過觀察比較發現了在小數乘整數中，乘數有幾位小數，積就有幾位小數。誰能說說列豎式計算小數乘整數的方法呢？

生：先按整數乘法進行計算，將數的末尾對齊；接下來確定得數小數的位數，乘數有幾位小數，就從積的右邊起數出幾位，點上小數點。

【設計意圖：在學生自主研究、嘗試計算的基礎上，引導學生初步猜想 “積的小數位數與乘數的小數位數之間的關系”，把學生的注意力由算理及時轉向算法，從而為算法的抽象積累感性經驗。】

五、總結評價，交流提升

師：通過這節課的學習，你有什么收獲？

【設計意圖：計數單位的架構：理解整數、小數、分數四則計算都是在計算計數單位的個數。轉化思想架構：不管是運算的轉化，還是數的轉化、形的轉化、解決問題的轉化，都是運用已有知識來解決新的問題。方法架構：打通整數乘法與小數乘法的關系。】

【反思】

一、溝通比較，進行計數單位的架構

本課在教學過程中注重計算方法的多樣化，根據方法之間的內在聯系，溝通比較明析算理，凸顯小數乘法算理和算法的本質，從而體會數的運算的一致性。得出整數、小數、分數四則計算都是在計算計數單位的個數。

二、分析體會，進行轉化思想的架構

在多種算法的分析比較中，感受方法的共同性，從而滲透轉化思想。讓學生體會到，不管是運算的轉化、數的轉化、形的轉化還是解決問題的轉化，都是運用已有知識來解決新的問題。

三、總結提升，進行計算方法的架構

在練習中，獲得算法，促進知識內化，打通整數乘法與小數乘法的關系。

本節課也有遺憾，在解決對位問題時讓學生體會得還不夠。應該再次聯系舊知，讓學生回顧，以前的學習中有沒有不是相同數位對齊的情況，通過回顧溝通“300×4”時采用的“隔0 大法”與小數乘整數的對位方法，再次體會計算的本質，加以深刻理解。