關于“數字信號處理”課程“圍線積分法”求z 反變換思政教學的研究和探索

陳兆學，丁佳語，盧永祿

（上海理工大學健康科學與工程學院，上海 200093）

1 引言

由于相關實踐探索和教研經驗的缺失，目前在理工科實施“課程思政”教學，存在較大的難度，而對《數字信號處理》類課程而言，更是受限于計算機學科的基本特點以及高度抽象、晦澀的課程教學內容，要有針對性地開展“課程思政”，實施起來難度更大和更富有挑戰性。

中華民族是一個具有深邃智慧的民族，在漫長的歷史發展過程中，積淀了豐厚的文化和科技土壤，諸多精華觀點和思想認識具有穿透時空的生命力與前瞻性，即使在計算機信息技術和數字人工智能高度發達的今天，也毫不遜色。如吳文俊院士在中算學思想基礎上，跟現代計算機技術和原理相結合，在幾何定理自動證明和數學機械化研究方面所取得的相關成果就很說明問題［1］。實際上，在《數字信號處理》教學內容和諸多知識點中，也隱含與中算學有關的內容，從中可以挖掘出與本課程有關的思政元素，以便思政教學的實施。本文作者經過仔細的思考和分析，發現可以在“圍線積分法”求z反變換教學過程中以例題的形式把跟賈憲三角形性質有關的思政元素融入進去，對增加課程教學的知識性和趣味性，提高學生的民族自豪感和科技人文相關的綜合素養極有幫助。

本文對在“圍線積分法”求z反變換教學過程中如何有效融入思政元素進行了研究和探索。論文首先從中算學著名的賈憲三角形及其所隱含的斐波那契序列相關的代數學規律出發，介紹了該序列通項計算表達式的具體特點。然后，基于數字信號處理課程教學中z反變換求取的“圍線積分法”法，以例題形式分析了跟斐波那契序列通項公式求取相關的z變換表達式及收斂域的對應關系。在教學中，以例題講解的形式可巧妙地把相關思政元素融入進去。經過3個學期的教學實踐和反饋表明，如此進行思政教學，既可增強“圍線積分法”求z反變換教學的趣味性，又可提高學生的學習興趣和動力，具有良好的教學成效，值得在計算機學科相關教學過程中予以參考和借鑒。

2 賈憲三角形與斐波那契序列及其性質簡介

我國南宋數學家楊輝在公元1261年所著的《詳解九章算法》一書中提出了如圖1（a）所示代數三角形，很多人稱之為“楊輝三角”。在上述著作中，楊輝首先介紹了表中除“一”之外的每一個數都等于其肩上兩個數之和的遞推規律，然后專門注明“出釋鎖算書，賈憲用此術”，強調指出該方法源出于《釋鎖》一書所載算術并且已經被北宋數學家賈憲（公元1023—1050年）使用過。因此，更準確地來說，該三角應被稱為賈憲三角［2］。另外，如圖1（b）相關數碼分布規律在歐洲由法國數學家帕斯卡（1623—1662年）首先發現，故有些書上也常被稱為帕斯卡三角，但已經比賈憲三角的使用晚了500年左右。元初朱世杰把賈憲三角由七層推廣到九層，為高階等差級數求和高次招差法的發展，提供了有力的數學工具［3］。因此，賈憲三角的發現，對宋元時期中算學的發展有肇基之功，也是對世界數學發展的杰出貢獻，值得每一個中國人自豪。

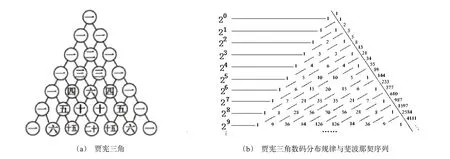
圖1 賈憲三角和斐波那契序列

賈憲三角隱含諸多有意思的代數學性質，比如它每一行數字和皆對應2 的整數次冪，而逐行冪次加1，而其斜線上數字和逐層可對應形成著名的斐波那契序列（Fibonacci sequence）即1，1，2，3，5，8，13，21，34，…，如圖1（b））所示。

斐波那契序列由大利數學家萊昂納多·斐波那契（Leonardo Fibonacci）于1202 年在《算盤書》中基于兔子問題得到［4］。其中，他給出的問題如下：“如果每對大兔每月能生育一對小兔，而每對小兔經過兩個月后才能長成大兔，那么由一對小兔開始，一年后可繁殖成多少對兔子？”。 當時斐波那契僅僅只是給出了該問題的結果，對斐波那契序列的性質并沒有作進一步的探討與分析，并且在19 世紀初以前，也沒有人認真研究過該序列。但隨著科技的發展與進步，人們發現斐波那契數列是一個非常特殊而有趣的序列，在自然科學的很多分支中都有應用，如樹木的生長、花瓣的數目、植物排列種子的“優化方式”研究、股市變化趨勢的預測等，尤其在現代物理、準晶體結構、化學和數學等領域都有直接的應用，甚至還出現在影視作品中，典型如在風靡一時的《達芬奇密碼》里它就作為一個重要的符號和情節線索出現。完全可以說，斐波那契序列是一個引起廣泛關注和社會興趣的明星序列，以致于美國數學會從 1963 年起專門出版了以《斐波納契數列季刊》為名的一份數學雜志，用于專門刊載相關的研究成果，直至今天。

實際上，斐波那契數列的每一項可基于遞推過程生成，其公式非常簡單：

而其所對應的通項公式為[5]：

需要強調指出的是，通項公式（2）與著名的黃金分割數φ直接相關，它比較有意思的特點是基于無理數整數次冪之差求出取值為整數的斐波那契序列相應數據項，并且基于該通項公式容易驗證斐波那契序列跟黃金分割數的聯系［6］

3 基于“圍線積分法”求z 反變換方式獲得斐波那契序列通項

實際上，有很多方法可以實現斐波那契序列通項的求取［7-9］。有意思的是，可以基于《數字信號處理》課程中“圍線積分法”求z反變換的方式來實現通項公式的求取和收斂域的判定，可以通過一個如下例題的求解來實現，即：已知F（z）=z/（z2-z-1），求其z反變換。

基于“圍線積分法”實現該例題的求解并不困難（具體方法請參考文獻［10］），如下給出簡單的求解步驟：

先進行F（z）的零點和極點的求取：零點為z=0，極點為z1=，具體分布如圖2所示；

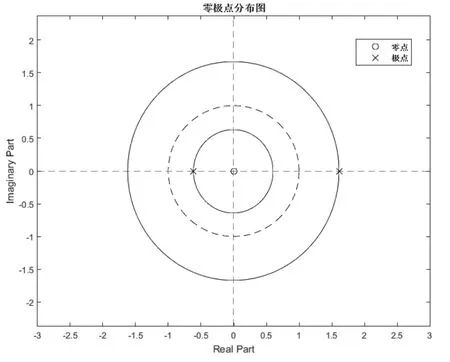
圖2 零極點分布圖

由于該表達式沒有給出具體收斂域，所以需要對其收斂域進行討論，共有三種可能的收斂域，即：

假設所對應z反變換序列為f（n），則：

（1）當|z| ＞時，f（n）首先為右邊序列，且z→ω時，F（z）=0，故f（n）應該為因果序列，故有：f（n）=0，n＜0；當n＞=0 時，zn-1F（z）=zn/（z2-2-1），在收斂域圍線內存在兩個一階極點z1和z2，可基于圍線積分法求z反變換得：f（n）=此恰為斐波那契序列之通項。此時，有F（z）=z/（z2-z-1）=

n＜=0時，zn-1F（z）=zn/（z2-z-1）分母階次比分子高2階或2 階以上且圍線外有一個一階極點z1，根據圍線積分法得：f（n）=-

當n＞0 時，zn-1F（z）=zn/（z2-z-1）在收斂域圍線內存在一個一階極點z2，可基于圍線積分法求z反變換得：f（n）=-

（3）當|z|＜時，f（n）為左邊序列：

當n＞=0 時，zn-1F（z）=zn/（z2-z-1）在收斂域內無極點，故f（n）=0，當n＜0時，zn-1F（z）=zn/（z2-z-1）分母階次比分子高2階以上且在收斂域圍線外有兩個一階極點z1和z2，基于圍線積分求z反變換得：

f（n）=-恰斐波那契序列每一項相反數。

綜上所述，基于“圍線積分法”求z反變換方法，該例題在第（1）種情況即收斂域|z|＞時不但可以把斐波那契序列的通項直接計算出來，還給出了其他2種收斂域的具體情況。

4 討論與分析

因φ=，則對于第2部分中所給出的F（z）=z/（z2-z-1）所對應z反變換的上述三種情況而言，無論其z反變換表達式，還是其收斂域邊界，都與黃金分割數φ直接相關。而在第（1）種情況下，當z=2 時又與常數2及其負整數冪次基于斐波那契序列各項的加權和直接相關。這與圖1（b）所示類似，實際上以級數展開式的形式進一步揭示了賈憲三角結構中所隱含2的整數次冪序列和斐波那契序列之間所存在的深刻數學關聯關系。

在具體實施“圍線積分法”求z反變換相關思政教學過程中，可在介紹完基于圍線積分法求取z反變換的基本方法和原理后，先將本部分中所給出的例題按正常求取步驟完成求解，隨后在分析最后結果時自然而然引出其中所關聯的黃金分割數和斐波那契序列，并順勢補充介紹一下黃金分割律在生命、科學、人文等社會各領域所存在的一些具體體現，讓學生基本了解黃金分割律的特殊性和普適性，以此吸引他們的注意力并增強課堂學習的知識性和趣味性。最后，基于第1 部分關于斐波那契序列的由來、黃金分割律的性質及其跟賈憲三角形關系相關的歷史和背景知識進行鋪墊基礎上，使得學生在獲得相關數學知識點的同時，基于對賈憲三角形相關中國古算學成就及其跟黃金分割律的聯系的了解在不知不覺中樹立民族自豪感，并對“圍線積分法”求z反變換原理和方法附帶產生濃厚的學習興趣和深入把握的沖動，從而能夠更能有動機和動力通過自主學習實現對相關知識點的掌握，最終有效改善對示例和相關知識點學習的效果，這對課程學習效率的提高以及進一步增加對本課程整個知識體系學習的興趣無疑也有幫助。

5 結論

黃金分割作為數學上的一種比例關系，具有嚴格的比例性、藝術性、和諧性，蘊藏著豐富的美學價值，它在建筑、雕塑、音樂、繪畫、運籌學、經濟分析等諸多領域有著廣泛的應用。同時，黃金分割也是一種生命科學現象和生物數學規律。具有科技和人文相交融的特點和優勢。斐波那契序列跟黃金分割律關系密切，關于其通項公式的求取，存在多種不同的數學方法。本論文結合數字信號處理課程的相關知識，以斐波那契序列通項公式的獲取方法為切入點，給出了“圍線積分法”求取z反變換方法的具體示例，不但可以增加課程教學的知識性和趣味性，同時也有助于學生在學習時能夠有效開拓視野和思路，培養多基于學科交叉融合實現守正創新的科學研究理念和素養。經過3 個學期的教學實踐和反饋表明，如此進行思政教學，具有良好的教學成效，值得在計算機學科相關教學過程中予以參考和借鑒。

致謝感謝上海理工大學健康科學與工程學院醫學影像工程研究所各位老師給本文提出的參考意見.