基于二階錐規劃的無功補償器選址定容策略

商立群,郝天奇,李 釗,鄧力文,李朝彪

(西安科技大學電氣與控制工程學院, 陜西西安 710054)

以能源綠色低碳發展為關鍵,堅持走生態優先、綠色低碳的發展道路,是中國應對氣候變化的新理念。在此大環境下以風能和太陽能為首的可再生能源技術得到快速發展。隨著分布式電源(distribution generation,DG)在配電系統中的接入比例持續增加,其出力的隨機性和波動性容易造成電壓越限、網損過高等問題,極大增加了配電網運行狀態預測的難度[1-2]。

在配電網日常運行過程中一般需要投切電容器組(capacitors banks,CB)用于提高功率因數,然而在運行期間需求和無功消耗并不是恒定或是離散的,單靠電容器組并不能完全滿足配電系統安全運行的需求。隨著電力電子器件的快速發展,靜止同步補償器(static synchronous compenstaor,STATCOM)、靜止無功發生器(static VAR generator,SVG)、靜止無功補償器(static VAR compensator,SVC)等器件相繼出現。這些電力電子器件可以作為動態無功補償裝置配合電容器組應用于配電網系統,不僅可以改善負載功率因數和電壓分布,還可以增加功率傳輸容量、控制功率震蕩和提高配電系統穩定性。因此有效的動態無功補償裝置選址和容量設置對于配電系統的安全運行具有重大意義[3-5]。

近年來,針對無功補償裝置選址不準確和容量設置困難等問題,國內外學者進行了大量的研究實驗。文獻[6]建立以網損最小、裕度最優的多目標函數優化模型,利用精英策略的自適應遺傳算法求解模型,考慮了在低壓配電網絡N-1故障情況下的無功補償裝置選址問題。文獻[7-11]建立了動態無功補償裝置的選址優化模型,分別利用Chu-Beasley遺傳算法、基于差分進化的算法、粒子群算法、灰狼優化算法、人工蜂群算法等進行求解。盡管這些方法可以找到很好的求解結果,但是建立的模型求解時間過長,模型參數選擇困難。文獻[12]通過各節點電壓對動態無功補償裝置接入的靈敏程度來選擇最佳的接入位置。文獻[13]根據節點注入功率空間中電壓穩定極限曲面的法向量確定補償器的接入位置,但二者皆只考慮了補償裝置的接入位置,沒有考慮補償器的容量設置。文獻[14]提出了應用混合整數二階錐解決無功補償裝置的選址和定容問題,但是設置目標函數單一,僅在配電網基礎結構上進行結果驗證,并沒有考慮配電系統中其他補償裝置(電容器組等)對容量設置的影響,不具有普遍性。

針對上述研究存在模型求解時間長、參數選擇困難和考慮問題不全面等問題,本文提出了基于混合整數二階錐規劃的配電網動態無功補償裝置選址和定容策略。考慮到電容器組日投切次數限制和實際配電系統中動態無功補償裝置的應用情況,選擇研究的主要對象為靜止無功補償器。該策略首先以配電系統中優化周期內的有功功率損耗最小和節點電壓偏差值最少為目標函數建立MINLP模型,在MINLP模型中求解SVC選址和定容問題的同時對配電系統中的電容器組等其他裝置投切計劃進行優化,避免對SVC容量設置的求解產生偏差。其次通過兩步松弛法(電壓電流相角松弛和二階錐松弛)將原來復雜的MINLP模型轉化為MISOCP模型,并通過ε-松弛法將MISOCP模型轉化為MILP模型,調用求解器求解。最后在IEEE 33節點和IEEE 69節點配電系統中進行測試,與使用求解器求解MISOCP模型和采用PSO算法、SA-PSO算法直接求解MINLP模型進行對比,驗證提出策略的求解時間更短、有功功率損耗更低和電壓偏差程度更小。

1 SVC選址定容模型

1.1 多目標函數

1.1.1 目標1:配電網網絡損耗最小

配電網在日常運行過程中,通過潮流計算可得到每段支路電流,從而計算出配電網的線路損耗。本文將配電網在一天24個時間段內的線路損耗作為第1個目標函數:

(1)

式中:Rij為節點i,j之間阻抗實部;T為優化周期的時段數;Δt為2個時段的時間間隔;Iij,t為t時刻線路ij之間的電流值。

1.1.2 目標2:節點電壓偏差最小

配電網在運行過程期間,在保證運行安全的前提下要盡可能減少節點電壓偏差。因此本文在保證滿足負荷需求的情況下,將配電網的節點電壓偏差最小作為目標函數:

(2)

式中:N為配電網節點數;Vi,t為t時刻節點i電壓值;VN為節點電壓參考值。

本文主要綜合考慮配電網網絡損耗與配電網節點電壓偏差這2個因素,整合后的目標函數可以表示為

F=min(f1+f2)。

(3)

1.2 約束條件

1.2.1 潮流方程約束條件

配電網日常運行中涉及的潮流方程約束條件主要包括:線路的歐姆定律、支路首端功率、節點功率平衡等,其方程可以分別表示為

Vi,t-Vj,t=ZijIij,t,ij∈B,t∈T,

(4)

(5)

(6)

式中:Vi,t和Vj,t分別表示t時間節點i,j的電壓;Zij表示節點i,j之間支路阻抗;Iij,t表示t時間節點i,j之間的電流;Sij,t表示t時間節點i到節點j的功率;Sjk,t表示t時間節點j流出的功率;Sj,t表示t時間除線路外節點j的注入功率。

1.2.2 節點電壓和支路電流的約束條件

節點電壓和支路電流約束條件分別滿足以下方程:

Vmin≤Vj,t≤Vmax,j∈N,t∈T,

(7)

Iij,t≤Imax,ij∈B,t∈T,

(8)

式中:Vmax和Vmin為電壓幅值的最大值和最小值;Imax為線路電流幅值的最大值;B為配電網中支路的集合;N為配電網中節點的集合。

1.2.3 電容器組和有載調壓變壓器運行約束條件

電容器組(CB)和有載調壓變壓器(on-load tap changer, OLTC)在配電網運行過程中為離散型決策變量,電容器組在電網中主要起到對容性負載的補償作用,而有載調壓變壓器在電網中使變電站母線節點電壓轉換成可調變量,改善節點電壓的波動問題。在配電網的日常運行周期內有嚴格的投切、調壓次數限制,所以CB和OLTC的運行約束條件分別滿足以下方程:

(9)

(10)

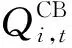
1.2.4 SVC和儲能系統的約束條件

SVC和儲能系統(energy storage system , ESS)在配電網運行中屬于連續性決策變量。SVC在電網中主要作用為抑制由于分布電源出力波動性和不穩定性造成的節點電壓波動,而ESS可靈活配置能源供應,去除高峰需求,提高電力供應質量,提供電壓和頻率保障,減少線損,提高整個輸配電系統的穩定性,由于ESS模型與電動汽車相似,因此可等效為多個電動汽車的聚類效果。SVC和ESS的約束條件分別滿足以下方程[15]:

(11)

(12)

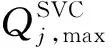
2 模型的錐轉換

2.1 二階錐規劃標準形式

本文在第一部分建立的模型中存在非凸非線性方程,若不對此進行處理,求解混合整數非凸非線性方程是十分困難的。所以需要通過二階錐規劃對其進行轉化,將方程變成混合整數凸規劃方程,應用CPLEX求解器直接對模型進行快速求解。

二階錐規劃是凸優化問題的一種特例,是一種高效處理非線性優化問題的求解方法。很多復雜的優化模型問題都可以通過二階錐規劃轉換成二階錐優化模型進行求解,在保證求解精度的前提下,很大程度上減少模型求解難度,縮短模型求解計算時間。其標準形式如下所示:

(13)

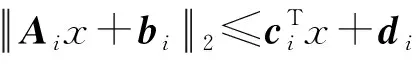
2.2 模型的二階錐轉化

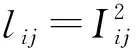
目標函數:

約束條件:

(14)

但是在約束條件(14)中第4個方程仍為一個非凸非線性方程,所以采取二階錐松弛的方法使其變成二階錐約束方程,轉換后的方程可表示為

(15)

其等效形式可表示為

(16)

因此,不等式(15)可以轉換為標準的二階錐公式,經過等效變換之后可以用不等式(16)代替約束條件式(14)中的第4個等式。至此,MINIP模型成功轉化成為MISOCP模型。根據Ben-Tal and Nemirovski 提出的“ε-松弛”方法[16],使用多面體近似描述二階錐,將求解MISOCP模型問題轉化為求解MINLP模型,可以表示為

(17)

(18)

式中:m=0,1,…,k,通過化簡去掉變量am和所有等式約束,將二階錐不等式約束轉化為線性不等式約束,達到將MISOCP模型轉化為MINLP模型的目的。其中松弛變量ε可表示為

(19)

本文中k取10,ε=6×10-7[17],ε越小,二階錐多面體程度越高,精確度越高。對于本文所提及的松弛法,簡單來說是一種在不影響模型求解結果的前提下,將非凸集合放大成凸集合并縮小求解范圍的方法,文獻[18—20]也證明了對于大部分配電網結構而言,松弛過后所得到的解是嚴格準確的。至此原來的復雜優化模型求解問題已經轉化成為二階錐規劃問題,直接調用商業求解器求解即可,本文使用的求解器為CPLEX12.90。

3 算例仿真及分析

3.1 算例介紹

本文采用IEEE 33節點和69節點的配電系統以一天24個時間段為一個優化周期進行算例分析,配電系統電壓基準值為12.66 kV,功率基準值為10 MW,其基礎結構如圖1所示。

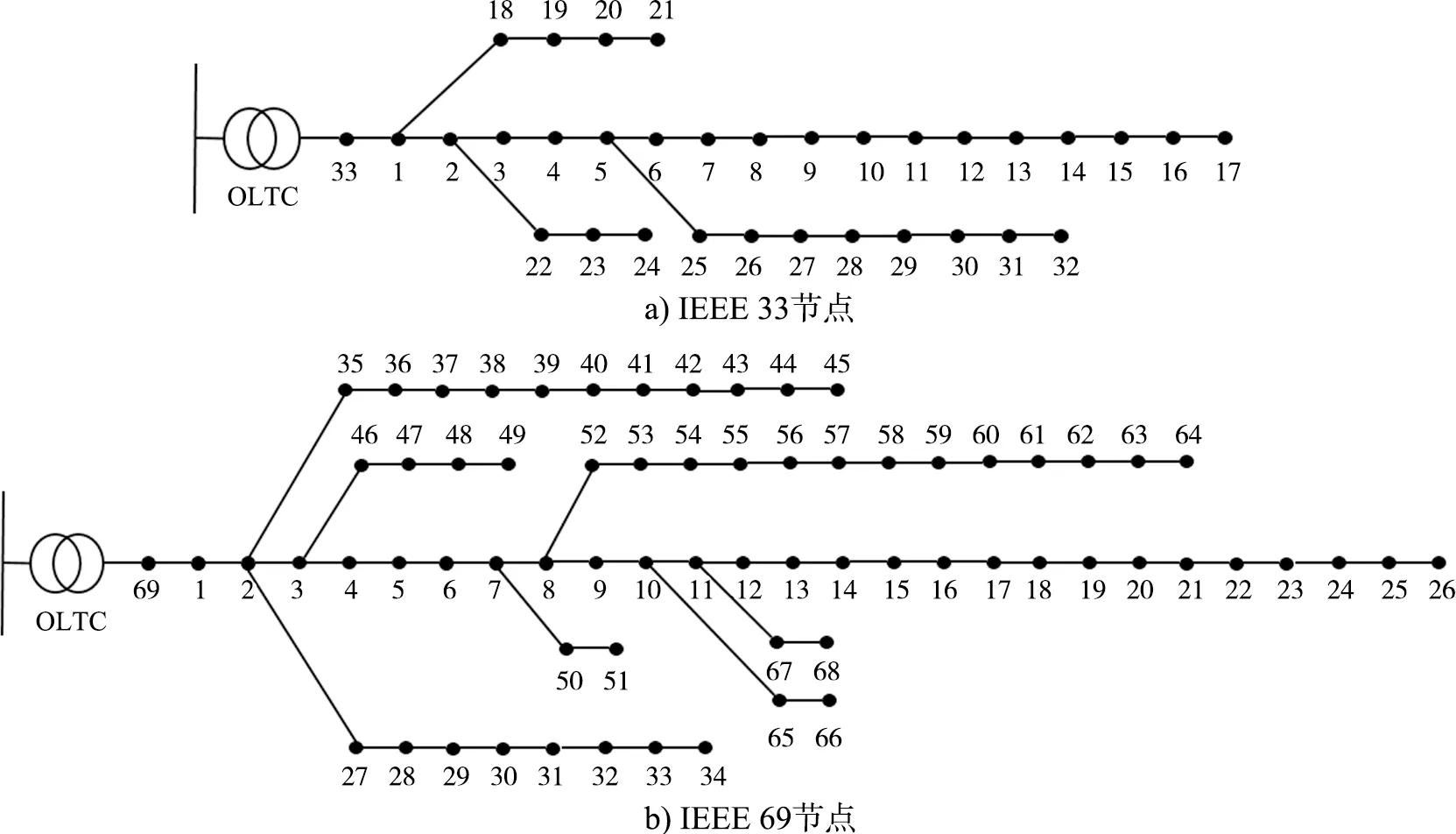
圖1 配電網系統 Fig.1 Network system

在本文2個算例系統中標準負荷設置為(3.815+j2.7)MW,考慮到在一天周期之內負荷會隨時間變化而變化,所以在本文中假設配電系統中的負荷變化如圖2所示,單個時間段內的最大負荷為(3.79+j2.484)MW。分布式電源出力曲線如圖3所示。

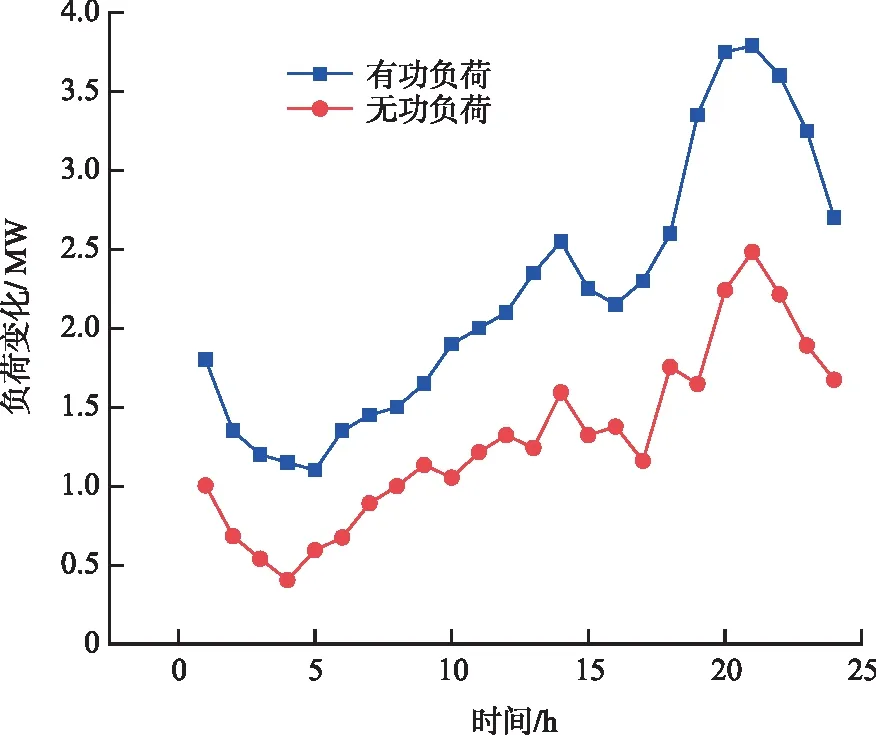
圖2 負荷變化曲線Fig.2 Load curve in a day

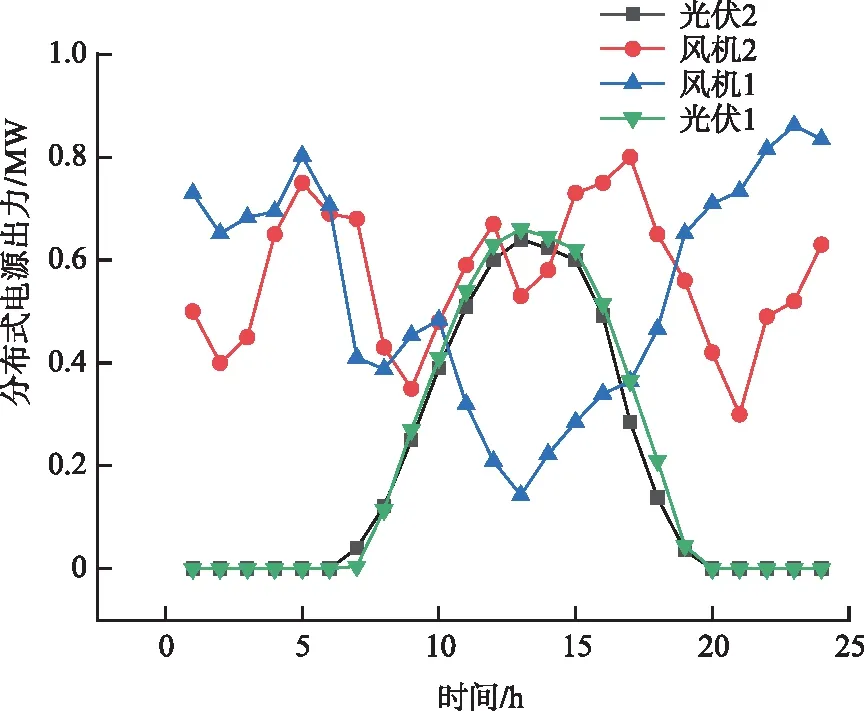
圖3 分布式電源出力曲線Fig.3 Distribution generation output curve in a day

風機1、風機2和光伏1、光伏2分別處于69節點配電系統中26,31,45,63節點。風機1和光伏1同時處于33節點系統中的17,32節點。OLTC電壓變比檔位上限為12檔,變比調節范圍為[0.94,1.06],一天優化周期內調節次數上限為5次。SVC的無功補償裝置數量為3個。ESS和CB裝置的參數見表1、表2。

表1 儲能系統參數Tab.1 Parameters of energy storage system

表2 電容器組參數Tab.2 Parameters of capacitors banks

3.2 優化結果分析

本文的所有實驗程序皆是在Matlab R2020a環境下基于CPLEX12.9.0求解器進行計算的,系統硬件環境為i5-1135G7 CPU 2.40 GHz,16 GB內存,操作系統為Win10 64 bit.

應用本文提出的方法在給出的33節點和69節點配電網系統中進行結果驗證,得到SVC最佳選址位置和容量設置,并用bonmin求解器、PSO優化算法和SA-PSO算法分別直接求解MINIP模型和CPLEX求解MISOCP模型進行對比實驗,驗證本文方法的優越性。本文中假設網損成本為5 000＄/(MW·h)。最終的對比實驗結果如表3、表4所示。

表3 不同方法在33節點配電系統求解信息結果的對比Tab.3 Comparison of different methods for solving information and result in 33-bus network

表4 不同方法在69節點配電系統求解信息結果的對比Tab.4 Comparison of different methods for solving information and result in 69-bus network

從表3、表4可以看出,使用CPLEX求解器求解MILP模型相比于求解MISOCP模型和SA-PSO優化算法和PSO直接求解MINIP模型計算時間分別縮小1.2,2.5和3 min左右,說明通過ε-松弛后的模型更易求解。而在求解結果方面,在33節點配電系統優化周期內網損成本分別縮小了27.55,91.6和93.48＄,電壓偏差標幺值分別縮小了0.002 4,0.005 2和0.007 3 pu。在69節點配電系統優化周期內網損成本分別縮小了22.6,44.13和128.4＄,電壓偏差標幺值分別縮小了0.001 2,0.009 1和0.010 5 pu,說明通過松弛過后的模型仍能保證全局最優解。而應用Bonmin求解器直接求解本文中建立的MINIP模型并沒有成功求得模型的解。

本文在進行SVC選址定容實驗的同時對配電系統中的其他裝置進行投切優化,尤其是CB投切情況會直接影響SVC容量的求解結果。應用本文提出的方法在2個配電系統中優化得到的CB出力情況和SVC動態補償結果如圖4-圖7所示,可知CB裝置的投切轉換次數和SVC裝置的無功投入量皆滿足約束條件,符合模型求解要求。

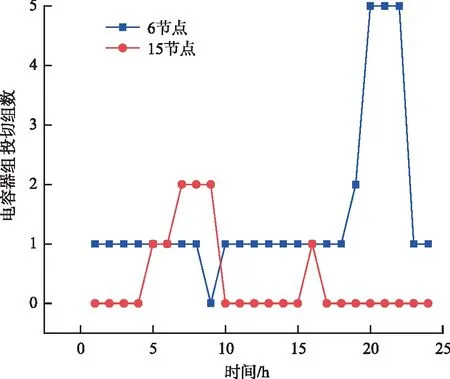
圖4 33節點系統CB出力計劃Fig.4 CB output plan for a day in 33-bus network

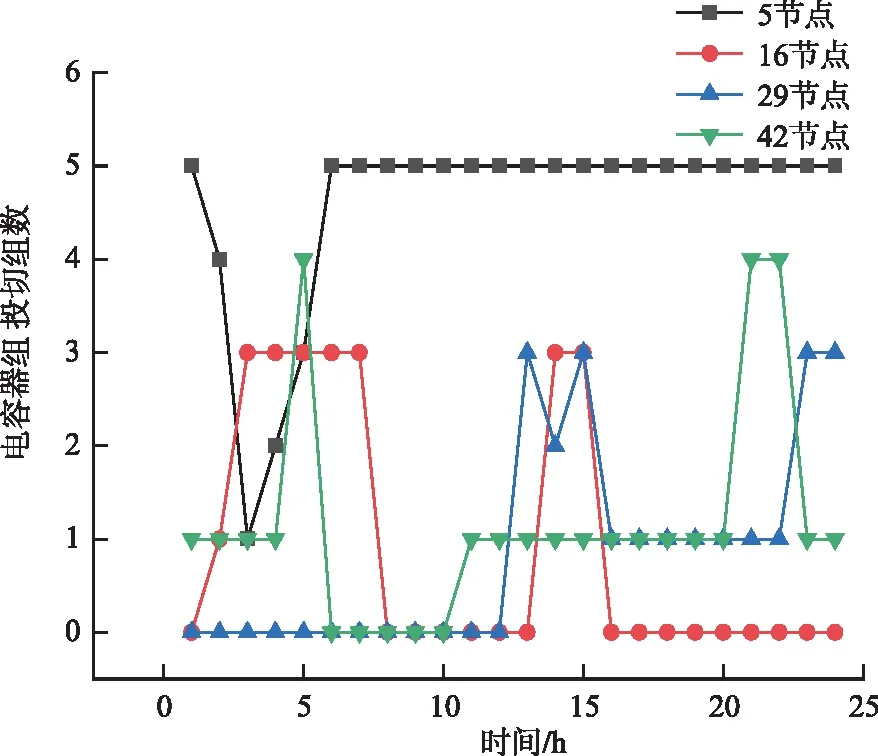
圖5 69節點系統CB出力計劃Fig.5 CB output plan for a day in 69-bus network

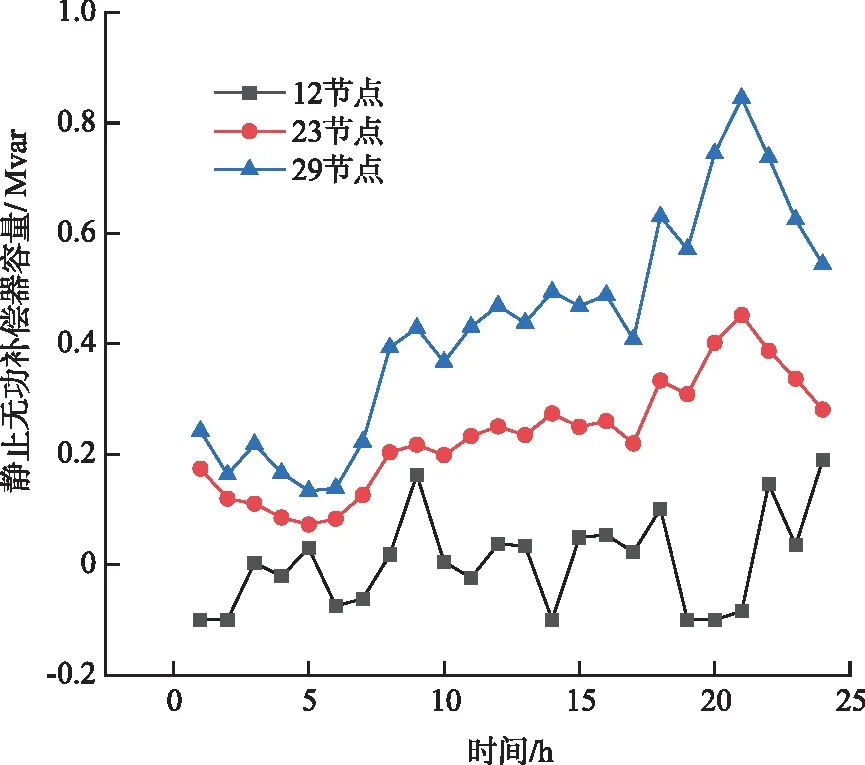
圖6 33節點系統靜止無功補償器出力計劃Fig.6 Static var compensator output plan for a day in 33-bus network

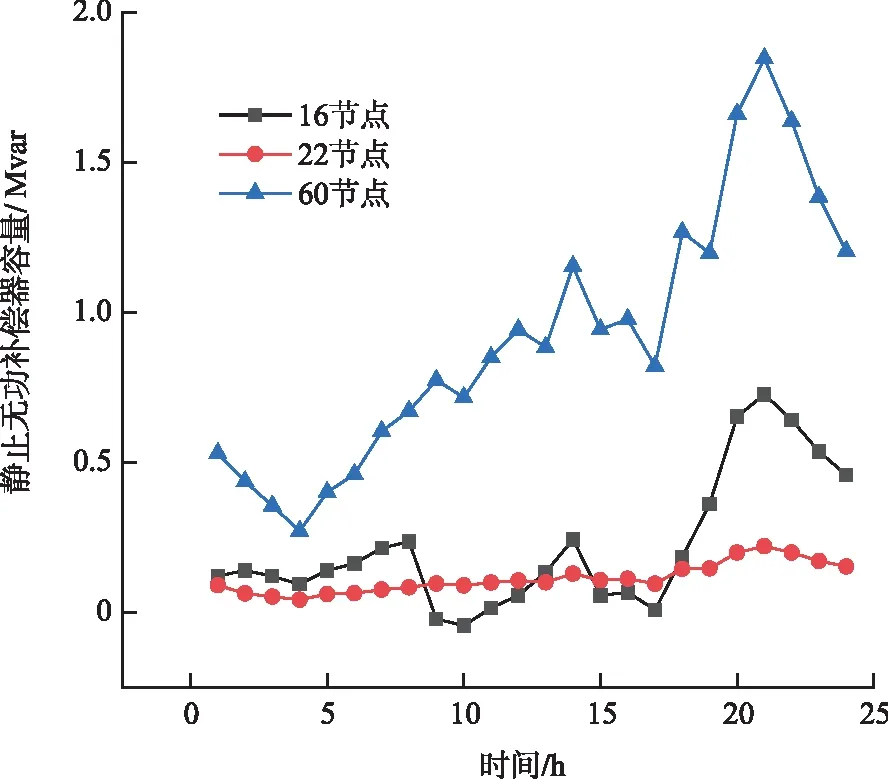
圖7 69節點系統靜止無功補償器出力計劃Fig.7 Static var compensator output plan for a day in 69-bus network

4 結 論

隨著分布式電源在城市配電網絡中滲透率的提高,DG在提供清潔能源的同時,也對配電系統中動態無功補償裝置的選址定容提出更高的要求。本文以SVC為主要研究對象,提出了基于混合整數二階錐規劃的配電網動態無功補償選址和定容策略,考慮了其他無功補償裝置對SVC接入的影響,結合實際IEEE 33節點和IEEE 69節點配電系統進行算例測試,可得出以下結論。

1)相比于傳統選址定容方法,本文提出的方法利用相角松弛和二階錐松弛的方法將原來復雜的MINIP模型轉化成為符合凸優化條件的MISOCP模型,并用ε-松弛將MISOCP模型轉化為MILP模型,最后調用CPLEX12.90求解器求解,既能簡化模型復雜程度,又保證了全局最優解,同時減少了模型求解時間。

2)所提出的方法考慮了CB接入對SVC的影響,在求解SVC選址定容問題的同時優化配電系統中CB的投切情況,能夠得到更符合真實情況的SVC容量設置、網絡損耗量和節點電壓偏差值,更具有真實性和普遍性。

本文所提的SVC選址定容策略僅考慮了電容器組的無功輸出情況,下一步將針對發電機等其他無功補償裝置接入配電網進行研究,以更好地滿足選址定容要求。