超臨界CO2熱泵蛇形管氣冷器傳熱特性研究

崔海亭,王 超,王 晨

(河北科技大學機械工程學院,河北石家莊 050018)

在“碳達峰、碳中和”的目標背景下,節能減排是一項重要舉措。在制冷行業,傳統的CHCs和HCHCs類制冷劑仍會產生溫室氣體,使臭氧層遭受破壞。因此,尋找節能環保的制冷劑對目標的實現意義重大[1-2]。CO2作為一種自然工質,因其具有無毒、不燃、安全、成本低、環境友好等特點[3],引起了制冷、熱泵等領域的研究人員和工業界的關注。氣體冷卻器作為CO2熱泵系統中的關鍵部件,決定著整個系統的運行效率,超臨界CO2在氣冷器中放熱有著較大的溫度滑移,可以將冷卻水加熱至較高的溫度。最近有研究表明,CO2跨臨界系統有著較高的節能潛力[4-8]。然而,由于CO2在臨界點處急劇變化的物理性質,超臨界壓力下CO2換熱比跨臨界壓力下換熱機理更為復雜,因此有必要深入研究超臨界CO2在換熱管中的換熱特性。

超臨界CO2在管內的流動和傳熱過程受到廣大學者的廣泛研究[9-12],主要是超臨界CO2在直管和螺旋管流動的研究。由于在臨界點處CO2密度發生突變,產生浮升力和流動加速效應,從而對超臨界CO2的流動換熱產生影響。當CO2在管內流動時,不同的操作參數會對管內工質的傳熱特性產生影響。顧騫[13]對不同操作參數下超臨界CO2在直管和螺旋管的對流傳熱過程進行了數值模擬,模擬結果表明在直管中,擬臨界點處浮升力對傳熱的影響不可忽略,增大入口雷諾數會強化換熱,增大管內壓力會使傳熱系數峰值減小;在螺旋管中,浮升力的影響在流體達到臨界點前不可忽略。白萬金等[14]對不同操作參數下超臨界CO2在水平直管的流動傳熱進行實驗研究,結果表明質量流速越大,傳熱系數越大;壓力越大,傳熱系數峰值點所處的溫度越高。崔海亭等[15]通過數值模擬對不同操作參數下超臨界CO2在直管套管內的熵產進行了計算,結果表明壓力和熵產成正比,質量流量和熵產成反比。

目前,對超臨界CO2在蛇形管[16-18]內流動換熱的研究比較有限。羅峰等[19]對超臨界CO2在微細蛇形管內層流對流換熱系數的影響進行了研究,對比分析了微細蛇形管豎直和水平對CO2流動換熱的影響,結果表明,當重力和入口流動方向相反時,截面處溫度和速度對稱分布,否則對稱分布效果減弱。黃騰等[20]對不同結構蛇形管內的超臨界CO2進行了數值模擬,結果表明曲率直徑或內徑的增加均會降低傳熱系數。對于超臨界CO2對蛇形管傳熱的影響的研究多針對結構參數,而對不同操作參數下的蛇形管換熱研究較少。

本文針對套管式蛇形管氣體冷卻器建立物理模型,通過改變操作參數對管內超臨界CO2的流動和換熱特性進行研究,具體分析不同壓力、不同質量流量下超臨界CO2的傳熱性能。

1 模型與求解

1.1 物理模型

蛇形管結構示意圖如圖1所示,該氣體冷卻器采用套管式。蛇形管管長L=1 200 mm,曲率直徑D=109.20 mm,外管內徑d1=14 mm,材料為不銹鋼,內管為管徑d2=3.80 mm、壁厚δ=1.1 mm的不銹鋼管。物理模型由3部分區域組成:CO2流動區域、內管壁厚區域、冷卻水流動區域。氣冷器內管工質為CO2流體,內管和外管的空腔為冷卻水,在本文中二者呈逆流換熱。為了簡化模型,作出如下假設:

圖1 蛇形管氣冷器物理模型Fig.1 Physical model of serpentine tube air cooler

1)假設模型為絕熱系統,不與外界進行能量交換;

2)忽略套管外管壁厚的影響。

1.2 邊界條件與網格劃分

本文模擬采用壓力求解器,壓力-速度耦合采用SIMPLEC算法,壓力插值格式為PRESTIO!,動量、能量、湍動能等采用二階快速QUICK格式,設置收斂殘差為10-6,當滿足殘差要求且進出口流量守恒時,計算完成。管內介質為超臨界CO2,物性參數通過REFPROP獲得,在Fluent軟件中通過piecewise-liner輸入變物性數據,節點數取8個。采用RNGk-ε模型和增強壁面函數,冷卻水和CO2入口均為質量流量入口,出口為壓力出口,外管外壁面設為絕熱,內管內壁和外壁設為流固耦合壁面,邊界條件具體參數如表1所示。

表1 蛇形管氣冷器邊界條件設置Tab.1 Setting of boundary conditions of serpentine tube air cooler

蛇形管網格劃分使用Gambit軟件,網格類型為結構化網格,近壁處由于流體受邊界層存在的影響,會對溫度等特性產生影響,故在內管內壁和外壁與流體交界處劃分邊界層,從而加強計算的準確性。本模型網格質量評價指標Equisize Skew<0.4的網格數占總網格的99.67%,網格質量良好。蛇形管網格劃分示意圖如圖2所示。

圖2 蛇形管網格劃分示意圖Fig.2 Schematic diagram of serpentine tube meshing

1.3 數學模型

本文采用RNGk-ε模型進行計算,數學模型包括連續性方程、動量方程、能量方程、湍動能方程(k方程)和耗散率方程(ε方程),具體公式如下。

連續性方程:

(1)

動量方程:

(2)

能量方程:

(3)

湍動能方程:

(4)

耗散率方程:

(5)

式中湍流黏度μt定義如下:

(6)

1.4 數據處理

為了更好地看出內管CO2的流動狀態,設置了重力g,其方向與Z軸正方向一致,且模擬過程所有的參數均選用國際單位。

蛇形管橫截面上的主流溫度Tf取質量加權平均溫度,公式如下:

(7)

超臨界CO2在管內流動的局部傳熱系數hi和平均傳熱系數h為

(8)

(9)

式中:u,ρ,Cp,qw,Tw,i和Tf,i分別表示速度、流體密度、定壓比熱容、熱流密度、局部壁溫、截面主流溫度。

2 模型驗證

網格無關性驗證數值模擬驗證結果如圖3所示。在CO2和冷卻水的質量流量分別為0.004和0.030 kg/s,CO2壓力為8 MPa的工況下,對模型進行網格無關性驗證。圖3 a)展示了網格數分別在465 124,1 411 766和3 192 000下,沿管長方向CO2主流溫度的變化。由圖3 a)可以看出,CO2出口溫度分別為306.96,305.75和305.69 K,網格數為1 411 766和3 192 000時,CO2出口溫度基本不變,且曲線基本保持一致。為加快計算速度和保證計算精度,選取網格數為141 766進行數值模擬。

圖3 無關性驗證和數值模型驗證Fig.3 Verification of independence and validation of numerical models

為驗證數值模型和計算方法的準確性,采用文獻[21]中的實驗條件,用等比例方法建立物理模型。參考文獻中蛇形管內徑為0.953 mm,外徑為2.1 mm,管長L為88 mm;文獻中對蛇形管進行加熱,故模擬時設置恒熱流壁面條件。以CO2壓力為7.65 MPa,CO2質量流量為1 kg/h,壁面熱流為50 kW/m2工況為例進行數值模型驗證。圖3 b)為沿管長方向CO2主流溫度和壁面溫度變化情況,由圖3 b)可以看出,模擬值和實驗值變化趨勢基本一致,且CO2主流溫度模擬值較實驗值平均誤差為0.69%,壁面溫度模擬值較實驗值平均誤差為1.59%,誤差均在允許范圍內。因此,本數值模型具有可靠性。

3 結果與分析

本文采用Fluent軟件對蛇形管進行仿真模擬,由于超臨界CO2物性參數在臨界點附近變化較大,故本文只對內管即CO2流動區域進行分析討論。冷卻水入口溫度為290.15 K,CO2入口溫度為333.15 K。

3.1 蛇形管內部流動特性分析

圖4和圖5分別為CO2入口質量流量為0.004 kg/s,入口壓力為8 MPa,冷卻水入口質量流量為0.03 kg/s時,在不同截面處的速度云圖和溫度云圖。由圖4、圖5可知,CO2沿著流動方向受到二次流的影響,不同截面處的速度云圖和溫度云圖發生了明顯的變化。最初CO2在云圖上呈現一對渦流,且在2L/7處之前云圖呈現中間向兩側擴散的趨勢,這表明在入口處由于主流體和壁面溫差較大,在重力和離心力的作用下,使得湍流程度較大;沿管長方向,渦流數量逐漸減小,湍流程度減弱,且云圖呈現由內側向外側和由外側向內側交替擴散的趨勢,從截面流動方向也能看出這種變化,這是由于蛇形管的結構所致,蛇形管周期性的彎曲反向使得離心力也周期反向,在離心力和重力的作用下,CO2向密度較小的一側擴散。由速度云圖可知,沿著管長方向CO2流速逐漸降低,且流速在入口處變化較大,之后變化較小,在2L/7處較L/7處減小了0.24 m/s,在5L/7處較4L/7處減小了0.17 m/s。由溫度云圖可知,沿著管長方向CO2主流溫度逐漸降低,且溫度呈現先快速下降再緩慢下降的趨勢,入口處由于溫差較大,溫度下降較快,到x=L/7處溫度已經從333.15 K降低到321.63 K,此時溫度已經降低了3.46%;在x=3L/7之后由于溫差和湍流強度的減小,導致截面處二次流減弱,因此截面處溫度云圖變化不再顯著。

圖4 蛇形管不同截面速度云圖和流線圖Fig.4 Cloud and streamline diagrams of velocity on different sections of serpentine tube

圖5 蛇形管不同截面溫度云圖Fig.5 Cloud chart of temperature on different sections of serpentine tube

圖6為沿管長方向湍動能的變化。由圖6可知,湍動能在入口附近先增大再減小,這是因為在入口附近溫差較大,同時由于蛇形管連續彎曲的結構導致離心力周期反向,從而湍流程度增大。由此可得,蛇形管周期性的彎曲反向使得離心力也周期反向,從而云圖呈現周期性的內側和外側交互擴散的趨勢,強化了換熱效果。

圖6 沿管長方向湍動能的變化Fig.6 Changes in turbulent kinetic energy along a rectangular tube

3.2 CO2壓力對傳熱特性的影響

為考察CO2壓力變化對蛇形管內超臨界CO2流動換熱的影響,設置CO2入口質量流量為0.004 kg/s,冷卻水入口質量流量為0.03 kg/s,分別改變CO2入口壓力為8,9和10 MPa,對蛇形管進行傳熱模擬。CO2在不同壓力下沿管長方向主流溫度變化和傳熱系數變化如圖7和圖8所示。由圖7和圖8可以看出,不同壓力下,沿管長方向CO2主流溫度均呈下降趨勢,傳熱系數均呈先上升再下降趨勢。

圖7 不同壓力下沿管長方向主流溫度變化Fig.7 Temperature variation of the mainstream along the length direction of the pipe under different pressures

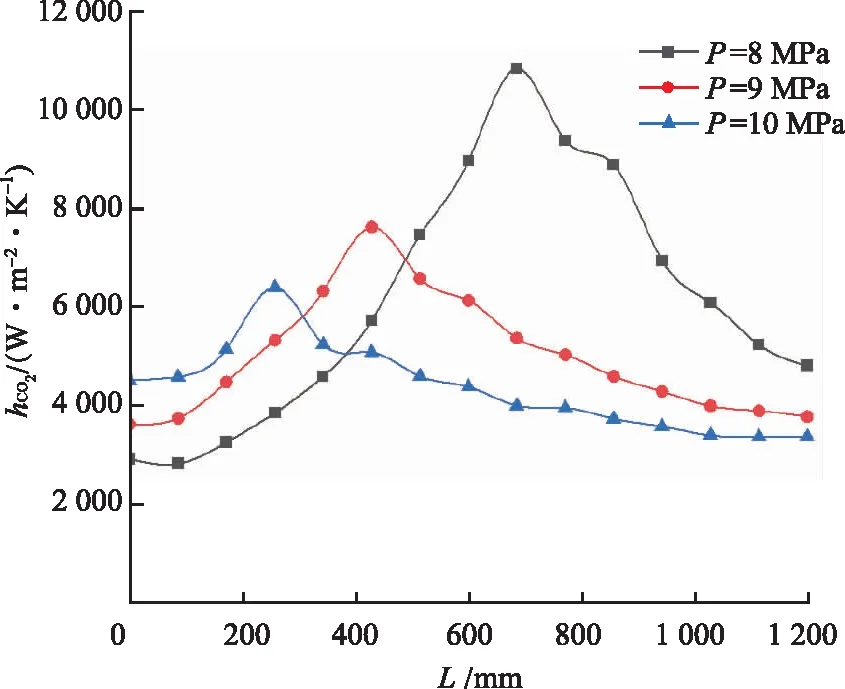
圖8 不同壓力下沿管長方向傳熱系數變化Fig.8 Change of heat transfer coefficient along the tube length under different pressures

如圖7所示,沿管長方向CO2主流溫度先快速降低再緩慢降低,壓力越低,主流溫度快速下降得越快,緩慢下降得越慢。入口處由于較大的溫差,主流溫度快速下降,壓力越接近臨界壓力,湍流動能越大,因此,低壓下主流溫度快速下降的越快,壓力越低,主流溫度緩慢下降的越慢,這可以減小和壁面之間的溫差,使得CO2充分換熱。同時,CO2進出口溫差也不同,壓力越小,進出口溫差越小。當壓力為8 MPa時,出口溫度為305.76 K,進出口溫差為26.12 K;當壓力為9 MPa時,出口溫度為304.38 K,進出口溫差為27.64 K;當壓力為10 MPa時,出口溫度為301.69 K,進出口溫差為30.50 K。因此,減小壓力可以使CO2充分換熱。

如圖8所示,在不同壓力下,沿著管長方向傳熱系數先增大,到臨界點達到峰值,隨后再減小。壓力越大,峰值越小,這是因為在臨界點處,CO2比熱容的急劇變化導致換熱系數的變化,同時壓力越高,擬臨界溫度就越高,導致到達峰值點的位置提前。不同壓力下超臨界CO2的擬臨界溫度如表2所示。

表2 不同壓力下的擬臨界溫度值Tab.2 Critical temperature values under different pressures

不同CO2溫度狀態下的傳熱系數明顯不同,在CO2溫度較高時,壓力越大,傳熱系數越高;相反,在CO2溫度較低時,壓力越大,傳熱系數越低。這是由CO2變物性所致,在臨界點之前,CO2溫度較高,隨著CO2壓力的升高,定壓比熱容和熱導率逐漸升高,在臨界點之后則相反。當P=8 MPa,時,峰值點傳熱系數為10 855.89 W/(m2·K),平均傳熱系數為6 135.89 W/(m2·K),較P=9 MPa時分別提高了63.59%和24.37%;較P=10 MPa時分別提高了98.76%和42.53%。因此,壓力越低,越靠近準臨界點,換熱系數越大,越有利于換熱。

3.3 CO2質量流量對傳熱特性的影響

為了解CO2質量流量變化對蛇形管內超臨界CO2流動換熱的影響,設置CO2入口壓力為8 MPa,冷卻水入口質量流量為0.03 kg/s,分別改變CO2入口質量流量為0.003,0.004和0.005 kg/s對蛇形管進行傳熱模擬。不同CO2質量流量下沿管長方向的溫度分布和傳熱系數變化分別如圖9和圖10所示。

圖9 不同CO2質量流量下沿管長方向溫度分布圖Fig.9 Temperature distribution along the tube length under different CO2 mass flow rates

圖10 不同CO2質量流量下沿管長方向傳熱系數變化Fig.10 Change of heat transfer coefficient along the tube length under different CO2 mass flow rates

由圖9可知,在不同質量流量下主流溫度和壁面溫度隨著管長變化而變化的趨勢基本相同,都呈下降趨勢。但CO2的進出口溫差以及CO2和壁面的溫差卻有所不同,當CO2質量流量為0.003 kg/s時,出口溫度為302.41 K,進出口溫差為29.18 K;當CO2質量流量為0.004 kg/s時,出口溫度為305.76 K,進出口溫差為26.12 K;當CO2質量流量為0.004 kg/s時,出口溫度為307.12 K,進出口溫差為24.97 K,質量流量越大,進出口溫差越小。CO2和壁面的溫差變化也是如此,在流量分別為0.003,0.004,和0.005 kg/s時,最小溫差分別為5.16,4.28和3.81 K。由此可得,隨著CO2質量流量的增加,超臨界CO2冷卻換熱具有更小的溫差,具有更小的溫度滑移,可以充分換熱。

由圖10中傳熱系數模擬值可知,不同CO2質量流量下傳熱系數的變化趨勢一致,沿管長方向先增加,在臨界點達到達峰值后再下降。這是由于CO2的變物性所致,在臨界點處比熱和熱導率最大。質量流量越低,到達峰值點的位置越靠前,這是因為低質量流量下的CO2主流溫度會較早地降低到擬臨界溫度點。CO2質量流量越大,峰值點越大,CO2質量流量為0.005 kg/s的峰值點較0.003和0.004 kg/s分別提高了54.18%和16.88%,質量流量為0.005 kg/s的平均傳熱系數較0.003和0.004 kg/s分別提高了57.92%和19.83%。由此可得,隨著CO2質量流量的增加,湍流強度加強,邊界層變薄,導致傳熱得到改善,平均傳熱系數提高。

3.4 冷卻水質量流量對傳熱特性的影響

為了解冷卻水質量流量變化對蛇形管內超臨界CO2流動換熱的影響,設置CO2入口壓力為9 MPa,質量流量為0.004 kg/s,分別改變冷卻水質量流量為0.02,0.03和0.04 kg/s對蛇形管的傳熱性進行模擬。不同冷卻水質量流量下沿管長方向傳熱系數的變化,如圖11所示。從圖11可以看出,沿管長方向不同冷卻水質量流量下的傳熱系數都是先增加后減小,在臨界點附近達到峰值,且峰值點傳熱系數相差不大。在CO2溫度較高時,冷卻水的質量流量越大,傳熱系數越高;相反,傳熱系數越低。這是由于CO2流體的變物性所致,冷卻水質量流量的變化引起CO2主流溫度的變化,從而影響CO2的定壓比熱容和熱導率。

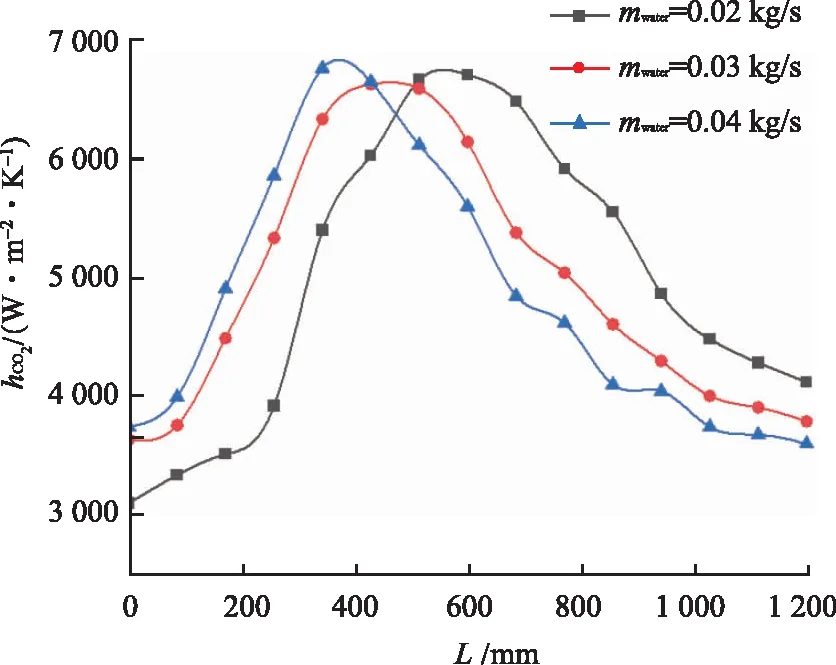
圖11 不同冷卻水質量流量下沿管長方向傳熱系數變化Fig.11 Change of heat transfer coefficient along tube length under different cooling water mass flow

冷卻水質量流量越大,到達峰值點的位置越靠前,冷卻水質量流量分別為0.02,0.03和0.04 kg/s時的平均傳熱系數分別為5 029.89,4 933.66 和4 821.84 W/(m2·K)。由此可知,冷卻水質量流量的增加不會影響傳熱系數的峰值點,但會使峰值點所在的位置提前,質量流量越大,平均傳熱系數越低。

4 結 論

1) 通過對蛇形管內部CO2流動特性分析可知,由于離心力的周期性反向,在重力的作用下,導致溫度和速度梯度呈現出內側和外側周期性交互擴散的變化趨勢,從而強化換熱。在入口處由于溫差較大,蛇形結構使得溫度和速度云圖均產生多個渦,湍流強度增大。

2) 相同工況下,CO2壓力越接近臨界點,平均傳熱系數越大,壓力為8 MPa時的平均傳熱系數較為9 MPa和10 MPa分別提高了24.37%和42.53%。由于受超臨界CO2物性參數的影響,在CO2溫度較高時,壓力越大,傳熱系數越高;相反,在CO2溫度較低時,壓力越大,傳熱系數越低。

3) 相同工況下,CO2質量流量越大,平均傳熱系數越高,這是由于隨著超臨界CO2質量流量的增加,邊界層厚度不斷減薄,湍流更加劇烈,換熱更充分。

4) 相同工況下,冷卻水質量流量越大,平均傳熱系數越低。冷卻水質量流量的增加對峰值點的傳熱系數沒有影響,但會使峰值點出現的位置提前。

本文采用數值模擬的方法對超臨界CO2在蛇形管中的冷卻過程進行了分析,通過改變操作參數,分析其換熱性能。未來需進一步研究結構參數變化對超臨界CO2在蛇形管中換熱特性的影響,以綜合評價蛇形管的傳熱性能。