低值易耗品采購預算的成本預測模型研究
——以L學院為例

武學志,詹競舟

(蘭州職業技術學院 國資及產業管理處, 甘肅蘭州730070)

黨的十八大以來,國家極為注重建設資源節約型和環境友好型社會。2021年7月,國家發展和改革委員會發布的《“十四五”循環經濟發展規劃》提出了新的目標,即到2025年,我國將基本建立資源循環型產業體系,建成全社會的資源循環利用體系,主要資源產出率比2020年提高約20%,單位國內生產總值的能源消耗和用水量比2020年分別降低13.5%和16%左右。這些明確的目標對經濟社會的可持續發展提出了更高的要求[1]。節約資源不僅是發展生產力的有效手段,同時也是有效的環境保護措施,是統籌人與自然和諧發展的重要舉措。

一、研究意義

低值易耗品是指單項價值在規定限額以下并且使用期限不滿一年、能多次使用而基本保持其實物形態的勞動資料[2]。筆者通過對近幾年L學院低值易耗品采購、使用情況的分析,發現低值易耗品的種類不斷擴大,消耗量逐年上升,造成低值易耗品采購預算隨之不斷增加。這對L學院的高水平、高質量建設和深化資源整合產生了一定的影響;同時,也未能達到資源節約型社會建設與發展的要求。在此背景下,本文通過對L學院部分有代表性的低值易耗品采購、使用數據的分析,提出一套低值易耗品采購成本的預測模型。該預測模型能夠優化和控制低值易耗品采購預算規模,節約經費開支,有效降低資源消耗,符合國家建設資源節約型社會的總體要求。

二、存在問題

低值易耗品采購預算與實際采購、使用存在以下關系:低值易耗品的采購預算一般是根據歷史數據編制,但在執行過程中,實際支出可能會高于或低于預算。

(一)低值易耗品采購預算與實際追加之間的矛盾

預算是實際采購的基礎和指導,對低值易耗品實際采購的規模和結構起著重要的引導作用。在實際使用過程中,由于低值易耗品不斷消耗滅失,在需要增補的情況下,追加預算就是一個不斷調整和完善的過程,以確保低值易耗品使用的合理性和經濟性。

(二)低值易耗品預算與實際采購、使用之間的矛盾

一方面,預算的編制是基于歷史使用數據和市場趨勢的分析,可能存在預測偏差和不確定性,導致實際使用量與預算存在一定偏差。另一方面,采購會受到多種因素的影響,如供應情況、市場變化、需求波動等,這些因素可能導致在實際使用量未發生明顯變動的情況下采購超出預算范圍。

因此,從采購源頭做好對低值易耗品采購預算的預測顯得至關重要。一是加強對預算和采購的雙向數據分析和監控,建立有效的數據采集和分析機制,隨時監測采購數據,發現問題并及時進行干預。二是對低值易耗品使用數據進行統計學分析,設計科學的預測模型,預測未來采購趨勢,以提高預算的準確性和有效性,節約經費開支。

三、研究方案

研究以L學院部分有代表性的低值易耗品的使用需求、采購規模和消耗量等數據集合作為數據分析基點,運用統計定量分析中貝葉斯方法和Python語言實現等方法,在質量和技術層面進行客觀數據解析,建立初步預測模型,并開展實證分析。

(一)貝葉斯方法

貝葉斯方法是一種基于概率論的統計推斷方法,可以用于低值易耗品需求概率推斷和預測分析。下面簡要介紹如何使用貝葉斯方法來實現這一目標。

1.確定先驗概率分布

先驗概率分布是指在沒有任何數據的情況下,對需求的概率分布的預估。先驗概率分布可以基于以往經驗或行業標準等因素來確定。

2.收集低值易耗品需求數據

這些數據包括歷史采購記錄、一年的需求量和實際使用量、使用頻率、庫存數量等。這些數據將用于計算后驗概率分布。

3.計算后驗概率分布

使用貝葉斯定理,根據先驗概率分布和收集到的數據,計算出新需求的概率分布。這個過程可以使用貝葉斯公式來實現:

P(需求|數據)=P(數據|需求)×P(需求)/P(數據)

其中,P(需求|數據)是后驗概率分布,P(數據|需求)是似然函數,P(需求)是先驗概率分布,P(數據)是歸一化常數[3]。

4.需求概率評估

在確定后驗概率分布的基礎上,對需求的概率分布進行重新估計,例如計算出需求量的期望值、方差、置信區間等,來幫助決策者制訂相關方案。

(二)建模機理

在研究過程中使用貝葉斯方法對概率分布進行建模,用所采集的一定量低值易耗品采購、使用數據更新概率分布,以確保結果的準確性。在應用貝葉斯方法進行決策分析時,需要充分考慮數據的可用性和真實質量,以及對概率分布的準確建模。

(三)建立貝葉斯隨機效應模型

1.模型構建

(1)分析數據

分析低值易耗品的采購、使用數據,包括需求量、采購量、使用量、庫存量、報廢量、成本等信息。

(2)設計先驗分布

通過對歷史數據的分析,確定每種低值易耗品的需求、采購、使用的概率分布,作為先驗分布。

(3)設計似然函數

似然函數是觀測數據在給定參數下的概率分布。根據數據的不同特點,選擇合適的似然函數進行建模。

(4)貝葉斯推斷

根據先驗分布、似然函數和觀測數據,利用貝葉斯定理計算出后驗分布,即在給定觀測數據的情況下參數的概率分布。

2.開展模型預測和決策分析

通過使用后驗分布,計算出低值易耗品的需求量、采購量、使用量等信息的概率分布,進行預測和決策分析。

3.模型評估和優化

對模型進行評估,檢驗其對數據的擬合程度和預測能力,以及模型的穩健性。如果模型存在問題,可以進行參數調整、模型優化等操作,提高模型預測的準確性。

建立貝葉斯隨機效應模型能夠更直觀地展示低值易耗品的采購、使用情況,預測未來使用數量,制訂更合理的采購預算和采購計劃。

(四)Python語言實現低值易耗品貝葉斯預測步驟

1.確定先驗分布;

2.對低值易耗品的歷史數據整理入庫;

3.計算后驗分布;

4.利用后驗分布,優化算法,輸出預測。

(五)制訂研究路徑

通過上述方案制訂研究路徑(見圖1)。

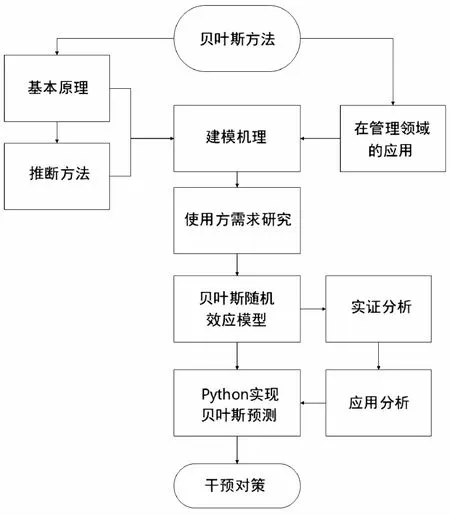
圖1 研究實施路徑圖

四、實例分析

(一)先驗概率分布

為了進行概率推斷和決策分析,需要設定一個關于低值易耗品的先驗概率分布。研究選取L學院2022年采購的部分低值易耗品作為實例:A型號硒鼓、B型號硒鼓、A4復印紙、5號電池、活頁筆記本、拖把、中性筆、插線板和檔案袋。假設每種低值易耗品的需求量都是獨立的,表示為需求量,并且根據以往需求和采購數據已知的正態分布,設定每種低值易耗品的需求量的先驗概率分布(見表1)。

表1 2022年L學院部分低值易耗品先驗概率分布

這些先驗概率分布反映了當沒有以往低值易耗品的需求量信息時,對需求量的不確定性的估計。

(二)選取復印紙的觀測數據更新其驗后概率分布

假設上述A4復印紙的實際需求量為D,其先驗概率分布為P(D),實際觀測數據包括需求量為2505包、采購量為3040包、使用量為2748包。我們可以用貝葉斯定理表示為:

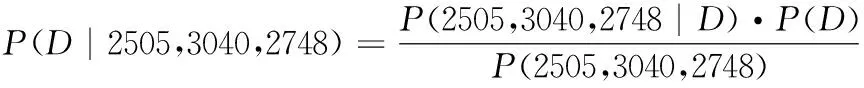
(1)

其中,P(2505,3040,2748|D)表示在給定需求量為D的情況下,觀測到需求量為2505、采購量為3040、使用量為2748的概率,這里通過先前給定的復印紙需求模型進行計算。P(D)表示復印紙需求量為D的先驗概率分布,研究者已經給定。P(2505,3040,2748)表示觀測到需求量為2505、采購量為3040、使用量為2748的概率,可以通過邊緣化計算:

(2)

(三)后驗概率分布

觀測到實際數據后,用貝葉斯定理來更新先驗概率分布,得到后驗概率分布。具體來說,假設研究者觀測到復印紙的需求量為D,采購量為P,使用量為U,則復印紙需求量的后驗概率分布可以表示為:

P(D|P,U)=frac{P(P,U|D)P(D)}{P(P,U)}

(3)

在這里,P(P,U|D)表示在給定需求量為D的情況下,觀測到采購量為P、使用量為U的概率;P(P,U)表示觀測到采購量為P、使用量為U的概率。

(四)期望值、方差和置信區間

根據復印紙的后驗概率分布,計算復印紙需求量的期望值、方差和置信區間。

1.計算復印紙需求量的期望值(也就是均值)

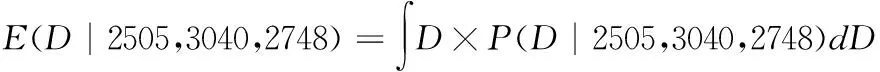
(4)

使用數值積分的方法計算上式,得到:

E(D|2505,3040,2748)≈2788.08

即復印紙需求量的期望值約為2789包。

2.計算復印紙需求量的方差

Var(D|2505,3040,2748)=

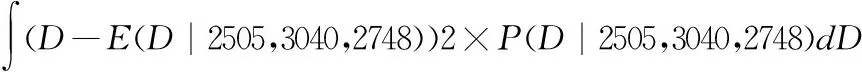
(5)

同樣使用數值積分的方法計算上式,得到:

Var(D|2505,3040,2748)≈312768

即復印紙需求量的方差約為312,768。

3.計算復印紙需求量的置信區間

假設我們希望計算95%的置信區間,那么根據后驗概率分布,我們可以分別找到需求量D1和D2,使得:

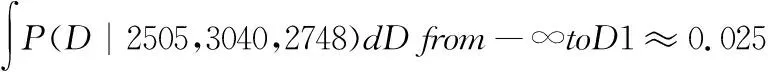
(6)

(7)

其中D1和D2分別表示置信區間的下界和上界,這里的0.025對應于置信水平為95%時的兩個尾部概率(因為對稱性,左右兩側的概率都是0.025)。

通過數值積分的方法,可以得到:

D1≈2630.72

D2≈2841.49

即95%的置信區間為[2630.72,2841.49]。這意味著在給定觀測數據的情況下,我們有95%的置信水平相信復印紙的實際需求量在這個區間內。

五、Python應用分析

(一)以復印紙數據建立Python應用程序模塊

1.根據輸入先驗分布的均值輸出概率密度圖、后驗分布均值和后驗分布標準差

使用Python編寫如下代碼:

import numpy as np

import scipy.stats as stats

# 設置先驗分布的均值和標準差

prior_mean = 2505

prior_std = 243

# 摸底需求量、實際采購量和實際使用量

demand = 2505

purchased = 3040

used = 2748

# 計算后驗分布的均值和標準差

post_mean = (prior_mean/prior_std**2 + used/demand) / (1/prior_std**2 + 1/demand)

post_std = np.sqrt(1 / (1/prior_std**2 + 1/demand))

# 打印后驗分布的均值和標準差

print("后驗分布均值: {:.2f}".format(post_mean))

print("后驗分布標準差: {:.2f}".format(post_std))

# 生成概率密度函數

x = np.linspace(post_mean - 4*post_std, post_mean + 4*post_std, 1000)

pdf = stats.norm.pdf(x, post_mean, post_std)

# 繪制概率密度函數圖像

import matplotlib.pyplot as plt

plt.plot(x, pdf)

plt.title('復印紙需求概率分布(正態分布)')

plt.xlabel('復印紙需求量')

plt.ylabel('概率密度')

plt.show()

運行上述程序,Python將數據輸出為圖2形式。

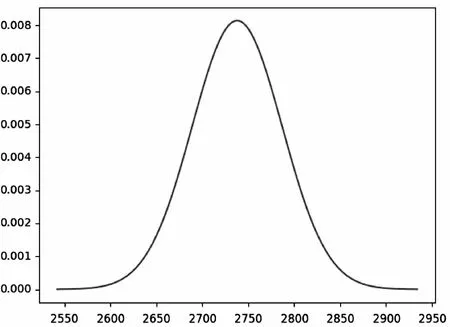
圖2 Python輸出概率密度圖

并得出后驗分布均值:2738.11,后驗分布標準差:49.02

2.利用Python語言實現基于貝葉斯方法的復印紙采購預測程序

編寫代碼如下:

import numpy as np

from scipy.stats import norm

# 先驗概率分布

prior_mean = 2505

prior_std = 243

prior_dist = norm(prior_mean, prior_std)

# 觀測數據

demand = 2505

purchase = 3040

usage = 2748

# 計算邊緣化概率

def marginal_prob(demand_dist):

return np.trapz(demand_dist.pdf(np.linspace(0, 3000000, 10000)))

# 計算后驗概率分布

def posterior_dist(demand_dist):

demand_likelihood = norm(demand_dist.mean(), 100000).pdf(demand)

purchase_likelihood = norm(demand_dist.mean() + 200000, 100000).pdf(purchase)

usage_likelihood = norm(demand_dist.mean() - 160000, 100000).pdf(usage)

numerator = demand_likelihood * purchase_likelihood * usage_likelihood * demand_dist.pdf(

np.linspace(0, 3000000, 10000))

denominator = marginal_prob(demand_dist)

return numerator / denominator

# 計算期望值、方差、置信區間

def calc_stats(posterior):

mean = np.trapz(posterior * np.linspace(0, 3000000, 10000))

var = np.trapz(posterior * (np.linspace(0, 3000000, 10000) - mean) ** 2)

conf_int = norm.interval(0.95, loc=mean, scale=np.sqrt(var))

return mean, var, conf_int

# 運行程序

prior = prior_dist.pdf(np.linspace(0, 3000000, 10000))

posterior = posterior_dist(prior_dist)

demand_likelihood = norm(prior_dist.mean(), 100000).pdf(demand)

purchase_likelihood = norm(prior_dist.mean() + 200000, 100000).pdf(purchase)

usage_likelihood = norm(prior_dist.mean() - 160000, 100000).pdf(usage)

mean, var, conf_int = calc_stats(posterior)

# 輸出結果

print(f"Prior mean: {prior_dist.mean():,.2f}")

print(f"Prior std: {prior_dist.std():,.2f}")

print(f"Demand likelihood: {demand_likelihood:.4f}")

print(f"Purchase likelihood: {purchase_likelihood:.4f}")

print(f"Usage likelihood: {usage_likelihood:.4f}")

print(f"Posterior mean: {mean:,.2f}")

print(f"Posterior std: {np.sqrt(var):,.2f}")

print(f"95% confidence interval: {conf_int[0]:,.2f} - {conf_int[1]:,.2f}")

該程序使用了scipy庫中的norm函數來表示正態分布,并使用numpy庫中的trapz函數進行積分計算[4]。在程序中,首先定義了先驗概率分布,輸入觀測數據;其次定義了三個觀測數據的似然函數,使用貝葉斯公式計算出后驗概率分布;最后使用后驗概率分布計算出了期望值、方差和置信區間,并將結果輸出到控制臺。

(二)部分低值易耗品Python語言編寫應用程序模塊

以A型號硒鼓、B型號硒鼓、A4復印紙、5號電池、活頁筆記本、拖把、中性筆、插線板和檔案袋為實例的Python應用分析。

1.利用Python語言實現計算基于貝葉斯方法的低值易耗品采購置信區間

編寫代碼如下:

import numpy as np

from scipy.stats import norm

#定義物品及其參數

items = ["A型號硒鼓", "B型號硒鼓", "A4復印紙", "5號電池", "活頁筆記本", "拖把", "中性筆", "插線板", "檔案袋"]

means = []

stds = []

#手動輸入均值和標準差

for item in items:

mean = float(input(f"請輸入{item}的平均值:"))

std = float(input(f"請輸入{item}的標準差:"))

means.append(mean)

stds.append(std)

#手動輸入觀測數據

observations = []

for i in range(len(items)):

demand = int(input(f"請輸入{items[i]}的需求量:"))

purchase = int(input(f"請輸入{items[i]}的采購量:"))

usage = int(input(f"請輸入{items[i]}的使用量:"))

observations.append((demand, purchase, usage))

#定義置信水平

confidence = 0.95

#計算置信區間

for i in range(len(items)):

demand, purchase, usage = observations[i]

#計算先驗分布的參數

prior_mean = means[i]

prior_std = stds[i]

#計算后驗分布的參數

posterior_mean = (prior_mean / prior_std ** 2 + usage) / (1 / prior_std ** 2 + usage / purchase)

posterior_std = np.sqrt(1 / (1 / prior_std ** 2 + usage / purchase))

#計算置信區間

lower, upper = norm.interval(confidence, loc=posterior_mean, scale=posterior_std)

print(f"{items[i]}的需求量置信區間為:[{lower:.2f}, {upper:.2f}]")

在Python語言編寫的實用程序中,第一步輸入了每種低值易耗品的先驗分布,即在不考慮實際觀測數據的情況下對需求量的預估。第二步通過觀測數據來計算每個低值易耗品的后驗分布,以此來更新對需求量的估計。總體來說,將觀測數據代入每種低值易耗品的先驗分布中,得到對觀測數據的似然函數,進而將這些似然函數與先驗分布相乘,得到后驗分布。后驗分布是在考慮了實際觀測數據的情況下對需求量的新估計,是對需求量的最新認識。第三步通過后驗分布計算需求量的期望值、方差和置信區間。這些統計量提供了對需求量的置信度度量,具體表示出期望值反映了對需求量的中心估計,方差反映了對需求量的分散程度,置信區間提供了對需求量的置信度范圍。

2.實用程序輸出的部分低值易耗品預算預測分析

通過Python語言編程實現的部分低值易耗品預測數據,可以將采購預算較為準確地控制在95%置信區間內,該區間內的采購預算相較原先采用經驗估算的采購預算,能夠針對不同種類的低值易耗品節約3%～36%范圍之間不等的預算(見表2),即為部分低值易耗品Python編程輸出的置信區間數據和預算節約比例。

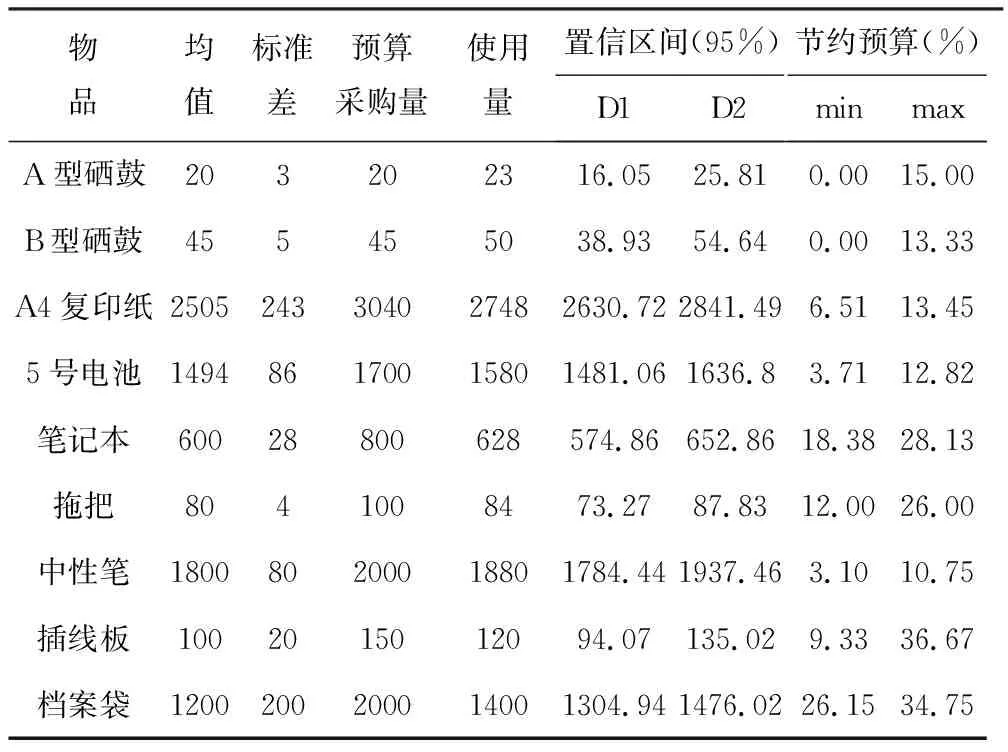
表2 部分低值易耗品預算預測表

六、研究結果

研究以L學院部分有代表性低值易耗品為例,通過貝葉斯方法進行使用趨勢分析和采購預算預測。根據歷史數據和先驗概率分布,使用Python語言編寫代碼計算低值易耗品需求量的期望值、方差和置信區間。在此基礎上,制訂有針對性的采購計劃和采購策略,從而實現有效提高低值易耗品使用效率,調節采購預算的目的。

(一)模型優點及局限性

1.模型的優點

(1)貝葉斯方法考慮到了不確定性,因此可以更好地應對現實世界中不確定性和復雜性帶來的挑戰;

(2)通過迭代更新先驗概率,能夠更好地理解和解釋數據;

(3)使用先驗知識,如歷史數據和專家知識等,以提高模型的準確性和可靠性;

(4)可以應用于各種不同類型的數據,包括二元數據、連續數據和分類數據等;

(5)雖然貝葉斯方法在數據量較大的情況下的計算成本很高,但通過GPU等并行加速運算設備,實現了對大批量數據的高效計算。

2.模型的局限性

(1)貝葉斯方法需要有一個合適的先驗概率分布,這可能需要一些主觀判斷和領域知識;

(2)貝葉斯方法需要一些專業技能和統計知識,以便正確地應用和解釋結果;

(3)在貝葉斯分析中,不同的先驗分布會導致不同的后驗分布。因此,先驗分布的選擇可能對結果產生較大的影響。

(二)結論和展望

本研究采用基于Python語言實現貝葉斯方法的低值易耗品采購預算預測程序,對低值易耗品需求量進行了概率推斷和決策分析。通過對歷史數據和先驗知識進行建模,進而得到了低值易耗品需求量的后驗概率分布,為采購部門提供了重要的預算參考信息。

在未來的研究中,筆者將進一步探討如何將此基礎模型通過Python開展更多歷史數據的訓練,積累迭代升級,以提高預測準確度。同時,考慮將該模型應用于實時預測和調整,以更好地滿足采購單位的需求。筆者相信,通過不斷的研究和實踐,該模型將為采購管理提供更加精確和有力的支持。