預應力陶瓷組合結構的抗侵徹性能研究

馬 昊,陳美多,苗春賀,王鵬飛,徐松林,2

(1.中國科學技術大學 中國科學院材料力學行為和設計重點實驗室,合肥 230027;2.中國地震局地震預測研究所 高壓物理與地震科技聯合實驗室,北京 100036)

陶瓷復合防護結構一般是以陶瓷為面板、以復合材料為背板膠粘而成的多層復合結構。對于復合裝甲,陶瓷強度的提升對增強結構抗沖擊性能具有決定性作用。陶瓷是一種高硬度、高抗壓性、低密度的脆性材料,能夠在各種極端溫度下工作,在工程結構的應用中備受關注[1-2]。近年來越來越多地應用于裝甲防護領域。但是,陶瓷性能的提升帶來脆性的增加不利于運動中的防護結構[3];同時金屬材料的性能目前已經應用得非常充分,很難帶來顯著的提升。為了實現現代輕量化和高韌性的要求,需要優化復合結構來提高抗侵徹過程中的能量耗散效率。由于目前陶瓷材料和復合材料的抗沖擊性能已經接近極限,因此采用新觀念設計出新的防護結構來提高抗侵徹能力就顯得尤為重要。

國內外學者在陶瓷材料抗侵徹性能的提升方面已開展大量的研究工作,取得了顯著的效果。鄒慧輝等[4]研究了陶瓷-活性粉末混凝土的抗侵徹性能,為陶瓷材料在重要防護工程的推廣使用提供參考。毛亮等[5]研究了鎢合金球形破片侵徹陶瓷/DFRP(dyneema fiber reinforced plywood)復合靶的彈道極限速度。殷文駿等[6]針對平頭彈高速撞擊陶瓷復合靶板問題,改進了理論模型。對于雙層的陶瓷復合裝甲,Zhang等[7]提出了一種雙層結構的解析設計方法,研究了雙層陶瓷裝甲防護效率的優化。Krishnan等[8]研究了具有完美材料模型的陶瓷復合裝甲有限元模型。Feli等[9]提出了一種新的陶瓷復合裝甲的彈孔數值模擬方法。在雙層復合裝甲的基礎上,Guo等[10]研究了Kevlar-29復合材料覆蓋層對雙層裝甲的影響,Xin等[11]研究了玻璃覆蓋層對透明陶瓷裝甲彈道性能的影響。Hu等[12]研究了一種抗平頭彈沖擊的多層復合裝甲,Wang等[13]對多層復合材料裝甲的設計與特性進行了研究。在復合結構抗沖擊性能的設計和分析方面取得了較系統的成果。為進一步提高復合結構的抗沖擊性能,近年來,研究人員提出采用預應力結構來提高材料強度,以更好地提高結構抗沖擊性能。Holmquist等[14]研究了預應力陶瓷模型以及設計薄厚兩種陶瓷靶板配置來了解預應力對于彈道沖擊性能的影響。吳雪等[15]基于LS-DYNA軟件模擬了預應力對于陶瓷材料抗侵徹性能的影響。Serjouei等[16-17]在試驗和仿真兩方面研究了預應力強度對雙層陶瓷復合裝甲的彈道沖擊性能的影響。研究結果表明：在預應力的作用下,陶瓷結構的抗侵徹性能得到了很好的改善。但是,這些研究中的預應力是由于結構擠壓而被動激發出來的,預應力值并不確定。

基于此,本文應用彈簧在復合結構內部對陶瓷施加已知的預應力,由彈簧、陶瓷,以及金屬邊框組合形成防護基元,將防護基元組合成預應力陶瓷組合結構。然后基于量綱分析方法確定該結構在高速沖擊下的殘余速度表達式,應用有限元數值分析方法分析了該預應力陶瓷組合結構的抗侵徹性能。

1 數值仿真模型

1.1 數值模型

新型預應力陶瓷組合結構主要是由組元板面和背板組成。其中,組元板面由多個正六邊形結構組元構成。圖1所示為單個組元的構成示意圖,從外到內依次為：金屬邊框、彈簧和陶瓷片;背板是一個實心的金屬板面,兩者在一起構成了本文所要研究的預應力組合結構。

(a) 金屬邊框

利用ABAQUS有限元仿真軟件建立防護結構計算模型。為簡化問題,侵徹過程的子彈采用平頭彈,直徑為12.7 mm,彈長為20 mm。組元板面由19個組元結構構成,每個組元中陶瓷片邊長為2 mm,彈簧長度為3 mm,金屬邊框的上下寬度為2 mm;組元板面和金屬背板的厚度均為3 mm。模型裝配圖如圖2所示。

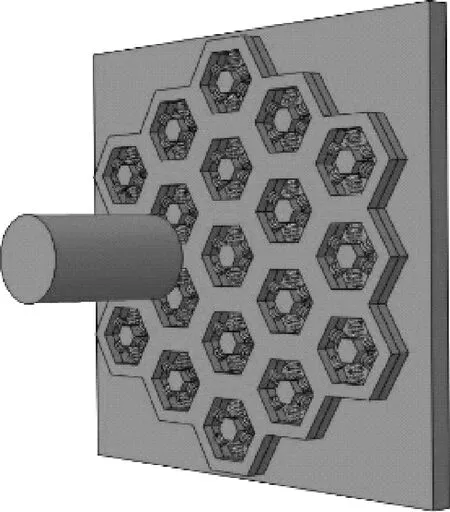
(a) 3維視圖

1.2 材料參數

子彈材料為Q235鋼,其參數為：密度7 850 kg/m3,彈性模量E=210 GPa,泊松比ν=0.3。背板材料為4340鋼,其參數為：密度7 830 kg/m3,彈性模量E=200 GPa,泊松比ν=0.29。由于侵徹過程屬于高速沖擊過程,在整個過程中,材料會處于大變形、高應變率狀態,材料的溫度也會出現激增現象,而J-C(Johnson-Cook)本構模型能夠很好地表征材料在沖擊作用下的動態力學行為,特別是侵徹過程中材料的力學響應行為。因此,4340鋼采用J-C本構模型和對應的動態破壞準則,該模型主要考慮了材料的應變強化效應、應變率效應和溫度引起對的屈服效應。

J-C本構模型為

(1)

Johnson-Cook破壞準則為

(2)

式中：εf為等效破壞應變;D1～D5為材料常數值;σ*=σH/σeq為應力三軸度,σH為平均應力;其他參數與式(1)中含義相同。

4340鋼J-C模型的本構參數和損傷參數的具體數值如表1所示。

表1 4340鋼的J-C本構模型參數[18]

模型中的陶瓷材料為碳化硅(SiC)：密度為3 205 kg/m3,剪切模量為193 GPa,泊松比ν=0.14。硬脆陶瓷材料的仿真中JH-1和JH-2本構模型使用較多,本文采用的是JH-2模型。因為JH-2模型在JH-1模型的基礎上考慮了材料強度的損傷劣化效應和材料梯度的破壞方程,可以實現脆性材料從不斷累積塑性應變下的軟化效應,對于侵徹過程中發生的大應變和高溫、高壓力情況,該本構模型能夠更好的模擬陶瓷材料的力學響應行為。JH-2本構模型包括強度模型、損傷模型以及狀態方程3個部分[19]。

強度模型為

σ=σi-D(σi-σf)

(3)

(4)

(5)

損傷模型為

(6)

(7)

壓力模型

(8)

(9)

式中：K1為初始體積模量;K2,K3為體應變系數;μ為體應變,μ=ρ/ρ0-1,ρ和ρ0分別為材料當前密度和參考密度;β為能量轉化系數;ΔU為彈性能的減少量。

SiC陶瓷的JH-2本構模型的參數詳如表2所示。

表2 SiC陶瓷JH-2本構模型參數[20]

1.3 預應力的施加

對于本文提出的新型組合防護結構,施加預應力的方式與傳統的通過直接對目標施加位移進行壓縮來產生預應力的方式有所不同。考慮到防護結構的特殊性,完成預應力的施加,首先要通過對單個彈簧施加位移約束,得到處于壓縮狀態的彈簧的應力數據。這里需要對結構中不同方位的彈簧都進行相同位移量的壓縮,在ABAQUS軟件中可以通過使用靜力學分析步進行計算。得到相應的應力數據后,根據結構中的單元完成應力數據文件的寫入,最后通過更改輸入文件的關鍵字完成預應力的施加。

1.4 有限元計算結果的驗證

陶瓷結構抗侵徹性能的數值分析很多,已有較為成熟的計算方法。本文進行的預應力陶瓷組合結構的數值仿真與已有的計算方法有不同之處,主要體現在預應力的施加過程中,本文主要是通過寫入應力文件的方式在初始狀態對結構賦予應力數值,不是通過直接位移壓縮需要施加預應力的部件進行添加。為了保證結果的有效性,有必要對數值計算方法進行驗證。為了驗證所提出的有限元模型以及數值模擬方法的準確性,將有限元模擬結果與文獻中已有的試驗數據進行比較。參考Zhang等研究中陶瓷和鋁合金組成的復合靶板的試驗數據,使用文獻中的材料參數進行數值模擬,得到的仿真數據與試驗數據的對比結果如圖3所示。

從圖3的數據可以看出,在無預應力條件下,隨著初始沖擊速度的增加,子彈的殘余速度也隨之增加,根據圖3仿真數據的曲線以及表3中的數據可知,仿真結果與試驗數據的殘余速度的差值不大,且誤差均在合理范圍之內。兩者之間的一致性證明了有限元模型以及方法的可靠性。

表3 仿真數據與試驗數據的對比

1.5 網格收斂性分析

為了保證結果的準確性,還需要對模型的網格進行收斂性分析。在該分析過程中,選取了5種不同的網格密度并統計其網格數量。對不同的網格數量模型進行相同初速度的子彈侵徹模擬,得到了參與速度結果如圖4所示。從圖4可知,當網格數量達到90 000后,繼續增加網格密度對結果的影響很小,當前網格的精度已經滿足計算要求。

圖4 網格收斂性分析

2 量綱分析

首先需要分析預應力對侵徹過程的影響機制。以Mises屈服準則為例。在主應力空間,Mises準則可表示為

(10)

式中,K1為試驗常數,也可以寫為

(11)

如圖5所示,預應力的施加使得材料的壓縮屈服極限從零預應力時的A點變化到預應力為σ時的B點,其強度得到了提升。但是,由于沖擊作用過程比較復雜,這種強度提升對材料侵徹性能的提高的相關性,需要進一步驗證。

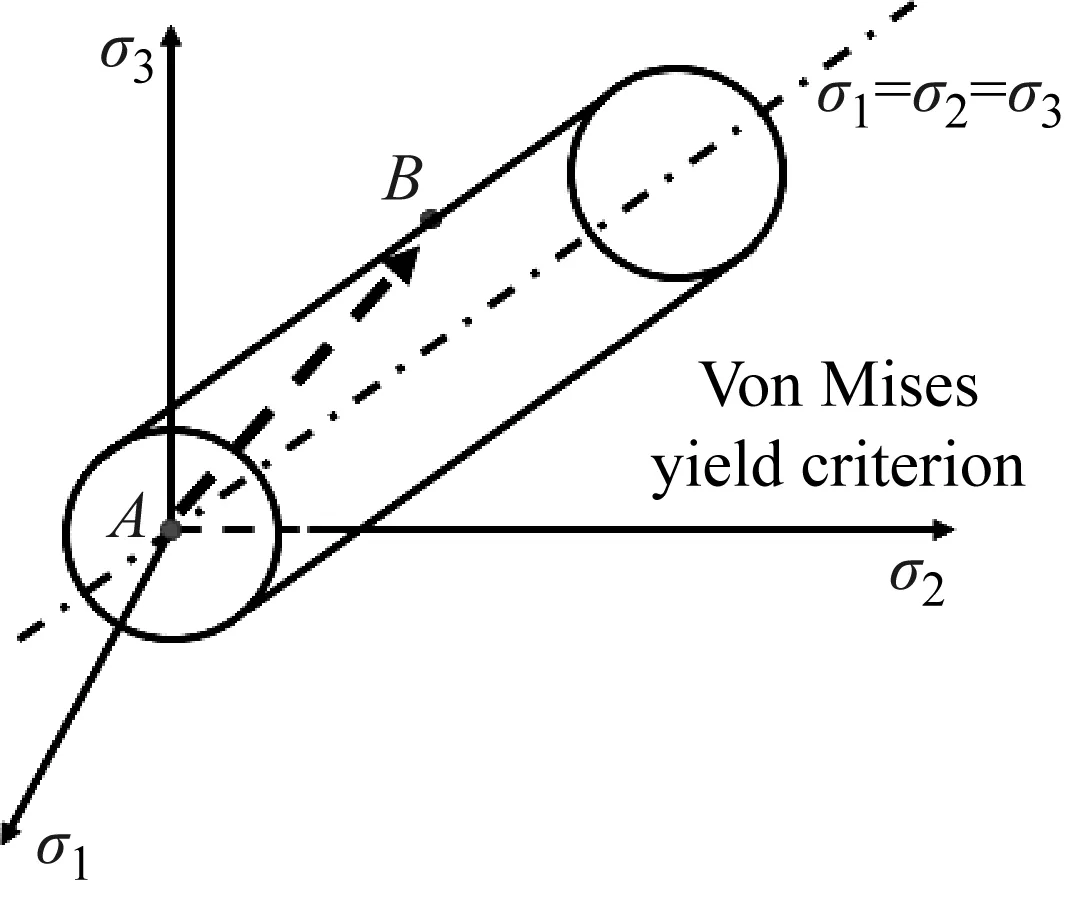
圖5 強度變化

其次,此復合結構的量綱分析中選擇殘余速度作為分析對象。基于圖1所示的幾何結構和圖2所示的數值分析模型,則殘余速度可表達為

Vr=f(ρp,Ep,νp;Vp,Vc;ρt,Et,Yt,νt;σ,ε)

(12)

式中：ρp,Ep,νp,Vp,Vc分別為子彈的密度、彈性模量、泊松比、初始速度和殘余速度;ρt,Et,Yt,νt分別為靶板的密度、彈性模量、屈服強度和泊松比;σ為彈簧施加的預應力;ε為靶板材料的斷裂應變。

以ρt,Vc和Yt作為基本量,則式(12)的無量綱形式為

(13)

由于侵徹過程主要與慣性作用(密度ρ)、靶板強度(屈服強度Yt)、材料的壓縮特性(Vp/Ct)以及結構中預應力的大小相關,因此侵徹過程的初步分析可集中于對這4個量的討論。引入靶板材料的波速Ct,則無量綱殘余速度的表達式為

(14)

將泊松比等其他材料參數代入,則可以得到殘余速度的初步表達式為

(15)

式中,m1,m2,m3,m4為材料參數,可結合試驗和數值分析綜合確定。

3 預應力陶瓷組合結構的抗侵徹性能

3.1 預應力的影響規律

該節進行了5種不同速度下的平頭彈侵徹過程的數值仿真計算,在每種速度下通過改變預應力大小來探究預應力對于組合結構的抗侵徹性能的影響規律。計算所得到的速度隨時間變化的結果曲線部分如圖6所示。圖7為與圖6相對應的速度下、不同預應力條件下,組元板在相同時刻的破壞程度對比圖。由此可見：

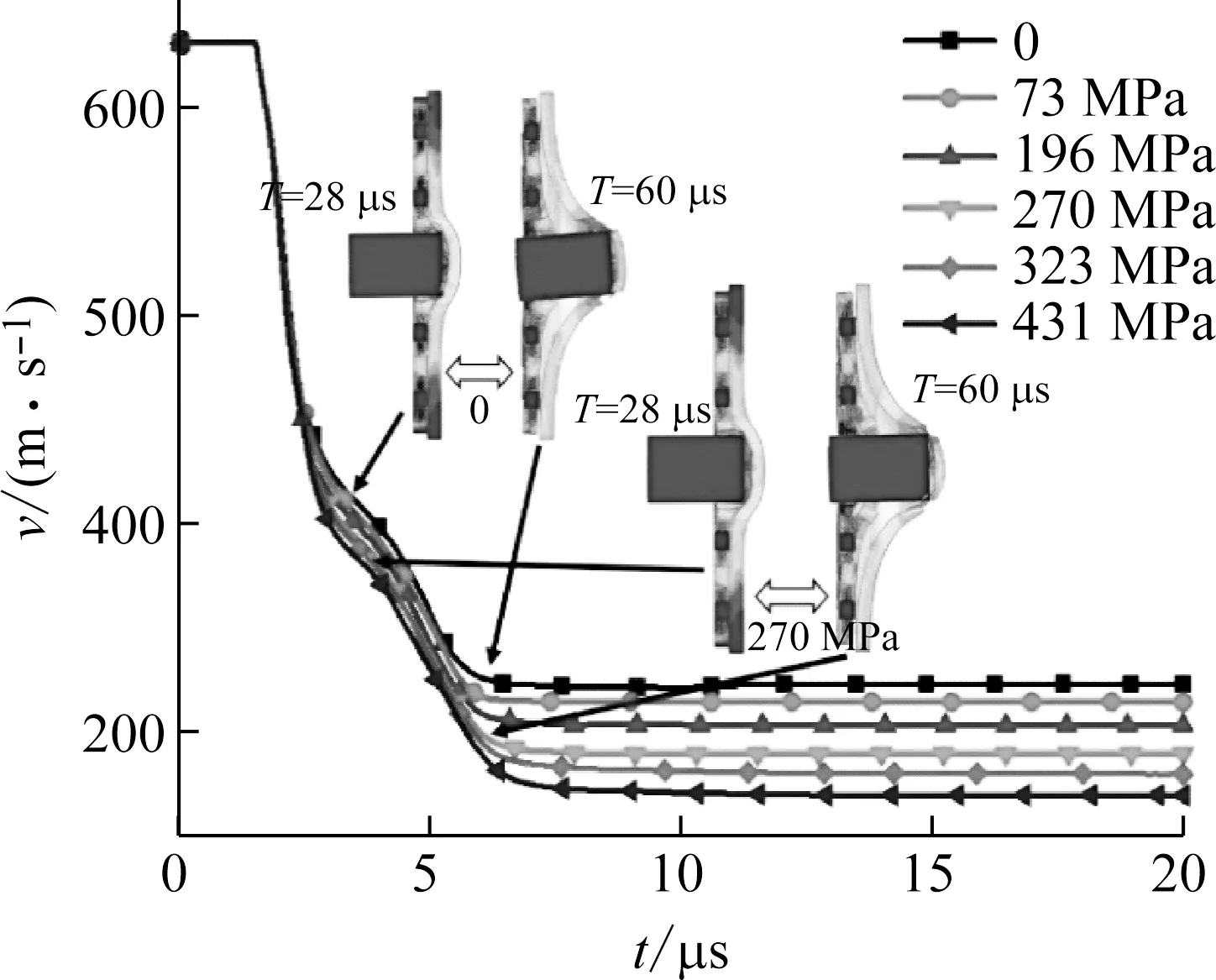
(a) 630 m/s

v=630 m/s,T=36 μs

(1) 圖6表明在平頭彈的侵徹過程中,子彈的速度從撞擊時刻開始隨著時間的增加逐漸減小,每條曲線都能夠很明顯的看到兩個拐點,即對應著防護結構的雙層板分別對子彈的抗侵徹過程;對比所得到的6條曲線,可以得知相對于無預應力條件,結構中彈簧施加的預應力能夠增強組合結構的抗侵徹能力;而且隨著結構中預應力的增大,子彈的侵徹殘余速度逐漸減小,即結構的抗侵徹能力隨著預應力的增加逐漸增強。

(2) 從圖7的破壞形貌圖可以直觀地得到與無預應力情況相比,含有預應力的組元板面的破壞程度更小,說明預應力作用下結構對子彈的抗侵徹能力有著明顯的增強;而且隨著結構中預應力的增大,在相同時刻,組元板上受到平頭彈沖擊部分的破壞程度在逐漸減小,即因超過損傷失效位移值而刪除的單元數量在逐漸減少,可以看出隨著預應力增大,結構的抗侵徹能力也在逐漸增強。

以上結果說明在該結構中預應力能夠很好的起到提高結構抗侵徹能力的作用。

3.2 面密度的影響

隨著對于多層靶板防護結構的深入研究,在保證防護性能的前提條件下,能夠盡量減小靶板的面密度也變得極其重要[21]。以第1章中的剛性彈侵徹組合板/金屬板的有限元模型為基礎,通過更改兩層板的厚度改變靶板的面密度,來探究該組合防護結構面密度對其抗侵徹性能的影響。這里需要說明的是組元板只改變了陶瓷和金屬邊框的厚度,彈簧的大小沒有改變,預應力大小為73 MPa。

兩層板的厚度范圍取為3～6 mm,分別進行組合可以得到16種不同的結果,對應16種不同的面密度,結果如表4所示。防護結構面密度的計算公式為

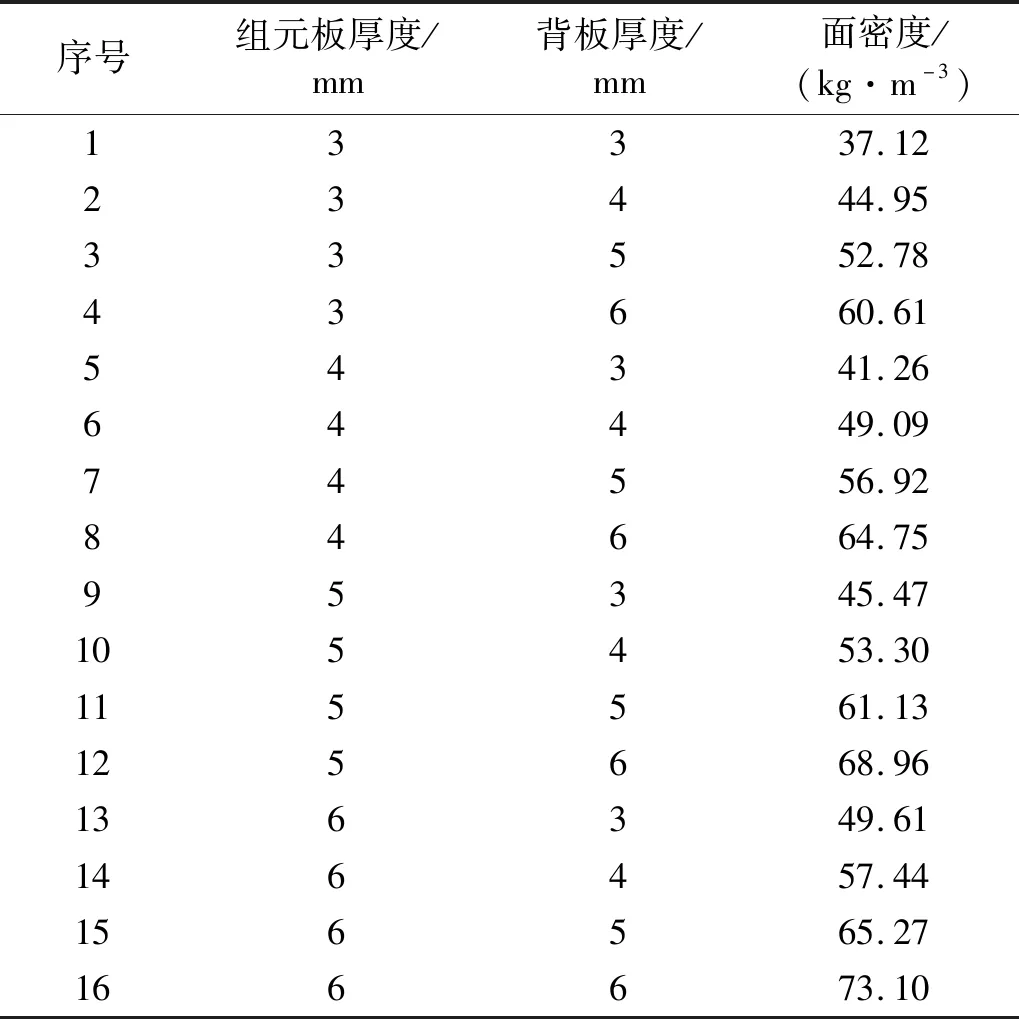
表4 不同靶板配置對應的面密度

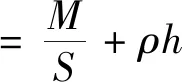
(16)

式中：M為組元板面的總質量;S為組元板面的總面積;ρ為背板的密度;h為背板的厚度。

以子彈的極限穿透速度V50為衡量指標來分析面密度的大小與防護結構抗侵徹能力大小的關系,從圖8可以得到：

(a) 更改組元板厚度

(1) 隨著面密度的增加,子彈的極限穿透速度也隨之增大,說明防護結構的抗侵徹能力也隨面密度的增大而增強。

(2) 增加背板厚度對應的子彈極限穿透速度的增幅比通過增加組元板厚度對應的極限穿透速度增幅大得多,結構的抗侵徹能力更強。

根據上述結果,考慮材料成本方面等問題,針對同一個問題時,可以通過增加組元板厚度與背板厚度比值,同時施加更大的預應力來達到目的。

3.3 彈體形狀的影響

考慮平頭彈和卵形彈這兩種不同形狀的彈體對組合結構的侵徹過程,主要是考慮防護結構對于不同彈體的抗侵徹能力。

對于子彈的設計是保證子彈的質量相同,相同速度下的動能相同。子彈的質量為M=19.8 g,讓子彈的直徑保持相同,主要通過改變子彈的長度來保證質量相等,子彈的幾何模型如圖9所示,靶板的配置采用的是3 mm+3 mm的組合,預應力的大小為73 MPa。

從圖10不同形狀子彈的速度隨時間的變化曲線中可以得到以下結論：在同樣的沖擊速度下,防護結構對平頭彈的抗侵徹能力很強,而對卵形彈的抗侵徹能力弱一些。隨著沖擊速度的增加,兩種子彈的殘余速度的差值逐漸減小。

(a) 600 m/s

4 討 論

基于無量綱分析方法確定侵徹影響因素的經驗公式。文獻[22-26]中關于侵徹影響因素公式大多是以彈坑深度為因變量的彈坑經驗公式,例如侵徹巖石和混凝等一些材料的侵徹深度經驗公式,本文考慮的變量是子彈完成侵徹過程后的殘余速度。考慮慣性、強度以及可壓縮性這3個影響因素。同時考慮到預應力的作用,加入了一項無量綱量——預應力與屈服強度相比。式如(15)所示,ε為金屬材料的動態斷裂應變,可取為0.2。

4.1 公式的驗證

為了驗證該公式,參考文獻[27]中關于單層金屬靶板與雙層金屬靶板的試驗數據來進行公式參數的擬合。考慮到試驗數據不包含預應力的影響以及子彈和靶板所使用的材料相同,所以擬合使用的公式忽略了式(15)中的慣性項和預應力項。圖11所示即利用公式和試驗數據計算得到的結果,可以看出該公式能夠很好的擬合試驗數據,參數的取值也處于合理范圍,說明該公式能夠較好地適用于不同情況下的平頭彈侵徹過程,具有一定的適用性。適用范圍：平頭彈,薄靶板,中低速侵徹。

4.2 無量綱參數的擬合

式(15)中臨界速度Vc需要進一步確定,其他參數根據材料性質已經能夠確定。基于文獻[28]提出的經驗公式,如式(17)所示。利用數值模擬得到的結果進行擬合計算,得到的曲線以及相關參數如圖12所示。

圖12 臨界速度的擬合結果

Vr=a(Vip-Vcp)1/p

(17)

式中：Vi為沖擊初速度;Vc為臨界速度;a和p的取值可以通過最小二乘法擬合初始速度和殘余速度求得。卵形彈撞擊靶板發生擴孔破壞：a=1;平頭彈撞擊發生沖塞破壞：a<1。

從圖11中的擬合結果可以清楚地得到靶板在無預應力條件下的臨界速度大小為538 m/s,將其代入式(15)中進行數值仿真計算結果的參數擬合。

殘余速度的表達式中的變量為沖擊初速度Vp和預應力σ,這里分別討論了沖擊初速度和預應力與參與速度無量綱量之間的關系。圖13所示即為利用殘余速度表達式進行擬合所得的結果圖。表5和表6中為擬合得到的參數結果,分別對應圖13(a)和圖13(b)。

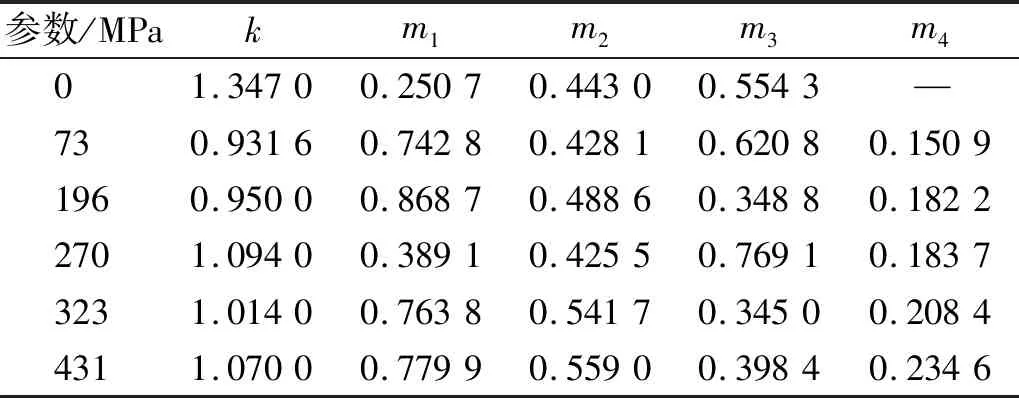
表5 Vr/Vc與Vp的擬合參數

表6 Vr/Vc與σ的擬合參數

(a) Vr/Vc與Vp的關系擬合結果

從圖13可以得知：利用殘余速度表達式(15)能夠較好的擬合由數值仿真計算得到的侵徹結果。圖13(a)表明：對于新型預應力組合結構,不同預應力大小下的曲線趨勢大致相同;計算所得殘余速度變化趨勢近似線性,應該是所選取的速度比臨界速度的取值大得多,Vr/Vc的快速上升階段沒有出現。圖13(b)表明：不同的初速度下曲線都逐漸趨于平緩,說明預應力對于結構的抗侵徹能力的提升隨著預應力的逐漸增大逐漸減小,預應力對結構抗侵徹能力的提升是有效的,但有限度。

通過表5、表6的擬合結果可知：擬合得到的指數參數m均在[-1,1],k的取值在也在合理范圍之內。表5表明,隨著預應力的增大,預應力無量綱參量項的指數逐漸增大,即預應力的影響增大。表6表明,隨著速度的增加,預應力無量綱參量項的指數逐漸減小,這與計算結果是相符的。

5 結 論

提出了一種新型預應力陶瓷組合結構,進行了較系統的有限元數值模擬。本研究適用于平頭彈中低速侵徹薄靶板過程。得到的主要結論如下：

(1) 在不同速度的侵徹過程中都表現出相對于無預應力情況,預應力條件下子彈的侵徹殘余速度更小,組元板的破壞程度更小,說明結構中添加的預應力能夠增強組合結構的抗侵徹能力;隨著結構中預應力的增大,子彈的侵徹殘余速度逐漸減小,組元板在相同時刻的破壞程度在逐漸減小,結構的抗侵徹能力隨著預應力的增加逐漸增強。因此,防護結構的抗侵徹能力隨著預應力的增加而增強。

(2) 隨著面密度的增加,子彈的極限穿透速度也隨之增大。相對于卵形彈,組合結構對平頭彈的抗侵徹能力較強;預應力對平頭彈的效果也要好一些。

(3) 提出了高速沖擊下的殘余速度表達式,并結合已有的試驗數據進行擬合計算,得到了較合理的參數取值。單層靶板和雙層靶板的試驗數據擬合較好說明該公式能夠適用于不同情況的侵徹過程,具有一定的適用性。分別討論了沖擊速度Vp和預應力σ與Vr/Vc的關系,擬合得到了較合理的參數。結果表明隨著預應力的增大,預應力無量綱參量項的指數逐漸增大,即預應力的影響增大;而隨著速度的增加,預應力無量綱參量項的指數逐漸減小。