時變工況下基于精細復合多尺度散度熵的旋轉機械故障診斷方法

盧太武,馬洪波,王先芝,陳改革

(1.西安郵電大學 通信與信息工程學院(人工智能學院),西安 710121;2.西安郵電大學 自動化學院,西安 710121)

在工程實際中,旋轉機械時常工作在時變工況下[1-2]。時變工況下的旋轉機械振動信號表現出明顯的時變調制的特點,難以準確地識別其運行狀態。近年來,許多學者對時變工況下機械設備動態信號處理及故障診斷方法展開了研究。例如,Feng等[3]提出了一種通過時變振幅和頻率解調譜來揭示滾動軸承時變故障特征頻率的方法。Xue等[4]將不敏感相對殘差特征與無量綱特征相結合,來檢測軸承的退化趨勢。Li等[5]提出了一種新的時變工況智能診斷框架和數據驅動故障特征分離方法,從所有信息中去除工況特征,并利用其余故障信息進行故障診斷。Zhao等[6]提出了一種無轉速階次跟蹤方法來獲取轉速信息,并采用包絡階次譜來尋找故障特征頻率。譚帥等[7]提出了一種基于周期記憶神經網絡的故障診斷方法,通過提取旋轉機械周期內故障特征,并利用記憶因子對周期內的傳遞規律進行選擇性遺忘,學習其周期內的時序特征,從而實現滾動軸承的故障診斷。

振動信號經過角域重采樣[8]轉為角域信號后,仍然受到噪聲等干擾源的干擾,影響故障診斷準確率。近年來,許多學者在這一方面做了大量的研究。Shao等[9]利用編碼器等角度采樣獲取發動機振動信號,采用角域同步平均法對原始振動信號進行去噪,利用角域信號包絡算法提取發動機早期故障特征。試驗結果表明,基于角域信號包絡算法的發動機故障檢測方法為發動機早期故障的檢測和診斷提供了一種新的方法。晏云海等[10]提出了基于循環譜分析的魯棒性滾動軸承故障特征提取方法,經熵加權降低無關干擾成分影響以有效提取故障特征。周小龍等[11]提出了基于變分模態分解(variational mode decomposition,VMD)和最大重疊離散小波包變換(maximal overlap discrete wavelet packet transform,MODWPT)相結合的信號去噪方法,首先利用VMD分解進行初次去噪,再利用MODWPT方法進行二次去噪,進一步提升信號的去噪效果。

故障診斷中特征提取直接影響故障診斷準確率,特征提取是故障診斷最重要的一步。目前,常用的特征有基于時域或頻域的統計特征、基于復雜度的特征、基于深度學習算法提取的特征等[12]。然而,為平穩信號設計的傳統時域和頻域特征提取技術總是難以提取到有效特征[13]。此時,表現信號復雜程度的非線性信號定量描述方法逐漸受到研究人員的青睞[14]。香農將熵定義為表征時間序列規律性、復雜性、周期性的指標。Richman等[15]提出樣本熵(sample entropy,SE),利用關聯維數的比率來衡量動力學復雜度。Chen等[16]對樣本熵進行改進,提出了模糊熵(fuzzy entropy,FE)。

結合Costa等[17]提出的多尺度理論,Li等[18]利用改進的Vold-Kalman濾波器對變轉速信號進行濾波,用多尺度樣本熵(multiscale sample entropy,MSE)提取故障特征。姜萬錄等[19]通過精細復合多尺度波動散布熵對液壓泵進行故障特征提取,通過粒子群優化支持向量機進行故障分類識別。Wang等[20]提出了一種新的熵值特征提取方法——多尺度散度熵(multiscale diversity entropy,MDE)。多尺度散度熵利用相空間中軌道的多樣性來量化時間序列的動力學復雜度。與其他多尺度熵值方法相比,MDE具有高一致性、強抗噪性、計算效率高的優點。雖然多尺度散度熵具有上述優點,但是在高尺度下,多尺度時間序列會大大縮短,導致散度熵沒有足夠的信息來估計動力學復雜度,在高尺度因子下表現出不穩定行為。針對多尺度散度熵的這一缺陷,本文通過引入精細復合多尺度過程提出了精細復合多尺度散度熵(refined composite multiscale diversity entropy,RCMDE),極大的提高了散度熵的特征提取能力。

本文將RCMDE應用到時變工況下旋轉機械故障診斷中,提出了一種時變工況下基于RCMDE的旋轉機械故障診斷方法。首先采用重采樣的方法將時域信號轉為角域信號,然后利用變分模態分解和獨立分量分析相結合的方法對角域信號進行去噪,最后采用RCMDE對去噪后的角域信號進行特征提取,將特征輸入LR(logistic regression)分類器中進行故障診斷。

1 理論基礎

1.1 散度熵

對于任意時間序列X={x1,x2,…,xi,…,xN},i∈[1,N],N為數據長度,散度熵(diversity entropy,DE)分為以下4個步驟計算。

步驟1相空間重構,基于Takens提出的相空間嵌入理論,設嵌入維度為m,則時間序列可以構建為一系列的空間軌線Y(m)。

(1)

步驟2計算相空間中相鄰軌線之間的余弦相似度d[yi(m),yj(m)],得到余弦相似度集合D(m)。

D(m)={d1,…,dN-m}=

{d[yN-m-1(m),yN-m(m)]}

(2)

(3)

步驟3設符號數為ε,將余弦相似度的值域[-1,1]劃分為ε個區間,表示為(I1,I2,…,Iε)。然后,統計余弦相似度落在每個小區間的概率(p1,p2,…,pε),顯然,小區間的概率之和為1。

步驟4根據步驟3得到的區間概率(p1,p2,…,pε),散度熵的計算方法如式(4)所示。

(4)

式中：ED(m,ε)為散度熵;Pk為余弦相似度的區間概率。

1.2 多尺度散度熵

為了揭示時間序列隱藏在不同尺度下的故障信息,散度熵與多尺度過程相結合,提出了多尺度散度熵。多尺度散度熵可通過兩個步驟計算。

(5)

式中,τ為尺度,且為正整數,通過調節其大小可得到不同尺度的時間序列。

(6)

式中：m為嵌入維度;ε為符號數。

1.3 精細復合多尺度散度熵

精細復合多尺度散度熵算法流程,如圖1所示。多尺度散度熵在高尺度下分解生成的時間序列的長度會大大縮短,使得散度熵沒有足夠的信息來估計時間序列的動力學復雜度,導致高尺度下的熵值不穩定。例如長度為2 048的時間序列在尺度為10時,分解后的子時間序列長度僅為204,長度縮減為原序列的1/10,難以為復雜度估計提供充足的信息。RCMDE通過滑動平均過程在高尺度下生成多個時間序列,利用多個時間序列進行估計,能夠更準確的統計相空間中的狀態概率,提高了多尺度散度熵在高尺度下的穩定性。例如長度為2 048的時間序列在尺度為10時,RCMDE分解出10個長度為204的子時間序列,狀態空間由200增大到1 999,極大的提高了狀態概率的準確性和穩定性。RCMDE(ERCMD)可按以下步驟計算：

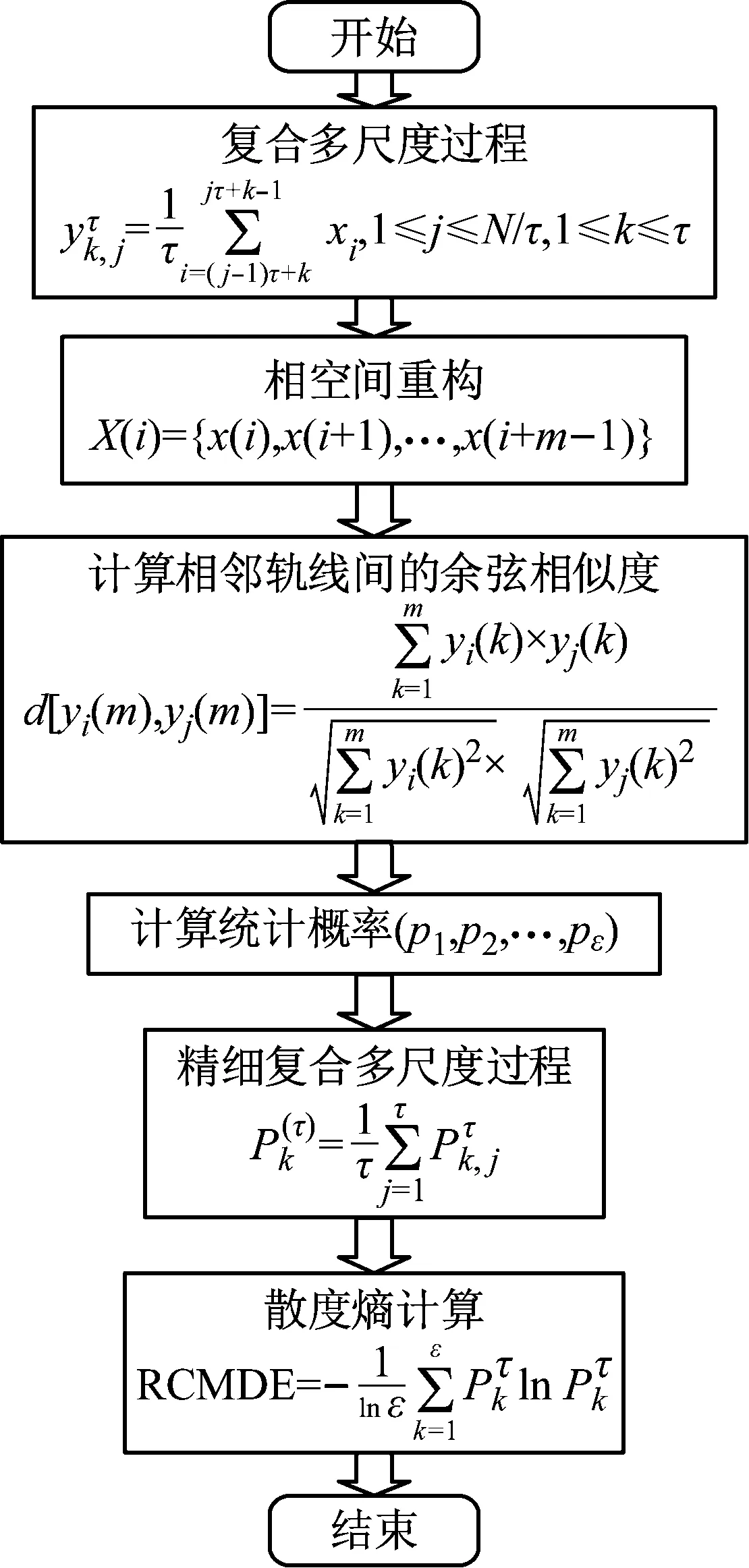
圖1 RCMDE算法流程圖

(7)

(8)

1.4 變分模態分解

VMD分解是一種可自適應確定序列模態分解個數的信號處理方法,目前已廣泛應用到振動信號降噪中。

假設序列由K個有限帶寬的模態分量μk(t)組成,VMD分解是尋找K個帶寬之和最小的模態函數μk(t),k∈{1,2,…,k}。步驟如下所示。

步驟1對模態函數μk(t)進行Hilbert變換得到解析信號,即

(9)

式中：t為時間,是大于0的正數;δ(t)為沖激函數;{μk(t)}={μ1(t),μ2(t),…,μk(t)}為分解得到的K個IMF(intrinsic mode function)分量。

步驟2各模態解析信號與算子e-jωkt相乘,即

(10)

式中,{ωk}={ω1,…,ωk}為各IMF分量μk(t)的中心頻率。

步驟3計算μk(t)的梯度的平方范數L2,并求出各IMF的帶寬。對應的表達式為

(11)

(12)

為了找到上述問題的最優解,引入二階懲罰因子α與Lagrange乘子λ(t),其中,懲罰因子α直接關系到信號能否準確重構。表達式為

L[{μk(t)},{ωk},λ(t)]=

(13)

(14)

式中,i∈{1,2,…,K}且i≠k。利用Fourier變換,完成時頻域的轉換,用ω-ωk代替ω,優化問題的解為

k∈{1,2,…,K}

(15)

中心頻率的更新方式如式(16)所示。

(16)

在變分模態分解后將得到一系列的IMF信號,通過峭度準則將IMF信號重構為觀測信號和噪聲信號。峭度準則的計算方法如文獻[21]所示。

1.5 獨立分量分析

利用峭度準則將IMF信號重構為觀測信號和噪聲信號后,采用獨立分量分析(independent component analysis,ICA)將觀測信號和噪聲信號進行解混生成去噪后的角域信號。ICA的計算方法如文獻[22]所示。

2 基于RCMDE的旋轉機械故障診斷框架

時變工況下的旋轉機械振動信號具有明顯的時變調制的特點,且易受噪聲等干擾源的影響。本文提出了一種時變工況下基于RCMDE的旋轉機械故障診斷方法。算法流程如圖2所示。首先采用重采樣的方法將時域信號轉為角域信號,然后利用變分模態分解和獨立分量分析相結合的方法對角域信號進行去噪,最后采用RCMDE對去噪后的角域信號進行特征提取,將特征輸入 LR 分類器中進行故障診斷。

步驟1通過對原始振動信號角域重采樣將時域信號轉為角域信號,消除轉速對原始振動信號的影響。

步驟2采用VMD和ICA聯合降噪的方法對角域信號進行降噪處理,消除噪聲等干擾源對角域信號的影響。首先對角域信號進行VMD分解生成多個IMF分量,其次根據峭度準則將IMF分量重構為觀測信號和噪聲信號,最后采用ICA算法進行解混,生成去噪后的角域信號。

步驟3采用RCMDE對去噪后的角域信號進行特征提取,將提取的特征輸入LR分類器進行故障診斷。

3 試 驗

3.1 試驗設置

本試驗采用位于西北工業大學的機械故障模擬器進行齒輪故障試驗。試驗臺及其示意圖如圖3(a)和圖3(b)所示。在該試驗中,使用電動機驅動一級斜齒輪減速器。該減速器由一對直齒錐齒輪組成,齒數比為18∶27。通過齒輪箱上方的加速度傳感器來獲取振動信號,采樣頻率設定為12 800 Hz。

(a) 試驗臺

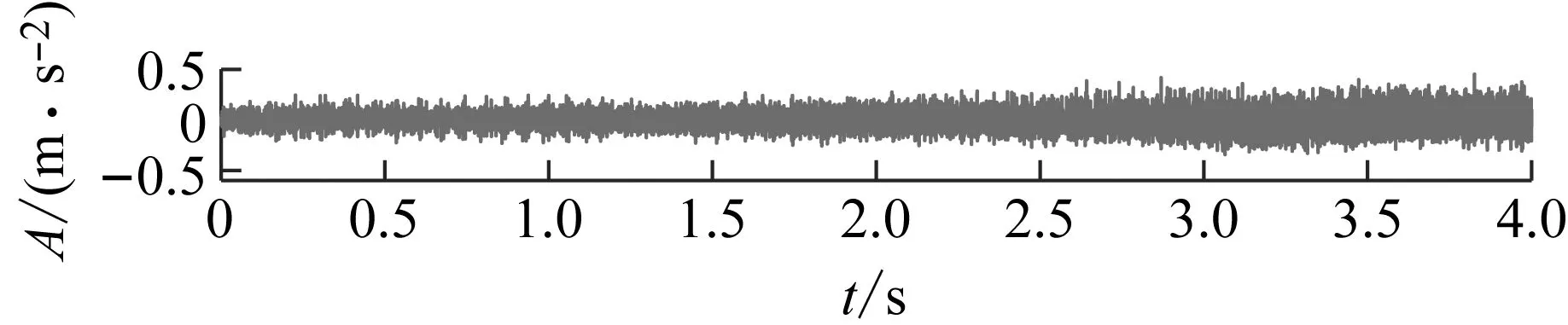
本試驗設計了4種類型的故障：主動齒點蝕(見圖4(a)),主動齒斷齒(見圖4(b)),主動齒缺齒(見圖4(c)),從動齒裂紋(見圖4(d))?？偣灿?種健康狀態的數據。每種健康狀態有200個樣本,總共有1 000個樣本,每個樣本長度為1 024個采樣點,時域振動信號和轉速如圖5和圖6所示。

(a)

(a) 主動齒點蝕

圖6 轉速圖

3.2 對比試驗

重采樣的角域信號如圖7所示,對角域信號采用VMD和ICA聯合降噪的方法進行降噪,去噪后的角域信號如圖8所示。

(a) 主動齒點蝕

(a) 主動齒點蝕

為了展示本文所提出的方法的優越性,用多尺度散度熵、多尺度排列熵(multiscale permutation entropy,MPE)、多尺度模糊熵(multiscale fuzzy entropy,MFE)、復合多尺度散度熵(composite multiscale diversity entropy,CMDE)、復合多尺度度排列熵(composite multiscale permutation entropy,CMPE)、復合多尺度模糊熵(composite multiscale fuzzy entropy,CMFE)、精細復合多尺度排列熵(refine composite multiscale permutation entropy,RCMPE)、精細復合多尺度散度熵、精細復合多尺度模糊熵(refine composite multiscale fuzzy entropy,RCMFE)等9種熵值方法分別提取去噪角域信號的故障特征,設置對比試驗。

熵值方法參數設置如表1所示。參數會影響熵值方法特征提取能力,進而影響故障診斷準確率。根據文獻[23],將每種熵值方法均設置為最優參數。RCMDE中共有嵌入維度、尺度因子和符號數3個參數,本文分別設置了3個試驗進行討論。3個試驗均采用固定兩個參數,調整另一個參數來觀察其對最終分類結果的影響,試驗結果如圖9所示。在圖9(a)嵌入維度試驗中,嵌入維度從1到8依次遞增,當嵌入維度大于4后,嵌入維度對準確率影響較小;當嵌入維度為6時,準確率最高,故將嵌入維度設置為6。在圖9(b)符號數試驗中,符號數從10到80依次遞增,符號數對準確率的影響較小;當符號數為20時,準確率最高,故將符號數設置為20。在圖9(c)尺度因子試驗中,尺度因子從10到80依次遞增,當尺度因子大于50后,尺度因子對準確率影響較小;當尺度因子等于60時,準確率最高,故將尺度因子設置為60。

表1 9種熵值方法參數設置

(a) 嵌入維度試驗

訓練樣本和測試樣本按1∶1劃分。為減小隨機性,每種方法將運行20次,其平均分類精度和標準差將作為評價每種方法性能的指標。

3.3 結果分析

如圖5所示,當齒輪在時變工況下運行時,振動信號頻率和幅值均表現出時變性,無法準確識別故障特征頻率,故障診斷準確率較低。重采樣后的角域信號如圖7所示,從圖7可以看出,重采樣的角域信號仍是非平穩信號,這是由于角域信號只是消除了轉速的影響,仍會受到噪聲等干擾源的影響。因此本文采用VMD和ICA聯合去噪的方法對角域信號進行去噪,去噪后的角域信號如圖8所示。從圖8可以看出,去噪后的角域信號趨于平穩,消除了噪聲等干擾源對角域信號的影響。

然后,采用RCMDE對去噪后的角域信號進行特征提取,并采用LR分類器來識別故障類型。同時為展示本文方法的優越性,還采用其他8種熵值方法進行特征提取,其結果如表2所示。

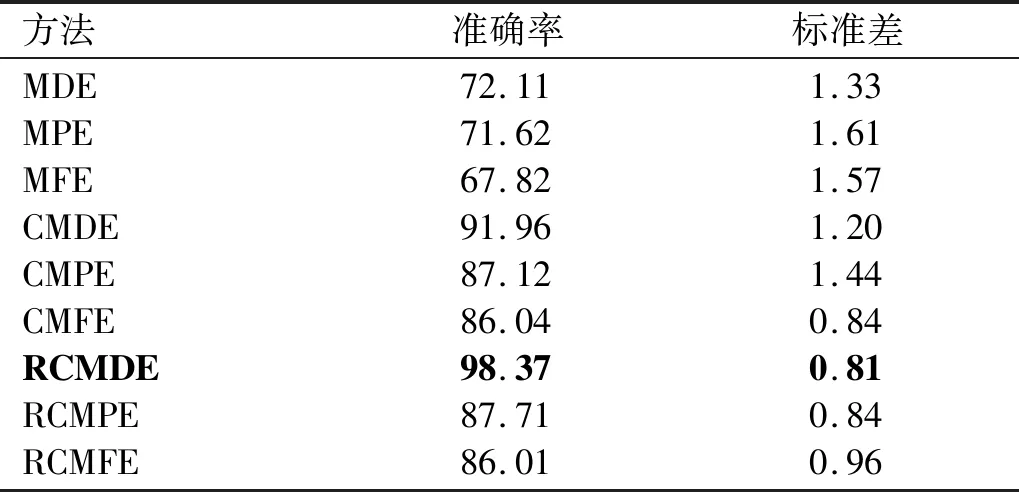
表2 去噪角域信號故障診斷準確率

從表2可以看出：

(1) 基于復合多尺度熵值方法進行特征提取的故障診斷準確率優于基于多尺度熵值方法進行特征提取的故障診斷準確率,例如CMDE方法準確率(91.96%)高于MDE方法準確率(72.11%)。這是由于滑動平均過程可以多次估計信號動力學復雜度以獲得穩定的熵值,分類器可以更容易地區分故障類型。

(2) 精細復合多尺度散度熵方法準確率(98.37%)高于復合多尺度散度熵方法準確率(91.96%),這是由于精細復合多尺度過程通過滑動平均窗口對狀態概率進行精確估計,進一步提高了熵值的穩定性,從而提高了故障診斷的準確率。

(3) 本文所采用的方法在所有9種方法中取得了最低的準確率標準差(0.81%),這說明本文所提精細復合多尺度散度熵具有最高的穩定性,能夠為LR分類器提供穩定的熵值特征,使得診斷結果的波動性最小。

綜上所述,本文所采用的方法在所有9種方法中取得了最高的分類準確率(98.37%)和最低的準確率標準差(0.81%),進一步證明了本文所提的基于RCMDE進行故障診斷的方法的優越性。

4 結 論

本文提出了時變工況下基于精細復合多尺度散度熵的旋轉機械故障診斷方法,首先,采用重采樣的方法將時域信號轉為角域信號,并利用變分模態分解和獨立分量分析相結合的方法對角域信號進行去噪。其次,采用RCMDE對去噪后的角域信號進行特征提取,然后將故障特征輸入LR分類器中識別故障類型。通過與其他8種熵值方法進行對比試驗,結果表明本文所提出的方法具有最高的準確率和最小的標準差,證明了本文所提方法的優越性。