高墩大跨連續梁橋內力位移雙控減隔震體系的有效性初探

唐文樂,張俊平,謝柱堅,蘇建旭,王 波

(廣州大學 工程抗震研究中心,廣州 510006)

減隔震技術應用于橋梁工程已經超過30多年,減隔震設計逐漸成為一種有效的地震響應控制方法[1]。連續梁是一種常見的、經濟的橋型,但如何將減隔震技術運用于高烈度區高墩大跨連續梁橋的設計中,目前仍存在一些問題,主要表現為墩底內力與梁端位移有效控制的矛盾。大跨度連續梁的隔震設計通常采用鉛芯橡膠支座或摩擦擺支座,在有效削減墩底內力的同時,會增大梁端的位移[2-3]。另一方面,隨著跨徑的增大,梁體自身的慣性力迅速增大,地震作用下梁端位移會進一步放大,這對于柔性高墩大跨連續梁橋尤為突出[4-5]。過大的梁體位移不利于伸縮縫的設計,會導致梁體碰撞、落梁等問題發生。

在國內外,有一些使用黏滯阻尼器和隔震支座組合來控制高墩大跨連續梁的墩底彎矩和梁端位移的工程實踐。如在智利修建的Amolanas大橋橋墩高達99.6 m,采用摩擦滑動支座和兩側橋臺處設置黏滯阻尼器的組合方案,取得了較好的減震效果[6];美國加利福尼亞州南部91/5公路立交橋經過綜合比較分析,表明組合使用橡膠支座和黏滯阻尼器是該橋的最優減震方案[7];Li等[8]以一等截面變高墩大跨連續梁為工程背景,搭配使用鉛芯橡膠支座和黏滯阻尼器能使縱橋向各橋墩的滯回能力消耗趨于平均,較好地控制高墩地震反應;魯傳安等[9]采用雙曲面球型隔震支座和黏滯阻尼器對墩高為51 m和31 m的3跨連續梁進行減隔震設計,使各墩位移趨于一致,與原結構相比縱向位移最高減小了70%。以上案例均說明在高墩大跨連續梁橋的抗震設計中,組合使用隔震支座和黏滯阻尼器可一定程度的實現墩底內力-梁端位移雙控的效果。但是,黏滯阻尼器加工要求較高、可靠性較差等缺陷一直未得到完全解決,漏油等密封問題仍然困擾著工程界。如在2022年9月5日四川瀘定6.8級地震震后調查中發現,瀘定縣燕子溝鎮某建筑所使用的黏滯阻尼器出現剪切破壞,連接節點完全拔出[10]。

撐架是連續梁橋頂推施工和懸臂澆筑施工常用的裝置。當頂推施工時,將撐架安裝在橋墩頂部,可以有效削減梁體負彎矩、減小臨時墩的數量;懸臂澆筑施工時,通常利用撐架立模現澆0#塊,并作為掛籃施工的臨時工作臺。但其作為臨時結構,在梁體合龍后多拆除。為物盡其用,一些工程采取永臨結合的方式,將其作為永久結構的一部分,以減少施工工序、削減支點的負彎矩峰值,如我國1976年采用頂推法施工的東莞市萬江大橋,就是一座撐架式混凝土連續梁橋[11]。撐架式連續梁可以有效地減小梁體跨徑和內力峰值,但撐架的防撞性能、美觀性較差,隨著技術的進步,逐漸淡出了工程界的視野。

基于上述分析,本文基于撐架式連續梁橋結構特點和耗能減震的思想,提出一種采用低屈服軟鋼材料制備撐架、并與摩擦擺隔震支座組合的減隔震體系。首先推導了撐架結構等效阻尼比的計算公式,然后通過Midas/Civil平臺,基于阻尼比公式對比研究了4種減隔震方案的地震響應,并對撐架結構進行了參數分析。最后,對附加撐架結構的連續梁進行靜力性能分析,探討了撐架和摩擦擺支座組合以實現高墩大跨連續梁橋墩底內力和梁端位移雙控的有效性,為高墩大跨連續梁橋的防震設計提供一種新方法和思路。

1 撐架的等效阻尼比

從施工角度確定撐架尺寸、構造,然后研究其動力行為。撐架的簡化計算圖式同圖1所示。圖1中：V為撐架承受的剪力;l為撐架等效為一個斜撐的撐架長度;a為位移角;θ為撐架等效為一個斜撐的支撐角度。撐架的設計原理與耗能減震裝置類似,本構模型可采用如圖2雙線性模型。基于能量等效的原則,在一個振動循環內令等效黏性阻尼比做的功等于實際阻尼做的功,可得到撐架的等效阻尼比ξe

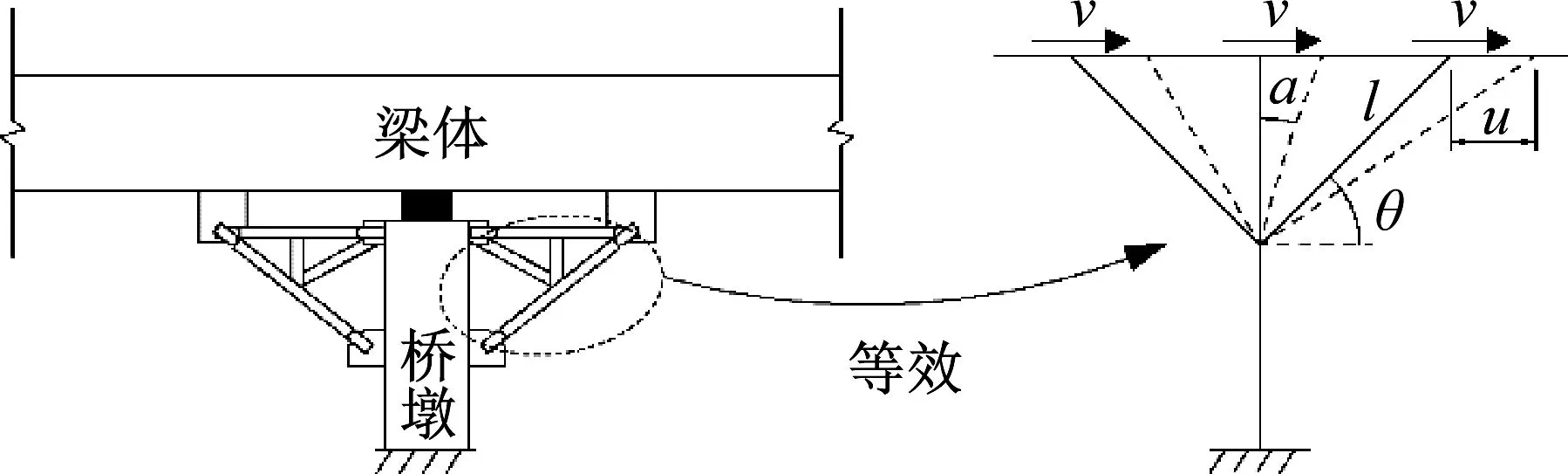
圖1 撐架計算簡圖

圖2 撐架等效阻尼比

(1)

式中：ED為實際阻尼在一個循環內做的功,表示為滯回圈的面積;Ec為結構對應于最大位移的應變能,表示為滯回曲線上的最大位移點與原點連線向位移軸投影得到的三角形面積。等效阻尼比可進一步寫為

(2)

式中：Qd為特征強度,即滯回曲線正向與剪力軸相交值;umax為最大位移;Fmax為umax對應的最大力;uy為屈服位移;Fy為uy對應的屈服力;K0為初始剛度;d為剛度因子,取值為0.02。對撐架進行簡化分析,則有

(3)

umax=alsinθ

(4)

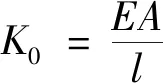
(5)

Fy=K0uy

(6)

式中：E為材料的彈性模量;σy為材料的屈服強度;A為撐架等效截面面積。將式(3)～式(5)和式(6)代入式(2),整理得

(7)

根據等效阻尼比公式式(7)可知,支撐角度θ影響不大,從施工角度分析,可設計為45°,方便其組成構件的設計。a類似于框架結構的層間位移角,參照相關規范可取最大值1/50[12]。在采用Q160LY軟鋼材料的情況下,依據相關工程經驗,確定撐架的等效阻尼比為8%～12%,由此可確定撐架長度和等效截面面積的合理區間,如圖3所示。

圖3 撐架等效阻尼比參數分析

2 減隔震方案比選

采用跨徑布置為(54+90+54)m的典型3跨連續梁,梁體為變高度單箱雙室箱形截面,箱梁頂寬17 m,箱梁底寬12 m,墩頂梁高5.2 m,跨中及邊墩墩頂梁高2.5 m,邊墩高20 m,中墩高40 m,采用有限元軟件Midas/Civil建立的全橋模型如圖4所示。作為初步研究,本文主要探討該體系的有效性,為此,利用現有的強震記錄,選取El-Centro波、Taft波和Northridge波3條地震動數據,使其覆蓋連續梁的前幾階頻率(1階頻率0.53 Hz,2階頻率1.08 Hz,3階頻率1.13 Hz),對結構進行地震響應時程分析,如圖5和圖6所示。

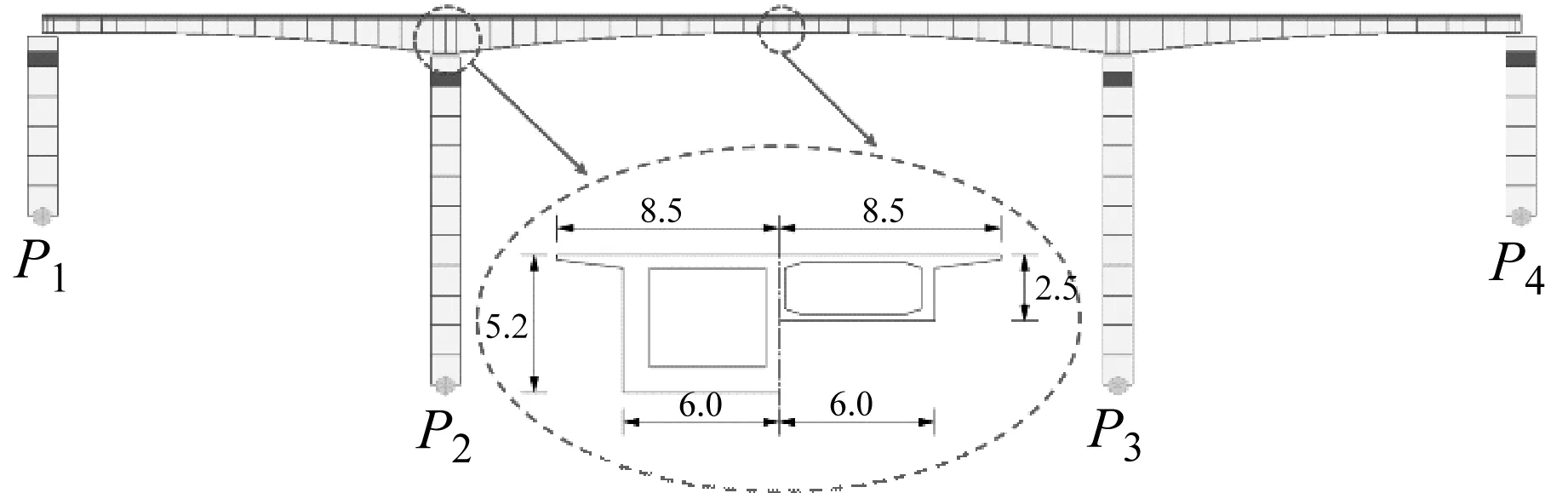
圖4 三維有限元模型(m)

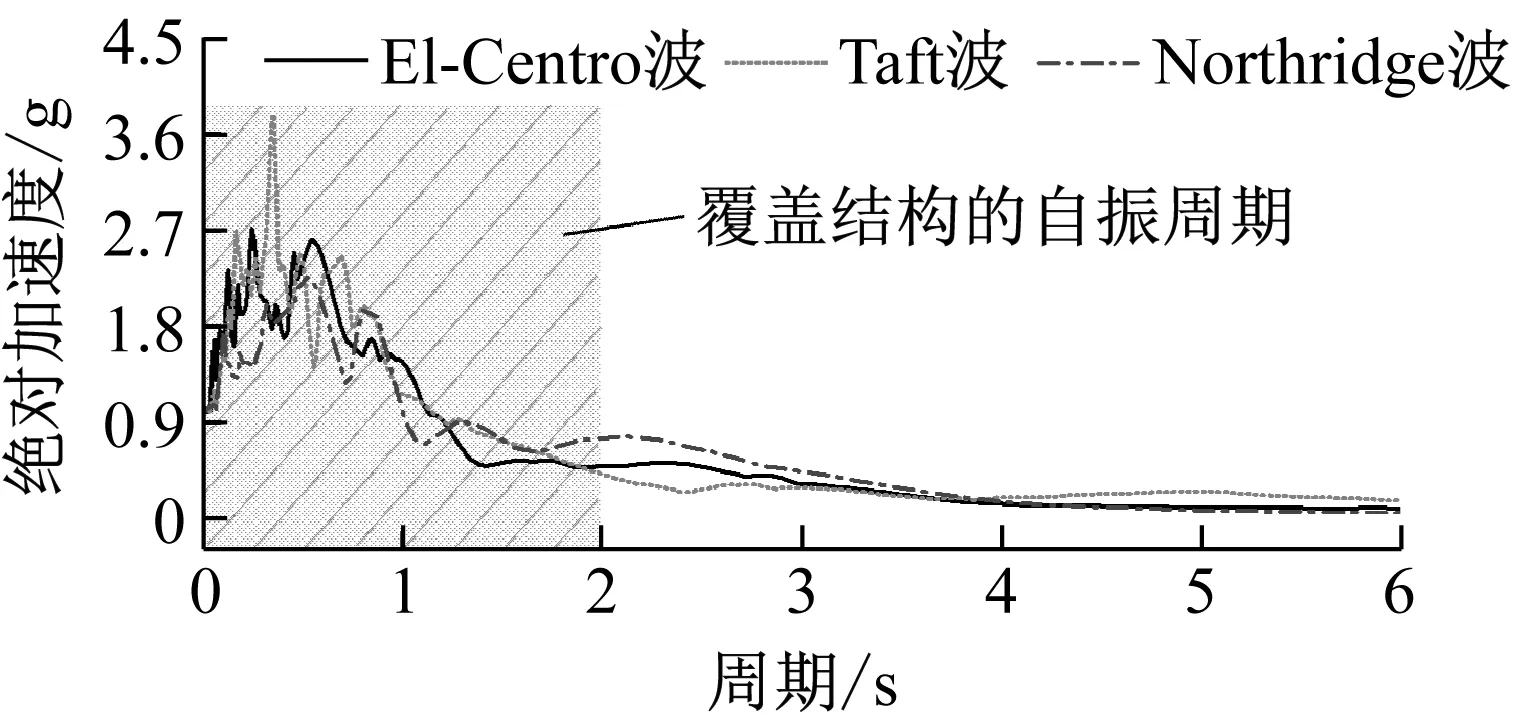
圖5 加速度反應譜

圖6 地震動時程圖

對于大跨連續梁橋,常用的隔震裝置有鉛芯橡膠支座和摩擦擺支座。為減小梁端位移,還可采用隔震和減震裝置組合的方式,如鉛芯橡膠支座+黏滯阻尼器。此外,鑒于摩擦擺支座實際工作時發生單擺運動,與提供軸向拉壓阻尼力的黏滯阻尼器不完全適配,本文提出了摩擦擺支座和撐架組合的減隔震體系。幾種減隔震方案的要點如下：

抗震方案,P1,P2,P3和P4墩均設置普通支承。

減隔震方案1,P1,P2,P3和P4墩均設置鉛芯橡膠支座。

減隔震方案2,P1,P2,P3和P4墩均設置摩擦擺支座。

減隔震方案3,在減隔震方案1的基礎上,在梁底和P1,P4之間增設縱向黏滯阻尼器。黏滯阻尼器的阻尼系數為3 000 kN·s/m,阻尼指數為0.2。

減隔震方案4,在減隔震方案2的基礎上,在梁底和P2,P3墩兩側設置撐架。以撐架等效阻尼比9%為目標值,撐架長度為6 m,等效截面面積為1 100 mm2,采用Q160LY軟鋼,彈性模量為2.06×105MPa,屈服強度為(160±20)MPa。

其他參數如表1、表2所示。

表1 鉛芯橡膠支座相關參數

表2 摩擦擺支座相關參數

3 動力響應及靜力行為比較

3.1 動力響應對比

本文主要研究的是高墩大跨連續梁的內力位移雙控體系,評價指標為墩底彎矩、墩底剪力和梁端位移。考慮到隔震裝置和減震裝置的非線性特征對結構地震響應的影響,采用非線性時程分析方法進行分析。假定該橋按地震基本烈度為Ⅷ度進行設防,分別沿縱橋向和橫橋向輸入地震動,地震動峰值加速度均調整為0.3g,得到抗震方案、減隔震方案1、減隔震方案2、減隔震方案3和減隔震方案4各橋墩關鍵截面動力響應,結構地震響應幅值取3條地震動的最大值,如表3所示。

表3 各方案地震響應結果

3.1.1 墩底彎矩

相較于抗震方案,減隔震方案1和減隔震方案2均能顯著減小各橋墩墩底彎矩,減震率分別為42%～72%和47%～80%,說明兩種支座選型合適。在減隔震方案3中,相較于抗震設計,組合使用鉛芯橡膠支座和黏滯阻尼器的橋墩墩底彎矩的減震率保持在50%～70%。減隔震方案3在減隔震方案1的基礎上增設了黏滯阻尼器,阻尼器的阻尼作用使地震力在全橋進行了重新分配,P1和P4縱橋向墩底彎矩相對于減隔震方案1增大了10%,P2和P3彎矩則減小了17%,各墩橫橋向墩底彎矩則無明顯變化。這是因為本文在選用黏滯阻尼器時,主要考慮控制梁端位移,僅在縱橋向單排布置,阻尼力增大了由上部結構傳遞給橋墩的慣性力,導致P1和P4墩墩底彎矩有所增大、P2和P3墩底彎矩有所降低。

在減隔震方案4中,可以看到設置撐架后,與抗震方案相比,減震率在30%～79%。與減隔震方案2相比,各墩墩底彎矩均有所增加,增加率為13%～38%,增幅不大。其中中墩P2和P3的彎矩較邊墩P1和P4的大,說明撐架在提供附加阻尼時還提供了一定附加剛度,提高了P2和P3墩的抗推能力,橋墩承受更大的內力,但P2和P3墩底彎矩與P1和P4墩底彎矩差距不超過19%。

3.1.2 墩底剪力

由表3可知,在抗震方案中,墩底最大剪力為40 889 kN,在減隔震方案1中,僅使用鉛芯橡膠支座的最大剪力為6 206 kN,減震率為85%;在減隔震方案2中,僅使用摩擦擺支座的最大剪力為7 289 kN,減震率為82%。在減隔震方案3和減隔震方案4的雙控體系中,橋墩墩底剪力峰值均有所增加,分別為6 828 kN和7 719 kN,仍遠小于抗震方案的最大剪力。說明在高墩梁橋中,無論是采用黏滯阻尼器還是設置撐架進行減震,橋墩受到的剪力會有所增加,但這種增加在與隔震支座組合使用的減隔震方案3和方案4中相對較小,可以通過隔震支座進行控制。

3.1.3 梁端位移

表3顯示了地震作用下,各方案在縱橋向的最大梁端位移,其中減隔震方案1和減隔震方案2的梁端位移均較大,分別達到了0.379 m和0.498 m,表明單純的隔震設計會明顯增加梁端位移,這是因為隔震設計使結構整體剛度變柔,通過釋放梁體和橋墩之間的約束,將上部結構和橋墩隔離開來,使結構的變形集中到隔震裝置處,從而減少墩底的內力。

在使用黏滯阻尼器后,減隔震方案3的最大梁端位移為0.208 m,相較于減隔震方案1減小了45%,但黏滯阻尼器的限位能力是以高的阻尼系數為代價的,阻尼系數太高會帶來加工困難等問題。在設置撐架后,減隔震方案4的最大梁端位移降至0.250 m,相較于減隔震方案2減少了50%,可見撐架與摩擦擺支座組合使用可以有效限制梁端位移。

由以上對比分析可見：對于大跨高墩連續梁體系,減隔震方案3和方案4的減隔震效果明顯優于減隔震方案1和方案2,鉛芯橡膠支座與黏滯阻尼器組合而成的減隔震體系、摩擦擺支座和撐架組合而成的減隔震體系均具有較好的墩底內力與梁端位移的雙控效果。但從震后復位能力來看,橡膠支座和黏滯阻尼器不具有復位能力,震后殘余變形較大,而摩擦擺具有較好的限位復位能力,構造簡單,性能可靠,且可以較方便地通過材料和幾何參數來控制撐架所提供的附加阻尼和剛度,是一種適用于高墩大跨連續梁防震的雙控體系。

3.2 撐架參數分析

撐架參數如截面積、長度等對減隔震體系的墩底內力、梁端位移雙控影響較為明顯,為此,選擇不同撐架長度和等效截面面積兩兩組合分別建立有限元模型,以減隔震方案4縱橋向墩底最大彎矩和梁端最大位移為控制目標進行參數分析。

由圖7可知：在相同的等效截面面積下,隨著撐架長度l從6 m增加到10 m,墩底的最大彎矩逐漸減小,減小率分別為14%,15%和16%;在相同撐架長度下,隨著等效截面面積A從1 000 mm2增加到1 600 mm2,墩底的最大彎矩則緩慢增加。其原因在于,對于設置撐架的橋墩,橋墩所分配到的地震力會增大,且附加剛度隨等效長度的增加而減小,隨等效截面面積的增加而增大。從圖8中可以得到,隨著等效截面面積和撐架長度增加,梁端位移均增大,限位效果變差。撐架的限位能力主要依賴軟鋼材料的屈服耗能,設計時主要根據梁端位移的設計需求,初步選擇軟鋼材料,再通過撐架等效阻尼比公式選擇合適的撐架長度和等效截面面積范圍,在保證其限位能力的同時,避免各墩彎矩分布差異太大。

圖7 不同撐架長度下墩底最大彎矩隨等效截面面積的變化

圖8 不同撐架長度下梁端最大位移隨等效截面面積的變化

3.3 靜力性能分析

摩擦擺支座與撐架組合而成的減隔震體系,除了可以有效降低地震響應外,靜力作用下梁體支點截面負彎矩峰值也可得到大幅度的削減,梁高和橋墩截面需求降低,動力響應還會進一步降低,起到良性循環作用。相較于減隔震方案2,減隔震方案4在P2,P3墩增設撐架后,在自質量和二期恒載作用下,支點截面負彎矩峰值從384 493 kN·m下降到280 681 kN·m,減小幅度高達27%(見圖9),相應的,活載彎矩也會相應降低。初步估算,梁高可由原來的5.2 m降至4.6 m,由此也使橋墩尺寸相應減小,橋墩地震動力響應進一步降低。

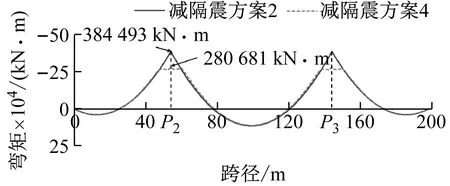
圖9 恒載作用彎矩分布圖

另一方面,從工程實施角度來看,鉛芯橡膠支座與黏滯阻尼器組合減隔震體系中,鉛芯橡膠支座尺寸較大,算例中鉛芯橡膠支座直徑為2 m,導致橋墩帽梁尺寸不得不隨之增大,約為15 m×3 m,而對應的摩擦擺支座尺寸僅為1.07 m×1.07 m,帽梁尺寸為14.0 m×2.2 m,這一點隨著墩高的增大,意義無疑是很大的。

4 結 論

本文提出了摩擦擺支座和撐架組合使用的減隔震體系,對于高墩大跨連續梁的墩底內力、梁端位移的雙控具有突出的效果,在靜力行為和施工方面也極具優勢,初步研究的主要結論如下：

(1) 推導了撐架結構等效阻尼比的簡化計算公式,基于此公式對撐架進行了參數分析,通過對鉛芯橡膠支座方案、摩擦擺支座方案、鉛芯橡膠支座+黏滯阻尼器減隔震方案以及摩擦擺支座+撐架減隔震方案進行了方案對比,驗證了該體系對高墩大跨連續梁橋內力位移雙控的有效性。

(2) 撐架的充分利用,永臨結合,減少施工工序,同時降低了靜力作用下支點截面負彎矩,梁高和橋墩的尺寸需求也會隨著靜力需求的降低而降低,動力響應進一步降低,起到良性循環的作用。

需要指出的是,本文僅對該體系的有效性進行了初步研究,其他問題如撐架選型、地震響應系統分析將在下階段工作中進行研究。