GeoGebra輔助線性規劃教學實踐研究

◇宿遷職業技術學院 王榮亮

線性規劃課程具有較強的實踐背景，對數形結合有較高的要求，學生普遍感覺求解枯燥無味。如何利用現代化手段，提高線性規劃教學，提升學生的興趣，促進教學質量更進一步，是職業院校數學教學須面對的一個問題。結合具體案例，討論了GeoGebra在線性規劃教學過程中的應用和實踐效果。結果表明：GeoGebra的強大繪圖功能和動態呈現功能，有利于提升數學教學質量和教學效果。

線性規劃是運籌學中研究較早、發展較快、方法較為成熟、應用也較為廣泛的一個重要分支。線性規劃主要研究如何將有限資源的進行最佳分配，即如何對有限的資源作出最佳的配置和最有利的使用，以便最充分的發揮資源的效能去獲得最佳的經濟效益。學習線性規劃的一些基礎知識，用線性規劃方法解決一些簡單的實際問題，可以培養學生數學建模意識和動手能力，提升學生對“數形結合”思想的理解與應用，這對于職校學生是必要的。同時，職校學生基礎相對薄弱，自主學習能力不強以及線性規劃知識本身對圖形繪制和求解過程可呈現性不強等特點給職校線性規劃教學帶來了極大的挑戰。

顯而易見的是，數學可視化教學有利于知識呈現、學生接受和師生互動。楊海麗[1]指出可視化方式主要有文本表格、圖式和視頻等；廖彩云[2]將可視化工具分為外在表征工具和心理表征工具，其中心理表征工具包括背景、故事、模擬實驗等通用工具和數學史、數學實驗等專門工具；司業佳[3]借助GeoGebra構造了輔助函數教學三個案例，有助于學生概念理解。周后卿、徐幼專[4]將MATLAB引入復變函數教學，通過大量的代碼，實現了復變函數可視化教學，促進學生對知識的深入理解；李昌志等人[5]運用MATLAB和幾何畫板構建了函數和幾何兩個模塊的教學案例，提升課堂趣味性，引起學生的興趣，提高課堂效率；努爾色曼·買買提[6]編寫了相對應代碼，展示了MATLAB在函數及其極限中的應用；高芹[7]將GeoGebra貫徹在備課設計、課上設計和測試反饋三個環節，對中職課堂教學優化顯著；王潔丹[8]利用GeoGebra對數學概念教學進行深化設計；張茜[9]將MATLAB應用到高等數學原理探究、數值計算和數學三大模塊，提升了學生學習效果；袁蘭蘭[10]利用GeoGebra進行數學問題、數學猜想和數學概念可視化設計，更利于學生理解概念，實現知識遷移。韋美成[11]指出GeoGebra具有功能齊全、操作方便、動態交互、易安裝、網上直接使用等優點，也開展了數學教學探究，顯著提高了學生的及格率、優秀率。

可見，MATLAB輔助數學教學可視化對編程要求較高，而GeoGebra具有交互性能，更易于操作。采用GeoGebra輔助教學，呈現尋找線性規劃問題中最優解的動態過程，可深化學生對線性規劃問題的認識，使學生對線性規劃理解更直觀、更深刻，進一步體會“數形結合”思想。本文通過三個案例展示了GeoGebra輔助線性規劃的教學，凸顯了GeoGebra的動態功能在教學中的重要作用，為線性規劃教學提供一種思路和參考。

1 設計原則

1.1 注重應用性

線性規劃最大的特點就是具有廣泛的應用性。注重線性規劃教學的應用性，有利于培養學生應用數學解決實際問題的能力和素養。在進行線性規劃教學可視化設計過程中，秉持數學教學貼近生活的教學理念，充分考慮線性規劃的應用性，列舉一些生活中常見的問題，通過數學建模方法，將這些實際問題抽象為一般數學表達式，即建立線性規劃模型，求出對應的最優解。

1.2 體現直觀性

線性規劃問題的求解往往涉及圖像法、表格法等，對學生幾何繪畫能力和動態思維提出了較高的要求。在進行線性規劃教學可視化設計過程中，應該充分考慮采取何種方式來呈現線性規劃求解的動態化要求，讓學生直觀感受到求解過程的動態性，理解線性規劃如何動態過程中尋找最優解及尋找最優解的本質。

1.3 突出主體性

在教學可視化設計過程中要突出學生主體性的原則。興趣是學習最好的動力，影響學生獲得正常學習成就的最主要原因就是學生對所學知識沒有興趣。突出學生主體性，就是在教學可視化設計過程中讓學生參與教學，與學生產生互動，將課堂交還學生，營造一個學生主動參與、獨立思考的環境，培養學生學習知識的興趣。

1.4 強調可操作性

可操作性原則是保證設計的案例能被教師移植、學生參與的一個重要原則。在教學可視化設計過程中，要在保證邏輯性和正確性的基礎上，充分考慮案例是否能被其他教師所用，是否易于學生接受并參與操作。

2 可視化案例

線性規劃教學一般通過列舉一些常見的實際問題，通過數學建模方法建立線性規劃模型，引入決策變量、目標函數和約束條件等部分。再介紹如何通過圖像法求解二元線性規劃問題。概念教學是基礎，注重數學建模過程。圖像法求解是重點，注重培養學生數形結合思想。利用GeoGebra輔助線性規劃教學，通過文字呈現、圖片導入和動態演示等，更有利于培養學生分析問題能力，更具體展示求解過程。

（1）線性規劃問題概念教學。

在引入線性規劃中的一些基本概念的教學可視化設計中，主要選擇了四種常見的類型：產品安排問題、物資調運問題、下料問題和人力調配。具體的過程主要包括問題導入、建模過程、數學表達式和基本概念四個部分。

點擊“問題導入”按鈕，將通過文字呈現需要探究問題的實際背景，如圖1所示。

點擊“建模過程”，將一步步引導學生按照探究問題的要求建立對應的方程，如圖2所示。

當建模過程完成后，點擊“數學表達式”按鈕，將建模過程中建立的方程進行重新書寫，轉換成數學表達式，如圖3所示。

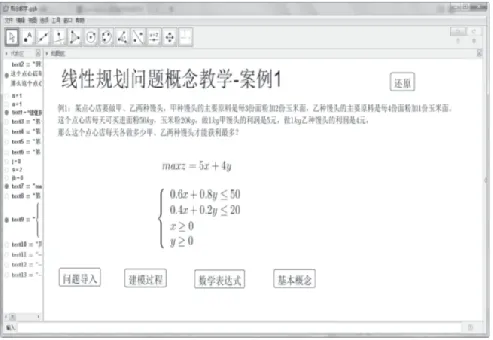
圖3 數學表達式

點擊“基本概念”按鈕，將對前面的數學表達式各個部分進行概念化，如圖4所示。

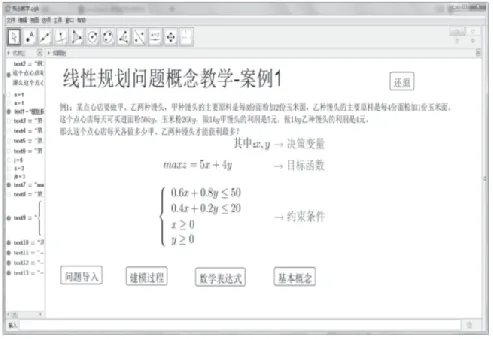
圖4 基本概念

（2）圖解法求解案例。

圖解法是求解二元線性規劃問題最為基本的一種方法。圖解法首先要確定可行域，然后通過平移目標函數尋求最大值。

進行可行域教學時，采用類似如圖5所示的可視化案例。主要步驟如下：①在平面內畫一條直線，如x-3y-4=0；②在平面內取一點A，并將點A的x坐標和y坐標帶入x-3y-4中，判斷與0的關系；③移動點A的位置，觀察x-3y-4與0關系的變化情況；

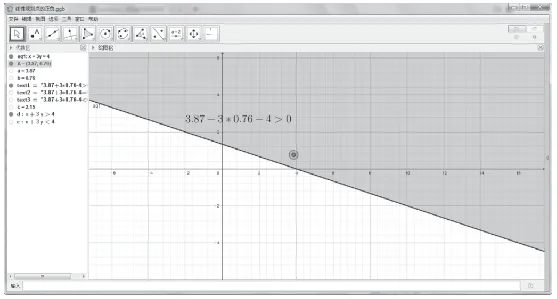
圖5 可行域案例

通過移動點A的位置，學生可清晰的發現直線x-3y-4=0將平面分為三個區域：x-3y-4>0、x-3y-4=0和x-3y-4<0。同時，學生可用操作軟件更改直線的方程，繼續觀察即使直線方程不一樣，但是直線都可以把平面區域分割為三個部分，故而在實際操作中可以通過特殊點是否滿足不等式來確定可行域。

進行二元線性規劃問題的圖解法教學時，主要采用類似如圖6的可視化案的步驟如下：①在平面內畫出符合條件的可行域，如；②在①確定的可行域內取一點A，并將點A的x坐標和y坐標帶入2x+3y，并求出其值；③移動點A的位置，觀察2x+3y值變化情況，可以發現在（4,2）點處取得最大值。

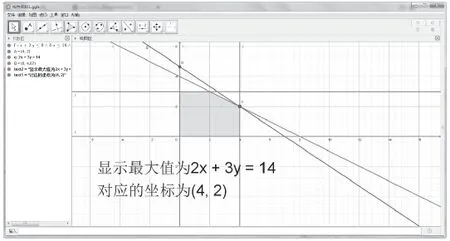
圖6 二元線性規劃求解案例

通過移動A的位置，可以觀察到過A的一系列斜率相同的直線在y軸上的截距是不斷變化的，并且在（4,2）處截距最大，而此時2x+3y也取得最大值。這也進一步解釋了在實際過程中往往將目標函數處理成斜率相同的直線，然后不斷進行平移，觀察直線在y軸上的截距變化情況，再確定目標函數取得最值的點。

3 實踐效果分析

為了檢驗GeoGebra輔助線性規劃教學的有效性，討論該軟件是否可以提升學生對數學的興趣，增強學生學習數學的動力，選取了宿遷科技學校兩個平行班，一個為實驗班，一個為對照班。實驗班的教師采用GeoGebra輔助線性規劃教學，對照班主要采用黑板進行講解線性規劃的知識。

對比兩個班級學習線性規劃前后的兩次月考成績，如表1所示。兩個班級在實驗前成績沒有顯著差異，但是經過實驗過后可以發現實驗班相對對照班成績有較大差異。這說明GeoGebra輔助數學教學相較于傳統的板書式教學更有利于學生對知識的掌握。

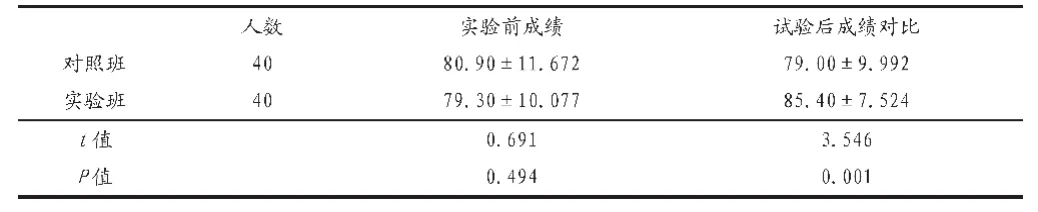
表1 兩個班級學習線性規劃前后的兩次月考成績的對比

對實驗班40名學生進行問卷調查，問卷內容包括2個主題，6個選擇題，回收有效問卷40份，統計分析的結果如表2所示。調查結果顯示100%的學生希望使用GeoGebra輔助線性規劃教學，100%的學生認為在線性規劃教學過程中GeoGebra使用可以提高學習興趣，87.5%的學生認為GeoGebra使用有助于專注度的提升，95%的學生認為GeoGebra的動態呈現功能可以幫助對概念的理解，97.5%學生認可GeoGebra的互動性并認為這樣可以提升學生的探究能力，87.5%的學生認為GeoGebra的使用可以降低知識難度。

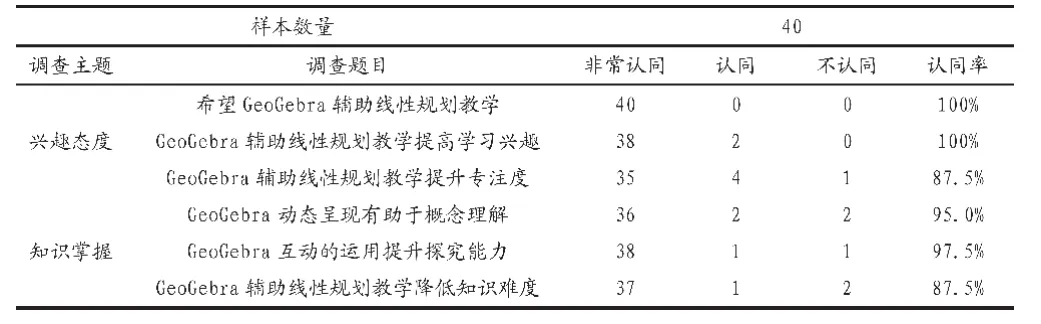
表2 GeoGebra輔助數學教學效果分析

綜上，GeoGebra輔助線性規劃教學有助于學生對概念的理解和知識的掌握，提高學生學習數學的興趣。

4 結束語

線性規劃是職業院校數學課程中比較重要的知識點，對數形結合要求較高，在教學過程中應理論性和實踐性相結合。GeoGebra強大的繪圖功能和動態呈現功能，有助于數學教學的可視化，降低知識難度，幫助學生更好的理解概念，提升學生對數學的興趣，培養學生的探究能力。在職業院校數學教學實踐過程中，應當不斷拓展其應用，更好的提高教學質量。