解題研究:從解法研究走向解題教學設計
秦延延














[摘? 要] 針對中考較難題,教師往往不只局限在答案獲取上,還會關注回顧反思階段的一題多解與模式識別. 當然,更重要的是,要從解法的深度思考走向解題教學的精心預設. 包括預設出較難題的鋪墊問題、引例問題、簡化問題、等價問題、拓展問題等,再根據由易到難的方式漸次呈現,促進學生在解題學習中學會思考.
[關鍵詞] 解題研究;自貢中考;深度思考;解題教學設計
每年中考試卷“新鮮出爐”之后,在一些自媒體公眾號、“解題群”都能看到不少教師的解題熱情,其中一題多解、巧思妙解、無字解法等“熱度很高”.然而,解題研究還需要從“一題多解”走向“多解歸一”,更需要從解法研究走向解題教學研究. 本文以一道2023年中考較難題為例,整理該題的解法思路與解題教學微設計,并進行反思.
由一道中考題的思路突破及解后反思說起
考題? (2013年四川省自貢市中考題)如圖1所示,分別經過原點O和點A(4,0)的動直線a,b的夾角∠OBA=30°,M是OB的中點,連接AM,則sin∠OAM的最大值是(? ? )
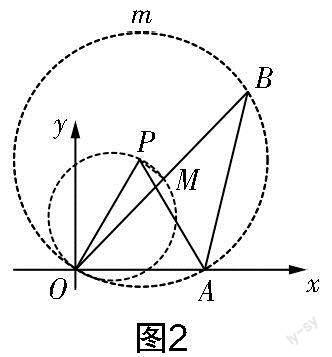
思路突破:觀察△AOB,由已知條件可知OA為定長4,它所對的∠OBA是定角30°,于是可聯想到“定弦定角”的解題經驗,所以構造如圖2所示的圓P(以OA為一邊在第一象限取點P,構造等邊三角形AOP,再以點P為圓心,PO的長為半徑畫出圓P,點B的軌跡是優弧OmA,不包括端點O,A). 接著思考OB中點M的軌跡. 如圖2所示,連接PM,在大圓中由垂徑定理得PM⊥OB,由此有∠PMO=90°,結合OP是定長,可知點M的軌跡是以OP為直徑的圓的一段圓弧.接下來我們適當刪除圖2中的一些線條,得到如圖3所示的“簡化”圖形,進一步研究∠OAM何時取得最大值.
在圖3中,點A是☉Q外一點,過點A作☉Q的切線AM(切點M在第一象限),此時∠OAM最大.
解后回顧:從上面的思路突破來看,以下兩個“關鍵問題”值得重視,讓我們“提取”分析如下.
關鍵問題1:如圖5所示,在△AOB中,AO=4,∠B=30°,點M是邊OB的中點,分析點M的軌跡.
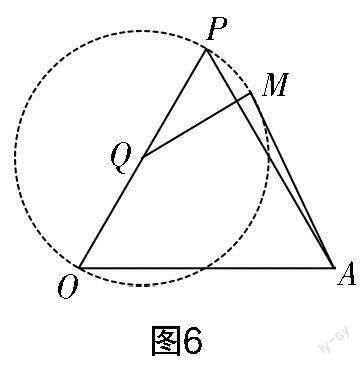
關鍵問題2:如圖6所示,OP是☉Q的直徑,點M在☉Q上,且P,M都在OA的同側,當AM與☉Q相切時,求sin∠OAM的值.
另解分析:對于“關鍵問題2”,還可以借助高中“三角公式”直接計算. 如圖7所示,連接AQ,可分別求出∠OAQ,∠MAQ的正切值,然后運用兩角和的正切公式,求出tan∠OAM的
教學環節1:基礎熱身
問題1:在△ABC中,AB=4,∠ACB=30°.
(1)當AC=BC時,求△ABC的面積.
(2)小明發現(1)中的情形,使得△ABC的面積取得了最大值. 你同意小明的發現嗎?請說明理由.
教學預設:第(1)問是“特例引路”,讓學生感受到頂點C在AB邊的垂直平分線上的特殊位置.而要解釋第(2)問,則需要作出點C的軌跡(在一段優弧上). 第(3)問根據對稱性質,如圖8所示,有兩個符合題意的點C,且都為等腰三角形. 教學時教師要請注意訓練學生思維的嚴謹性.
教學環節2:拾級而上
問題2:如圖9所示,在△ABC中,AB=4,∠ACB=30°,BD是△ABC的中線.
(1)分析中線BD的最大值與最小值;
(2)當∠ABD最大時,求中線BD的長.
教學預設:第(1)問的關鍵是
教學環節3:挑戰考題
問題3:見上文“2013年四川省自貢市中考題”,解題時可參考上文的思路突破及解后反思,限于篇幅,這里略去.
教學組織:呈現考題后,教師要先引導學生獨立思考,將問題的本質看清,再分離圖形、簡化問題,看出需要突破哪些關鍵步驟,與前面“教學環節”中已經研究的哪些問題等價,這樣就可以快速“通過”較難步驟.對于思路較快的學生,可優先讓他們講解思路,再安排其他學生復述思路,讓更多的學生都想通解題的關鍵步驟. 如果課堂時間不夠,解題過程或一些細節可以留作課后進一步整理成解題筆記,而將課堂時間盡可能多地用在思路分析、關鍵步驟的突破上.
寫在后面
筆者以為,“完整”的解題研究包括解題方法或思路的深度探究,含一題多解、多解歸一、結構揭示、復雜問題或圖形的分離與簡化等;解題教學各個環節的精心設計,包括鋪墊問題的預設、變式問題漸次呈現、較難題的思路啟示等預設.而以上這些,都離不開教師持續修煉與精進命題改編的專業基本功.

