多維聯(lián)想 多方探究
范建兵







[摘? 要] 文章通過一道中考壓軸題的深度剖析,引導師生在解題教學中關注知識融合和圖形解構(gòu),多維聯(lián)想尋思路,多方探究求生長.
[關鍵詞] 聯(lián)想;突破;探究
試題呈現(xiàn)
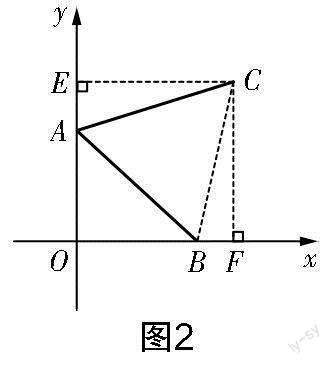
試題 (2022年江蘇省蘇州市中考數(shù)學卷第8題)如圖1所示,點A的坐標為(0,2),點B是x軸正半軸上一點,將線段AB繞點A按逆時針方向旋轉(zhuǎn)60°后得到線段AC.若點C的坐標為(m,3),則m的值為( ? ? )
解法探究
解題教學是數(shù)學教學中一種基本的教學方式,又是培養(yǎng)學生理解數(shù)學、思考數(shù)學的基本途徑.本題設計巧妙,基于課本又高于課本,借助圖形的旋轉(zhuǎn),融合了等邊三角形、直角三角形、勾股定理、相似等幾何知識,為學生提供了施展才華的廣闊空間. 現(xiàn)提出幾種解題思路,供大家參考.
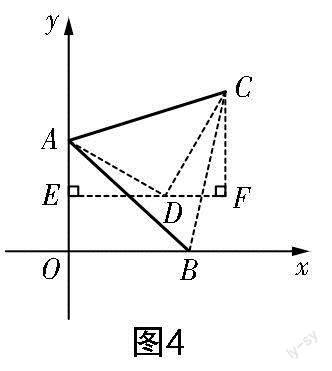
思路3 如圖4所示,將線段AO繞點A按逆時針方向旋轉(zhuǎn)60°后得到線段AD,過點D作DE⊥y軸,交y軸于點E,過點C作CF⊥ED,交直線ED于點F. 根據(jù)旋轉(zhuǎn)可得△AED各邊的長,再由“一線三直角”模型可得△AED∽△DFC,接著根據(jù)相似三角形對應邊成比例且CF=2,求得DF的長,從而求出m的值.
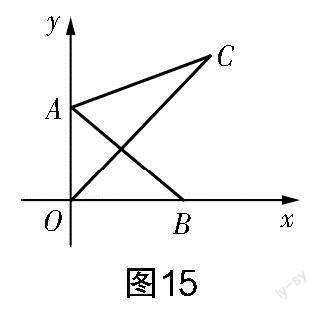
思路4 如圖5所示,過點C作CD⊥x軸,交x軸于點D,連接CB,構(gòu)造∠AEO=∠CFO=60°,先分別解Rt△AEO和Rt△CFD,再通過證明△AEB≌△BFC,得到AE=BF,EB=FC,從而建立方程并求得m的值.
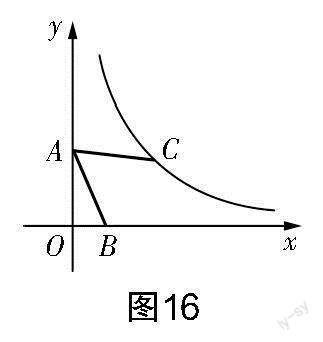
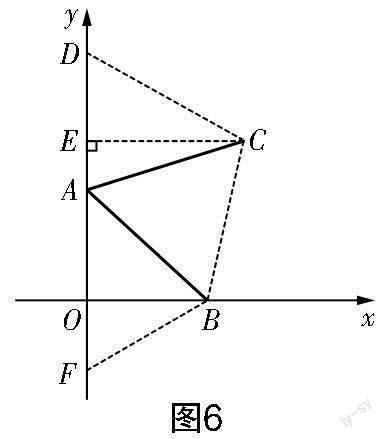
思路5 如圖6所示,與思路4相似,過點C作CE⊥y軸,交y軸于點E,連接CB,構(gòu)造∠CDE=∠BFO=60°,先分別解Rt△CDE和Rt△BFO,再通過證明△CDA≌△AFB,得到CD=AF,DA=FB,從而建立方程并求得m的值.
……
試題評價
1. 思路探尋,從條件中想關聯(lián)
G.波利亞在《怎樣解題:數(shù)學思維的新方法》一書中提醒我們:你以前見過它嗎?你是否見過形式稍有不同的類似問題?你能從已知數(shù)據(jù)中得出一些有用的東西嗎?你能以不同的方式推導這個結(jié)果嗎[1] ?這說明問題的解決離不開聯(lián)想,聯(lián)想能夠幫助我們有效地、快速地探尋到解題思路.
蘇州前幾年的中考幾何綜合題,往往涉及許多知識點,并且有著較難的圖形識別要求.2022年第8題一改“常態(tài)”,以最基礎、最簡潔的幾何圖形(線段)為載體,考查了學生對幾何變換(旋轉(zhuǎn))的理解. 題目看似簡單,但簡單圖形中卻蘊含了豐富的思維要求,對學生的幾何直觀、抽象意識、應用意識等素養(yǎng)要求很高. 解題時,我們不妨將試題中的各類知識串聯(lián)起來,通過知識的整體性與關聯(lián)性展開聯(lián)想,尋找可能的解題思路. 如由“旋轉(zhuǎn)”聯(lián)想到變換前后的變和不變,由“60°角”聯(lián)想到等邊三角形和特殊角的三角函數(shù)值,由“計算邊長”聯(lián)想到勾股定理,由“平面直角坐標系”聯(lián)想到點的對應、直線解析式、關鍵點的坐標、待定系數(shù)法等……
2. 方法探究,從經(jīng)驗中尋突破
G.波利亞將數(shù)學解題劃分為四個階段:讀題、擬訂方案、執(zhí)行、回顧[2]. 反思以上幾種思路:對于思路1,學生比較容易想到,但它對學生的運算能力要求太高,許多學生看到方程時望而卻步,無法順利求解;思路2和思路3的思考源于對旋轉(zhuǎn)的深度理解,特別是在平面直角坐標系中,要求學生能將線段AB的旋轉(zhuǎn)習慣性地看成是△AOB的旋轉(zhuǎn)(這種思考問題的意識需要教師在平時的教學中不斷滲透),找出其中的定量(點D的位置和點C的軌跡)與變量(點B和點C的坐標),這樣更有利于問題的解決. 順利讀題、擬訂方案、執(zhí)行方案后,學生還需要養(yǎng)成良好的回顧與反思解題習慣,突破經(jīng)驗再思考:我是怎么想到的?還可以怎么想?哪種方法更好一些?
3. 模型識別,從解題中找思路
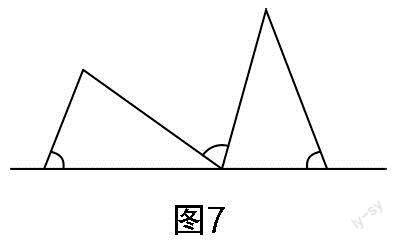
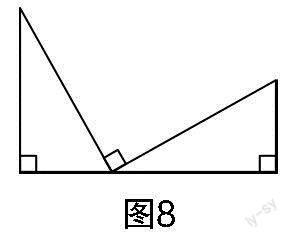
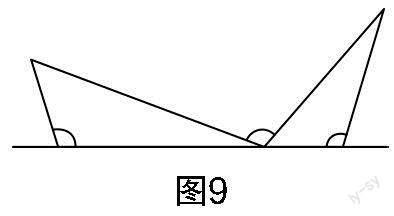
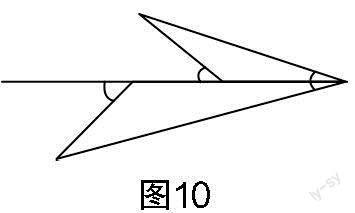
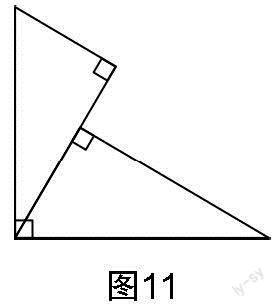
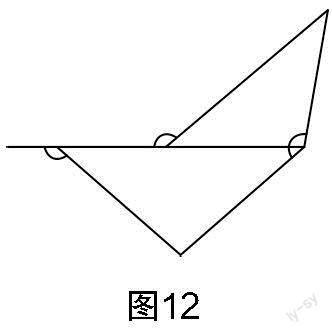
加強解題教學不是同一問題的反復訓練,更不是搞題海戰(zhàn)術(shù). 它的正確做法是通過解題和反思活動,在解題的基礎上總結(jié)、歸納解題方法,強化建模意識,提煉數(shù)學模型,提升學生素養(yǎng). 思路4和思路5都應用了“一線三等角”解題模型,借助模型來構(gòu)造圖形的全等或相似,從而建立方程并求解. 作為一個常練常考的幾何模型,“一線三等角”深受教師和學生的喜愛,在蘇科版教材八年級上冊第35頁和九年級下冊第59頁、第91頁都有明確的“一線三等角”圖例. 教學中,教師要鼓勵學生“窺一斑而知全豹”,引導學生在已有學習經(jīng)驗上不斷關聯(lián)和引申. 圖7至圖12都是“一線三等角”常見的基本圖形(可根據(jù)角度大小與相等角的分布進行分類). 因此,解題教學中增加基本圖形的識別與構(gòu)造,可以豐富學生的認知結(jié)構(gòu),完善學生的知識體系,提高學生分析問題與解決問題的能力,提升學生的模型觀念,增強學生的創(chuàng)新意識.
4. 深度探究,在反思中求生長
深度學習是在已有認知結(jié)構(gòu)上的一種完善與遞進. 在問題解決的基礎上,為了讓學生更好地理解問題的解決路徑,實現(xiàn)中考題引發(fā)思考和引領教學的潛在功能,我們可以通過對原有問題的再提問、再改編等方式對具體知識進行再建構(gòu),以引發(fā)師生深度理解,促進解題經(jīng)驗的再生長.
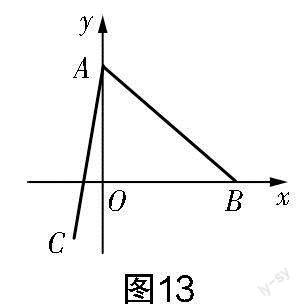
改編1 基于原題旋轉(zhuǎn)方向的改編.
如圖13所示,點A的坐標為(0,2),點B是x軸正半軸上的一點,將線段AB繞點A按順時針方向旋轉(zhuǎn)60°后得到線段AC.若點C的坐標為(m,-1),則m的值為____.
改編2 基于原題旋轉(zhuǎn)角度的改編.
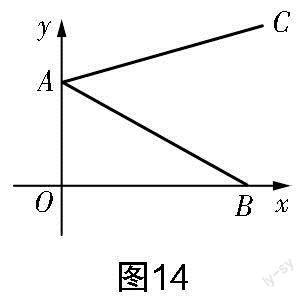
如圖14所示,點A的坐標為(0,2),點B是x軸正半軸上的一點,將線段AB繞點A按逆時針方向旋轉(zhuǎn)45°后得到線段AC.若點C的坐標為(m,3),則m的值為____.
改編3 基于原題隱含結(jié)論的再挖掘.
如圖15所示,點A的坐標為(0,2),點B是x軸上的一個動點,將線段AB繞點A按逆時針方向旋轉(zhuǎn)60°后得到線段AC,連接OC,則線段OC的最小值為____.
改編4 基于知識的再融合.
結(jié)束語
什么是好題?個人認為好題應該具備來路正、出路廣、融合強、韻味足的特征,源于課本但又高于課本,既能夠體現(xiàn)基本知識和基本技能的考查,又能夠引領學生解題能力的提高和數(shù)學素養(yǎng)的提升[2]. 2022年江蘇省蘇州市中考數(shù)學卷第8題就是好題的代表,具有圖形簡潔、構(gòu)造簡單、思路寬廣的好題之韻,讓人流連忘返、回味無窮.
參考文獻:
[1]G.波利亞. 怎樣解題:數(shù)學思維的新方法[M]. 涂泓,馮承天,譯. 上海:上海科技教育出版社,2011.
[2]陳偉華. 認清“來路”? ?認準“出路”——以2020年蘇州市中考數(shù)學卷第18題為例[J]. 中學數(shù)學雜志,2021(10):53-54.

