從通法到通性：追求解題的自然屬性

姚春珍

［摘? 要］ 中考復習需注重思維的發生過程，要從通法到通性，追求解題的自然屬性. 教師進行中考復習時，要通過試題演練，使所有學生有不同的發展，要通過理思路、探方法來找到通法，從善總結、悟方法過渡到通性，最后深化到提升能力，從而提高復習的實效性.

［關鍵詞］ 中考試題；自然屬性；通法通性；復習實效性

目前，不斷有研究“自然解法”的文章出現，但大都基于解題學微觀層面探討自然“通法”，缺乏對解題學教學論的中觀研究. 而中考數學試題作為解題學的主導方向，對課堂教學起著“自然性”思想統領作用，因此，立足于系統常規研究試題的“通性”維度更具有前瞻意義.

就存在哲學范疇而言，“自然”取自然而然之意，即按照事物內部規律而發展變化. 北京林業大學王向榮教授認為，自然性包括原始的自然、生產的自然和美學的自然. 把自然界的這種自然性借用到教學論領域，則需要追求解題的自然屬性［1］. 下面以2019年蘇州市中考數學試題第25題為載體，呈現解題探究的自然性，凸顯“崇尚自然和常規”的自然要義，引導自然課堂素養教育的實踐行為.

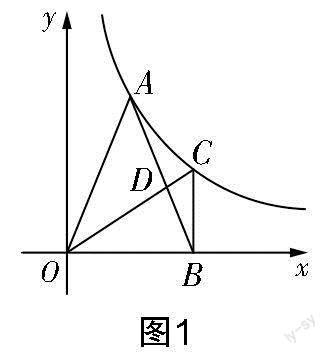
試題呈現

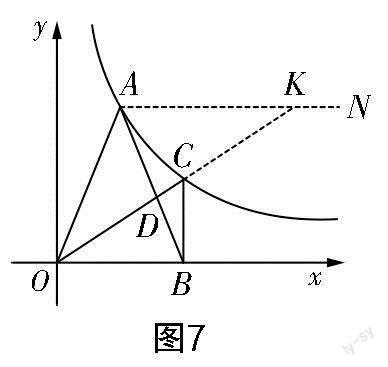
本題重點考查反比例函數、等腰三角形、勾股定理以及相似等知識. 本題為學生提供了綜合知識抒發見解的學習窗口，學生可以從已有的經驗出發，將學習的知識概括成問題，然后創設出與認知相沖突的問題，接下來為解決沖突而繼續深究，從而使問題重新明朗化. 在以此題為線復習函數中檔題的過程中，筆者發現學生對于第（2）問的求解方法有多種，這體現了學生在初中階段學會了用不同的思維方式思考問題，用不同的方法攻破問題，會綜合運用數學知識解決問題，體現了學生的應用意識和創新意識. 此題既體現了初中數學教學知識的著落點——從通法到通性，找到解題的自然屬性，又彰顯了核心素養在初中數學這塊知識土地上落地生根，培養了學生的實踐能力［2］.

解法探究

1. 找尋常規思路，剖析圖形本質，實現自然回歸

尋求常規解題思路，需要溯源比較. 溯源比較是解題的基本維度，反映解題學系統內部的自然屬性. 這里的“溯源”是對問題來源的哲學追問；“比較”是對研究方法的認證，帶有定量分析到定性把握的自然特征. 這就是齊民友先生所認為的解題要“回到自然”，而“回到固有的生動活潑的思考”也是克萊因大師的數學遺風. 因為生動活潑思考心理狀態是溯源比較的意義結果［3］，可見自然屬性包括溯源比較的本體特征，是自然解題教學論的起點.

教材上的練習題綜合考查了相似三角形的判定與性質、線段的中點、分數的基本性質等知識，要求學生重點掌握相似三角形的判定與性質. 學生探究出“相似三角形對應中線的比等于相似比”后解決此題便比較容易上手. 教師上課講解時可加入變式，目的在于讓學生掌握求解的自然屬性. 前面的中考題與教材上的練習題，圖形本質是相同的，因此學生很容易想到用相似三角形的性質來求解中考題第（2）問.

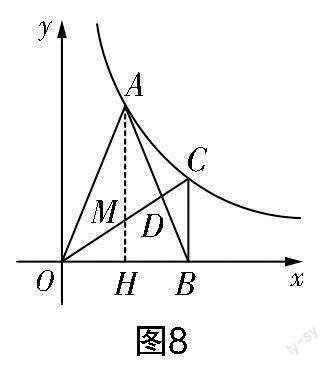
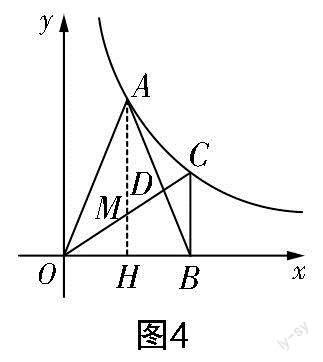
如圖4所示，過點A作AH⊥x軸，垂足為H，AH交OC于點M. 因為BC⊥

本題考查了學生的知識技能、數學思考能力及問題解決能力，運用此種解法求解的學生，說明他們的數學基礎知識扎實，基本技能達成度較好.

從問題溯源的角度來看一個城市（蘇州市）連續兩年考查同一個基本圖形的客觀事實，2020年的蘇州中考卷第10題、2021年的蘇州中考卷第24題均為一次函數、反比例函數的綜合運用，因此研究解題的自然屬性為試題研發提供了方向和趨勢，敞亮地呈現了試題的來龍去脈和立意關聯，反映了命題本源的自然屬性，揭示了比較研究的意義在于發散思維的自然過渡，從而實現試題的自然回歸.

2. 巧添輔助線，轉化比值，實現自然聯想

解題過程中學生應綜合運用數學知識. 知識點在教材中是靜態呈現的，但在解題運用中是動態生成的. 在復習階段，教師應從整體上把握教學內容，讓學生從知識結構上將內容進行整合，將知識進行統籌，將方法進行內化，從而實現解題的自然聯想. 添加輔助線，是學生運用所學知識解題時質的飛躍的體現. 復習階段，教師應遵循量力性原則，讓學生感悟數學知識的關聯性、整體性，從而實現自然聯想，實現自然解題的發展.

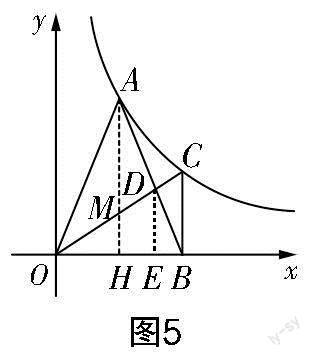
解法二：學生在解得C（4，3）后，并沒有直接求出交點M的坐標，而是運用“平行線等分線段定理”求線段MH的長度或轉化成線段的比來求MH的長度.

學生把求線段AM長度的解決思路和方法進行了遷移，不是中規中矩地運用常規方法，而是另辟蹊徑，讓計算量相對減小. 有的學生解得點D的坐標后，過點D作x軸的垂線，運用“平行線分線段成比例定理”將比例進行轉化. 學生解得點D的坐標后，想到求比值用相似比，于是回到出發點. 在作高的過程中，學生得到比例的性質，可謂“植一木，成一林”. 解題中體現了用幾何直觀和空間想象來理解數學，更體現了學生將知識轉化為能力.

從自然屬性出發，在從“解決什么”到“學到什么程度”的過程中，研究解題的自然聯想為解決此類問題指明方向，提示“轉化”思想，過渡到自然聯想. 此類解法使學生學會思考，解題穩重而又不失方法靈活. 學生基礎知識和基本技能達到一定程度時才能得到自然聯想，上述求解過程充分體現了學生分析問題和解決問題的能力，學生的推理能力和幾何直觀等核心素養培養也落到了實處.

3. 借助相似三角形，尋求通法通性，實現自然建模

學生在尋求更高層次的解題思路時，會經歷綜合運用知識的過程，掌握解題方法，拓寬研究問題的思路，會有新的認識，新的生成，新的思維突破，并形成通法通性，實現自然建模，最終培養學生的基本素養. 學生求線段的長度時，借助相似三角形構造模型，可見自然屬性應包括通法通性的特征，實現自然建模，實現自然解題教學論的飛躍.

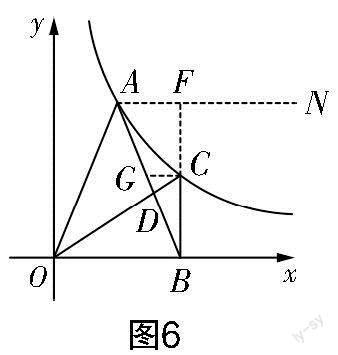
解法三：學生發散思維，在AB的右側構造“A”形相似三角形，使計算量減小.

學生通過兩次構造相似三角形來求解，即在AB右側構造圖形，使計算簡單，將問題轉化為一個合適的數學模型，體現了學生對相似三角形知識有較強的綜合運用能力. 此解法培養了學生的發散思維，并通過問題重新構造模型，體現了學生的數學建模素養.

解法四：學生通過構造“X”形模型找相似.

學生的思維非常活躍，為找相似，順其自然地想到了構造“X”形相似. 由數到形，培養了學生的空間想象能力和抽象思維能力. 學生采用上述解法，說明學生平常學習中注重實踐探究，體現了學生思維的廣闊性和靈活性，更體現了學生的想象能力很強，數學建模也搭建得比較成熟.

從問題通法通性角度解答此類中考題，從題目的適宜性、生成性、創生性角度出發評析此類題目，此題難度不大，兼顧了所有學生，讓學生都有所體悟，因此起到了“以題知法”的作用. 此題可以作為數學復習階段的原始素材，然后延伸教學內容，拓寬思維，尋求通法通性，實現自然建模，最終得到試題的自然回歸.

4. 借助參數，由特殊到一般，實現自然順應

尋求解題的一般性思路，能真正掌握數學知識內在聯系和本質特征，積累數學學習經驗，最終得到自然順應. 數學知識的獲得不能局限于某一個點，應從解決問題背后隱藏的思想方法中挖掘，內化為方法，用這種方法去研究和解決新問題，從而使問題螺旋式上升，方法螺旋式升華［4］. 可見自然屬性應包括一般性原則，實現自然順應，實現自然解題教學論的升華.

解法五：有少量學生將點A看成動點，運用參數k來解決問題.

此解法與解法三有相同之處，但繞開了k的具體數據. 可以說在如此短的時間內將數學“從特殊到一般”思想達到融會貫通的地步，是學生“學習能量”和核心素養積累到一定程度才能達到的境界，其能為學生的創新意識培養和可持續發展奠定基礎.

從問題一般性原則出發講述同一知識考查的客觀內容，從“特殊到一般”的數學思想蘊含數學的一般性觀念，能提升對知識點和方法的深度理解，將方法內化于心，將數學思想轉化為數學策略，從而實現自然順應，實現知識的自然屬性回歸.

教學啟示

中考真題作為復習階段的原始素材，有重要的引領作用，教師如何在課堂分析中進行客觀呈現，如何將解題的自然屬性進行呈現，如何將試題的通性進行體現都非常重要，真題講解將引領課堂自然生成.

1. 理思路，探方法

教師的作用在于提升學生的認知高度，復習的任務還在于“發展”，即知識得到新的發展，學生得到新的發展. 很多試題，表面上看是新題，但同舊題的求解方法差不多. 這打破了教師和學生的慣性思維，促使師生共同探索，教學相長，其樂無窮.

2. 找通性，善總結

復習的任務在于系統整理、融會貫通. 上述試題喚醒了學生已有的解決函數的經驗，運用構圖直接求解或運用轉化等方法，都是找通性，讓零散的知識一一再現. 上述過程，學生通過解題，將原有的知識點形成系統的知識網和思維網，從“找模型—建模型—解模型—用模型”的通性中去解決問題，并總結經驗. 解題復習，能增強學生對數、形的整體認識，能使知識達到系統性、連貫性和可持續性，同時有利于將學生從茫茫題海中解脫出來，達到事半功倍的學習效果.

3. 悟方法，提能力

函數中考題一般從基本圖形出發，轉化為求交點問題、相似三角形，最后得到一個簡單的模型. 這體現了數學中從特殊到一般的數學思想方法，能促進學生把問題想深想透，將思維與實踐引向更深遠處.

在平時的復習教學中，教師不僅要關注問題的解決，要教給學生解決問題的各種方法和策略，更要注重學生數學核心素養的落實和提高. 在平時的教學中，教師要讓學生多訓練一題多解，要引導學生總結解題用到了哪些方法，是否有更特殊的解法，這些解法有沒有共同點……這樣學生就會對不同的解法進行比較，養成從不同角度思考問題的習慣，并找到此類題的通性通法. 所以，教師在平時的教學中應該多展示一些能夠鍛煉學生數學思維的真題，多滲透一些解決問題的思想，找到解題的自然屬性.

《義務教育數學課程標準（2022年版）》指出“形成重論據、有條理、合乎邏輯的思維品質，培養科學態度與理性精神”［5］，此類中考題正好呼應了新課標. 不同的學生用不同的思維解題，考查了全體學生應該達到的課程目標的基本要求，同時考查了不同學生用不同的策略. 解題教學要既面向全體學生，又關注學生的個體差異；既用常規思路，又找到通法通性，體現不同差異學生的核心素養的養成. 此類中考題將思想貫穿題中，將直觀想象、數學建模、數學運算等核心素養隱藏于解題中，找到解題的自然屬性，讓所有的學生都能參與到解題中，實現“不同的人在數學上得到不同的發展”.

參考文獻：

［1］孫朝仁. 認知系統的邏輯秩序：讓學習真正發生的“道”——基于數學實驗的視角［J］. 江蘇教育，2016（Z3）：23-26.

［2］羅增儒. 核心素養與課堂研修［J］. 中學數學教學參考，2017（23）：14-20.

［3］孫朝仁. 初中數學“教思考”的教學細化——以“分式”為例［J］. 江蘇教育，2020（91）：38-40+60.

［4］丁小將. 試析微專題在中考數學復習中的應用［J］. 數學教學通訊，2021（08）：60-61

［5］中華人民共和國教育部. 義務教育數學課程標準（2022年版）［M］. 北京：北京師范大學出版社，2022.