基于FLAC3D 的深埋隧道圍巖-支護相互作用研究
胡凱鵬
(中鐵十八局集團第五工程有限公司,天津 300450)
我國是目前世界上隧道數量最多、規模最大、工程條件最復雜、技術發展最迅速的國家。隨著隧道施工技術進步,我國由主要修建淺埋隧道逐漸向修建深埋隧道發展。與淺埋隧道僅承受地層松散土壓力不同,深埋隧道圍巖要承受地層的豎向自重應力場和水平向的構造應力場共同作用,從而產生較大的巖體變形,其形變壓力作用于支護結構,隨著巖體變形增大,其力學參數會降低,作用在支護結構上的圍巖形變壓力也會增大。當圍巖為軟巖時,達到峰值強度后的塑性變形較大,釋放其內變形能減小圍巖壓力,圍巖形變產生的壓力在二次襯砌承受的荷載中占比較大。
目前,對于深埋隧道圍巖與支護結構相互作用的研究已取得較多成果。董方庭等[1]提出隧道圍巖的松動圈支護理論和松動圈圍巖錨噴支護理論。李建軍等[2]利用FLAC3D 的Burgers 蠕變模型,分析了不同時間蠕變對圍巖應力重分布以及對二次襯砌的力學性能的影響。胡雄玉等[3]計算了考慮蠕變作用的深部地層隧道的變形及作用在隧道支護結構上的壓力,發現可利用可壓縮陶粒來減小圍巖的蠕變變形。邵珠山等[4]通過FLAC3D對隧道開挖時的受力以及變形進行計算,采用Burgers 蠕變模型對隧道的長期變形進行了模擬。我國早前修建的隧道以淺埋隧道為主,深埋軟巖隧道的實際工程較少,考慮軟巖蠕變特性的二次襯砌的受力特性與圍巖-支護結構相互作用的研究較少。鑒于此,本研究依托陜西寶漢高速公路石門隧道實際工程,通過FLAC3D 軟件進行建模與計算,對圍巖蠕變作用下的深埋軟巖隧道圍巖及支護結構的相互作用規律開展研究。
1 工程背景與數值建模
1.1 工程概況
本項目位于陜西漢中市留壩縣境內,總體地勢北高南低,主要地質地貌為黃土臺塬、黃土殘塬溝壑、河谷階地地貌,工程地質復雜,不良地質較多。石門隧道是陜西寶漢高速公路的重點控制性工程,隧道長4 350 m(雙洞),地形起伏不大,最大埋深155 m,隧址區第四系覆蓋層主要為上更新統風積物馬蘭黃土(Q3eol)、中更新統離石黃土(Q2eol)夾有薄層狀古土壤,下伏基巖為上二疊系千峰組砂巖、泥質砂巖(P2)。地表水體主要為沿線的褒河,常年流水,水量豐富,地下水分為松散巖類孔隙潛水、基巖裂隙水兩種類型,總體水文地質條件較簡單,對隧道安全無影響。
1.2 數值模型建立
1.2.1 模型基本假定
結合本次研究目的,考慮實際工程的復雜性以及FLAC3D 軟件的功能特性,在建立數值模型前對模型設置一系列的前提假定。⑴假定圍巖為各向同性的連續性介質,不考慮其各向異性的影響。⑵根據工程概況,模型不考慮地下水對隧道以及巖體力學性質的影響,力學計算參數取值均為自然含水率狀態下的巖石力學參數。⑶荷載僅考慮豎直方向的自重應力,不考慮水平方向的構造應力場影響。⑷不考慮隧道施工中的圍巖蠕變,僅考慮施工后圍巖的長期蠕變行為。⑸認為圍巖和支護結構共同變形,可以通過控制支護結構的變形來調整圍巖的能量釋放和控制圍巖壓力。
1.2.2 模型建立
基于上述假定,通過FLAC3D 軟件建立三維數值模型,為減小由邊界效應引起的計算誤差,選取模型尺寸為100 m×100 m×90 m。邊界條件設置:四周及底面約束法向位移,在模型上表面和內部單元施加模型自重應力場。
1.3 本構模型與計算參數
1.3.1 蠕變本構模型
巖體的力學特性與時間相關的性質稱為巖體的流變性,其反映了巖體的應力和應變隨時間的變化規律。蠕變指在恒定荷載條件下巖體的變形隨時間變化規律。在研究巖體的本構模型時,常將其簡化為若干基本元件再組合,盡可能精確描述巖體的力學性質。與巖體蠕變特性相關的基本力學元件有:彈性元件(H)、粘性元件(N)、塑性元件(S)。據已有研究成果,經基本力學元件的串聯和并聯,可派生15 種復合流變本構模型。
FLAC3D 蠕變分析模塊內置了8 個常用蠕變本構模型,可用來描述軟巖蠕變特性的有Burgers 模型和Cvisc 模型。Burgers 模型是Kelvin 和Maxwell體的組合,可描述土體的瞬態變形和時效變形,Cvisc 模型是Burgers 模型的M-C 準則拓展,能實現巖土體粘彈、粘性、粘塑行為模擬,Cvisc 模型在Burgers 模型基礎上,不僅可以準確描述巖體的穩定蠕變狀態,還能描述巖石的加速蠕變階段。因此選取Cvisc 模型來描述泥質砂巖的蠕變特性。
1.3.2 計算參數選取
根據假定條件,在模擬圍巖長期蠕變行為時,巖體的蠕變模型采用FLAC3D 軟件中的Cvisc 模型。根據常規單軸試驗和三軸試驗的試驗結果以及單軸壓縮蠕變試驗數據的參數反演結果,選取隧道圍巖的計算參數(見表1)。數值模型中襯砌和填充層均假定為線彈性變形材料,其力學參數見表2。

表1 圍巖數值計算參數取值
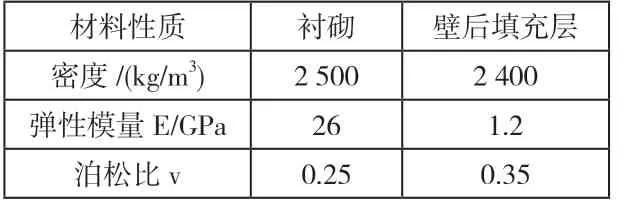
表2 結構組件的力學參數
2 蠕變作用下隧道襯砌受荷特征
建立數值分析模型并完成數值計算后,取模型縱向的中間斷面為目標面,研究其受荷特征。
2.1 襯砌變形分析
根據數值計算,得到不同時間下襯砌的豎直變形與水平變形分別見圖1、圖2。由圖1 可知,襯砌拱頂和拱底位置的豎向變形均以豎向沉降為主,隨著圍巖蠕變的發展,隧道拱頂的沉降量逐漸增大,而開挖后襯砌拱底因為卸荷作用發生隆起變形,隨后逐漸由正變為負,即隨著圍巖蠕變的發展,隆起變形逐漸減小,直至轉為沉降變形并繼續發展。由圖2 可知,在圍巖發生蠕變的不同時段,襯砌的水平變形均呈左右基本對稱,且水平變形在拱腰位置達到最大,變形向隧道外側拓展。隨著圍巖蠕變的發展,襯砌水平變形的變化不大。綜上所述,在考慮圍巖的蠕變作用后,隨著蠕變時間的延長,隧道襯砌變形整體呈現豎向沉降變形以及逐漸被壓扁的趨勢,襯砌拱頂和拱底的位移更為顯著,提取研究面的拱頂和拱底的豎向位移,得到襯砌豎向變形時程曲線如圖3 所示。
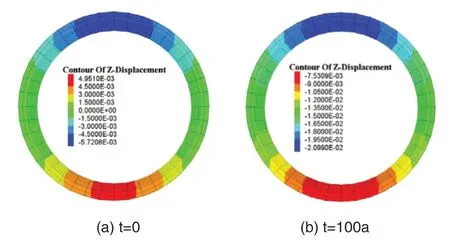
圖1 圍巖作用下襯砌豎向變形
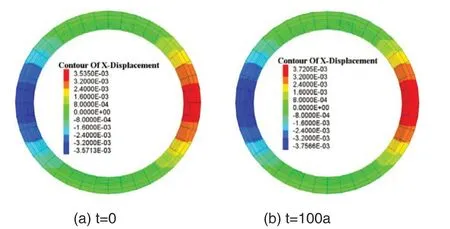
圖2 圍巖作用下襯砌水平變形
圖3 襯砌豎向變形時程曲線
由圖3 可知,模擬圍巖發生100 年蠕變過程,在考慮蠕變作用的圍巖作用下,隨著蠕變的發展,襯砌拱頂及拱底處的變形規律基本一致。表現為:襯砌在隧道開挖后的前5 年處于衰減變形階段,5 年后處于穩定變形階段。蠕變期間,拱頂的豎向變形由-5.72 mm 增至-20.99 mm,增加了266.95%,拱底的豎向變形由4.95 mm 變為-7.53 mm,增加了252.12%,而襯砌兩側水平方向的最大變形量由7.1 mm 增至7.5 mm,僅增加了約5.63%。
2.2 襯砌內力分析
根據數值計算,得到不同時間下襯砌的最小及最大主應力分別如圖4、圖5 所示。由圖4 可知,在圍巖蠕變過程中,不同蠕變時間下襯砌的最小主應力分布規律相同,基本沿水平方向和豎直方向呈軸對稱分布。最小主應力的極大值出現在拱腰內側,極小值出現在襯砌的拱頂內側和拱底內側位置,即襯砌的拱腰位置的壓應力較大。隨著蠕變時間延長,襯砌的最小主應力的極大值逐漸增大,襯砌的拱腰位置承受的壓應力逐漸增大。由圖5 可知,不同蠕變時間下襯砌的最大主應力的極值分布于拱頂和拱底位置處,即襯砌的拱頂和拱底均承受一定的拉應力。隨著蠕變時間延長,襯砌的最大主應力的極值變化不大。
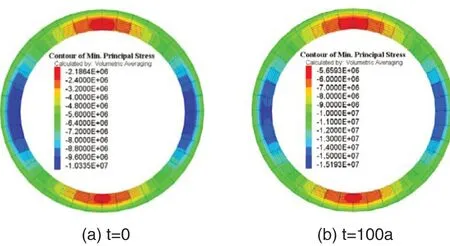
圖4 圍巖作用下襯砌的最小主應力
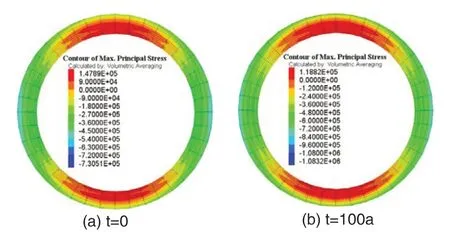
圖5 圍巖作用下襯砌的最大主應力
提取研究面襯砌的最小主應力極值,得到襯砌最小主應力極值時程曲線如圖6所示。由圖可知,在考慮蠕變作用的圍巖作用下,隨著圍巖蠕變的發展,襯砌最小主應力極值的變化為:在隧道開挖后的前5 年處于衰減階段,5 年后處于穩定變化階段,這與襯砌的豎向變形規律基本一致。
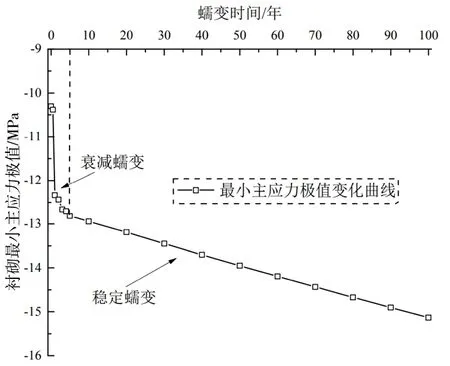
圖6 襯砌最小主應力極值時程曲線
3 埋深對結構受荷特征影響
隧道工程中,在巖體的自重應力場作用下,隨著隧道埋深增加,圍巖的地應力變大,考慮蠕變作用下,地應力越大巖體的蠕變變形越大,作用在隧道襯砌上的荷載也隨之增大,對隧道的安全產生較大危害。因此有必要研究考慮蠕變作用下隧道埋深對結構受荷特征影響,故設置6 組不同埋深條件下的數值計算工況,對應的埋深分別為60 m、80 m、100 m、120 m、150 m、200 m。
3.1 襯砌變形分析
根據數值計算不同埋深下襯砌拱頂和拱底位置的豎向變形。隨著隧道埋深的增大,拱頂位置和拱底位置的豎向變形均逐漸增大,且表現為隨著隧道埋深的增大,豎向變形后期達到穩定變形階段時的變化率越大。
3.2 襯砌內力分析
由2.2 的分析可知,不同蠕變時間下襯砌的最大主應力極值變化不大,故本節重點討論埋深條件對襯砌的最小主應力極值的影響。統計不同埋深工況下,不同蠕變時間襯砌的最小主應力極值(見表3)。
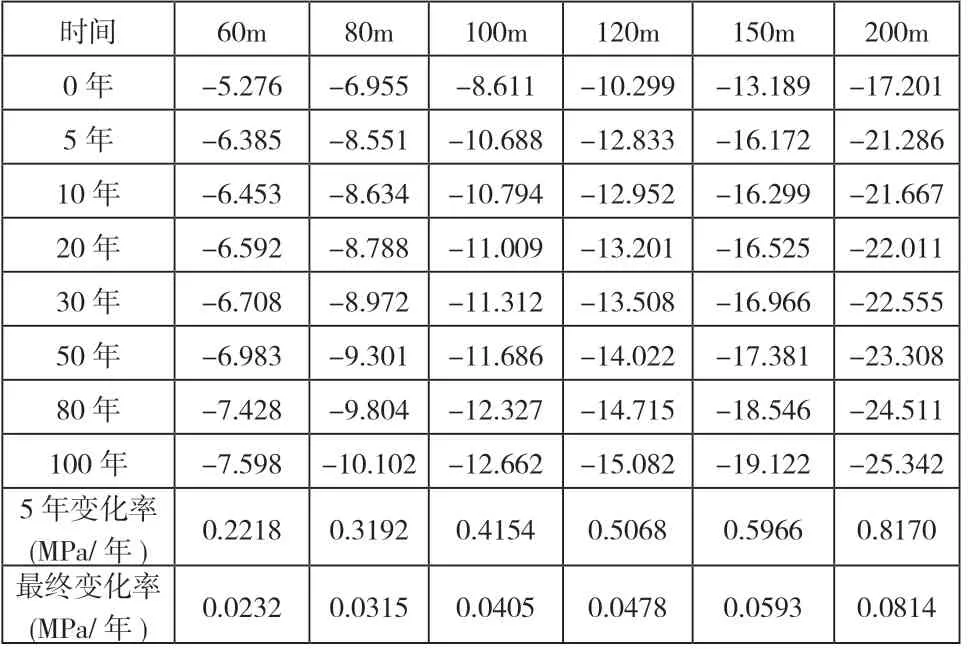
表3 不同埋深工況下襯砌的最小主應力極值(單位:MPa)
由表3 可知,隨著蠕變時間增加,襯砌最小主應力的極值也逐漸增加,從而引起襯砌結構上壓應力值增大。隨著隧道埋深增加,襯砌最小主應力的極值也逐漸增加,當埋深達到200 m、蠕變時間達100 年時,襯砌的最小主應力極值達到25.342 MPa。而隧道埋深60 m,且不考慮圍巖蠕變情況下,襯砌最小主應力極值僅為5.276 MPa,表明圍巖的蠕變作用和較大的埋深均增加了隧道運營的風險。以隧道完成修建(t=0)為起點,統計不同埋深工況下襯砌的最小主應力極值的5 年變化率和最終變化率,發現兩者均隨埋深明顯增加,隧道埋深將大大增加圍巖蠕變對隧道襯砌的影響。
4 結論
通過對圍巖蠕變作用下的深埋軟巖隧道圍巖及支護結構的相互作用規律開展研究,可知:在軟巖地層中開挖深埋隧道時,圍巖的蠕變作用對支護結構所承受荷載的大小及其分布有較大影響,在進行隧道支護結構設計時,需將圍巖蠕變作用考慮在內,防止隧道在后期運行期間出現破壞。

