低速重載風電齒輪箱徑向滑動軸承多運行狀態潤滑性能分析

趙帥可, 蘇華

(西北工業大學 機電學院, 陜西 西安 710072)

風力發電有望成為未來綠色能源的主要來源,風電齒輪箱作為風力發電設備的主要裝置,有著巨大的科研價值和市場潛力。傳統的風電齒輪箱廣泛使用滾動軸承作為傳動裝置支承,但是滾動軸承因傳遞扭矩小、承載力小、故障率高等問題無法滿足風力發電機大功率、高承載力的發展需求。因此,研制能夠滿足大傳遞扭矩、大承載力、高穩定性且制造成本低的支承系統十分迫切。與滾動軸承相比,滑動軸承具有高承載力和高穩定性的優勢,因此以滑動軸承部分取代傳統風電齒輪箱中的滾動軸承,是未來風電齒輪箱傳動系統支承的一種可行方案和研究趨勢。

由于風力和風向變化的隨機性,風電齒輪箱滑動軸承具有啟動頻繁、載荷大小和方向多變、低速重載等運行特點。

頻繁啟停和變載使得軸承更容易發生破膜,因此研究啟動工況下風電齒輪箱中徑向滑動軸承的潤滑特性十分重要。國內外已有不少學者開展了徑向滑動軸承啟動過程中潤滑性能的研究,如Liang等[1]將歐拉方程、平均Reynolds方程耦合起來,建立了水潤滑徑向滑動軸承啟動模型,研究了沖擊載荷對于軸承系統穩定性的影響;Chen等[2]將非理想軸頸的瞬態混合潤滑模型與軸頸運動方程耦合,研究了水潤滑軸承啟動過程中軸頸缺陷對其摩擦動力學行為的影響;Li等[3]通過試驗的方法測得了不同工況下滑動軸承的摩擦因數和磨損量,并指出啟動工況下軸承的磨損量和摩擦因數遠大于穩態工況;Cui等[4]研究了不同表面粗糙度對軸頸中心瞬態運動、瞬態平均油膜厚度、動水壓力和接觸壓力的影響,指出表面粗糙度對軸承啟動初期的瞬態特性有重要影響。

風電機組的服役工況比較惡劣,常年在低速、重載的工況下運行,較難形成穩定的動壓油膜,頻繁的變載沖擊會使滑動軸承中的油膜容易發生破裂造成軸徑/軸瓦粗糙表面接觸,且偏航力矩所造成的軸頸傾斜也會對滑動軸承的性能產生較大影響。因此研究風電齒輪箱中的徑向滑動軸承性能時,還必須綜合考慮表面粗糙效應、軸頸傾斜以及轉速等變化對軸承性能的影響。目前,國內外很多學者對考慮粗糙表面和軸頸傾斜的徑向滑動軸承開展了相關研究。如Sun等[5-6]通過理論和試驗的方法研究了粗糙表面滑動軸承在軸頸受載傾斜時的潤滑性能,指出在滑動軸承設計中應考慮軸頸變形傾斜所產生的影響;Sander等[7]基于平均Reynolds方程研究了徑向滑動軸承從流體動力潤滑狀態到混合潤滑狀態下的摩擦行為,通過2種不同靜載荷的摩擦試驗,指出了表面粗糙度對微凸體接觸和摩擦力矩的影響不可忽視;李彪等[8]基于平均Reynolds方程,建立了考慮粗糙表面徑向滑動軸承潤滑模型,探究了滑動軸承中表面形貌和軸頸傾斜對軸承潤滑特性的影響規律,指出在對軸承潤滑性能分析時不能忽略表面形貌的影響。上述研究一般僅考慮了穩態條件下的軸承性能,很少涉及啟動等瞬態階段。

可以看出,目前針對瞬態或穩態條件下的滑動軸承性能研究基本上是各自獨立進行的,瞬態和穩態耦合的相關研究鮮有報道。但是對于風電齒輪箱滑動軸承而言,頻繁的啟動和多變載荷工況下的性能穩定性必須同時考慮。本文基于平均Reynolds方程,提出一種將滑動軸承啟動瞬態潤滑工況和穩態潤滑工況耦合起來的性能分析方法,分析由啟動階段至穩態工況的軸心運動軌跡以及不同作用角下軸承潤滑油膜厚度、承載力的分布情況;研究表面粗糙度、軸頸傾斜角度和軸頸轉速對啟動階段和穩態工況下滑動軸承潤滑性能參數的影響,以獲得風電齒輪箱滑動軸承從啟動至穩定運行的整體運行潤滑特征。

1 幾何模型

本文研究的風電齒輪箱滑動軸承結構如圖1所示,在偏航力矩作用下軸頸會發生傾斜。其中,γ為軸頸傾斜角度;L為軸承寬度;R為軸承半徑;r為軸頸半徑;δ為外載荷作用角;c1為軸頸在軸承左端面時的中心;c2為軸頸在軸承右端面時的中心。

圖1 軸頸傾斜示意圖

本文徑向滑動軸承的結構及工況參數如表1所示。

表1 徑向滑動軸承結構及工況參數

2 數值分析方法

2.1 數值計算模型

1) 潤滑油膜厚度[9]

滑動軸承內任一點油膜厚度h為

(1)

式中:e為偏心距(不同y方向截面處偏心距不同,傾斜角度由x,y坐標進行控制);θ為軸承周向坐標;φ為作用角;c為半徑間隙;x為軸頸中心在y方向(軸向方向)不同位置的坐標值(x1,x2分別為軸承左右端面坐標值);z為軸頸中心在y方向(軸向方向)不同位置的坐標值(z1,z2分別為軸承左右端面坐標值)。

2) 平均Reynolds方程[10]

本文基于平均Reynolds方程計算油膜壓力

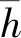
求解時采用以下邊界條件:

端泄面處:p(θ,0)=p(θ,L)=0

油膜壓力起始點:p(θ,y)=0

3) 能量方程[11]

設本文所研究的滑動軸承為均勻、各向同性材料,其導熱系數、比熱、密度均為常數,系統內無熱源,可采用能量方程

(4)

式中:ρ為潤滑油密度;cρ為潤滑油比熱;T為溫度;U為流體在x方向上的速度分量;k為潤滑油熱傳導系數;p為壓力;J為熱功當量;qx為x方向的流量;qy為y方向的流量。

能量方程的邊界條件為:

溫度起始點:T|θ=0=T|θ=2π

4) 溫黏方程

對于重載和流體動壓潤滑,本文采用更加準確的Roelands表達式[12]來考慮溫度和壓力變化對黏度的影響

η=η0exp{(lnη0+9.67)·

(5)

式中:η0為潤滑油在初始溫度T0時的黏度。

5) 微凸體接觸模型

對于油膜潤滑,在考慮干摩擦接觸時通過高斯積分得到接觸壓力與表面粗糙度因素的關系方程式[13]為

(6)

式中

表面粗糙度因素在粗糙度接觸區和全潤滑區的取值不同:

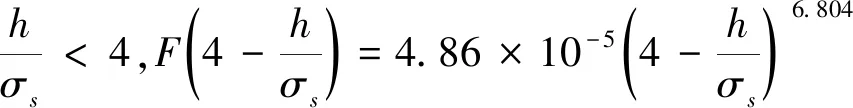
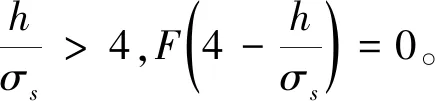
2.2 軸承潤滑性能參數計算

1) 油膜承載力[14]

(7)

(8)

(9)

Fx,Fz為油膜反力F在x和z坐標軸方向上的分量,R為徑向滑動軸承半徑。

2) 摩擦力與摩擦因數[15]

式中:Fj為軸頸表面摩擦力;uj為軸頸表面摩擦因數。

3) 微凸體承載比[16]

本文所研究的微凸體不涉及彈性變形,對于微凸體承載比的計算如(12)式所示

F′為微凸體總承載力;Ro為微凸體承載比。

3 計算流程及程序準確性驗證

為了更準確計算出徑向滑動軸承的潤滑性能參數,本文計算將滑動軸承從啟動至穩態運動耦合起來計算,計算流程如圖2所示。數值計算流程包括求解啟動階段的滑動軸承潤滑性能和進入穩態工況下的滑動軸承潤滑性能。首先,軸承啟動進入啟動階段,此時采用含有時間項的平均Reynolds方程對壓力分布進行計算,進而得出承載力,根據計算得出的承載力對啟動階段的偏心率進行修正,進而得到啟動階段的偏心率隨時間t變化的軌跡;當偏心率滿足收斂時(如(14)式所示)則進入穩定階段,進而在穩定階段定偏心率下求解滑動軸承潤滑性能。

圖2 計算流程圖

由圖2可知,數值計算循環迭代過程中涉及偏心率、壓力、溫度的收斂性判定。其收斂判斷式為:

|εN+1-εN|≤0.001

(14)

(15)

(16)

圖3為不同傾斜角度下本文模型求解得到最大油膜壓力與文獻[8]中穩態工況下最大油膜壓力的計算結果對比情況。文獻[8]中軸承參數如表2所示。

表2 文獻[8]軸承工況

圖3 本文計算結果與文獻[8]結果對比圖

可以看出,本文潤滑模型的計算結果與文獻[8]中的計算結果具有高度的一致性,驗證了本文計算模型和算法的正確性。

4 軸承潤滑性能分析

4.1 啟動階段至穩態軸心軌跡及潤滑性能

圖4為初始偏心率在0.6和0.8時,表面綜合粗糙度取0.8 μm、無軸頸傾斜的徑向滑動軸承從啟動至進入穩定運行過程中的潤滑性能變化。可以看出, 2種初始偏心率條件下, 隨著時間增加,軸頸瞬時偏心率、承載力、摩擦因數均逐漸增大,最小油膜厚度逐漸減小,相關變化趨勢在23 s左右時達到極值;在23 s后隨著時間進一步增加,偏心率開始緩慢減小、最小膜厚逐漸增大,軸承承載力和摩擦因數則迅速減小,并在44 s左右時,均變為定值,此時意味著徑向滑動軸承進入穩定狀態。

圖4 從啟動至穩定運行過程中滑動軸承性能變化

在時間為23 s左右時偏心率達到最大值0.996,對應油膜厚度達到最小值約為1.77 μm(如圖4b)所示)、對應膜厚比約為2.2,使得軸承表面承載力出現最大值(如圖4c)所示),并顯著增加軸承摩擦力(如圖4d)所示),此時軸承發生大比例粗糙峰接觸,油膜破裂風險最高。另外,初始偏心率不同會使軸承的最大偏心率、最小膜厚、最大承載力、最大摩擦因數產生明顯差異,但是進入穩定狀態后不同初始偏心率對應的軸承性能則趨于一致。因此,選取穩態階段的偏心率作為本文后續工作的研究工況,即在本文中表面粗糙度、軸頸傾斜角度和轉速對滑動軸承性能的影響都是在同一偏心率0.96下進行比較。

4.2 表面綜合粗糙度對滑動軸承啟動階段和穩態工況潤滑性能的影響

啟動階段和穩態工況下徑向滑動軸承的各項潤滑性能參數如圖5所示。由圖5a)和圖5b)對比可以看出,啟動階段表面粗糙度對壓力影響較大,啟動階段軸向截面壓力較穩態工況下的壓力高出約96%,這是因為啟動階段偏心率較大,膜厚較穩態下小,因此固體接觸更加顯著,使得啟動階段壓力大于穩態階段。由圖5c)～5d)可以得出,隨著表面粗糙度由0.6 μm增長至1.2 μm,啟動階段最小膜厚比由3.54減小至1.77(均處于粗糙接觸的破膜風險區),摩擦因數由0.032增加至0.098,微凸體承載比由4.9%增長至24.8%,承載力由2 464 kN增長至2 802 kN;穩態工況下膜厚比由5.06減小至2.53,摩擦因數由0.016增大至0.031,微凸體承載比由2.6%增大至14.6%,承載力由1 869 kN增大至2 242 kN。在表面綜合粗糙度為0.8 μm的情況下,啟動階段最大承載力比穩定階段承載力高出約30.99%,啟動階段最大摩擦因數較穩定階段摩擦因數高出約131.58%。

圖5 無軸頸傾斜時表面綜合粗糙度對軸承潤滑性能的影響

4.3 軸頸傾斜角度對滑動軸承啟動階段和穩態工況潤滑性能的影響

以圖1所示傾斜情況為例,圖6為表面綜合粗糙度為0.8 μm時軸頸傾斜角度對油膜潤滑性能的影響結果,圖6a)～6c)穩定狀態下為有軸頸傾斜且傾斜角度為0.000 2°的膜厚、壓力和溫度分布云圖,可以看出在接近軸承右端面處(即軸向坐標L為0.41 m處)出現膜厚最小值,此處的固體接觸效果更加明顯,因此會出現壓力最大值(如圖6b)所示),同時該處的溫升最大(圖6c))。由圖6d)～6e)可以看出,不論在啟動階段還是穩態工況,軸頸傾斜角度對壓力分布的影響規律是一致的,即隨著傾斜角度的增大,接近軸承右端壓力的最大值增大,且在啟動階段的最大壓力約為穩態工況的2倍。由圖6f)可以看出,無論啟動階段還是穩定階段,軸承承載力和摩擦因數均隨傾斜角度的增加而增大,且啟動階段的最大承載力和摩擦因數比穩定階段平均高出約30%和116%。當傾斜角度從0.000 1°增大至0.000 4°,啟動階段承載力由2 464增大至2 974 kN(增大約20%),摩擦因數由0.048增大至0.082(增大約70.83%);穩態工況下,承載力由1 987 kN增大至2 168 kN(增大約9.1%),摩擦因數由0.021增大至0.04(增大約90.48%),可見軸徑傾斜對滑動軸承性能有很大影響。

圖6 傾斜角度對軸承潤滑性能影響

4.4 轉速對滑動軸承啟動階段和穩態工況潤滑性能的影響

圖7為在表面粗糙度為0.8 μm、軸頸傾斜角度為0.000 2°時不同軸頸轉速對軸承潤滑性能的影響。由圖7a)～7b)可以得出,隨著轉速的增大,啟動階段和穩態工況下的油膜壓力都有一定程度增大,且啟動階段的壓力明顯高于穩定階段,啟動階段油膜軸向截面壓力較穩定階段油膜軸向壓力高出約20%。隨著轉速的增大,油膜動壓效果更加顯著,油膜承載力增大,同時由于膜厚不變,油膜摩擦阻力無明顯變化,因此摩擦因數呈減小趨勢;由圖7c)可以看出,隨著轉速從20 r/min增大至50 r/min,啟動階段承載力由2 184 kN增大至3 068 kN,增大約40.48%,啟動階段摩擦因數由0.046減小至0.031,減小約32.61%;穩態工況下承載力從1 736 kN增大至2 748 kN,增大約58.29%,穩態工況下摩擦因數由0.015 8減小至0.011,減小約30.38%。

5 結 論

基于平均流Reynolds方程,建立滑動軸承的熱流體潤滑數值模型,計算了風電滑動軸承從啟動到穩定過程中的軸心運動軌跡變化,分析了表面綜合粗糙度、軸頸傾斜角度和軸頸轉速對徑向滑動軸承在啟動階段和穩定狀態下潤滑性能的影響。主要結論如下:

1) 在啟動過程中滑動軸承偏心率變化幅度較大,且偏心率的最大值出現在啟動階段。啟動階段膜厚比小于穩態階段的膜厚比,啟動階段的摩擦因數大于穩態階段的摩擦因數,故啟動階段出現粗糙接觸風險高,軸承的摩擦磨損較大。

2) 表面綜合粗糙度對滑動軸承性能有較大影響,當表面綜合粗糙度超過0.8后,膜厚比降至3以下、微凸峰承載比顯著增加。因此在本文的研究范圍內,為了降低不同階段運行過程中的磨損風險,在滿足承載力要求前提下表面綜合粗糙度不宜過大。

3) 在本文研究中,軸頸傾斜可以提升油膜的承載能力,但同時也會造成局部干摩擦增大、油膜局部溫度過高;摩擦因數的增大使得軸承壽命和潤滑性能降低。可以通過適當控制軸頸的傾斜角度來獲得更佳的油膜潤滑性能。

4) 軸頸轉速增大使得軸承的承載力增大,摩擦因數減小;間隙比增大使得軸承的承載力和摩擦因數都減小。因此可以在一定的間隙比下通過適當提升軸頸轉速來獲得更好的潤滑效果。