適用于孤島運行的永磁同步電機自動功率平衡控制策略研究
陸秋瑜 戴耀輝 楊銀國 韓金龍 廖 鵬
適用于孤島運行的永磁同步電機自動功率平衡控制策略研究
陸秋瑜1戴耀輝2楊銀國1韓金龍2廖 鵬1
(1. 廣東電網有限責任公司電力調度控制中心 廣州 510600 2. 西安交通大學電氣工程學院 西安 710049)
該文提出兩種適用于孤島運行的基于永磁同步風機的自動功率平衡控制策略。在控制策略Ⅰ中,風機的網側換流器保持換流器電壓的幅值和頻率為恒定,轉子側換流器通過PI控制器調整功率參考值進而維持直流電壓;在控制策略Ⅱ中,風機網側換流器利用直流母線電壓的動態特性實現電網同步和慣性響應,機側換流器根據直流母線電壓偏差調整有功功率以模擬一次頻率控制。這兩種策略都可以有效地保證風機的獨立運行,無需鎖相環和外部電源。特別地,策略Ⅱ突出了節能特性,將直流電容器中的儲備能量用于系統慣性支持和負荷需求響應,以降低風機飛車的風險。為了提高策略Ⅱ在暫態期間并網點的電壓質量,該文進一步提出維持并網點電壓的改進控制方案。基于PSCAD/EMTDC仿真軟件建立了單臺風機向若干本地負荷供電的典型孤島運行模型,在負荷突然降低或升高的情形下分析和對比了所提兩種策略的有效性。
永磁同步風機 孤島運行模式 自動功率平衡控制 慣量響應 一次調頻 節能特性
0 引言
近年來,新能源在電力系統中的滲透率不斷增大,給交流電網的穩定分析、控制和運行帶來了一系列新的問題和挑戰[1]。傳統的并網變速風機利用轉子側換流器(Rotor Side Converter, RSC)實現最大功率追蹤(Maximum Power Point Tracking, MPPT)。同時,網側換流器(Grid Side Converter, GSC)用于維持直流電壓恒定[2]。然而,此類經典的控制需要鎖相環(Phase Lock Loop, PLL)來獲得公共電壓點(Point of Common Coupling, PCC)的相位,以此維持風機的正常運行。然而,在高比例新能源的弱交流系統中,PLL的動態行為會惡化系統穩定性[3]。此外,基于傳統PLL的風機無法實現自建壓,無法適用于孤島運行方式(Stand-Alone Operation Mode, SAOM)。因此,如何設計新型的并網變速風機的控制策略,以適應高比例新能源滲透的弱交流電網或孤島運行場景,是未來風力發電大規模應用的重要挑戰。
由于優良的控制性能,基于脈沖寬度調制(Pulse Width Modulation, PWM)的電壓源轉換器(Voltage Source Converter, VSC)在工業領域大范圍應用。在功能上,VSC可分為并網模式換流器和離網模式換流器[4-5]。并網換流器控制策略可分為功率相角控制(power-angle control)和矢量電流控制(vector-current control)[6]。功率相角控制通過調整換流器電壓和公共點電壓之間的相位差來控制輸出的有功功率[7];同時,通過調整換流器電壓幅值以控制輸出的無功功率。然而,該策略無法有效地解耦有功功率和無功功率,且無法抑制交流故障引發的換流器過電流現象。矢量電流控制有效地解決了以上兩個問題,并已廣泛應用于風力發電[8]和高壓直流輸電系統[9]中。該控制通過外環(outer loop)即慢環分別控制有功功率和無功功率,內環(inner loop)即快環限制轉子電流的交軸分量[10]。但是,以上兩個控制策略都需要PLL獲取交流系統的同步信息[11],并不適用于離網換流器。
為了提高多換流器系統的穩定性,虛擬同步控制[12-18]成為研究的熱點。該控制策略可分為兩大類:①通過調整換流器外環控制中的有功功率、無功功率參考值,使VSC具備慣量響應[12]、頻率調節[13-15]和區域間阻尼能力[16],這類方案仍然需要PLL獲取電網相位,因此只適用于并網模式;②虛擬同步控制方法被稱作功率同步控制(Power-Synchronization Control, PSC)[17]。該控制策略利用交流系統自身的同步機制,為弱交流系統提供了充足的電壓支撐,實現了無需PLL的同步控制模式。文獻[18]研究了功率同步控制策略的頻率調制能力。文獻[19-20]提出一種利用換流器直流電壓傳遞電網頻率信息的電壓源型控制策略,同時推導了該控制策略的阻尼表達式。文獻[21]提出一種使用虛擬阻抗的虛擬同步機轉子角下垂控制策略。文獻[22]提出一種基于虛擬電流的虛擬同步控制。以上有關功率同步控制的研究大多集中在單換流器范疇,沒有考慮風力發系統中RSC和GSC配合及風力發電機的動態過程。文獻[23]考慮了一種基于雙饋感應電機的功率同步控制策略。
孤島運行模式下變速風力發電機控制策略的設計存在兩個難點:①風機如何自建壓的問題;②如何維持發電機和負荷功率動態平衡的問題。大部分研究[24-25]依賴儲能設備建壓和平衡當地負荷,該方法并不經濟可靠。文獻[26]提出一種在孤島運行模式下,利用風機GSC建立交流電壓,RSC維持直流電壓穩定的控制策略。但該文獻并沒有詳細地論討GSC與RSC的協同配合問題,并且該策略并不適用于多機系統。
結合經典基于PLL的控制策略的不足和孤島運行模式下風機控制策略設計的難點,本文針對PMSG提出了兩種適用于孤島運行模式的自動功率平衡控制策略。控制策略Ⅰ中,風機的GSC側保持換流器電壓幅值和頻率恒定,RSC側通過PI控制器控制有功功率參考值,進而維持直流電壓穩定。這種策略的主要缺點是沒有考慮負荷電壓響應特性,并且可能無法確保SAOM中多風機(Wind Turbine, WT)的功率同步。基于以上缺點,本文進一步提出了控制策略Ⅱ。首先,該策略的GSC根據直流母線電壓的偏差改變換流器電壓頻率以模擬慣性響應,然后RSC根據直流母線電壓變化調節來自WT的有功功率以模擬一次調頻控制。策略Ⅱ利用直流電容器的儲備能量和負荷需求響應平滑系統功率,具有節能特性。兩種策略復雜性更低,控制參數易于實現,只需要測量直流母線電壓即可。為了維持PCC電壓穩定,基于策略Ⅱ提出了一種在GSC控制回路中加入采用PI控制器的電壓控制回路的改進策略,稱之為策略Ⅱ改進策略。之后,研究了直流電壓下垂系數DC變化對直流電壓和調頻效果的影響。以PMSG為例,在負荷突然降低或升高場景下,仿真結果驗證了兩種策略的有效性。最后,研究了風速連續變化情況下兩種策略的有效性。
1 交流系統功率平衡機理
對于任何電網的負荷突變,同步電機通常會依次進行“同步電機電磁功率突變”“同步電機慣量響應”“同步電機一次調頻控制”三個連續階段,以保持發電機和本地負荷之間的平衡。
1.1 同步機電磁功率突變過程
以圖1的單同步機單負荷系統(Single Synchronizing Generator Single Load, SSSL)為例,分析負荷突變引起同步機電磁功率變化的過程。其中同步機為內電動勢恒定的經典模型,其內電動勢用表示;轉子電角度用G表示,假設在負荷突變的初期轉子電角度G不發生突變;發電機暫態阻抗用表示;G和L分別為發電機機端電壓和負荷端口電壓;G為發電機輸出電磁功率;為了簡化,連接發電機和負荷的線路阻抗用l表示。

圖1 單同步機單負荷系統示意圖
圖1中本地負荷L用恒阻抗模型表示為
式中,L和L分別為本地負荷的等效電阻和等效電抗。
根據基爾霍夫電壓定理(Kirchhoffs Voltage Law, KVL),發電機輸出電流G可表示為
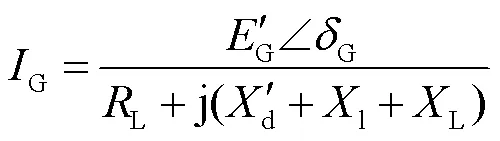
因此,發電機輸出電磁功率G可表示為
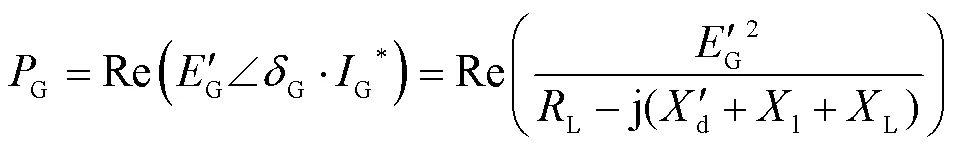
式中,Re(·)表示取復數的實部;“”表示共軛。
為了簡化式(3),將圖1點畫線框中阻抗等效為s,其中s幅值|s|和相角s分別為

合并式(3)和式(4),可得到該SSSL系統中同步發電機輸出的有功功率G為
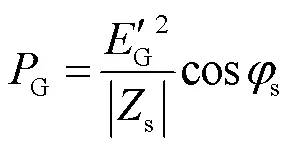
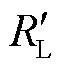

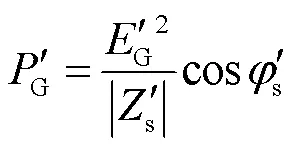
由式(5)和式(7)可知,負荷突變前后,同步機輸出的有功功率變化量為
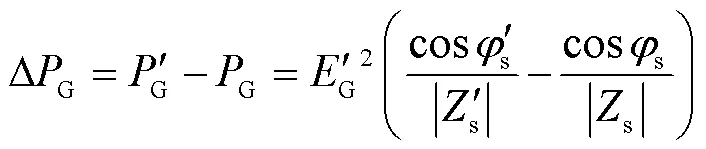
從式(8)可以得到以下同步機功率平衡機理:在SSSL系統中,負荷波動引起發電機慣性響應和一次調頻控制響應。在該暫態過程中,發電機輸出電磁功率的變化只與負荷有關,與發電機轉子電角度無關。
1.2 慣性響應
在該SSSL系統中,負荷突變后,同步機會經歷慣性響應階段,該階段可描述為

式中,B和G分別為該SSSL系統的基準轉速和發電機轉子轉速;G和M分別為同步機轉子慣性時間常數和機械功率。
式(9)表明,負荷突增會引起發電機電磁功率突增,轉子轉速降低和轉子電角度的減小。在SSSL系統中,由于轉子電角度的變化并不影響發電機輸出功率,因此此處不考慮G變化對分析的影響。假設該過程中轉速偏差非常小(G≈1),則式(9)可表示為
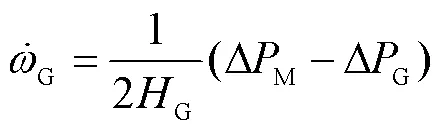
式中,DM為發電機機械功率的變化量。
由于調速系統的響應時間較慢,可認為在同步機慣量響應過程中,一次調頻未啟動。從式(10)中可知,同步機轉子利用自身動能平滑系統頻率波動,這一過程即為同步發電機的慣性響應。
1.3 一次調頻控制
從式(10)中可知,在負荷突變期間,若不調整原動機機械功率輸入,同步機轉子角速度將持續增加或減少。因此,當轉速偏差超過設定閾值時,系統將激活調速系統用于調整原動機的功率,該過程被稱為“一次調頻控制”。調速系統的動態行為可以用下垂系數G和時間常數g描述,有
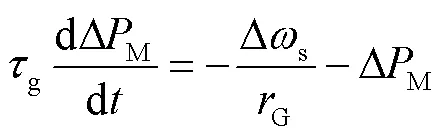
由式(11)可得,系統經歷一次調頻控制之后,同步機轉速偏差為
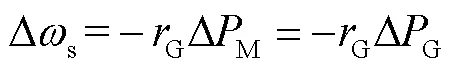
綜上分析,同步機利用轉速來傳遞發電機和負荷之間的功率不平衡信息。同時,調速系統基于經典的功率-頻率下垂特性響應系統頻率的變化,以此保證發電機和負荷之間功率的動態平衡。
2 基于PMSG的自動功率平衡控制策略Ⅰ
為了模擬同步機的優良特性,類比第1節交流系統的同步機理,本文提出了兩種全新的自動功率平衡控制策略。
2.1 網側換流器控制策略
圖2為PMSG的網側換流器結構,其中換流器通過換流器等效阻抗C與本地負荷連接,構成了一個單換流器單負荷系統。

圖2 單換流器結構
以圖2單換流器單負荷系統為例,同樣分析負荷突變造成換流器功率變化的過程和機理。其中,PMSG并網點的電容補償器等效容抗表示為C;DC為直流電壓;換流器交流電壓用C∠C表示,其中C為換流器電壓幅值,C為換流器電壓相角;PCC和L分別為換流器PCC電壓和負荷端口電壓;C為換流器輸出功率;為了簡化,連接換流器和負荷的線路阻抗用l表示。
根據VSC的基本工作原理,通過控制IGBT的開關動作,換流器交流電壓的幅值和頻率可被控制在任意可行值。在控制策略Ⅰ中,GSC側保持換流器交流電壓幅值和頻率恒定,有效地將換流器交流電壓C和同步機暫態電勢進行類比。VSC直流電壓DC和換流器交流電壓C(線電壓)之間的關系為
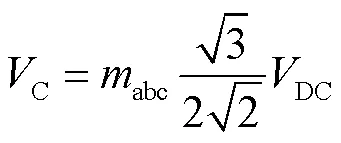
式中,abc為換流器A、B、C三相交流電壓的調制比。本文不考慮三相不對稱情況,可認為a=b=c=。
因此,調制比可表示為

式中,C和DC分別為換流器交流電壓和直流電壓的參考指令值。
在控制策略Ⅰ中,調制比、換流器電壓的頻率和相角C被設定成固定值,即
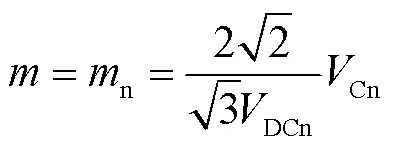

式中,C0為換流器電壓相角的初始值;n為換流器調制比的標稱值;DCn和Cn分別為直流母線電壓和換流器電壓的標稱值。
按照式(15)和式(16),采用正弦脈寬調制法,即可產生固定頻率和幅值的電壓波形。
仿照1.1節的分析,圖2中的單換流器單負荷系統在發生電磁功率變化前后,網絡的等效阻抗變化可分別表示為


因此,同樣可以寫出PMSG網側換流器輸出功率變化量DC,I的表達式為

式(19)說明在換流器中同樣存在類似同步機的功率平衡機理:在單換流器單負荷系統中,換流器在暫態期間輸出功率的變化只與負荷有關,與換流器交流電壓的相角無關。因此,C0可在0~2p中任意取值。為了簡化,此處C0可設置為0。
2.2 轉子側換流器控制策略
在傳統的PMSG控制策略中,RSC側控制以實現最大功率追蹤(MPPT)算法和調整PMSG和RSC之間的無功交換為目標。然而,MPPT算法無法應用于孤島運行模式或離網運行模式。在該運行模式下,RSC的控制目標應為實時保持風力機和當地負荷之間的功率平衡。圖2中,PMSG的直流電容器的動態行為可描述為
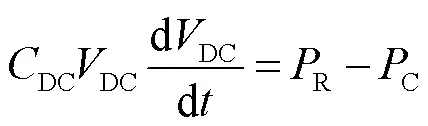
在孤島運行模式下,為了滿足風力發電機和當地負荷之間功率的實時平衡,R由當地負荷或C決定。由式(20)可知,在兩端VSC中,發電機和負荷之間任意有功功率的不平衡會引起直流電壓的變化。對比式(20)和式(10),換流器的直流電容動態響應和同步機慣量響應在形式上具有高度的一致性。因此,在暫態過程中直流母線電壓可以作為反饋信號跟蹤本地負荷波動,以及控制RSC的有功功率,維持功率平衡。以上功率平衡機制和同步機利用系統頻率信號進行功率調整的機制是完全類似的。綜上所述,在風力發電機孤島運行模式下,RSC的功率R可設置為
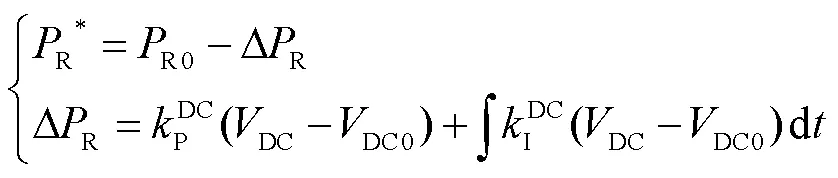
式中,DR為直流電壓控制環PI控制器的輸出量;PDC和IDC分別為直流電壓控制環PI控制器的參數;R0為RSC控制回路中,功率參考值的初始值。
鑒于換流器的快速調制能力,本文分析中認為RSC實際的功率輸出能夠實時跟蹤功率參考值,即R=R*。在該策略下,任意負荷波動都會引起直流電壓的波動,進而引起RSC有功功率參考值R的調整,以確保兩端換流器之間的功率平衡。此外,由于換流器功率平衡是通過控制直流電壓實現的,R0可設置為任意可行值。
在負荷波動期間,為了避免DR的大范圍波動,R0可設置為GSC輸出功率C在某段時間內的平均值,有
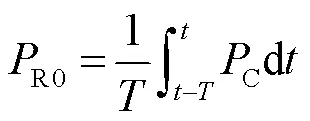
在該策略下,風力機捕捉的風能W和RSC有功功率R之間的不平衡會引發永磁電機轉子加速或減速,該動態過程可描述為

式中,r和WT分別為轉子轉速和慣性時間常數。
在本節分析中,假設風能資源是充足的,因此,在系統暫態期間,通過超速控制或槳距角控制,風輪機捕捉的風能最終會和RSC輸出的有功功率達到平衡。綜上所述,基于PMSG的自動功率平衡控制策略Ⅰ的整體控制框圖如圖3所示。

圖3 控制策略Ⅰ整體控制框圖
3 基于PMSG的自動功率平衡控制策略Ⅱ
在策略Ⅰ中,PMSG的GSC負責產生恒定的交流電壓,RSC負責平衡發電機和負荷之間的功率平衡。該策略的功率平衡機理和傳統的同步機利用系統頻率偏差進行功率調整的機制是完全類似的。但是,該策略存在兩個突出的缺點:①策略Ⅰ的控制目標為產生恒定幅值和頻率的換流器交流電壓,因此在負荷波動期間,它無法利用負荷潛在的電壓或頻率特性來幫助系統功率恢復平衡,也不適用于多風機系統(這一點將在3.4節說明);②策略Ⅰ僅僅是利用直流電容的動態方程,將直流母線電壓作為反饋信號跟蹤本地負荷波動,以及控制RSC的有功功率,維持功率平衡,而沒有模擬同步機的慣量響應和一次調頻控制過程,無法為系統提供有效的慣量支撐。因此,本節提出了基于PMSG的自動功率
平衡控制策略Ⅱ。該策略充分模擬同步機慣量響應和一次調頻過程,進而為系統提供有效的慣量支撐,且能有效應用于離網模式和并網模式。
3.1 網側換流器控制策略
3.1.1 慣量模擬
與第2節中提出的控制策略Ⅰ類似,策略Ⅱ中PMSG的GSC需要具備網絡自建壓的能力。與控制策略Ⅰ不同的是,控制策略Ⅱ中換流器交流電壓頻率不被控制為恒定值。第2節分析表明,在負荷變化期間,直流電壓可傳遞系統頻率波動信息。為了讓GSC模擬同步機慣量響應過程,策略Ⅱ將系統頻率和直流電壓人為耦合起來。穩態情況下,假設換流器的交流電壓頻率為0,幅值為C,相角為0,直流電壓穩態值為DC0。在圖2中,當負荷發生突變時,由式(19)可知,GSC輸出功率也會突變。在此期間,直流電壓的動態過程為

由式(24)可知,兩端換流器之間任意的功率不平衡信息會反映到直流電壓波動上。對比式(10)和式(24)可知,直流母線電壓的動態響應過程和同步機的慣量響應過程十分類似。因此,直流電壓通過式(25)準則和系統頻率偏差進行人為耦合。

式中,DC為電壓下垂控制的比例系數。
在系統動態期間,假設直流母線電壓在標稱值DC0附近小幅度波動,結合式(24)和式(25),GSC的小信號模型為
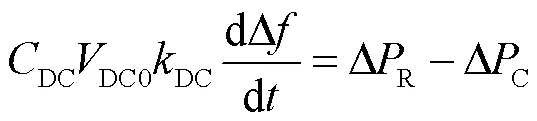
由式(26)可得,RSC和GSC之間任意的功率不平衡會導致系統頻率的改變,該機制和傳統同步機的慣量響應過程類似。不同的是,傳統的同步機利用轉子質量塊動能平衡系統功率的波動,而換流器利用電容儲存的能量平滑系統功率的波動。因此,基于式(26),可以得出該控制策略的等效慣性時間常數C為

式(27)說明,在允許范圍內,直流電容越大、直流電壓環節下垂系數越大,在負荷波動期間,策略Ⅱ能為系統提供的慣量支撐就越多。綜上所述,控制策略Ⅱ中,GSC的控制法則為


3.1.2 網側換流器改進策略
根據3.1.1節的分析,直流電容儲存的能量在系統暫態期間可被利用于系統慣量支撐。該過程會引發直流電容電壓和換流器交流電壓的波動,雖然其利用了負荷的電壓響應特性用于快速的功率平衡,但是一定程度上損失了電壓穩定性。結合式(13)、式(14)、式(25)及轉子側控制策略(見式(32)~式(34)),在策略Ⅱ中,負荷波動期間,換流器電壓偏差為

式中,f為模擬一次調頻過程的下垂系數。
式(30)表明,負荷波動期間,換流器交流電壓的波動和風機的頻率下垂系數、直流電壓參考值、負荷功率波動等因素有關。因此,當系統經歷大的負荷波動或者控制參數設計不合理時,換流器電壓偏差會過大,嚴重影響負荷的電壓質量,這在實際應用中是無法接受的。為了維持PCC電壓的穩定,在策略Ⅱ基礎上加入PCC電壓控制回路,并將此策略稱為策略Ⅱ改進策略(注:本文中所涉及的策略Ⅱ均指無PCC電壓控制回路的控制策略,即使用3.1.1節所提網側控制策略,在策略Ⅱ基礎上加入PCC電壓控制回路的策略稱之為策略Ⅱ改進策略)。在系統暫態期間,GSC利用PI控制器,通過改變調制比來維持PCC電壓恒定。該控制思路和傳統同步機的勵磁調節系統非常類似。因此,調制比的控制法則可描述為

3.2 轉子側換流器控制策略


R0的設置原則和控制策略I類似。
結合式(26)和式(32),控制策略Ⅱ中,PMSG的頻率響應模型為

穩態時系統頻率偏差為
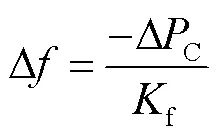
在該控制策略下,PMSG的兩端換流器之間的功率最終會達到平衡。由式(13)可知

則

暫態期間通過調整式(36)所表示的換流器電壓實現負荷需求響應,以系統負荷阻抗突增為例,在策略Ⅱ中,式(24)和式(34)表明,進入新的平衡狀態后,直流電容電壓和系統頻率都會下降。同時,基于式(36),換流器電壓會在可接受范圍內自發地下降。PMSG網側換流器輸出功率變化量DC,II為
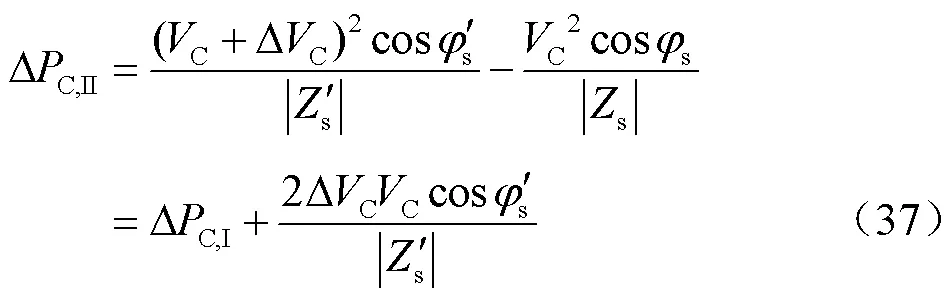
式中,ΔC<0。
因此,在負荷阻抗變化相同的情況下,策略Ⅱ負荷有功功率的增加相比于策略Ⅰ會更少。
以上分析說明,策略Ⅱ充分利用了負荷的電壓響應特性和直流電容儲備能量以幫助系統快速恢復功率平衡,降低了風機在負荷變化時飛車的風險。并且在系統動態過程中,每個換流器都會響應負荷變化,同時共同協調實現快速的功率平衡,對孤島系統來說具有節能效益,也適用于多風機系統。基于PMSG的自動功率平衡控制策略Ⅱ(含改進策略)的整體控制框圖如圖4所示。
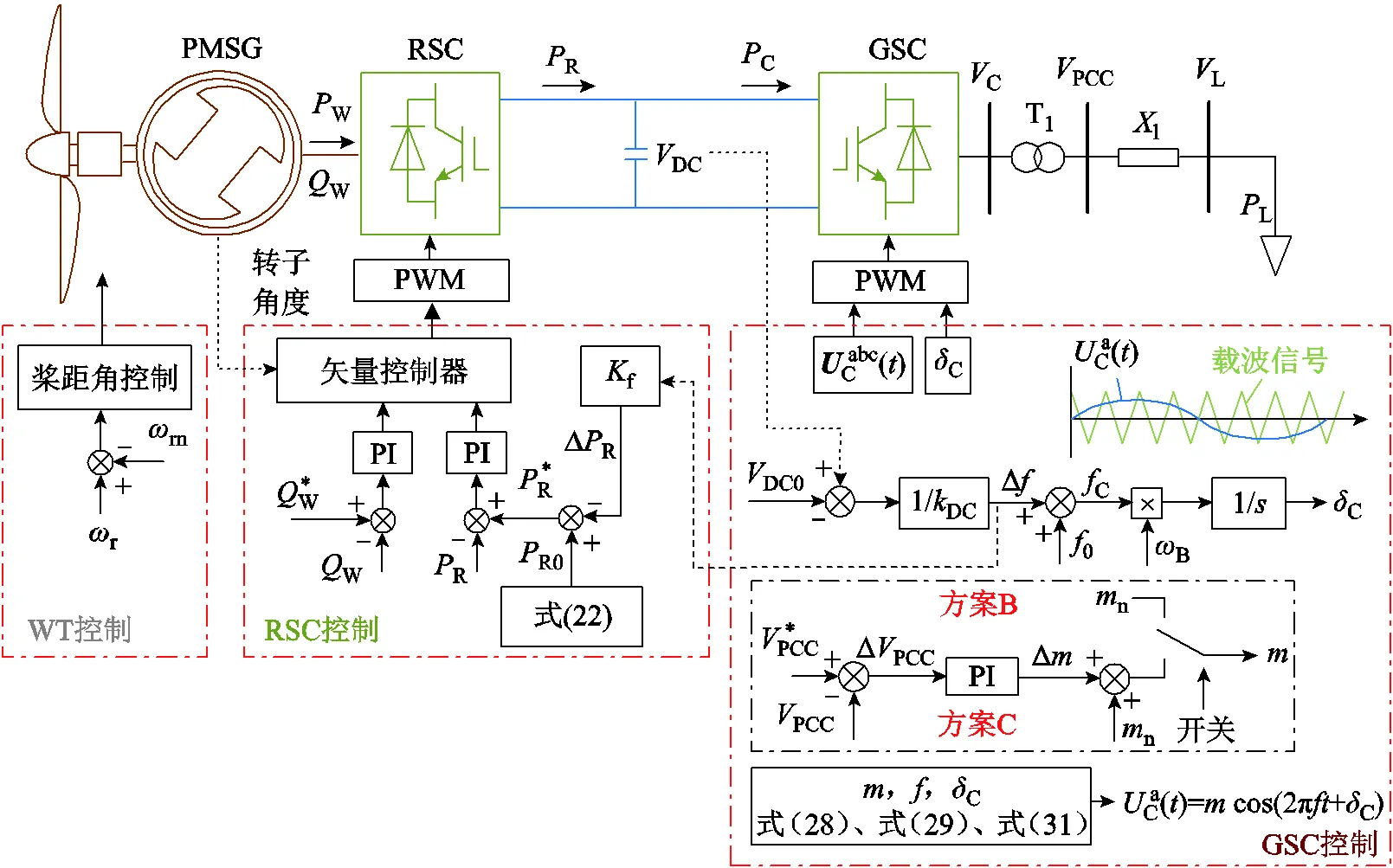
圖4 控制策略Ⅱ整體控制框圖
3.3 重要參數的整定過程
在策略Ⅱ中,有兩個核心參數需要設計:網側換流器直流電壓環節的下垂系數DC和轉子側換流器一次調頻下垂系數f。合理設計這兩個參數,有助于提高孤島運行方式下PMSG的穩定性,同時為系統提供更多的慣量支撐。下面詳細介紹這兩個參數的設計原則。
在系統動態過程中,直流電壓的波動不能超過10%。為了充分利用直流電容的能量為系統提供慣量支撐,直流電容波動能量至少預留一半的裕度以防系統嚴重的頻率偏差。假設系統在經歷暫態過程中,直流電壓可承受偏差的最大值為ΔDCmax,系統頻率可接受偏差的最大值為Δmax。在系統頻率偏差較大時,直流電容波動的能量至少要釋放一半去為系統提供支撐,因此可得出

整理可得

將式(39)進行縮放

實際運行中,直流電容電壓需要控制在一個安全范圍內以防電容擊穿。因此在系統經歷最大的頻率波動Δmax時,直流電容電壓波動也不能超過ΔDCmax。容易得出,直流電壓下垂系數DC需控制在式(41)范圍內。

轉子側換流器一次調頻下垂系數f的選擇需要同時考慮系統經歷的最大負荷波動(將網側換流器經歷的最大有功功率波動記為ΔCmax),與頻率的穩態偏差的最大值Δsmax。因此一次調頻下垂系數f可用式(42)確定。
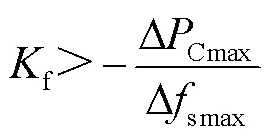
另外,直流電容的大小為
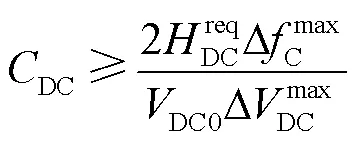
3.4 多機系統中兩種策略適應性
在多機系統中,由于換流器電壓幅值和頻率被控制為恒定值,策略Ⅰ沒有考慮功率共享特性。由式(21)可知,在策略Ⅰ下,功率的分配僅與負荷波動有關。由于實際運行中難以確定負荷阻抗的變化量,每臺PMSG的RSC側有功功率參考值難以確定,功率的波動容易導致機組停機。所以策略Ⅰ不適用于多機系統。而由式(25)和式(32)可知,策略Ⅱ通過GSC頻率的變化響應負荷變化,每臺機組均按照其RSC的一次調頻下垂系數的大小分配功率。在系統動態過程中,雖然系統負荷的變化難以確定,但是在控制策略Ⅱ下,每個RSC有功出力的份額是確定的,且與該換流器一次調頻下垂系數成正比。在該方案下,通過合理設計控制參數可以很好地實現多機系統的功率協同分配。
本文將不涉及在所提策略下有關換流器動態交互的更多討論,并將在未來做進一步研究。
4 仿真分析
4.1 仿真平臺及算例
為了驗證所提兩種控制策略的有效性,在電磁暫態仿真軟件PSCAD/EMTDC中搭建如圖5所示孤島測試系統。

圖5 仿真測試系統簡化框圖
該系統中,PMSG額定功率為2 MW。兩個本地負荷L1和L2用恒阻抗模型L+jL表示。其中L1為10+j1.63W,L2為17+j0.93W。系統中,PMSG的PCC電壓被控制在3 kV,換流器電感為0.005 H,變壓器阻抗為0.001(pu),PMSG并網點固定電容器為108.3mF,線路阻抗l為0.02+j0.0157W。其余參數詳見附錄。為了方便對比不同控制策略,設計了三種控制方案進行對比:
方案A:采用策略Ⅰ,風機的GSC側保持換流器電壓幅值和頻率恒定,RSC側維持直流電壓穩定。
方案B:采用策略Ⅱ,風機的GSC側利用直流母線電壓的動態特性實現電網同步和慣性響應,RSC側換流器根據直流母線電壓偏差調整有功功率以模擬一次頻率控制。
方案C:采用策略Ⅱ改進策略,調制比不為恒定值。在系統暫態期間,GSC利用PI控制器,通過改變調制比來維持PCC電壓恒定。
4.2 負荷突增場景
該場景在穩態運行情況下,系統由一臺PMSG向本地負荷L1供電。方案A中直流電壓控制環的PI參數分別為1和5;方案B和方案C中直流電壓下垂系數和一次調頻系數分別為1和2。在=2 s時,投入本地負荷L2,系統的動態響應結果如圖6所示。從仿真結果分析,三種方案都能在沒有PLL和外部電源的孤島運行模式下有效運行,同時保證發電機和負荷之間的功率平衡。
在負荷突增之后,圖6a中方案A的PCC電壓有效值從3.0 kV跌落到2.93 kV(穩態值),以此適應負荷功率的突增。由于圖6e中直流電壓的跌落,圖6a和圖6b中方案B的換流器電壓和PCC電壓有明顯跌落。因為策略Ⅱ的GSC側能夠為系統提供慣量支撐,圖6d中方案B和C的PMSG輸出有功功率變化速度比方案A更加緩慢。圖6e中方案B的直流電壓從6 kV跌落至5.8 kV,犧牲的電容能量被用于系統慣量支撐。從圖6a中可知,對比三種方案,方案B的PCC電壓從3 kV跌落至2.85 kV,是三種方案里跌落率最高的,這在正常運行過程中是無法接受的。為了維持PCC電壓,方案C在暫態期間通過自發提高調制比,升高圖6b中的換流器電壓,將PCC電壓穩定在3 kV,能夠有效穩定負荷電壓。對比圖6c和圖6d可知,在經歷相同負荷阻抗波動下,由于三種方案PCC電壓偏差不同,它們的負荷功率變化也不同。方案B充分利用了負荷的電壓特性幫助系統快速恢復功率平衡。

圖6 負荷突增場景系統動態響應
圖6g和圖6h表明,由于RSC的快速功率調制能力,風力機的槳距角和PMSG的轉速在系統動態期間會快速響應負荷變化,以維持捕獲的風能與PMSG輸出功率之間的動態平衡。在方案B中,由于負荷有功功率偏差是最小的,風力機仍然處于槳距角控制模式,同時,PMSG的轉速保持在最大轉速1.25(pu)。經計算可得,策略Ⅰ在負荷突增后8 s時間內輸出電能10.725 MJ,采用策略Ⅱ后會節省電能(陰影面積)0.536 MJ,節省了約5%的電能,減輕了系統負擔。因此,方案B利用直流電容器中的儲備能量和負荷電壓特性穩定系統,這對于孤島運行的系統而言更加節能。方案A和方案C的GSC側所需有功功率更大,因此這兩個方案的PMSG均處于超速運行模式,風力機槳距角均降為0。
4.3 負荷突降場景
該場景在穩態運行情況下,系統由一臺PMSG向兩個本地負荷L1和L2供電。系統控制參數與4.2節相同。在=2 s時,切除本地負荷L2,系統的動態響應結果如圖7所示。
在方案A中,從圖7f和圖7b可知,由于GSC控制交流電壓幅值和頻率恒定,發電機和負荷之間的任意功率波動都反映在直流電壓的波動中。為了維持直流電壓恒定,RSC利用PI控制器調整功率參考值,進而維持換流器兩端功率平衡。從圖7d中可以看出,在負荷突降之后,RSC輸出有功功率迅速減小。由于換流器電感的存在,負荷突降后,方案A中PCC電壓有效值上升。因此,相比于方案C的恒定PCC電壓控制模式,方案A的負荷有功功率會更大。
為了維持系統頻率,相比于方案B,在圖7g和圖7h中方案A需要更大的轉速偏差和風能犧牲。為了維持發電機和負荷之間的功率平衡,圖7g中PMSG轉速迅速升高,圖7h中風力機的槳距角控制會隨機啟動以此減少風輪捕獲的風能,從而防止風機飛車。在方案B和方案C中,從圖7e和圖7f中可以得到,為了使PMSG具備慣量響應和一次調頻能力,負荷突降之后,系統頻率和直流電壓自發地升高。相比于方案A,該過程使得RSC輸出的有功功率波動更加平滑。同時,從圖7a和圖7b中可知,由于方案B中直流電壓的升高,PCC電壓和換流器電壓也顯著升高。相比于方案A和C,這一特性使得負荷的功率降低的最少。方案B再一次利用了負荷的電壓調節特性幫助系統快速恢復功率平衡。從圖7a和圖7b中可知,方案C有效地維持了PCC電壓恒定,因此也能維持負荷電壓穩定。相比于方案A和方案B,負荷突變后,方案C中負荷有功功率最低,且風力機槳距角最大。
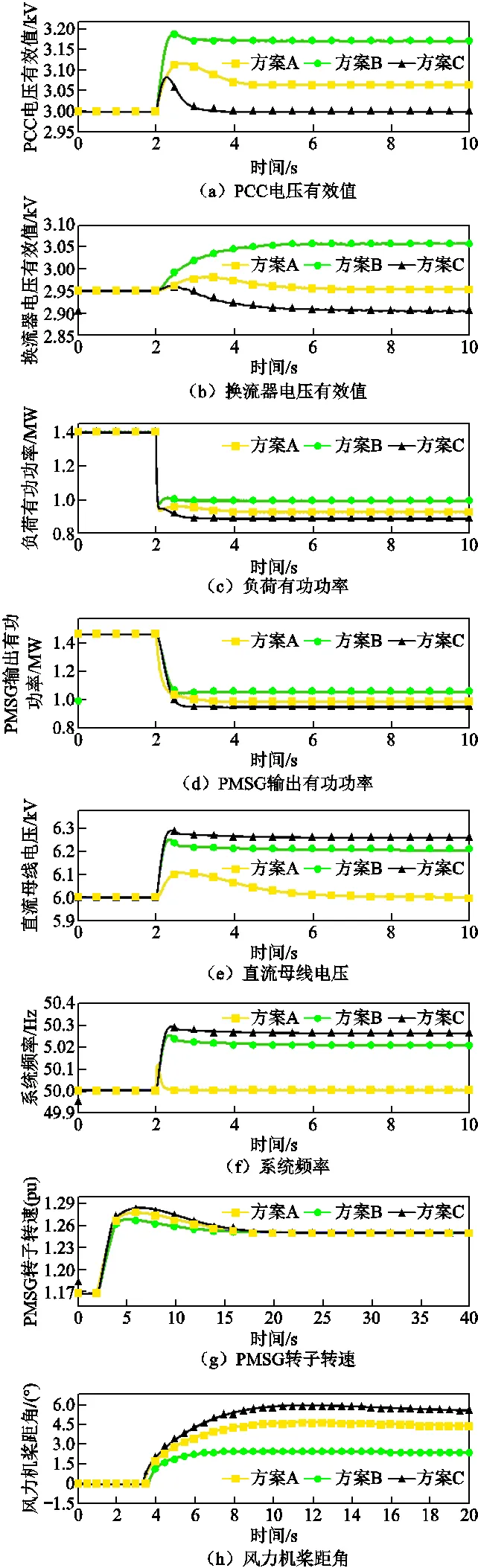
圖7 負荷突降場景系統動態響應
4.4 kDC變化對直流電壓和調頻效果的影響
該場景在穩態運行情況下,以負荷突增情況為例,系統由一臺PMSG向本地負荷L1供電。選取方案B,一次調頻系數設置為2,直流電壓下垂系數DC的倒數分別設置為0.6、0.8、1、1.1。在=2 s時,投入本地負荷L2。系統的動態響應結果如圖8所示。
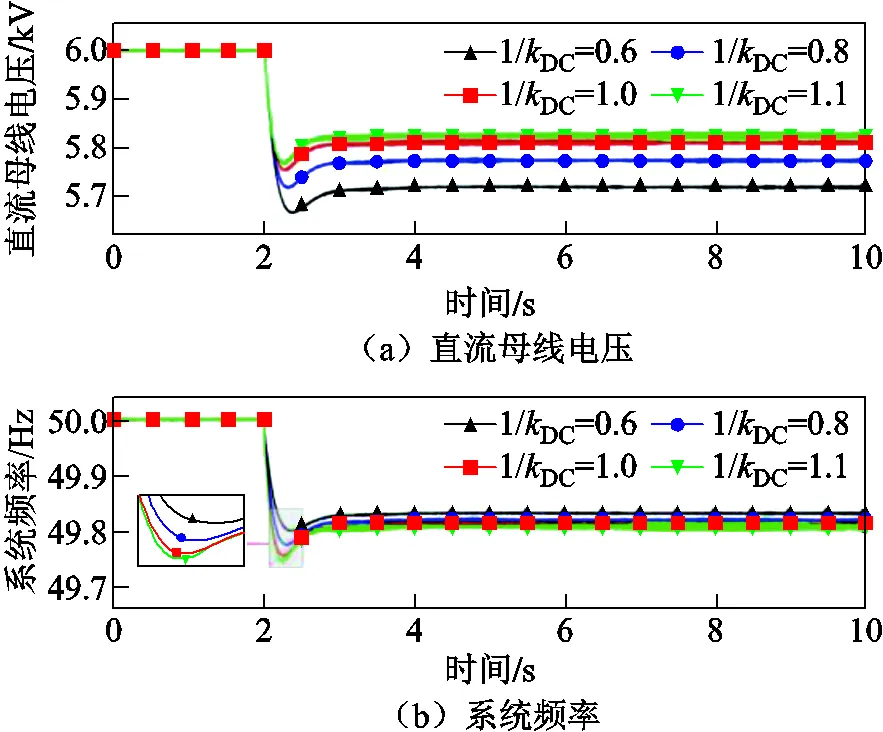
圖8 不同kDC下的系統動態響應
在孤島運行系統中,系統動態過程中直流電壓的波動不能超過10%,在系統頻率偏差較大時,直流電容波動的能量至少要釋放一半去為系統提供支撐。由圖8可知,實驗所選DC均能滿足此要求。在負荷突增后的暫態過程中,圖8a中的直流母線電壓波動隨DC的增大而增大,在1/DC取0.6的時候,直流母線電壓最低跌至5.7 kV以下;圖8b中的系統頻率波動隨DC的增大而減小,在1/DC取1.1的時候,系統的頻率最低跌至49.7 Hz。
這表明在負荷突增之后,DC越大,直流母線電壓波動就越大,從直流電容中釋放出用于系統慣性支撐的能量就越多,因此,系統頻率的波動就越小。
4.5 風速連續變化場景
該場景設置在5 s后風速連續變化情況下,其中風速平均值為11 m/s,標準偏差為1.5 m/s。系統受擾前單獨為本地負荷L1供電。方案A中直流電壓控制環的PI參數分別為1和5;方案B和方案C中直流電壓下垂系數和一次調頻系數分別為1和2。系統的動態響應結果如圖9所示。
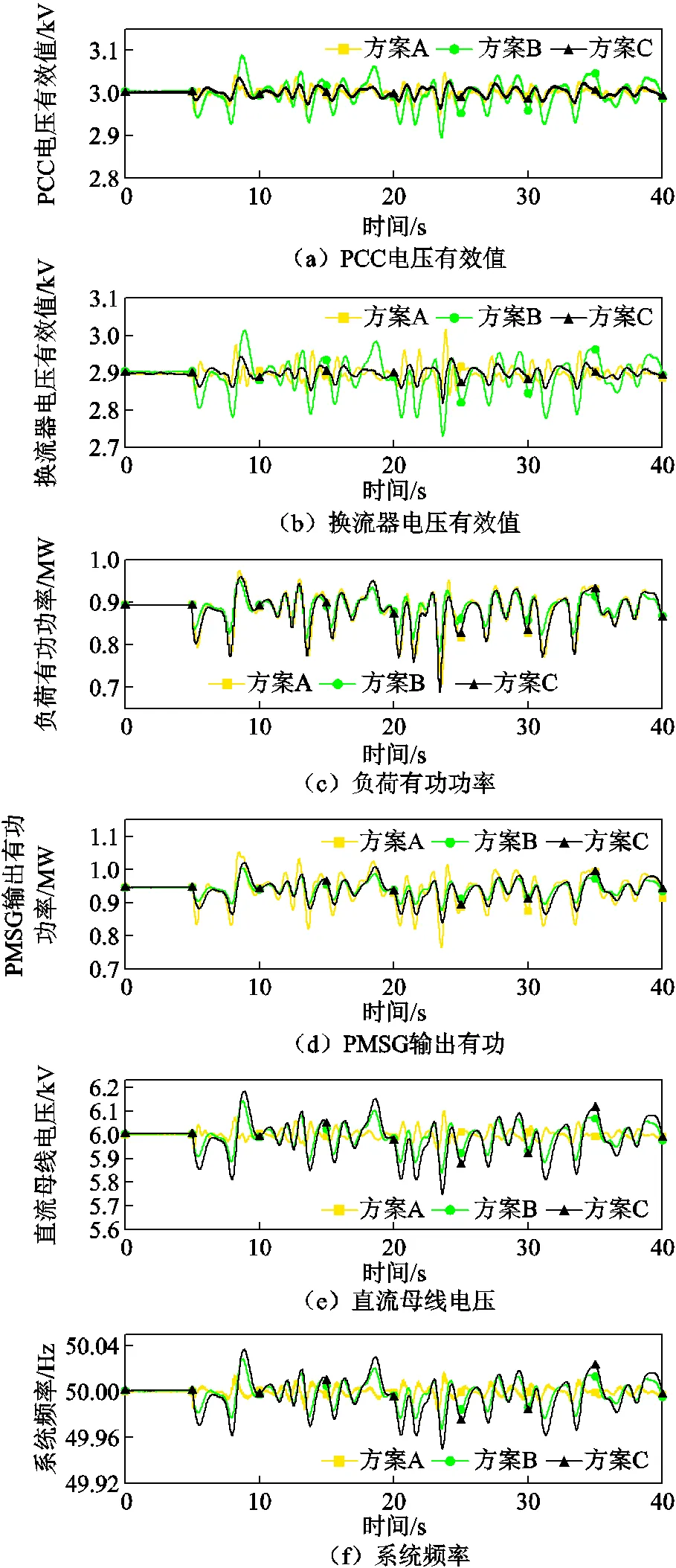
三種方案都能在風速連續變化情況下,保持在孤島系統下的穩定運行,無需PLL和外部電源。并且所有系統變量的波動都在可接受范圍內。如圖9a、圖9e和圖9f所示,與方案B和方案C相比,方案A的PCC電壓、直流母線電壓和系統頻率均保持良好。然而,如圖9d、圖9g和圖9h所示,與其他兩種方案相比,方案A需要永磁同步電機提供更多的能量以維持功率平衡和PCC電壓穩定,因此方案A的風機轉子轉速和槳距角產生最大偏差。方案A沒有利用負荷需求響應,在系統功率波動期間,風機需要更大的轉速偏差和風能犧牲以維持系統頻率,這將提高風機運行成本,并可能導致某些情況下風機飛車。
另一方面,方案B和方案C通過利用圖9e中的直流母線電壓波動使得風機具有慣性響應和一次調頻能力。如圖9e和圖9f所示,方案B和方案C通過控制直流母線電壓偏差以響應系統功率波動和頻率偏差。在系統動態過程中,直流電容中儲存的能量將被利用以維持系統功率平衡,并減輕風機的負擔。此外,如圖9a所示,方案B充分利用負荷需求響應,在允許范圍內自發調整PCC電壓。因此,如圖9d、圖9g和圖9h所示,方案B需要永磁同步電機提供用以維持穩定運行的能量最少,因此在風速連續變化期間,方案B風機的轉速和槳距角的波動最小。由圖9可知,與方案B相比,盡管方案C能有效地維持住PCC電壓,但卻造成PMSG輸出功率、直流母線電壓、轉子轉速和槳距角的更大偏差。
因此可以得出結論:在系統動態過程中,方案A能夠很好地維持系統頻率,但會提高系統的運行成本;方案B和方案C能夠利用直流電容器儲備能量維持功率平衡,減輕風機負擔,特別地,方案B利用負荷需求響應,降低了風機飛車的可能性;方案C能夠有效地維持PCC電壓,但也會導致更大的直流母線電壓偏差以及風機轉速和槳距角偏差。
綜上所述,三種控制方案都適用于無PLL和外部電源的PMSG孤島運行模式。策略Ⅰ將交流電壓和頻率控制為固定值。策略Ⅱ在暫態過程中,通過自發地改變直流電壓進而模擬同步機慣量響應過程,為系統提供有效的慣量支撐。策略Ⅱ同時適用風機的并網模式和離網模式,具有節能效果且能給弱交流系統提供有效的電壓支撐。對比方案A,方案B利用了負荷的電壓響應特性幫助系統恢復功率平衡,在很大程度上降低了風力機飛車的可能性。基于方案B的PCC電壓波動過大可能對負荷電壓質量造成影響的問題,進一步提出了方案C,能夠有效地穩定PCC電壓,維持負荷電壓穩定。之后,研究了DC變化對直流電壓和調頻效果的影響,負荷增加時,DC越大,直流母線電壓波動就越大,從直流電容中釋放出用于系統慣性支撐的能量就越多,系統頻率的波動就越小。最后,研究了在風速連續變化情況下三種方案的運行特性。三種方案都能在風速連續變化情況下,保持在孤島系統下的穩定運行,無需PLL和外部電源。以上三種控制方案對未來風力發電機應用領域有十分顯著的指導意義。
5 結論
1)基于孤島離網運行模式下的PMSG,本文提出了兩種全新的自動功率平衡控制策略。兩種控制策略都無需PLL和外部電源。
2)相比于策略Ⅰ,策略Ⅱ利用負荷的電壓特性和直流電容器儲備能量平滑系統功率,具有節能效應。策略Ⅱ改進策略能夠在系統動態期間維持PCC電壓穩定性,保證負載電壓質量,但相應地會失去節能特性。
3)直流電壓下垂系數DC的變化對直流電壓和調頻效果有一定的影響。負荷增加時,DC越大,直流母線電壓波動就越大,從直流電容中釋放出用于系統慣性支撐的能量就越多,系統頻率的波動就越小。
4)通過仿真驗證了三種方案在風機孤島運行模式下的有效性。其中,策略Ⅱ以其慣量響應、一次調頻控制、利用負荷的電壓調節特性和直流電容器儲備能量節能等優良特性,對未來風力發電的大規模運用有重要意義。
附 錄

附表1 風機參數

附表2 PMSG參數
[1] 馬進, 趙大偉, 錢敏慧, 等. 大規模新能源接入弱同步支撐直流送端電網的運行控制技術綜述[J]. 電網技術, 2017, 41(10): 3112-3120.
Ma Jin, Zhao Dawei, Qian Minhui, et al. Reviews of control technologies of large-scale renewable energy connected to weakly-synchronized sending-end DC power grid[J]. Power System Technology, 2017, 41(10): 3112-3120.
[2] Chang-Chien L R, Lin Weiting, Yin Y C. Enhancing frequency response control by DFIGs in the high wind penetrated power systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 710-718.
[3] 吳恒, 阮新波, 楊東升. 弱電網條件下鎖相環對LCL型并網逆變器穩定性的影響研究及鎖相環參數設計[J]. 中國電機工程學報, 2014, 34(30): 5259-5268.
Wu Heng, Ruan Xinbo, Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.
[4] Li Yujun, Xu Zhao, ?stergaard J, et al. Coordinated control strategies for offshore wind farm integration via VSC-HVDC for system frequency support[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 843-856.
[5] 王盼寶, 王衛, 孟尼娜, 等. 直流微電網離網與并網運行統一控制策略[J]. 中國電機工程學報, 2015, 35(17): 4388-4396.
Wang Panbao, Wang Wei, Meng Nina, et al. Unified control strategy of islanding and grid-connected operations for DC microgrid[J]. Proceedings of the CSEE, 2015, 35(17): 4388-4396.
[6] Svensson J. Grid-connected voltage source converter[D].Gothenburg: Chalmers University Technol, 1998.
[7] Fischer P. Modelling and control of a line-commutated HVDC transmission system interacting with a VSC STATCOM[D]. Stockholm: Royal Institute of Technology, 2007.
[8] Li Shuhui, Haskew T A, Swatloski R P, et al. Optimal and direct-current vector control of direct-driven PMSG wind turbines[J]. IEEE Transactions on Power Electronics, 2012, 27(5): 2325-2337.
[9] Zhang Lidong, Harnefors L, Nee H P. Modeling and control of VSC-HVDC links connected to island systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 783-793.
[10] Egea-Alvarez A, Fekriasl S, Hassan F, et al. Advanced vector control for voltage source converters connected to weak grids[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3072-3081.
[11] Wen Bo, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 675-687.
[12] Kayikci M, Milanovic J V. Dynamic contribution of DFIG-based wind plants to system frequency disturbances[J]. IEEE Transactions on Power Systems, 2009, 24(2): 859-867.
[13] Li Yujun, Xu Zhao, Wong K P. Advanced control strategies of PMSG-based wind turbines for system inertia support[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3027-3037.
[14] 顏湘武, 賈焦心, 王德勝, 等. 基于/“導納”的并聯虛擬同步機功頻響應建模與分析[J]. 電工技術學報, 2020, 35(15): 3191-3202.
Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al. Modeling and analysis of active power-frequency response of parallel VSGs using a/“admittance”[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3191-3202.
[15] 于彥雪, 關萬琳, 陳曉光, 等. 基于序阻抗的虛擬同步機同步頻率諧振現象[J]. 電工技術學報, 2022, 37(10): 2584-2595.
Yu Yanxue, Guan Wanlin, Chen Xiaoguang, et al. Synchronous frequency resonance in virtual sychronous generator based on sequence-impedance[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2584-2595.
[16] Liao Kai, He Zhengyou, Xu Yan, et al. A sliding mode based damping control of DFIG for interarea power oscillations[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 258-267.
[17] Zhang Lidong, Harnefors L, Nee H P. Power-synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.
[18] Guan Minyuan, Pan Wulue, Zhang Jing, et al. Synchronous generator emulation control strategy for voltage source converter (VSC) stations[J]. IEEE Transactions on Power Systems, 2015, 30(6): 3093-3101.
[19] 楊仁炘, 張琛, 蔡旭. 具有頻率實時鏡像和自主電網同步能力的風場–柔直系統控制方法[J]. 中國電機工程學報, 2017, 37(2): 496-506.
Yang Renxin, Zhang Chen, Cai Xu. Control of VSC-HVDC with real-time frequency mirroring and self-synchronizing capability for wind farm integration[J]. Proceedings of the CSEE, 2017, 37(2): 496-506.
[20] 楊仁炘, 施剛, 蔡旭. 海上全直流型風電場的電壓源型控制[J]. 電工技術學報, 2018, 33(2): 546-557.
Yang Renxin, Shi Gang, Cai Xu. Voltage source control of offshore all-DC wind farm[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 546-557.
[21] 伍興煌, 魏強. 使用虛擬阻抗的虛擬同步機轉子角下垂控制[J]. 電氣技術, 2020, 21(3): 31-36, 58.
Wu Xinghuang, Wei Qiang. Virtual synchronous machine rotor angle droop control using virtual reactance[J]. Electrical Engineering, 2020, 21(3): 31-36, 58.
[22] 蘭征, 刁偉業, 曾進輝, 等. 含異構微源孤島微電網內虛擬同步發電機預同步控制策略[J]. 電力系統自動化, 2022, 46(19): 154-161.
Lan Zheng, Diao Weiye, Zeng Jinhui, et al. Pre-synchronization control strategy of virtual synchronous generator in islanded microgrid with heterogeneous distributed generators[J]. Automation of Electric Power Systems, 2022, 46(19): 154-161.
[23] 顏湘武, 崔森, 常文斐. 考慮儲能自適應調節的雙饋感應發電機一次調頻控制策略[J]. 電工技術學報, 2021, 36(5): 1027-1039.
Yan Xiangwu, Cui Sen, Chang Wenfei. Primary frequency regulation control strategy of doubly-fed induction generator considering supercapacitor SOC feedback adaptive adjustment[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 1027-1039.
[24] Wu Dan, Tang Fen, Dragicevic T, et al. Autonomous active power control for islanded AC microgrids with photovoltaic generation and energy storage system[J]. IEEE Transactions on Energy Conversion, 2014, 29(4): 882-892.
[25] Le H T, Santoso S, Nguyen T Q. Augmenting wind power penetration and grid voltage stability limits using ESS: application design, sizing, and a case study[J]. IEEE Transactions on Power Systems, 2012, 27(1): 161-171.
[26] Kim J, Lee S H, Park J W. Inertia-free stand-alone microgrid—part Ⅱ: inertia control for stabilizing DC-link capacitor voltage of PMSG wind turbine system[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4060-4068.
Novel Autonomous Power Balance Control for PMSG Based Wind Turbine in Stand Alone Operation
Lu Qiuyu1Dai Yaohui2Yang Yinguo1Han Jinlong2Liao Peng1
(1. Electric Power Dispatching and Control Center of Guangdong Power Grid Corporation Guangzhou 510600 China 2. School of Electrical Engineering Xi’an Jiaotong University Xi’an 710049 China)
Recently, the permanent magnet synchronous generator-based wind turbine (PMSG-based WT) have gained significant popularity in wind power applications. With the development of microgrids, the PMSG-based WTs are required to be operated in the stand-alone operation mode in some scenarios. The previous studies in stand-alone microgrids mainly focus on the phase-locked loop (PLL)-based controls for WT, which still require the external grid-forming power supplies. The recent studies for the stand-alone operation of PLL-free WTs were relatively complicated and difficult to adjust the parameters. They did not adequately discuss the coordination of grid side converter (GSC) and rotor side converter (RSC) of WT, nor did they consider the demand response in stand-alone operation mode (SAOM). To bridge these gaps, this paper proposed two advanced autonomous power balance control schemes for PMSG-based WT in SAOM.
In the first strategy, the GSC of WT controls the converter voltage as an ideal voltage source with the fixed modulation index and frequency, while the RSC of WT modifies the active power reference by controlling DC-link voltage through one PI controller. The main drawbacks of the first strategy are that the load demand response is not taken into consideration and it may not ensure the power synchronism of multi-WT in SAOM. Therefore, in the second strategy, the GSC of WT achieves grid-synchronization and inertia response utilizing the dynamic of DC-link voltage, while the RSC adjusts active power based on the DC-link voltage deviations to mimic the primary frequency control. Both proposed strategies can effectively ensure the independent operation of WT without PLL and external power supplies. Compared with the typical virtual synchronous generator (VSG) controls and other SAOM controls, the complexity of the proposed strategies is more reduced, and the control parameters are easy to tune, as they only require the measurement of DC-link voltage. Particularly, Strategy Ⅱ stands out by the energy-efficient property by using the reserved energy in DC capacitor for system inertia support and the load demand response to decrease the risks of WT tripping off. In order to improve the voltage profile of the second proposed scheme, an improved GSC control of WT via one simple PI controller for sustaining the point of common coupling (PCC) voltage during system disturbance is further proposed. Nonlinear simulations of one PMSG connected with several local loads considering various power system contingencies have been studied to verify the effectiveness of two proposed strategies.
The following conclusions can be drawn from the simulation analysis: (1) Both strategies can effectively ensure the stable operation of PMSG-based WT in tested stand-alone system. (2) StrategyⅠcan well stabilize the grid frequency and the DC-link voltage. But it requires high operation costs of WT and is not energy-saving in SAOM. (3) Strategy Ⅱ makes the alternation of DC-link voltage proportional to the grid frequency, which reduces the power balance burden of stand-alone WT by temporally absorbing or releasing the energy from DC capacitor during load changes. More importantly, Strategy Ⅱ stands out by fully utilizing the load demand response for fast power balance and decreasing the risk of WT tripping, which is more energy-efficient and is suitable for multi-WTs operation in SAOM.
Permanent magnet synchronous generator (PMSG), stand-alone operation, autonomous power balance control, inertia response, primary frequency control, energy-efficient property
陸秋瑜 女,1986年生,高級工程師,博士,研究方向為電力系統調度自動化等。E-mail:luqiuyu22@126.com(通信作者)
戴耀輝 男,1999年生,碩士研究生,研究方向為電力系統運行與控制。E-mail:dyh1499973952@stu.xjtu.edu.cn
TM711
10.19595/j.cnki.1000-6753.tces.221348
中國南方電網公司科技項目資助(036000KK52210042(GDKJXM20212057))。
2022-07-13
2022-12-30
(編輯 赫 蕾)

