自適應可分解部分重復碼的擴展構造

王甜甜,王汗青,孟 潔,余春雷,王曉峰

(1.海軍航空大學 航空基礎學院,山東 煙臺 264000;2.四川文理學院 智能制造學院,四川 達州 635000)

0 引 言

現如今,海量數據仍迅速膨脹,針對大數據的可靠安全存儲問題被廣泛重視。大規模分布式存儲系統成為當前存儲海量數據的有效途徑,因其具備可用性高、成本低、吞吐量高和可擴展等優勢[1]。由于系統中經常發生存儲節點故障的情形,為了使分布式存儲系統提供可靠的存儲服務,需要通過連接其他存活節點對故障節點進行修復。通常需要采取一定的冗余策略,以保證數據存儲的有效性和可靠性。主流的冗余策略是復制(Replication)[2]和糾刪碼(Erasure Codes)[3]。復制策略的存儲成本太大,在修復故障節點時糾刪碼的帶寬開銷較高。

針對復制策略和糾刪碼策略在數據存儲和故障修復中存在的局限性,通過將“網絡編碼”的思路引入分布式存儲系統中,Dimakis等人提出了再生碼(Regenerating Codes,RC)[4],降低了修復帶寬開銷和節點存儲開銷[5]。根據存儲—帶寬開銷權衡曲線上的最佳極值點,Rashmi等人提出了最小帶寬再生(Minimum Bandwidth Regeneration,MBR)碼和最小存儲再生(Minimum Storage Regeneration,MSR)碼[6]。但再生碼需要連接較多存活節點來修復故障節點。為了降低修復故障節點時的修復局部性,Papailiopoulos等人提出了局部性修復編碼(Locally Repairable Codes,LRC)[7],在局部修復組內對故障節點進行修復。結合RS碼與簡單的異或運算,Papailiopoulos提出了簡單再生碼(Simple Regenerating Codes,SRC)[8]。再生碼和LRC需要通過大量運算來修復故障節點,其修復過程中的計算復雜度較高,導致修復時間較長[9]。

為了保證修復故障節點時具有較低修復帶寬開銷,同時進一步提高修復效率,Ramchandran等人提出了一種實現對故障節點進行精確無編碼修復的MBR碼——部分重復(Fractional Repetition,FR)碼[10]。實際的分布式存儲系統是一種動態的隨機變化的環境,也就是說,存儲節點故障和部分數據丟失等情況隨時可能發生[11]。針對這一問題,朱兵提出了自適應FR碼[11],以使FR碼適用于動態分布式存儲系統。采用自適應FR碼的分布式存儲系統中,在節點中部分數據丟失并無法修復的情況下,通過簡單調整系統結構以滿足FR碼特性,無需重新配置存儲系統[12]。隨后,Oktay Olmez提出了可分解FR碼[13-15],并提出了基于組合設計的構造方法。可分解FR碼中每個平行類均存儲原文件大小的數據量,在部分節點故障的情況下,剩余平行類中存活節點仍滿足FR碼特性。Su Yisheng結合自適應FR碼與可分解FR碼的特性,提出了自適應可分解FR碼,并提出了基于仿射置換矩陣(Affine Permutation Matrices,APMs)與循環置換矩陣(Circulant Permutation Matrices,CPMs)的構造方法[16],有效適應了節點存儲容量和數據塊重復度在動態存儲系統中的隨機動態變化。為了使系統中存儲節點數和節點存儲容量易于擴展,朱兵提出了可擴展FR碼的顯式構造方法[17]。Krishna提出了具有非對稱參數的廣義部分重復(Generalized Fractional Repetition,GFR)碼,并建立了GFR碼與超圖的對應關系[18]。

基于上述研究基礎,該文在自適應可分解FR碼原始構造方案的基礎上,提出了利用超圖實現自適應可分解FR碼的擴展構造方法,實現FR碼在動態分布式存儲系統中的靈活擴展。當文件規模或分布式存儲系統規模發生變化時,根據超圖中邊和頂點對應于FR碼中節點和數據塊的關系,通過增加或刪除超圖中對應的邊和頂點,實現動態分布式存儲系統中自適應可分解FR碼的擴展構造。通過這種基于超圖的擴展構造方法,能夠擴展出給定參數范圍內的所有自適應可分解FR碼,該文列舉出了存儲節點數20以內自適應可分解FR碼的所有參數。自適應可分解FR碼與SRC和RS碼相比,在修復局部性和修復帶寬開銷方面具有一定優勢。

1 基礎知識

1.1 自適應可分解FR碼

在(n,k,d)分布式存儲系統中,假定節點存儲容量為α,從n個存儲節點中至少連接任意k個存活節點即可重構原文件,單節點故障需要至少連接d個存活節點實現修復,則滿足條件k≤d≤n-1,且d=α。

FR碼[10]:在(n,k,d)分布式存儲系統中,設定FR碼C=(Ω,N)由n個子集組成的集合N={N1,…,Nn}表示,其中,每個子集均由符號集Ω={1,…,θ}中元素描述,且符號集Ω中元素的重復度均為ρ,該FR碼亦可描述為(n,d,θ,ρ)FR碼[19]。該(n,d,θ,ρ)FR碼滿足以下條件:

(1)子集Ni(i=1,…,n)的大小均為d;

(2)符號集Ω中每個元素均屬于集合N中的ρ個子集;

(3)子集Ni和Nj(i≠j)最多包含符號集Ω中的一個元素;

(4)θρ=nd。

自適應FR碼[11]:在FR碼C=(Ω,N)中,如果?S?Ω,且由非空子集N0S,N1S,…,Nn-1S組成的集合也是一個FR碼C',則C為自適應FR碼。

當存儲系統中部分數據永久性故障而無法恢復時,原來的自適應FR碼C通過簡單調整得到新的FR碼C',以適應新的分布式存儲系統。

通過改變可分解FR碼中的平行類數,即可改變數據塊的重復度。由于每個平行類中的節點均存儲全部數據塊,因此重構原始文件可以通過下載任一平行類中的數據塊實現,進而修復故障節點。當FR碼中包含多個平行類時,即使刪除該故障節點所在的平行類,其余節點仍滿足FR碼特性。

自適應可分解FR碼同時滿足自適應FR碼和可分解FR碼的特性,能夠有效適應于動態分布式存儲系統[15]。

1.2 超 圖

超圖[20]:對于離散集合H=(V,E),其中V=(v1,…,vn)是離散元素的有限集合,E=(E1,…,Em)是V中各非空子集的集合,則超圖就是離散集合H=(V,E)。在超圖中,頂點的集合為V,邊的集合為E,任意非零數量的頂點連接成超圖的邊。

簡單超圖:超圖的邊集E=(E1,…,Em)中,如果滿足Ei?Ej,則i=j,即任意兩條邊Ei、Ej沒有包含關系,則該超圖為簡單超圖。

線性超圖:超圖的邊集E=(E1,…,Em)中,當i≠j時,|Ei∩Ej|≤1,即任意兩條邊Ei、Ej連接不超過一個共同頂點,則該超圖為線性超圖。

r-一致超圖:超圖的秩記為r(H)=maxj|Ej|,超圖的下秩記為s(H)=minj|Ej|,當滿足r(H)=s(H)時,超圖H稱為一致超圖。每條邊均連接r個頂點的超圖,簡記為r-一致超圖。

t-正則超圖:超圖H中,連接頂點vi(i=1,…,n)的邊數為頂點vi的度,凡所有頂點的度均相同的超圖稱為正則超圖[21]。每個頂點均由t條邊連接的超圖,簡記為t-正則超圖。

(r,t)-超圖:對于線性超圖,如果所有的邊均包含r個頂點,且所有頂點均存在于t條邊中,則稱為線性r-一致t-正則超圖,簡記為(r,t)-超圖。

子超圖:對于超圖H=(V,E),頂點子集A?V,其子超圖為HA=(A,{e∩A|e∈E∧e∩A≠?})。在原超圖的基礎上去掉某些頂點后的超圖,就是子超圖。

部分超圖:超圖H=(V,E)中,邊集E={ei|i∈Ie∧ei?V∧ei≠?}的索引集為Ie,對于I?Ie,該超圖的部分超圖為HI=(V,{ei|i∈I})。

2 自適應可分解FR碼的擴展構造

建立(d,ρ)-超圖與(n,d,θ,ρ)自適應可分解FR碼的對應關系,超圖中邊和頂點分別對應FR碼中存儲節點和數據塊。通過對(d,ρ)-超圖進行擴展,實現自適應可分解FR碼在動態分布式存儲系統中的擴展,而無需對系統進行重新配置。本節基于(d,ρ)-超圖,從存儲系統規模和存儲文件規模變化這兩個方面,對自適應可分解FR碼進行擴展構造,使擴展后的FR碼仍滿足自適應和可分解特性。

2.1 存儲系統規模變化

當存儲系統規模發生變化時,通過改變存儲節點數和數據塊重復度,即可對原自適應可分解FR碼進行擴展構造。

如果存儲系統規模減小,即存儲節點數n減小,假定節點存儲容量d和存儲文件規模(即數據塊數θ)均不變,為滿足FR碼的存在條件(即θρ=nd),則需要減小數據塊重復度ρ。因為FR碼中平行類的存儲節點與超圖的染色邊相對應,刪除(d,ρ)-超圖中對應染色邊,就能實現向(d,ρ-1)-部分超圖的擴展。根據(d,ρ-1)-部分超圖中邊和頂點對應于FR碼中節點和數據塊的關系,實現分布式存儲系統規模變化時的擴展。

圖1為(4,4)-超圖,圖2為對應的(16,4,16,4)自適應可分解FR碼。當存儲節點數減小為n=12時,為滿足θρ=nd,則減小數據塊重復度為ρ=3。在(4,4)-超圖基礎上,刪除染色邊{e13,e14,e15,e16},得到圖3所示(4,3)-部分超圖,對應得到圖4所示(12,4,16,3)自適應可分解FR碼。

圖2 (16,4,16,4)自適應可分解FR碼

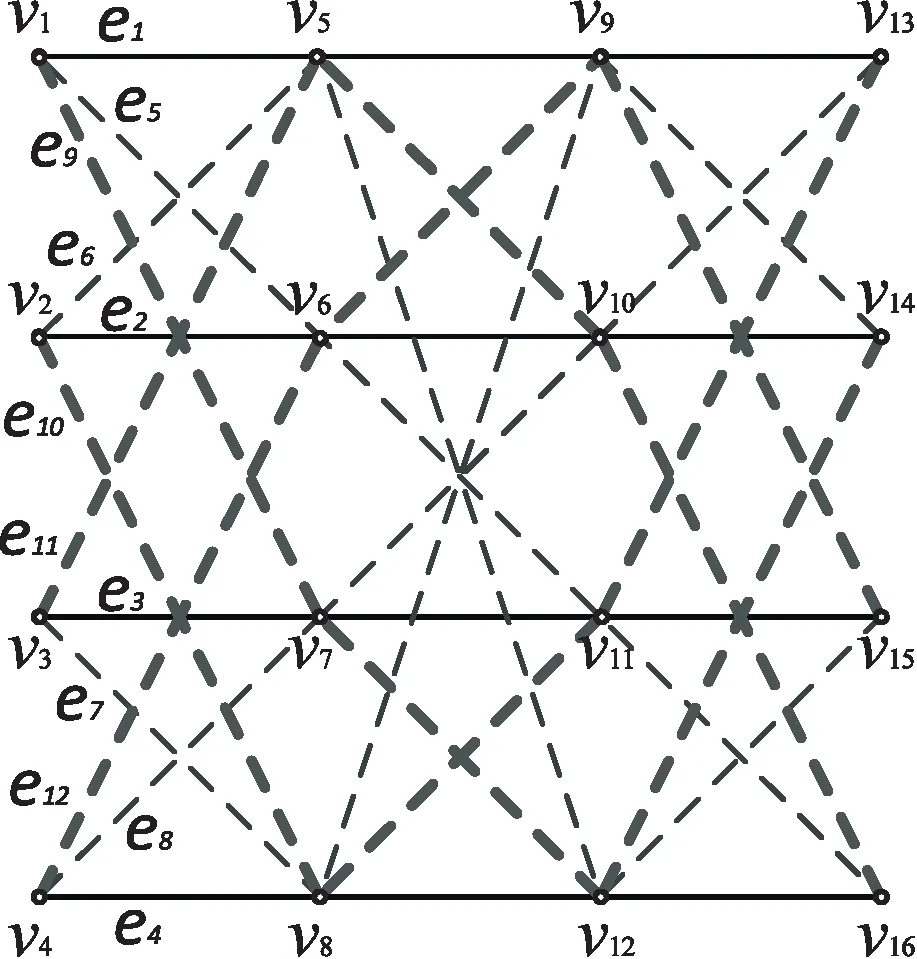
圖3 (4,3)-部分超圖

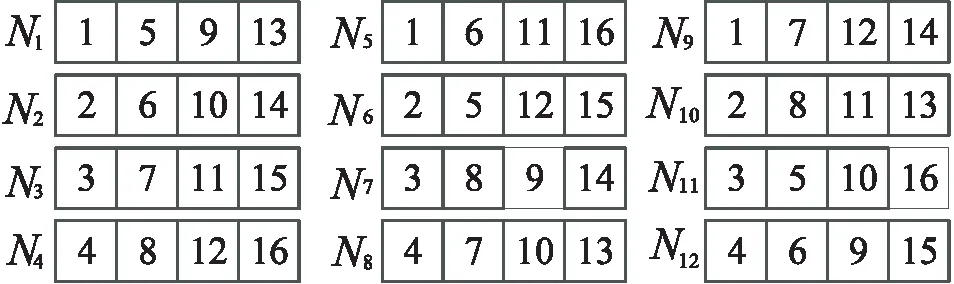
圖4 (12,4,16,3)自適應可分解FR碼

2.2 存儲文件規模變化

當存儲文件規模發生變化時,通過改變數據塊數和節點存儲容量,即可對原自適應可分解FR碼進行擴展構造。

如果存儲文件規模減小,假定數據塊大小不變,則數據塊數θ減小,存儲節點數n不變,為滿足FR碼的存在條件(即θρ=nd),保持數據塊重復度ρ不變,則需要減小節點存儲容量d。因為FR碼的數據塊與超圖的頂點相對應,刪除(d,ρ)-超圖中對應頂點,就能實現向(d-1,ρ)-子超圖的擴展。根據(d-1,ρ)-子超圖中邊和頂點對應于FR碼中節點和數據塊的關系,實現存儲文件規模變化時的擴展。

在圖4所示(12,4,16,3)自適應可分解FR碼的基礎上,當數據塊數減小為θ=12時,為滿足θρ=nd,則減小節點存儲容量為d=3。在圖3所示(4,3)-超圖基礎上,刪除頂點{v13,v14,v15,v16},得到圖5所示(3,3)-子超圖,對應得到圖6所示(12,3,12,3)自適應可分解FR碼。

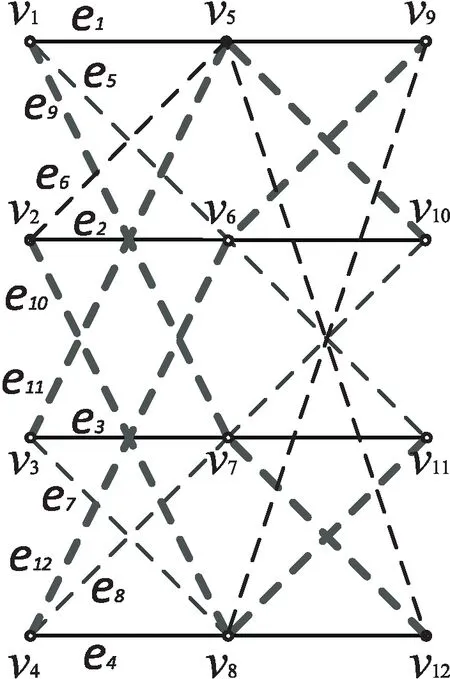
圖5 (3,3)-子超圖

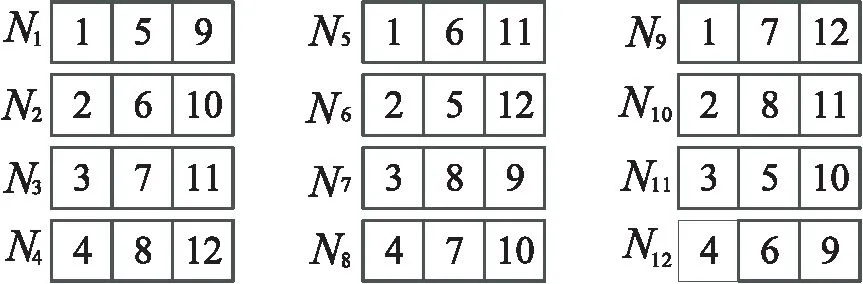
圖6 (12,3,12,3)自適應可分解FR碼

2.3 自適應可分解FR碼的參數范圍

利用(d,ρ)-超圖實現自適應可分解FR碼的擴展,能夠在給定參數范圍內構造全部自適應可分解FR碼。表1為自適應可分解FR碼在存儲節點數20個以內的全部(n,d,θ,ρ)參數。如表1所示,全部(n,d,θ,ρ)FR碼均可通過基于(d,ρ)-超圖的擴展實現。例如,針對存儲節點數n=8,通過存儲文件規模變化時的擴展方法,能夠實現(8,2,8,2)自適應可分解FR碼向(8,3,12,2)和(8,4,16,2)自適應可分解FR碼的擴展。

表1 (n,d,θ,ρ)自適應可分解FR碼的參數范圍 (n≤20)

3 性能分析

分布式存儲系統在修復故障節點時的兩個重要性能是修復局部性和修復帶寬開銷。本節從這兩個方面分析自適應可分解FR碼的性能,并對比最常見的SRC和RS碼,通過Matlab仿真給出這三種編碼方式的性能對比。

3.1 修復局部性

在分布式存儲系統中,假設原文件大小為M,存儲節點數為n,重構原文件需要至少連接任意k個存活節點。(n,k)RS碼中,只要故障節點數小于等于n-k,均需要連接k個存活節點的數據解碼重構原文件,再編碼恢復故障節點數據,則修復局部性為k。(n,k,f)SRC中,原文件由f個采用(n,k)RS編碼的子文件組成,通過連接2f個存活節點能夠修復單節點故障,則單節點故障的修復局部性為2f;當兩節點同時故障時,需要連接k個存活節點解碼重構原文件后進行故障修復,則兩節點同時故障的修復局部性為k。(n,d,θ,ρ)自適應可分解FR碼中,當單節點故障時,需要連接任一平行類的d個存活節點下載相應數據塊,則修復局部性為d。當兩節點同時故障時,若重復度ρ>2,通過任一平行類的min{n/ρ,2d}個存活節點下載相應數據塊,則修復局部性為min{n/ρ,2d};若重復度ρ=2,且兩個故障節點存儲相同數據塊,連接任意k個存活節點重構原文件進行故障修復,則修復局部性為k;若重復度ρ=2,且兩個故障節點沒有存儲相同數據塊,需要連接n/ρ或2d個存活節點,則修復局部性為n/ρ或2d。

設定(n,k,f)SRC和(n,k)RS碼的存儲節點數為n=12,重構原文件需要至少連接任意k=9個存活節點。SRC中原文件由f=3個子文件組成,每個子文件均采用(12,9)RS編碼。為便于性能分析,設定(n,d,θ,ρ)自適應可分解FR碼外部采用(12,9)MDS編碼,其編碼數據塊的數目θ=12,數據塊重復度ρ=3,因此節點存儲容量為d=3。如圖7所示,相比于(12,9,3)SRC和(12,9)RS碼,外部采用(12,9)MDS編碼的(12,3,12,3)自適應可分解FR碼在修復局部性上具有較大優勢。

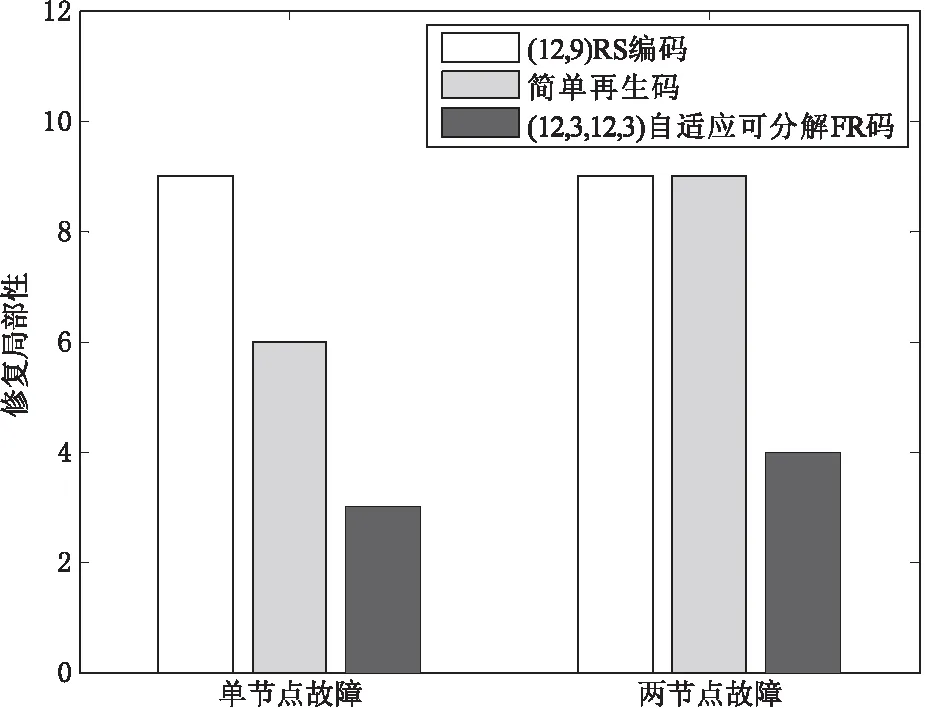
圖7 修復局部性

3.2 修復帶寬開銷

(n,k)RS碼中,只要故障節點數小于等于n-k,均需要連接k個存活節點并分別下載M/k的數據量,則修復帶寬開銷為M。(n,k,f)SRC中,當單節點故障時,下載f個數據塊并進行異或運算能夠修復一個故障數據塊,由于每個節點存儲f+1個數據量為M/fk的數據塊,則單節點故障的修復帶寬開銷為(f+1)M/k;當兩節點同時故障時,同(n,k)RS碼一樣,修復帶寬開銷為M[22]。采用(θ,j)MDS編碼的(n,d,θ,ρ)自適應可分解FR碼,每個數據塊的數據量為M/j,當單節點故障時,通過d個存活節點下載相應故障數據塊即可,則單節點故障的修復帶寬開銷為Md/j。當兩節點同時故障時,若重復度ρ>2,這兩個故障節點最多存儲一個相同數據塊,則修復帶寬開銷為M(2d-1)/j或2Md/j;若重復度ρ=2,且兩個故障節點存儲相同數據塊,需要重構原文件進行故障修復,則修復帶寬開銷為M;若重復度ρ=2,且兩個故障節點不包含相同數據塊,只需要從存活節點中下載相應故障數據,則修復帶寬開銷為2Md/j。

在3.1節(12,9,3)SRC、(12,9)RS碼和(12,3,12,3)自適應可分解FR碼的基礎上,設定原始文件大小M=1 000 Mb。如圖8所示,相比于(12,9,3)SRC和(12,9)RS碼,外部采用(12,9)MDS編碼的(12,3,12,3)自適應可分解FR碼,在修復帶寬開銷上具有較大優勢。

4 結束語

針對動態分布式存儲系統中FR碼的靈活擴展問題,提出一種利用超圖實現自適應可分解FR碼的擴展構造方法,能夠實現當文件規模變化和存儲系統規模變化時的擴展構造。具體地,建立(d,ρ)-超圖與(n,d,θ,ρ)自適應可分解FR碼的對應關系,在原FR碼構造和原超圖結構的基礎上,通過增加或刪除超圖中邊和頂點,實現對動態分布式存儲系統中自適應可分解FR碼的擴展構造。基于這種方法,能夠擴展構造出給定參數范圍內所有自適應可分解FR碼。自適應可分解FR碼相比于SRC和RS碼,具有較優的修復局部性和修復帶寬開銷。