“線性規劃”復習的“三把鑰匙”

■四川省綿陽外國語學校 李學軍

從近幾年的高考試卷來看,線性規劃考點的試題多出現在選擇題和填空題中。考查方向主要集中在三個方面:一是求目標函數的最值;二是根據目標函數的最值求參數的取值范圍;三是運用“線性規劃”思想解決綜合性問題。考查方向的三類問題的一般解法就是“線性規劃”問題的“三把鑰匙”。以下舉例說明在高考復習備考中如何獲取這“三把鑰匙”。

一、掌握求目標函數最值的基本方法,取得“入門鑰匙”

1.求線性目標函數的最值

例1若實數x,y滿足約束條件求z=2x+y的取值范圍。

解析：根據約束條件作出可行域,如圖1所示。

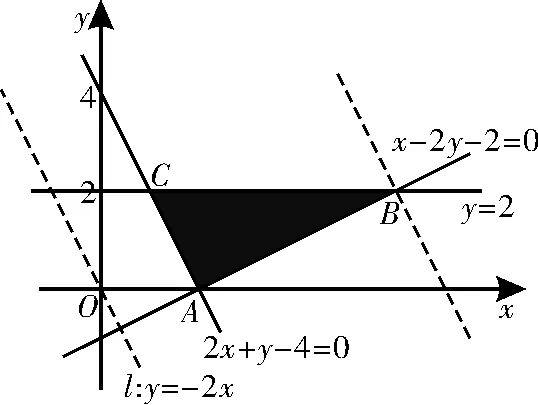
圖1

目標函數的特征直線l與AC:2x+y-4=0 平行,易得點A(2,0),聯立可得點B(6,2)。平移直線l經過點A時,z取最小值,zmin=2×2+0=4;平移直線l經過點B時,z取最大值,zmax=2×6+2=14。所以z的取值范圍為[4,14]。

歸納：求線性目標函數最值的一般步驟:①正確作圖表示可行域,注意邊界的虛實;②將目標函數變形為斜截式y=-2x+z;③找到目標函數的特征直線;④在目標函數的斜截式方程中,分析縱截距最大或最小時與目標函數取最大或最小值的對應關系,從而確定要計算的最優解;⑤計算最優解,并代入目標函數求出目標函數的最值。

變式1已知實數x,y滿足約束條件

(1)求使目標函數z=3x+y取最小值的最優解對應的點(x,y)。

(2)求使目標函數z=x+y取最小值的最優解對應的點(x,y)。

分析：(1)如圖2,目標函數z=3x+y化為y=-3x+z,其特征直線y=-3x的傾斜角小于可行域的邊界直線AC的傾斜角,故使z=3x+y取最小值的最優解對應的點為C(1,2)。

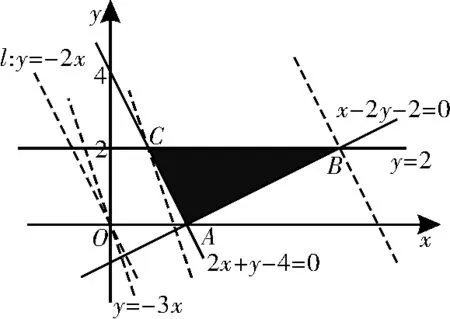
圖2

(2)如圖3,目標函數z=x+y化為y=-x+z,其特征直線y=-x的傾斜角大于可行域的邊界直線AC的傾斜角,故使z=x+y取最小值的最優解對應的點為A(2,0)。

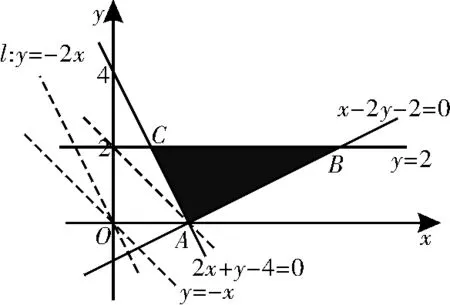
圖3

歸納：①特征直線與邊界直線的傾斜角的大小關系,直接影響最優解的位置;②目標函數的最優解有可能不止一個。

變式2若實數x,y滿足約束條件求x-2y的取值范圍。

分析：根據約束條件作出可行域,如圖4所示。令z=x-2y,則,易得點A(2,0),聯立可得點C(1,2)。平移直線l:經過點A時,z取最大值,zmax=2-2×0=2;平移直線l經過點C時,z取最小值,zmin=1-2×2=-3。

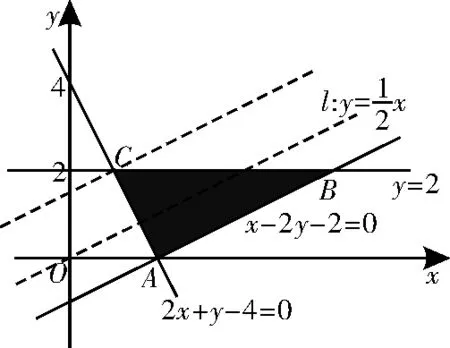
圖4

所以x-2y的取值范圍為[-3,2]。

歸納：目標函數的最值要與截距的最值正確對應,避免在最優解的選擇上出現錯誤。

2.求非線性目標函數的最值

例2若實數x,y滿足約束條件的取值范圍。

解析：根據約束條件作出可行域,如圖5 所示。表示可行域內的點與定點D(6,1)連線的斜率,易得邊界直線AD的斜率=,根據傾斜角的變化范圍可知的取值范圍為。

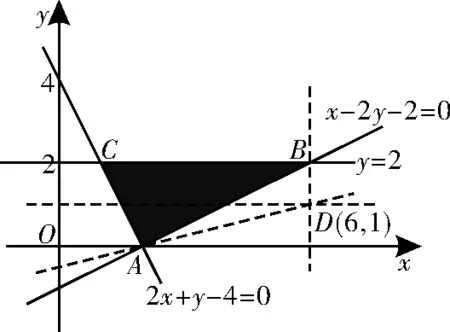
圖5

歸納：求非線性目標函數最值的一般步驟:①正確作圖表示可行域,注意邊界的虛實;②把目標函數抽象成可行域內的點滿足的幾何(如斜率、距離等)要素;③根據幾何要素進行動態分析,找到滿足條件的可行解的邊界;④根據可行解區域范圍及邊界的幾何要素的取值,寫出目標函數的最值。

變式1若實數x,y滿足約束條件的取值范圍。

分析：根據約束條件作出可行域,如圖6所示。表示可行域內的點與定點E(3,4)連線的斜率,計算邊界直線的斜率得kCE=1,,受傾斜角范圍的影響,斜率(即目標函數值)的范圍不連續,故的取值范圍為。

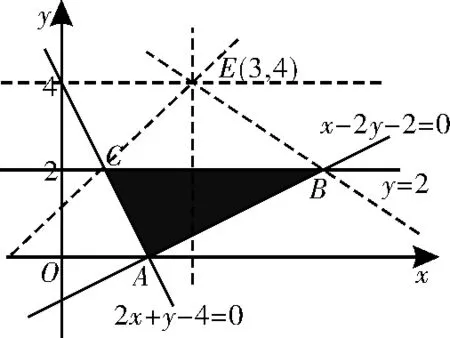
圖6

變式2若實數x,y滿足約束條件求|3x+4y-3|的取值范圍。

分析：根據約束條件作出可行域,如圖7所示。|3x+4y-3|可化為,其幾何意義是可行域內的點到定直線3x+4y-3=0 的距離的5 倍,其最小值為=3,最大值為=23,故|3x+4y-3|的取值范圍為[3,23]。

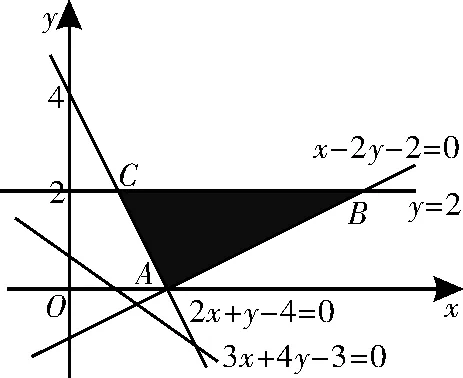
圖7

歸納：①抽象為斜率的非線性目標函數,應根據傾斜角可行的變化范圍對應出斜率的取值范圍,該范圍不一定是一個連續區間。②個別非線性目標函數在進行變形(配方、分離常數、配湊)后,可以抽象出斜率、距離等幾何要素,故也可以用線性規劃思想求其值域。

二、學會根據目標函數最值求參數的值,獲得“進階鑰匙”

1.參數出現在約束條件中

例3已知實數x,y滿足約束條件其中a∈R,若點(x,y)構成的圖形面積為6,則實數a的值為_____。

解析：如圖8所示,直線2x+ay-4=0經過定點A(2,0),由題意知△ABC的面積為6,即|BC|=6,由故點B(6,2),于是點C的坐標為(0,2),把C(0,2)代入2x+ay-4=0,解得a=2。

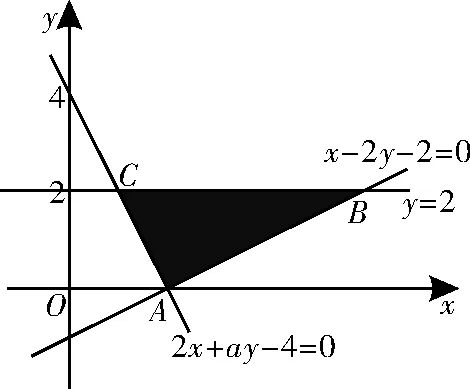
圖8

歸納：約束條件中含有參數的分析思路:①分析含有參數的邊界直線所過的定點,及參數對此邊界直線位置的影響;②分析題目中與參數有關的數量關系,確定求解參數的方法。

2.參數出現在目標函數中

歸納：目標函數中含有參數的分析思路:①將目標函數化為斜截式,分析參數對目標函數的位置及最優解的影響;②根據目標函數取值的特征,建立參數的數量關系求參數的值。

三、掌握“線性規劃”綜合性問題的分析方法,獲得“通關鑰匙”

例5設f(x)是定義在R 上的增函數,對任意的x都有f(1-x)+f(1+x)=0恒成立,若實數m,n滿足不等式組則m2+n2的取值范圍為_____。

解析：由f(1-x)+f(1+x)=0 得f(1-x)=-f(1+x)。

由f(m2-6m+23)+f(n2-8n)＜0得f(m2-6m+23)＜-f[1+(n2-8n-1)]。

所以f(m2-6m+23)＜f[1-(n2-8n-1)]=f(2-n2+8n)。

因為f(x)是R上的增函數,所以m2-6m+23＜2-n2+8n,即(m-3)2+(n-4)2＜4,所以已知約束條件可轉化為

可行域是以(3,4)為圓心,2為半徑的圓的右半部分(不含圓周和直徑),如圖10 所示,目標函數m2+n2表示原點到可行域內的點的距離的平方。

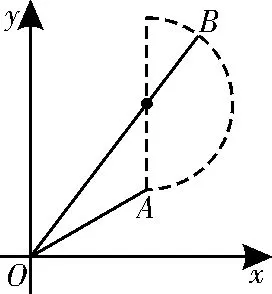
圖10

所以(m2+n2)min=|OA|2=32+22=13;(m2+n2)max=|OB|2=。

由于不含圓周和直徑,故m2+n2的取值范圍為(13,49)。

歸納：①注意挖掘題目中隱含的約束條件(二元一次不等式組);②靈活應用線性和非線性目標函數最值的求法,解決實際問題。

變式若函數f(x)=x2+1 的定義域為[a,b],值域為[1,5],則在平面直角坐標系內,點(a,b)與兩坐標軸圍成的圖形的面積為_____。

分析：由函數f(x)=x2+1的圖像(圖略)知a,b需滿足所以點(a,b)與兩坐標軸圍成的圖形是邊長為2的正方形,故面積為4。