哈密頓量誘導的量子演化速度*

董珊珊 秦立國 劉福窯 龔黎華 黃接輝?

1) (上海工程技術大學數理與統計學院,上海 201620)

2) (上海工程技術大學電子與電氣學院,上海 201620)

在研究量子態的演化問題時,量子演化速率往往定義為量子初態與其演化態之間的態距離隨時間的變化率.本文將量子演化的基本理論與線性代數方法相結合,通過量子態演化的路徑距離來研究量子系統的演化.量子幺正演化系統中,量子演化算符包含了量子演化的路徑信息,路徑距離的大小則決定于演化算符本征值的幅角主值分布.由量子態演化的路徑距離隨時間的變化率而得到的量子瞬時演化速率則正比于系統哈密頓量的最大與最小本征值之差.作為應用之一,利用量子演化的路徑距離及哈密頓量誘導的瞬時演化速率,可以給出量子演化新的時間下限.此時間下限只與系統的演化算符及哈密頓量有關,而與量子初態的具體形式無關,這與量子系統真實演化時間所具有的性質一致.嚴格的理論證明以及兩個演化實例的數值結果均表明,在 [0,π/(2ωH)] 時間范圍內,本文給出的演化時間下限與真實演化時間重合,是真實演化時間的準確預測.通過量子演化的路徑距離及相應演化速率來研究量子系統的演化,為相關問題的解答提供了新的思路和方法.

1 引言

量子態的演化速度是量子理論中的基本問題[1–3].隨著量子信息科學在近二三十年的蓬勃發展,量子態的演化速度再次引起物理學工作者的高度重視,因為它關系到量子計算的算力[4,5]、量子信息轉換率[6–8]、量子測量的測量精度[9–11]以及量子電池的充電量[12,13]等.在研究量子系統的演化問題時,量子演化速度往往定義為量子初態與其演化態之間的“距離”隨時間的變化率,這使得量子演化速度的計算不但與量子系統的哈密頓量有關,還與量子系統所處的狀態有關.但可以從另外一個角度來看量子態的演化問題.量子系統的演化遵循薛定諤方程為簡單起見,接下來設定 ?=1 .若不考慮系統耗散,則系統初態 |ψ0〉可以通過一個幺正算符Ut與其t時刻的演化態 |ψt〉關聯: |ψt〉=Ut|ψ0〉,而這個幺正算符完全由系統的哈密頓量及演化時間t決定:其中,T為時序算符,其依據時段先后對哈密頓量所對應的演化算符進行排序,先作用的哈密頓量所對應的演化算符排在幺正演化算符連乘形式的右側.這意味著,非耗散量子系統中,量子態的演化規律包含在幺正算符Ut中,不同量子初態可以看作量子系統演化的不同初始條件.如果能提取幺正算符Ut中所包含的“路徑”信息,那么這個路徑所包含的演化距離,以下簡稱為路徑距離,隨時間的變化率可以用來定義量子演化的瞬時速率.不難推斷,通過這個方式定義的量子演化速率取決于量子系統的哈密頓量,而與系統所處的量子態無關,這個性質與經典物理學中質點運動的瞬時速率是一致的.在經典物理學中,一個質點的運動狀態滿足牛頓第二運動定律:F=ma.只要給定質點運動的初始狀態,則其所受外力完全決定質點此后的運動狀態,包括其速度和位置等.其中,質點運動的瞬時速度定義為位移矢量隨時間的變化率.相應地,質點運動的瞬時速率等于路程隨時間的變化率,本質上,其大小取決于質點的初速度及其所受合外力,而與質點所處的位置無關.

基于量子系統的演化算符,本文定義了量子態演化的路徑距離,此路徑距離僅取決于演化算符本征值的輻角主值.可以證明,量子演化的路徑距離是所有量子初態與其量子演化態之間距離的上限.演化算符本征值的輻角主值分布隨時間的變化決定了量子演化的瞬時速率,其值正好等于系統哈密頓量最大與最小本征值差值的一半.作為應用之一,給出了量子系統真實演化時間的又一個下限,文中的理論證明及實例均表明,此時間下限在一個特定范圍內,與真實演化時間完全重合,是對量子系統真實演化時間的精準預測.

2 量子演化算符包含的路徑距離

在經典物理的運動學中,如果一個質點一直沿某個方向作直線運動,那么它所經歷的路程等于質點始末位置的距離,除此之外,質點所經歷的路程都大于質點始末位置的距離.以此為借鑒,定義量子演化算符Ut所包含的路徑距離,使其不小于通過Ut關聯起來的所有量子態對{ρ0,ρt}之間的態距離:

式中,Tr|·| 表示矩陣本征值的絕對值之和.而一個矩陣A的本征值的絕對值等于矩陣AA?或A?A本征值的算術平方根,這意味著,一個矩陣左乘或者右乘任意幺正矩陣都不會改變其本征值的絕對值.注意到V及Ut?均為幺正矩陣,故(2)式可改寫為

眾所周知,兩個量子態間的保真度在幺正變換下是保持不變的.我們總可以選擇合適的幺正變換,使得量子初態ρ0的本征態過渡到演化算符Ut的本征態上面的Uhlmann 保真度過渡為

接下來根據演化算符Ut本征值的輻角主值{?j}的分布,來確定上面的Uhlmann 保真度的最小值.毫無疑問,如果鎖定{?j}中絕對值最大的相位,比如?M≡max{|?j|},并忽略(4) 式中求和結果中的虛部,那很容易可得到Uhlmann 保真度的一個下限:

通過以上方式得到的Uhlmann 保真度下限 cos(?M) 并不能保證其緊湊性.注意到

其中,?0可以為任意位相常量,則{|?j-?0|}的最大值可以用來計算?M.同時,為了保證所得到的Uhlmann 保真度下限的緊湊性,我們又必須選取合適的?0,使得?M盡量小,所以?M定義為

為了讓相關討論更直觀,我們把輻角主值{?j}的分布在一個極坐標系的單位圓中表示出來.N維量子系統中,量子演化算符Ut有N個本征值,其輻角主值與單位圓中N條半徑的極角相對應,此單位圓的圓心取為極坐標系的極點.

現在我們通過以下4 步來找出(6)式中的目標?0及相應的?M.

1) 在以上單位圓與輻角主值{?j}相對應的N條半徑中,找出相鄰且夾角最大的兩條半徑.如果輻角主值{?j}按升序排列,那相鄰兩條半徑之間的夾角為

在圖1 中,夾角最大的兩條半徑為OC和OD,這兩條半徑對應的輻角主值為?3和?4.

圖1 在極坐標系的單位圓中,不同半徑的極角與演化算符本征值的輻角主值相對應.具有最大夾角的兩相鄰半徑,其夾角平分線的反向延長線的極角即為 ?0 取值,而 ?M 則為此反向延長線與前述兩相鄰半徑的夾角.?M 也有如下等效理解: 演化算符本征值的每個輻角主值與一個半徑對應,找到能覆蓋所有半徑的最小扇形,此最小扇形的圓心角的一半即為目標 ?M 值Fig.1.In the polar coordinate system,the polar angle of a radius in the unit circle corresponds to the principal argument of an eigenvalue of the evolution operator.The angular bisector of two neighboring radii,which form the largest included angle among all neighboring radii,is the reverse extension line of the radius with polar angle ?0 ,and?M is equal to half the largest included angle among all neighboring radii.Equivalently speaking,the principal argument of each eigenvalue of the evolution operator corresponds to a radius in the unit circle.If we find out the smallest sector in this unit circle to cover all radii mentioned above,?M is then equal to half the sector angle.

2) 若{Dj}中的第k個為最大值,即Dk=max{Dj},將其所對應的兩條半徑的極角標記為?+和?-,則:

3){Dj}中值最大的那個夾角的角平分線的反向延長線的極角即對應方程(6)中目標位相?0(見圖1 中的半徑OP),即其中“±” 二選其一,使得?0限定在 (-π,π] 范圍內.

4)?0與?+和?-所對應半徑間的夾角相同,這個夾角大小就是方程(6)中?M值,

通過這個方式得到的?M值有如下直觀解釋: 在以上單位圓中畫一個能覆蓋輻角主值{?j}所對應N條半徑的扇形,那么滿足這個條件的最小扇形的圓心角的一半即為方程(6)中?M值.這個最小扇形的對稱軸對應方程(6)中的?0位相.

基于此?M而得到 的Uhlmann 保真度下限,F(ρ0,ρt)≥cos(?M),相比F(ρ0,ρt)≥cos(max{?j})顯然更緊湊,因為不等式?M≤max{|?j|}始終成立.保真度的反余弦值,即Bures 角度,可以用來度量兩個量子態之間的態距離.因此把?M作為量子演化算符Ut所包含的路徑距離:

既然 cos(?M) 是Uhlmann 保真度的下限,可以得出如下結論: 量子演化算符Ut所包含的路徑距離不小于通過其連接起來的任意量子態對之間的Bures 角.通俗點講,就是量子態與其演化態之間的距離不大于演化過程中的路徑距離.這與經典物理中,一個質點運動軌跡上任意兩點之間的距離不大于這兩點之間路程的結論相一致.

3 哈密頓量誘導的瞬時演化速率

基于以上對量子演化算符Ut所包含的路徑距離的定義,來計算量子系統演化時的瞬時速率.在一個不含時非耗散量子系統中,量子系統從t時刻演化到 (t+dt) 時刻( dt→0) 所對應的演化算符為Udt=exp(-idt) .不含時哈密頓量的本征值為實數,本文采用D{λ}表示哈密頓量最大本征值與最小本征值的差值,D{λ}≡λmax-λmin.不難得出,當 dt→0 時,演化算符為Udt的本征值的輻角主值即 為哈密頓量本征值的 (-dt) 倍,并且均為小量.所以這些輻角主值中,相鄰輻角主值夾角的最大值為:max{Dj}=2π-dt(λmax-λmin)=2π-D{λ}dt.根據(10)式,演化算符Udt所包含的路徑距離為由此可得到量子系統在哈密頓量作用下的瞬時演化速率:

其中,λmax和λmin分別為哈密頓量的最大和最小本征值.由此可得出結論: 不含時哈密度量誘導的瞬時演化速率僅取決于哈密頓最大與最小本征值的差值.

如果以量子初態為基準,則量子系統的演化態與此量子初態之間的路徑距離隨時間的變化率必然以上面得到的瞬時演化速率為上限.因此,在一個不含時量子系統中,量子系統從初態演化到目標態所需的時間有一個下限:

早在20 世紀上半葉,Mandelstam 和Tamm[1]研究了一個量子純態自由演化到與其正交的量子態所需的最短時間,τMT=π/(2ΔE) ,ΔE是量子系統的能量帶寬.這個結論說明,若以量子態之間的態距離為距離量度,量子系統的能量帶寬與量子態演化速率直接相關.相關研究很快被推廣到一般情形,當目標態與初態不正交時,在這兩個量子態之間自由演化的Mandelstam-Tamm 時間下限是[19,20]:

4 舉例和討論

根據這些信息,不難得到t時刻的演化態與初態之間的態距離,即Bures 角為

進而可用(13)式來估算從初態到t時刻演化態之間的Mandelstam-Tamm 時間下限τMT.同 時,在演化時間t∈[0,π/(2ωH)] 范圍內,由(10) 式可以給出演化算符Ut所包含的路徑距離:d(Ut)=而由(11)式得到的哈密頓量所誘導的演化速率為所以,在演化時間t∈[0,π/(2ωH)] 范圍內,采用(12)式能準確預測量子系統的真實演化時間:τH=t,這一結論與上面討論的二維純態情形相同.值得關注的是,這一結論不依賴于量子初態中cj參數的選擇.實際上,可以把此結論推廣到一般情形: 在幺正演化系統中,基于哈密頓量誘導的量子演化速率ωH而得到的演化時間下限τH,在∈[0,π/(2ωH)] 范圍內,其預測值與系統真實演化時間完全相等.

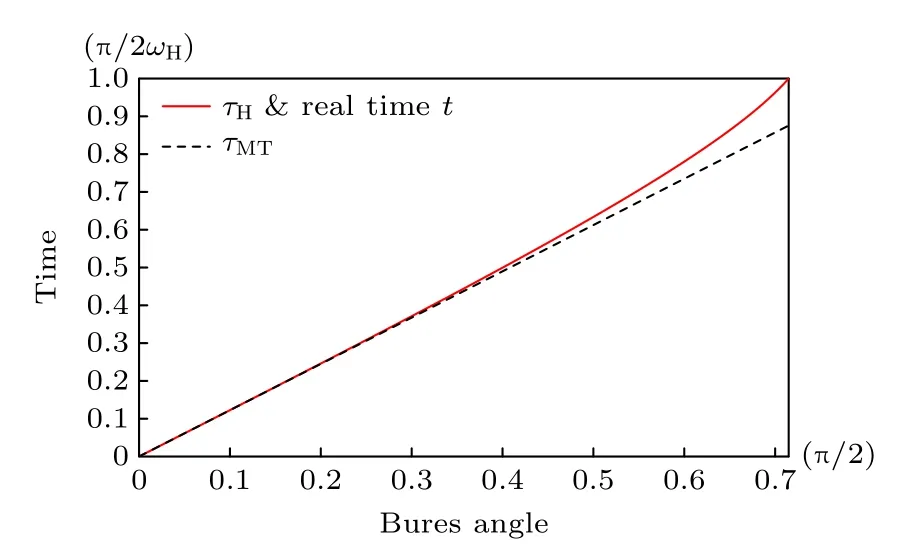
圖2 三能級量子純態 |ψ0〉 在t ∈ 時間范圍內的自由演化過程中,本文提出的演化時間下限τH始終與真實演化時間t重合,見紅色實線.而Mandelstam-Tamm 時間下限位于真實演化時間曲線的下方,見黑色短劃線Fig.2.During the evolution of a qutrit prepared in a pure state |ψ0〉,the lower bound of the evolution time proposed here meets the real evolution time perfectly in the range t ∈.The curve of the Mandelstam-Tamm bound is below the curve of the real evolution time,see the black dashed line.

本文提出的演化時間下限τH只依賴于系統的演化算符及哈密頓量誘導的演化速率,而與量子初態無關,這個性質也是其與Mandelstam-Tamm時間下限的又一重要區別.現在研究以上例子中的量子純態和一個量子混合態其中在相同哈密頓量=Diag(1 2 4) 作用下的演化速率,并把本文提出的時間下限τH與Mandelstam-Tamm 時間下限作對比.在圖3 中以真實的演化時間t為橫坐標,畫出了以上純態和混合態演化特例中時間下限τH與Mandelstam-Tamm 時間下限的變化曲線.可以看到,無論系統的初態是純態還是混合態,只要系統的哈密頓量相同,那么系統的演化速度就相同,在t∈[0,π/(2ωH)] 演化時間范圍內,本文提出的演化時間下限τH與真實的演化時間t完全重合,這一結論對純態和混合態的演化都成立.而無論是量子純態 |ψ0〉,還是混合態ρ0的演化,若用Mandelstam-Tamm 下限來估算量子系統的真實演化時間,其值都比真實值小.相比較而言,量子混合態ρ0的演化過程中,Mandelstam-Tamm 下限與真實時間的誤差比量子純態的演化過程中的誤差大,這與文獻[21,22]得到的結論相一致.

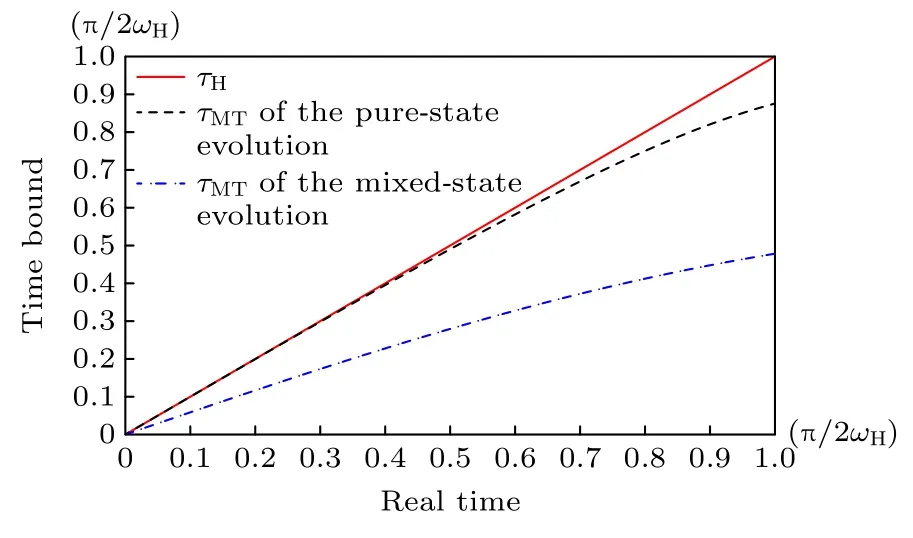
圖3 在相同的哈密頓量作用下,三能級量子純態 |ψ0〉 和混合態 ρ0 在演化 過程中,依據本 文提出 的時間下限 τH 在[0,π/(2ωH)]范圍內與真實演化時間相等,見紅色實線.量子純態 |ψ0〉 演化過程中的Mandelstam-Tamm 時間下限小于真實演化時間,見黑色短劃線.對混合態 ρ0 的演化而言,其Mandelstam-Tamm 時間下限與真實演化時間的偏差最大,見藍色點線Fig.3.During the evolution of a qutrit prepared in a pure state |ψ0〉 and in a mixed state ρ0,governed by the same Hamiltonian,the lower bound of the evolution time proposed here meets the real evolution time perfectly in the range t ∈[0,π/(2ωH)],see the black dashed line.In the evolution of the mixed state ρ0,the Mandelstam-Tamm bound is deviated from the real evolution time substantially,see the blue dotted line.

5 結論

量子態的演化速度關系到很多量子信息處理過程的速度,是量子信息相關領域的重要課題,正吸引越來越多的關注[23–30].在以往的研究中,量子系統的演化速度往往定義為量子初態與其量子演化態之間的態距離隨時間的變化率.實際上,量子態在幺正系統中的演化過程完全體現在其演化算符中,量子系統演化的距離可以通過演化算符來量化.從量子基本原理出發,采用線性代數的方法定義了量子幺正系統的路徑距離,發現其只與演化算符的本征值的輻角主值分布有關.換句話說,量子系統的路徑距離只取決于系統的哈密頓量及演化時間,而與量子態的具體形式無關.這一性質與不同量子態在相同哈密頓量作用下的演化特性吻合:在相同哈密頓量相同時間的作用下,不同量子態經歷相同的演化算符作用,可視為經歷了相同的演化“路徑”,但不同量子初態與其量子演化態之間的態距離是不一樣的.

基于以上的演化路徑距離,量子系統的瞬時演化速率ωH可定義為瞬時路徑距離對時間的變化率,其值正好等于哈密頓量最大與最小本征值之差的一半.哈密頓量誘導的瞬時演化速率表示量子系統演化的快慢,從而決定了量子系統從一個量子態到一個目標態之間的演化時間.如果量子系統以哈密頓量誘導的瞬時演化速率ωH沿測地線向某目標態演化,則量子初態與目標態之間的路徑距離與瞬時演化速率的比值為真實演化時間的一個下限.本文在理論上證明:在[0,π/(2ωH)] 演化時間內,以上演化時間下限與真實演化時間完美重合,是真實演化時間的精準預測.而廣泛應用的Mandelstam-Tamm 時間下限只有在二維特殊純態情況下才與真實演化時間重合.采用二維量子比特系統及三維qutrit 系統中量子純態和量子混合態的演化實例對相關結論進行了驗證.通過量子演化的路徑距離及相應演化速率來研究量子系統的演化,為相關問題的解答提供了新的思路和方法.