自旋混合庫珀對引起的Josephson 電流*

孟豪 吳修強

1) (陜西理工大學物理與電信工程學院,漢中 723001)

2) (鹽城工學院物理系,鹽城 224051)

通過求解Bogoliubov-de Gennes 方程研究一維S/FL-F-FR/S 結中Josephson 電流的輸運特性,其中S 和F 分別是超導體和鐵磁體,FL,R 是左右兩側具有非共線磁矩的界面層.研究發現,FL 和FR 界面能夠產生自旋混合和自旋翻轉效應,該效應能夠將S 內一部分自旋單重對轉化為F 內自旋相同的三重對.對于短S/FL-F-FR/S結,F 層內同時存在自旋單重對和自旋相同的三重對.于是,隨著鐵磁交換場和界面磁矩偏轉角度差的增加,臨界電流在一個基準面上振蕩.若F 轉變為半金屬,則F 內僅剩自旋相同的三重對,臨界電流的振蕩特征消失.此外,FL 和FR 界面還能起到普通勢壘的作用.這將導致臨界電流隨著鐵磁厚度的增加展現出雙重振蕩行為,其中長波振蕩源于鐵磁體內自旋單重對的位相變化,短波振蕩是由自旋單重對和自旋相同的三重對經過兩個界面勢壘時的共振隧穿效應引起的.

1 引言

隨著自旋電子學的發展以及信息存儲和數據傳輸量子器件的不斷開發和利用,近年來人們對超導(S)/鐵磁(F)異質結中超流的產生、輸運和操控有極大的興趣[1?8].根據Bardeen-Cooper-Schrieffer(BCS)理論可知,金屬超導體內的Cooper(庫珀)對是自旋單重對,它由自旋和動量都相反的兩個電子組成.與此相反,鐵磁體內的強交換相互作用會使電子自旋趨于同向.因此,超導與鐵磁間的相互競爭會引起一系列有趣的現象.當前計算機的計算和硬盤讀寫過程僅僅利用了電子的電荷特性,為了提高計算速度和計算精度,人們很早就希望將電子的自旋自由度引入到量子計算和存儲中.但是,單粒子自旋流在鐵磁體內僅能傳輸幾到十幾納米[9],這完全達不到實際應用的要求.令人興奮的是,最近實驗發現由自旋相同的三重對組成的自旋極化超流可以在強鐵磁體和半金屬(half-metal)中傳播幾百納米[10,11],這為電子自旋在實際中的應用提供了一種有效的方法和途徑.在過去的十年里,人們設計了一系列裝置: 將超導體的零電阻特性與鐵磁體中的自旋極化電流結合在一起,形成可以遠距離傳輸的自旋極化超流.作為一個新的研究領域,它在自旋電子學和量子信息中表現出了非常誘人的應用前景.

超導體與均勻鐵磁體接觸可以在超導/鐵磁界面附近形成鄰近效應(proximity effect)[2]: 當Cooper 對從超導體穿透進入鐵磁體時,鐵磁體內的交換相互作用會使自旋單重Cooper 對(↑↓-↓↑)獲得一個質心動量±Q(Q∝2h/(?vF),其中h為鐵磁交換場,vF為費米速度),從而形成一種自旋單重對和自旋三重對的混合(↑↓)eiQR-(↓↑)e-iQR=(↑↓-↓↑)cos(QR)+i(↑↓+↓↑) sin(QR)[4,7],其中(↑↓+↓↑)表示自旋相反的短程自旋三重對.自旋單重對 (↑↓-↓↑) 在鐵磁層內會隨著質心坐標R振蕩衰減,這種振蕩行為可以引起一系列新穎的效應,如S/F 雙層結構中電子態密度的空間振蕩[12]以及超導轉變溫度Tc隨鐵磁厚度的非單調變化[13].若鐵磁體具有非均勻磁矩,則有可能形成自旋相同的三重對.最具代表性的結構是在S/F 界面附近引入非共線磁矩,由非共線磁矩引起的自旋翻轉(spin-flip)效應能夠將S 內的自旋單重對(↑↓-↓↑)轉化成F 內自旋相同的三重對 (↑↑) (或↓↓)[4,6,7].這種自旋三重對的波函數在空間上各向同性,具有空間坐標交換不變性和自旋交換不變性.因此,其波函數是空間坐標和自旋的偶函數.若要滿足泡利不相容原理,該波函數必須是時間坐標的奇函數,這種新穎的配對方式稱為奇頻自旋三重對(odd frequency spin-triplet pair)[3].這種三重對不會被交換場破壞,能夠在F 層內傳輸很長的距離,數量級可以達到自旋單重Cooper 對在正常金屬內的穿透深度,因此被稱為長程自旋三重對.

另外,兩個超導體被一個鐵磁體分開可以形成一個鐵磁Josephson 結(S/F/S).這是一種非常有應用前景的自旋裝置,其可以通過電子自旋來改變臨界電流.前述的自旋單重Cooper 對波函數的振蕩行為在均勻鐵磁Josephson 結中表現為: 隨著鐵磁長度的變化Josephson 結的基態在0-態(相同的超導位相)和π-態(超導位相差為π)之間轉變.這種0-π 態轉變在實驗中表現為臨界電流隨鐵磁厚度和溫度的增加振蕩衰減[14?16].π-態Josephson 結已經在實際裝置中被用于實現量子計算中的超導量子比特[17].

與之相比,若Josephson 結中的鐵磁體具有非均勻的磁序結構,則鐵磁體內形成的自旋相同的三重對 (↑↑) (或↓↓)能引起長程的Josephson 電流[18?22].很多實驗已經觀測到了上述自旋相同的三重對在鐵磁體內的長程輸運現象[10,23?28].在眾多非均勻鐵磁Josephson 結中,最著名的是Houzet 和Buzdin[21]提出的S/FL-F-FR/S 結構,其中FL和FR界面的磁矩方向與中間的F 層非共線.他們建議通過測量Josephson 結中的臨界電流來證明自旋相同的三重對的存在.然而,他們的研究采用準經典模型求解Usadel 方程.這種準經典方法假定鐵磁交換場遠小于費米能h?EF,并且需要滿足嚴格的條件hτ?1,其中τ 表示電子散射時間.由于鐵磁體內多數電子和少數電子的輸運性質差異較大,準經典方法失去了其有效性,這將導致一些奇妙的量子效應被忽略.另外,很多研究S/F 異質結的實驗都采用強鐵磁體,而準經典近似不能進行充分的定量描述.彌補準經典模型缺陷的一種有效方法是采用微觀方法求解Bogoliubov-de Gennes (BdG)方程.對于非均勻鐵磁Josephson 結,一般很難得出BdG方程的解析解,通常采用精確的數值計算對準經典結果進行修正.

基于上述原因,本文采用純量子的Andreev(安德列夫)能譜法研究一維鐵磁Josephson 結中的電流輸運特性.研究發現,對于短的弱鐵磁S/F/S 結,臨界電流會隨著鐵磁厚度和交換場強度增加振蕩衰減.與之相比,對于具有非共線界面磁矩的S/FL-F-FR/S 結,詳細推導了自旋單重對和自旋三重對在FL-F-FR區域的變換和輸運過程,得出FL和FR界面能夠引起自旋混合(spin-mixing)和自旋翻轉效應.這兩個效應能夠將S 層內的自旋單重對轉化成F 層內自旋相同的三重對.于是,在短鐵磁層內同時存在自旋單重對和自旋相同的三重對.因此,當鐵磁交換場增加時自旋單重對位相的變化能夠引起電流振蕩,而自旋相同的三重對可以使電流維持在一個恒定的值.此外,隨著鐵磁厚度的增加,臨界電流會顯示出兩種振蕩行為的疊加,其中長波振蕩源于自旋單重對位相的改變,短波振蕩源于自旋單重對和自旋相同的三重對穿過FL和FR界面時產生的共振隧穿效應.

2 理論模型

如圖1 所示,本文考慮一個一維S/FL-F-FR/S弱鏈接(weak link).F 層的自旋量子軸沿著z方向,Josephson 電流沿著y方向輸運.取F 層厚度為d,系統的坐標原點位于F 層中心.BCS 平均場有效哈密頓量表示為[29]

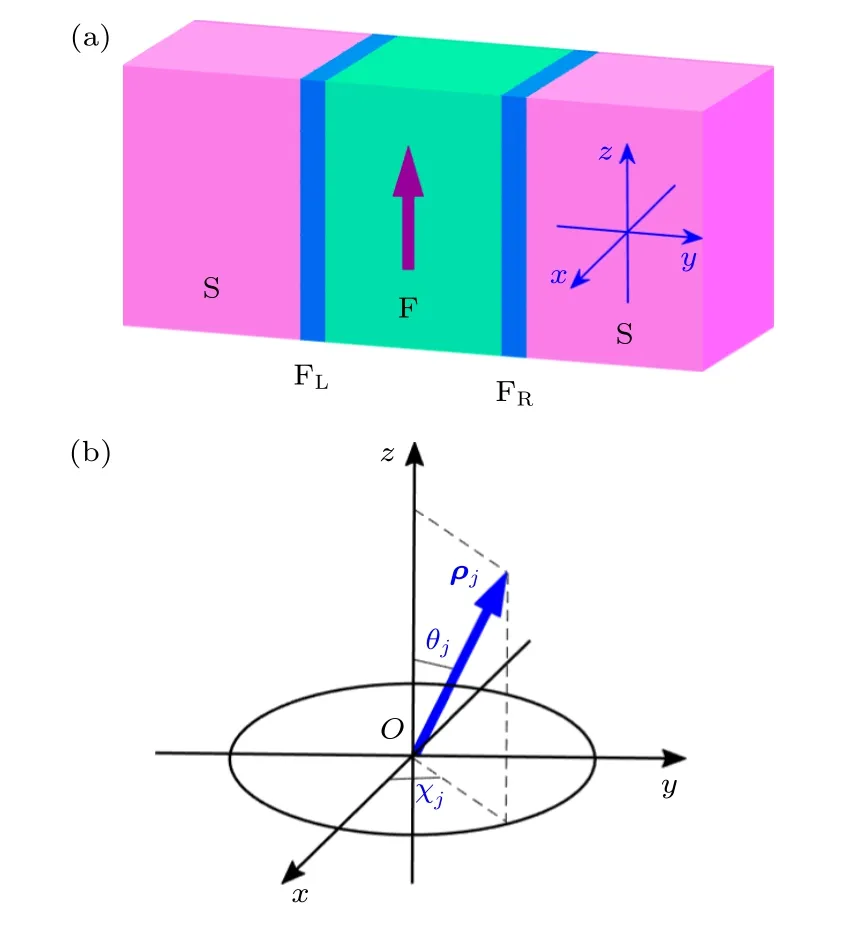
圖1 (a) S/FL-F-FR/S 結的結構示意圖,其中F 內的粗箭頭表示交換場方向,FL 和FR 為具有非共線磁矩的自旋活性界面;(b) Fj 界面處磁矩 ρj 的磁化方向,其中 j=L ,R分別對應左側和右側界面.θj和χj 分別表 示Fj 界面的極化角和方位角Fig.1.(a) Schematic diagram of the S/FL-F-FR/S junction,where thick arrow in F indicates the directions of the exchange field,and the FL and FR are spin-active interfaces with non-collinear magnetic moments;(b) the direction of magnetization ρj at the Fj interface,where j=L andR correspond to the left and right interfaces,respectively.θj and χj denote polar and azimuthal angles of the Fj interface,respectively.

超導能隙在超導電極中為恒定值,在鐵磁區域不存在,可以寫成如下形式:

其中Δ為能隙的幅值,?為兩側超導電極的位相差.該近似在超導長度遠大于鐵磁長度時是合理的.F 層交換 場沿著z方向,可以表示為hz=h(-d/2＜y＜d/2),其中表示沿z方向的單位矢量.這里用一個δ函數ρ(x)=ρLδ(y+d/2)+ρRδ(y-d/2)模擬自旋活性(spin-active)界面,其中ρj(j=L ,R )為Fj界面處的磁化矢量.ρj的各分量通常可以用極化角θj和方位角χj表示為

其中ρj表示界面磁化強度.

下面分別對每個超導電極和鐵磁層求解BdG 方程(4).對于超導能隙中一個給定的能量?,可以得到左側超導電極內的波函數:

利用上述邊界條件可以建立16 個線性方程:

可得出兩個Andreev 束縛態能量EAω(ω=1,2).下面考慮短Josephson 結情況,即F 層長度遠小于超導相干長度ξS.在這種情況下,Josephson 電流主要源于Andreev 束縛態[30,31].在一維弱鏈接中Josephson 電流可由下面的通式計算:

其中Ω是與位相有關的熱力學勢.該熱力學勢源于激發譜,可以用下式計算[32,33]:

其中假定Δ,hz,Pj,θj和χj為處于平衡態的值.這些平衡值依賴于微觀參數,能夠使S/FL-F-FR/S結的自由能最小化[34].在(14)式中僅對所有正的Andreev 能量求和,即取 0＜EAω(?)＜Δ.對于每個給定的?值,數值求解(12)式得到兩個自旋極化的Andreev 能級,然后根據(13)式和(14)式得出Josephson 電流.最終系統中的臨界電流可以由Ic=max?|I(?)|導出.

在數值計算過程中,以超導能隙Δ作為單位能量,并取費米能EF=1000Δ.所有的長度和交換場強度分別以費米波矢kF的倒數和費米能EF為單位進行約化,電流以I0=2eΔ/? 為單位進行約化.文中所有結果皆為溫度T/Δ=0.1 時計算所得.需要說明是,在計算過程中鐵磁體的厚度取值完全滿足短Josephson 結的近 似條件(kFd?1000).如圖1 所示,規定Fj界面處的磁矢量ρj垂直于F 層磁矩,并在x-y平面內轉動,于是θL=θR=π/2 .另外,規定左右兩側FL和FR界面的磁矩偏轉角度差為 δχ=χR-χL.

3 結果與討論

3.1 S/F/S 結中的Josephson 電流

圖2 給出了不含左右界面層(PL=PR=0)時,Josephson 電流隨F 層厚度d和交換場hz的變化特征.圖2(a)顯示了臨界電流Ic變化的三維俯視圖,可以看到電流幅值呈現黃藍相間的條紋.這說明隨著d和hz增加電流幅值周期性振蕩.原本電流應該隨著鐵磁厚度和交換場的增加呈現正負振蕩.正值對應 0 -態,電流方向為正.負值對應π-態,電流方向為負.但是一般在實驗中僅測量電流的幅值變化,不考慮其方向變化.因此,對圖2 中的電流都取了模值以便與實驗對比.為了進一步說明該電流的振蕩行為,在圖2(b)中描繪了不同交換場下臨界電流Ic隨鐵磁厚度d的變化特征.可以看到當F 層為正常金屬(hz/EF=0)時電流緩慢衰減,無振蕩出現.這是由于在正常金屬中自旋向上和自旋向下的能帶簡并所致.當F 層為鐵磁體時( 0＜hz/EF＜1),臨界電流會隨著厚度d的變化而顯示出振蕩行為,其振蕩頻率會隨著hz的增加而增大.若將F 層厚度固定為kFd=60,則交換場取hz/EF=0.05,0.10,0.15 時電流 分別經 歷0.5,1.0,1.5 個振蕩周期.同樣地,若固定鐵磁厚度d連續改變鐵磁交換場hz,臨界電流也會展現出相同的振蕩特征,見圖2(c).

圖2 S/F/S 結中Josephson 電流隨鐵磁特征的變化 (a)臨界電流 Ic 隨鐵磁交換場 hz 和鐵磁厚度d 的變化特征;(b)不同交換場下 Ic 隨d 的變化特征;(c)不同鐵磁厚度時 Ic隨hz 的變化特征; hz/EF=0.15 時的(d)Andreev 能譜 EA(?) 和(e)電流-位相關系 I(?) .在所有圖形中,界面極化強度取PL=PR=0Fig.2.Variation of Josephson current with ferromagnetic characteristics in the S/F/S junction: (a) Critical current Ic versus exchange field hz and ferromagnetic thickness d;(b) dependence of Ic on d for different exchange fields;(c) dependence of Ic onhz for different ferromagnetic thicknesses;(d) Andreev energy spectrum EA(?) and (e) current-phase relation I(?) forhz/EF=0.15 .In all panels,the strengths of interfacial polarization are taken as PL=PR=0 .

另外,為了說明Josephson 電流的0-π 態轉變特征,圖2(d)和圖2(e)中分別給出了kFd=20.8,31.3 和41.6 時的Andreev 能譜EA(?) 和電流-位相關系I(?),這3 個特殊厚度分別對應圖2(b)中的A,B和C三點.由于鐵磁厚度較小,在超導能隙Δ內Andreev 能譜中只包含了兩個能帶.眾所周知,Josephson 電流滿足關系式I(?)=Ic1sin(?)+Ic2sin(2?)+···[1].由于高階電流的幅值非常小,一般情況下只考慮一階電流Ic1和二階電流Ic2的貢獻.當鐵磁厚度為kFd=20.8 時,兩個Andreev能譜曲線幾乎重合,此時Josephson 結處于π-態,即Josephson 電流近似地滿足函數關系:I(?)≈Ic1sin(?+π) .當kFd=31.3 時,Josephson結 處于0-態和π-態轉變的臨界點,此時Andreev能譜分為上下兩個能帶.Josephson 電流的幅值減小,但其隨?的振蕩頻率翻倍.這是由于此時一階電流完全消失(Ic1=0),系統中僅剩二階電流,該電流滿足關系I(?)≈Ic2sin(2?) .若kFd增加到41.6,Josephson 結處于0-態,則電流關系可以表示為I(?)≈Ic1sin(?).此時,兩個Andreev 能帶挨得非常近.這里值得注意的是,在以上kFd變化過程中Andreev 能譜曲線的形狀會發生改變,但其始終關于?/π=1 軸線對稱,見圖2(d).

3.2 S/FL-F-FR/S 結中的Josephson電流

首先討論臨界電流Ic隨交換場強度hz的變化特征.圖3 中當F 層為鐵磁體時( 0＜hz/EF＜1),臨界電流Ic的幅值會隨著交換場hz增加而振蕩.這種振蕩不同于前述的0-π 態轉變引起的振蕩,電流幅值以Ic/I0～0.3 為基準面上下波動,最小幅值不能達到0.當F 層轉變成半金屬時(hz/EF≥1),振蕩特征隨之消失.另外,電流振蕩的峰谷位置與界面磁矩偏轉角度差 δχ有關.當F 層為鐵磁體時,電流的振蕩特征在 δχ=0 ,π 處最明顯,在δχ=π/2 處最弱.電流在 δχ=0和δχ=π 處的振蕩亦不相同.同一交換場下,若電流在 δχ=0 處為峰,則在 δχ=π 處必為谷,反之亦然.當F 層為半金屬時,電流幅值會隨著交換場hz的增加緩慢減小,但卻不隨角度差 δχ變化.

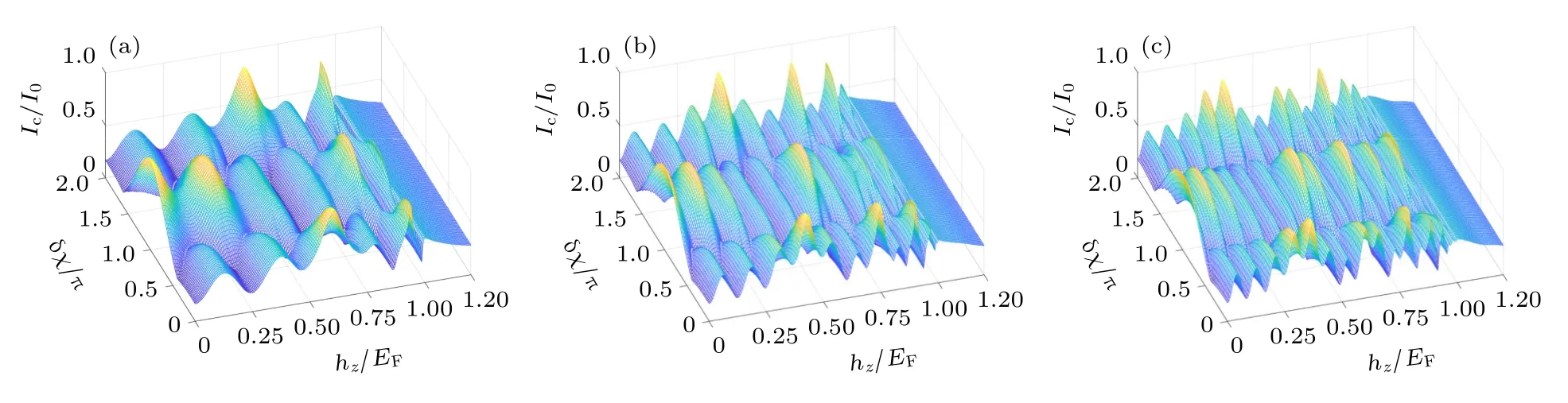
圖3 臨界電流 Ic 隨鐵磁交換場 hz和界面磁矩偏轉角度差 δχ 的變化 特征 (a) kFd=25;(b) kFd=50;(c) kFd=70.在所有圖形中,界面極化強度取PL=PR=1Fig.3.The critical current Ic versus exchange field hz and angle difference of interface magnetization rotation δχ : (a) kFd=25;(b) kFd=50;(c) kFd=70.In all panels,the strengths of interfacial polarization are taken as PL=PR=1 .

需要強調的是,上述臨界電流在一個基準面上上下振蕩是F 層內自旋相同的三重對 (↑↑)z,(↓↓)z和自旋單重對 (↑↓-↓↑)z共同作用的結果.自旋相同的三重對 (↑↑)z和(↓↓)z在F 層內的長程輸運能夠使臨界電流維持在一個基準面上,并且隨著F 層厚度d的增加基準電流的幅值幾乎保持不變.另一方面,臨界電流幅值的上下波動是由自旋單重對 (↑↓-↓↑)z穿過F 層時獲得一個位相Qd引起的(Q∝2hz/?vF),或者說臨界電流的振蕩周期與Qd有關.若d取較小的值,要使臨界電流振蕩一個周期(Qd改變2π 角度),鐵磁交換場hz必須增加較大的值,這樣臨界電流的振蕩波長較大,而振蕩頻率較小.若d取較大的值,則振蕩波長變小,振蕩頻率增大.在圖3(a)—(c)中,分別給出了鐵磁厚度kFd=25,50,75 時臨界電流Ic隨交換場hz的振蕩特征,可以看出隨著d的增加臨界電流的振蕩頻率明顯增大,這與上述物理解釋完全一致.另外,圖3 所示的臨界電流基準值Ic/I0～ 0.3 并非一個普適常數.這是由于基準電流是由F 層內自旋相同的三重對 (↑↑)z和(↓↓)z的數量決定的,而自旋相同的三重對的數量取決于界面FL層和FR層的轉化效率——界面FL層和FR層將超導體內的自旋單重對 (↑↓-↓↑) 轉化成鐵磁體內的自旋相同的三重對 (↑↑)z和(↓↓)z的轉化效率.也就是說,臨界電流的基準值會隨著界面極化強度PL和PR變化.根據后面將要論述的臨界電流隨界面極化強度的變化規律可以粗略估算出臨界電流基準值最大可以達到Imax/I0～0.4 .

下面詳細論述自旋單重對和自旋三重對在S/FL-F-FR/S 結內的轉化和輸運過程,這樣可以更好地解釋上述電流的變化特征.在S 內的自旋單重對 (↑↓-↓↑) 在進入FL區域后受到界面交換場的作用而形成一種自旋單重對和三重對的混合(↑↓-↓↑)θ,χcos(QR)+i(↑↓+↓↑)θ,χsin(QR),其中下標 (θ,χ) 表示自旋單重對和三重對在 (θ,χ) 方向的投影.由于F 層沿著z方向極化,則從FL層到F 層的過程中鐵磁體的極化方向將發生旋轉.自旋單重對從FL層進入F 層具有旋轉不變性[7,35]:

FL層內沿著 (θL,χL) 方向極化的自旋三重對在進入F 層后會進行如下變換[7,35]:

為了使臨界電流達到最大,FL層和FR層的磁矩被限定在x-y平面內旋轉,此時θL=θR=π/2 .于是,上述自旋三重對的變換公式可簡化成:

以上自 旋三重對由 (↑↓+↓↑)θL,χL轉變為 (↑↑)z和(↓↓)z的過程被稱為自旋翻轉效應.緊接著上面的過程,自旋三重對從F 層進入FR層將會經歷如下變換[35]:

將θR=π/2 代入(18a)式和(18b)式,化簡后再代入(17)式可以得到:

若忽略FR區域內自旋相同的三重對和對Josephson 電流的貢獻,并取界面磁矩偏轉角度差 δχ=χR-χL,則自旋三重對通過整個FL-F-FR區域的傳輸過程可以總結為

該傳輸過程說明自旋三重對通過整個鐵磁區域后能夠獲得一個振幅因子 cos(δχ),這將導致臨界電流的幅值隨角度差 δχ改變.從以上結論可以看出,當F 層厚度較小時其內同時存在自旋單重對(↑↓-↓↑)z、自旋相同的三重對 (↑↑)z和(↓↓)z.其中自旋單重對能夠引起一個短程的超流,該超流會隨著鐵磁交換場hz和厚度d的增加而振蕩衰減.與之相比,自旋相同的三重對可以不受鐵磁交換場的影響在F 層內遠距離傳輸,從而引起一個長程的超流.這種長程超流隨著hz和d的增加衰減得較為緩慢,且不會產生振蕩效應.因此,在自旋單重對和自旋相同的三重對的共同作用下,臨界電流會隨著hz和d的增加在一個基準面上起伏振蕩.另外,若固定F 層的厚度和交換場強度,臨界電流會隨著 δχ的改變而顯示出振蕩行為,并在 δχ=0,π 處幅值較大,在 δχ=π/2 ,3π/2 處幅值較小.以上結論與圖3 中的數值計算結果相符.

需要特別指出的是,若F 層由鐵磁體轉變成半金屬,則其費米面處僅有自旋向上的能帶存在,因此只有自旋向上的三重對 (↑↑)z可以在F 層內傳輸,自旋向下的三重對 (↓↓)z被完全禁止.此時,在F 層內自旋單重對 (↑↓-↓↑)z也會被完全抑制,由其引起的振蕩效應隨之消失.此時自旋三重對在鐵磁區域的輸運過程可以描述如下:若忽略FR區域內的自旋相同的三重對和對Josephson 電流的貢獻,則自旋三重對經過整個鐵磁區域后能夠獲得一個位相因子 eiδχ,但不能得到振幅因子.因此,半金屬Josephson 結中的電流滿足關系式I(?)≈-Icsin(?+δχ),其中臨界電流Ic的幅值不會隨 δχ變化.

接下來討論具有非共線磁矩的FL和FR界面引起的共振隧穿效應.如圖4(a)和圖4(b)所示,當F 層為弱鐵磁體(hz/EF=0.1)時,隨著厚度d的增加,臨界電流Ic的幅值顯示出兩種振蕩行為的疊加.第一種振蕩的波長為kFλ1≈60,其波長較長稱為長波振蕩.第二種振蕩的波長kFλ2≈3,該波長非常短,稱為短波振蕩.當交換場增大到hz/EF=0.5 時,長 波振蕩的波長變為kFλ1≈12,而短波振蕩的波長kFλ2保持不變,如圖4(c)和圖4(d)所示.若F 層轉變為半金屬(hz/EF=1.01),隨著厚度d的增加臨界電流的長波振蕩消失,短波振蕩雖未消失但其波動幅度變得非常微弱.此時,臨界電流基本維持在Ic/I0～0.4 的基準面上.在半金屬厚度固定的情況下,臨界電流不再隨角度差δχ變化,見圖4(e)和圖4(f).根據以上臨界電流的變化特征,可以推斷得出長波振蕩是由自旋單重對穿過F 層后獲得一個位相Qd引起的.如引言部分所述,臨界電流以Qd為函數進行振蕩.已知Q∝2hz/(?vF),若hz取較小的值,則Q亦較小,要使臨界電流振蕩一個周期(Qd改變 2π 角度),鐵磁厚度d必須增加較大的值,此時長波振蕩具有較大的波長.與之相反,若hz取較大的值,則長波振蕩的波長變小.由此說明長波振蕩的波長與鐵磁交換場hz成反比.當F 層變為半金屬時,自旋單重對被完全抑制,長波振蕩隨之消失.此時,F 層內僅存自旋相同的三重對 (↑↑)z,其在半金屬內可以遠距離傳輸.因此,臨界電流隨厚度d的增加衰減得非常緩慢,且短波振蕩依然存在.

圖4 臨界電流 Ic 隨鐵磁層厚度d 和界面磁矩偏轉角度差 δχ 的變化特征 (a),(c),(e) 電流變化的側視圖;(b),(d),(f) 電流變化的俯視圖.(a),(b) hz/EF=0.1 ;(c),(d) hz/EF=0.5 ;(e),(f) hz/EF=1.01 .在所有圖形中,界面極化強度取PL=PR=1Fig.4.Variation of the critical current with ferromagnetic thickness d and angle difference of interface magnetization rotation δχ :(a),(c),(e) Side view of current changes;(b),(d),(f) top view of current changes.(a),(b) hz/EF=0.1 ;(c),(d) hz/EF=0.5 ;(e),(f) hz/EF=1.01 .In all panels,the strengths of interfacial polarization are taken as PL=PR=1 .

為了進一步說明以上兩種振蕩的變化規律,圖5(a)給出了 δχ取3 個特殊值時臨界電流Ic隨厚度d的變化.可以看到當 δχ=0 和π 時臨界電流的幅值較大,長波振蕩的波長為kFλ1≈60 .與之相對比,δχ=π/2 時臨界電流的幅值減小,長波振蕩的波長也減小為kFλ1≈30 .對比長波振蕩的輪廓可以看出,當 δχ=0 時臨界電流在kFd=30 附近為峰,而當 δχ=π 時此處的臨界電流變為谷.為分析短波的振蕩特征,圖5(b)和圖5(c)給出了3 個特殊鐵 磁厚度kFd=29.9 ,31.5 ,33.0 的Andreev能譜和電流-位相關系,分別對應圖5(a)中的A,B,C三點,其中A,C點為短 波振蕩的峰值 點,B點為谷值點.可以發現,A,C兩點的Andreev 能譜和電流-位相關系幾乎完全重合.此時,能隙Δ內含有兩條能帶,并且呈對稱結構,而Josephson電流近似滿足關系式I(?)≈Ic1sin(?+π) .B點除了幅值有所減小外,電流-位相關系幾乎保持不變.該特征說明短波振蕩并不是由自旋單重對的位相變化引起的.另外,如圖5(b)中的插圖所示,當kFd=29.9和33.0 時臨界電流隨 δχ的變化特征幾乎完全相同,即隨著 δχ增加臨界電流先減小,并在δχ=0.6π 處降到最小,然后在 0.6π＜δχ＜1.4π 區域處于一個平臺,接著從 δχ=1.4π 處開始增加,并在 δχ=2π 處達到最大.當kFd=31.5 時,臨界電流隨 δχ的變化特征不同于以上兩個厚度,而是在δχ=0.66π 處最小,在 δχ= π 處最大.由此可得出,當kFd=29.9 ,33.0 時,Ic隨δχ同步變化; 而當kFd=31.5時則與之不同.最后,圖5(d)和圖5(e)給出了kFd=29.9,Andreev 能譜和電流-位相關系在不同角度差時的變化特征.可以看到,當 δχ=0,π/2,π 時Andreev 能譜都顯示出關于?/π=1 軸線的對稱結構.這里需要強調的是當 δχ由0 增加到 π/2 時,一階Josephson 電流完全消失,二階電流隨之顯現,并滿足關系式I(?)≈Ic2sin(2?) .當δχ增加到π 時,電流會獲得一個額外的位相π,電流-位相關系變為I(?)≈Ic1sin(?) .

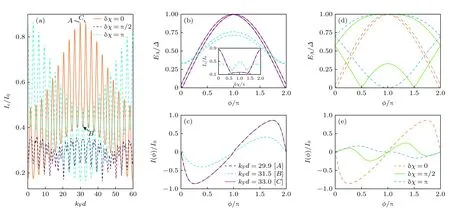
圖5 (a) δχ 取3 個特殊 值時臨界電流 Ic 隨鐵磁 層厚度d 的變化特征;(b),(c) δχ=0時的Andreev能譜 EA(?) 和電流-位相關系 I(?) (圖(b)插圖描述了 Ic隨δχ 的變化);(d),(e) kFd=29.9 時的Andreev 能譜 EA(?) 和電流-位相關系I (?) .在所有圖形中,其他參數為 hz/EF=0.1 和PL=PR=1Fig.5.(a) Variation of the critical current with ferromagnetic thickness d when δχ takes three special values;(b),(c) Andreev energy spectrum EA(?) and current-phase relation I(?) for δχ=0 (the inset in panel (b) illustrates the dependence of Ic on δχ);(d),(e) Andreev energy spectrum EA(?) and current-phase relation I(?) for kFd=29.9 .In all panels,other parameters are hz/EF=0.1 and PL=PR=1 .

根據以上計算結果,可以分析得出短波振蕩是由自旋單重對和自旋相同的三重對的共振隧穿效應引起的.這是因為具有非共線磁矩的界面層除了能夠將超導體內的自旋單重對轉化為鐵磁體內自旋相同的三重對外,還可以起到普通勢壘的作用.根據量子力學的結論[36?38]可知,當粒子以低于勢壘高度的能量E( 0＜E＜V0,V0為勢壘高度)入射到含有雙勢壘的系統中時能夠產生一個共振隧穿效應.該效應表現為: 粒子的透射系數或透射概率會隨著兩勢壘間距的增大而展現出周期性的振蕩峰,透射系數的最大值可以達到1[36].與之類似,超導體內的自旋單重對在穿過FL和FR界面層時也可以產生共振隧穿效應,即Josephson 電流的透射概率隨著兩界面層間距(即中間鐵磁層厚度d)的增加而產生周期性的振蕩峰.需要強調的是,這種周期性振蕩峰的位置只與鐵磁厚度d有關,不會受鐵磁交換場hz的影響.當F 層轉化為半金屬時,F 層內僅存的自旋相同的三重對也能產生共振隧穿效應,但是由其引起的電流共振峰幅值卻非常小.

最后,討論臨界電流Ic隨界面極化強度PL和PR的變化規律.對于弱鐵磁體(hz/EF=0.1),如圖6(a)所示,當界面層不存在時(PL=PR=0)臨界電流最大.隨著極化強度的增加,臨界電流先減小后增大,然后形成一個以PL=PR=0.92 為頂點的凸起.若繼續增加極化強度,臨界電流單調減小.對于中等強度的鐵磁體(hz/EF=0.5),如圖6(b)所示,臨界電流雖然保持與前面相同的變化規律,但其頂點移至PL=PR=1.24,并且凸起的區域有所擴大.造成以上電流變化特征的原因可以解釋如下.具有非共線磁矩的界面在Josephson 結中扮演了兩個重要的角色: 1)在FL和FR界面處存在自旋混合和自旋翻轉效應,該效應可將超導體內的自旋單重對轉變為鐵磁體內自旋相同的三重對;2)FL和FR界面還可以起到普通勢壘的作用,即能夠阻礙超導體內的自旋單重對向鐵磁層的傳播.因此,超導體內的自旋單重對在傳輸進入鐵磁區域時有一部分會被界面層抑制,有一部分化成鐵磁體內自旋相同的三重對.當界面極化強度PL和PR增加時,界面勢壘對自旋單重對的抑制作用增強,這將導致電流幅值減小.與之相反,自旋相同的三重對的轉化效率會隨著PL和PR的增加而增大,于是自旋三重對對電流的貢獻也隨之增大.PL和PR剛開始增加時,前一種效應對電流的抑制作用大于后一種效應對電流的促進作用,最終導致電流幅值有所下降.當PL和PR增大到某個值時,后者對電流的貢獻大于前者,電流幅值將會增大.自旋三重對的轉化效率最高時,電流達到峰值.繼續增加PL和PR的強度,自旋三重對的轉化已經達到飽和,其對電流的貢獻將不再增加,但界面勢壘對電流的抑制作用會持續增加,此時電流幅值將會一直減小.

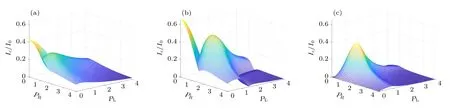
圖6 δχ=0 時不同 鐵磁交 換場下 臨界電流Ic 隨界面 極化強度PL和PR 的變化特征 (a) hz/EF =0.1;(b) hz/EF =0.5;(c) hz/EF =1.01.所有圖形中,F層厚度取kFd=50Fig.6.Variation of the critical current with the strengths of interfacial polarization PL and PR for three different exchange fields in the case of δχ=0 : (a) hz/EF =0.1;(b) hz/EF =0.5;(c) hz/EF =1.01.In all panels,the thickness of the F layer is taken as kFd=50 .

此外,由圖6(c)可以看到,當F 層轉變為半金屬(hz/EF=1.01)時臨界電流的變化規律與前述的鐵磁體情況不同.隨著界面極化強度的增加臨界電流先 增大后減小,在PL=PR=1 處達到最大.臨界電流增加的速度較快,而減小的速度較為緩慢.這是由于在半金屬中自旋單重對被完全禁止,其對電流不會作出任何貢獻.因此,當左右兩側的界面層其中一個或同時不存在時,超導體內的自旋單重對無法轉化成半金屬中自旋相同的三重對,從而導致系統中不能形成Josephson 電流.隨著PL和PR的增加,界面層的轉化率將會提高,電流隨之增大.當界面層的轉化率飽和時電流達到最大.隨后,若繼續增加PL和PR,界面層的抑制作用會使電流減小.需要強調的是,與我們以前的工作相比[39,40],當前的結果中并未顯示出臨界電流隨PL和PR的振蕩效應.這是因為這里將FL和FR界面層簡化成了自旋活性勢壘,其厚度被忽略.通過數值計算證明,若用具有非共線磁矩的實際鐵磁層代替界面勢壘,則臨界電流的振蕩特性將會復現.

4 結論

本文采用純量子的Andreev 能譜法,通過數值求解BdG 方程研究了一維S/FL-F-FR/S 結中Josephson 電流的輸運特性.研究發現,若FL和FR界面不存在,隧穿進入F 層的自旋單重對會獲得一個額外的位相Qd,該位相導致臨界電流隨著F 層的厚度和交換場強度增加而振蕩衰減.若FL和FR界面存在,則非共線的界面磁矩可以扮演兩個重要的角色.首先,FL和FR界面可以引起自旋混合和自轉翻轉效應,該效應可以將超導體內的自旋單重對轉化為F 層內自旋相同的三重對.對于短S/FL-F-FR/S 結,F 層內同時存在自旋單重對和自旋相同的三重對.因此,隨著F 層交換場的增加臨界電流的幅值會在一個基準面上波動.若將鐵磁體替換成半金屬,F 層內的自旋單重對被完全禁止,電流的振蕩行為隨之消失.其次,FL和FR界面還能起到普通勢壘的作用.隨著F 層厚度的增加,臨界電流幅值展現出長波振蕩和短波振蕩的疊加行為,其中長波振蕩是由自旋單重對所得的位相Qd引起的,而短波振蕩是由自旋單重對和自旋相同的三重對經過兩個界面勢壘時產生的共振隧穿效應引起的.以上研究結果為研制超導量子相干器件提供了理論依據,能夠促進超導自旋電子學的發展.