類鋁離子鐘躍遷能級的超精細結構常數和朗德g 因子*

王霞 賈方石 姚科 顏君 李冀光? 吳勇3) 王建國

1) (北京應用物理與計算數學研究所,計算物理重點實驗室,北京 100088)

2) (復旦大學,核物理與離子束應用教育部重點實驗室,上海 200433)

3) (北京大學工學院,應用物理與技術研究中心,北京 100871)

本文利用多組態Dirac-Hartree-Fock 方法計算了類鋁等電子序列從Si+到Kr23+離子基組態3s23p 2P1/2,3/2能級的超精細結構常數和朗德g 因子.通過系統評估電子關聯效應對Si+和Co14+離子中所關心原子參數的影響,尤其是與內殼層電子相關的關聯效應,構建了可靠精確的計算模型,除Si+離子外,超精細結構常數和g 因子的計算誤差分別控制在1%左右和10—5 的量級.此外,進一步分析了超精細結構常數中電子部分矩陣元和g 因子隨原子序數Z 的變化規律,并擬合了這些物理量與Z 的定量依賴關系,利用擬合公式可以快速計算類鋁離子在14 ≤ Z ≤ 54 區間內任意同位素的超精細結構常數和g 因子.

1 引言

高精度的原子光鐘既可以作為時間計量基準,也可以檢驗物理學基本規律或尋找超越標準模型的新物理[1].目前原子光鐘的精度已經達到10—19水平[2,3],但是物理學家仍然在思考如何超越現有的精度極限.高電荷態離子(highly charged ion,HCI)中束縛電子受較強的原子核庫侖相互作用,不易受環境電磁場的干擾,成為下一代原子光鐘的優選對象之一[4—6].理論預言還發現部分HCI 離子鐘躍遷頻率對精細結構常數隨時間的變化比現有原子鐘更加靈敏[7],可以用于尋找超越標準模型的新物理.Yudin 等[8]提出類鋁離子基組態2P1/2→2P3/2磁偶極躍遷可作為鐘躍遷頻率標準的候選之一,該體系的優勢在于簡單的能級結構和極小的電四極偏移.隨后,Yu 和Sahoo[9]采用相對論耦合簇(coupled-cluster method with singles and doubles excitation approximation,CCSD)方法系統計算了類鋁等電子序列從V10+到Cu16+離子3s23p2P1/2,3/2能級的超精細結構常數和g因子及相關HCI 光鐘需要的原子參數,但未考慮與內殼層電子相關的三激發和四激發等高階關聯對相關原子參數的貢獻.超精細結構常數對電子關聯效應非常敏感,原子態波函數的品質很大程度地影響了計算精度.因此,為了給今后HCI 光鐘提供精確可靠的原子參數,有必要分析未被考慮的關聯效應對相關原子參數的影響.

此外,原子超精細結構的實驗測量與超精細結構常數的精密計算相互結合是確定原子核電磁多極矩的有力工具,通過這種方法確定的原子核電磁多極矩獨立于原子核模型,為檢驗原子核結構理論提供了重要依據[10,11].與中性原子相比,HCI 中原子核與核外電子之間的庫侖相互作用占主導,有利于提升原子結構計算精度,獲得更可信的原子核性質.類鋁離子超精細結構常數的高精度計算將為獲取相關核性質提供必不可少的原子參數.

類鋁離子的高精度光譜在天體物理和聚變等離子體領域也有重要的應用[12].例如,類鋁的Fe13+離子2P1/2→2P3/2躍遷是太陽日冕中可見光范圍內的主要譜線之一,并且在其他恒星以及星系星團中也已經觀測到這些譜線[13],利用這些譜線可以確定恒星溫度和密度等狀態參數,為分析恒星形成機制和演化過程提供了理論基礎.朗德g因子和超精細結構常數是分析天體物理中磁場強度以及精確測定恒星元素豐度的重要參數[14—16].高精度的類鋁離子超精細結構常數和g因子將為今后開展相關光譜分析奠定重要的理論基礎.

本文用多組態Dirac-Hartree-Fock (multi-configuration Dirac-Hartree-Fock,MCDHF)方法研究了類鋁等電子序列從Si+到Kr23+離子基組態3s23p2P1/2,3/2能級的超精細結構常數和g因子.通過系統分析電子關聯效應對Si+與Co14+離子計算結果的影響,發現與內殼層2p 軌道相關的電子關聯較為重要,其對超精細結構常數的貢獻最大能達到18%.在此基礎上,考慮了Breit 相互作用和量子電動力學修正,除Si+離子外,超精細結構常數和g因子的計算精度分別達到1%和10—5量級.本文進一步分析了超精細結構常數中電子部分矩陣元和g因子沿類鋁等電子序列的變化規律,并給出了這些物理量與原子序數Z的依賴關系.基于擬合公式計算的超精細結構常數與從頭計算的結果符合得很好,因此可以用于計算類鋁離子在區間14 ≤Z≤ 54 內任意同位素的超精細結構常數和g因子.

2 理論方法

2.1 MCDHF 方法

在MCDHF 理論框架[17]下,原子態波函數(atomic state wavefunction,ASF)Ψ可由具有相同宇稱P和總角動量J及其在z方向分量MJ的組態波函數(configuration state wavefunction,CSF)Φ 線性展開,即

其中,γr和Γ 分別是描述CSF 和ASF 必要的其余量子數,NCSF是組態波函數的個數,cr是組態混合系數.組態波函數是單電子Dirac 軌道波函數構成的Slater 行列式波函數的線性組合.理論上,當組態波函數的個數為無窮多時才能描述真實的原子態波函數,但是在實際計算中只能選擇有限個組態波函數,所以組態波函數的選取方式和數目多少決定了電子關聯效應的考慮程度,直接影響原子態波函數的品質和原子參數的精度.

基于變分原理,利用自洽場(self-consistent field,SCF)方法同時優化軌道波函數和組態混合系數使所研究的原子態能量達到最低,從而獲得一套軌道基組.在獲得單電子軌道基之后,利用相對論組態相互作用(relativistic configuration interaction,RCI)方法可以系統地考慮電子關聯效應.需要注意的是,RCI 計算過程中只會改變組態混合系數,單電子軌道波函數不再發生變化.另外,在RCI中還可以包括Breit 相互作用和量子電動力學(quantum electrodynamics,QED)修正[18].

2.2 超精細結構常數

超精細相互作用是由原子核的電磁多極矩與電子部分的相互作用引起的[19],相應的哈密頓量表示為

其中T(k)和M(k)分別是電子和原子核部分的k階張量算符.k=1 表示磁偶極相互作用,k=2 表示電四極相互作用,文中只包括了這兩項.磁偶極超精細結構常數為

電四極超精細結構常數為

其中I,μ,Q分別代表原子核的核自旋、磁偶極矩、電四極矩.在原子單位下,電子部分的張量算符T(1)和T(2)分別為

其中,i 是虛數單位;α 是精細結構常數;αj是狄拉克矩陣;rj是第j個電子到原子核的距離;l是軌道角動量算符;C(k)是k階球張量算符,它的分量與電子部分球諧函數的關系為

從(3)式和(4)式可以看出,超精細結構常數中電子部分矩陣元Ael=AI/μ和Bel=B/Q與原子核無關,其值完全可以由原子結構的計算確定.而且,在精確確定這些矩陣元的基礎上,可以從實驗上測量的超精細結構中提取相應的核結構參數.

2.3 朗德g 因子

塞曼效應是由原子磁矩和外靜磁場之間的相互作用引起的[20],其哈密頓量可寫為

其中,μB是玻爾磁子,B為磁感應強度,J為電子的總角動量算符,g為朗德g因子.進一步朗德g因子定義為

其角向部分與超精細相互作用電子部分算符(5)式相似.朗德g因子的QED 修正為

其中gs=2.00232.算符ΔN(1)為

其中,β 和Σ 分別是狄拉克矩陣和相對論自旋矩陣.

3 計算模型

本文計算是利用基于MCDHF 方法發展的GRASP2018 程序包[21].在MCDHF 理論框架下,本文采用活動空間方法系統考慮電子關聯效應.根據微擾理論,電子關聯可分為一階關聯和高階關聯.一階關聯用單參考組態單雙激發形成的組態空間描述,又可進一步劃分為價電子之間的關聯(valence-valence,VV)、原子芯電子與價電子之間的關聯(core-valence,CV)以及原子芯電子之間的關聯(core-core,CC).待一階關聯描述充分后,將其組態空間中權重較大的組態加入參考組態基組,用多參考組態基組單雙激發形成的組態空間描述髙階電子關聯效應[10,11,22,23].因為從多參考組態單、雙激發就相當于從單參考組態限制性的三、四激發,實質上優先考慮了較重要的高階電子關聯效應,所以在有限的計算資源下大大提高了計算效率.在本文的計算中,將3s 和3p 軌道看作價軌道,其余1s,2s 和2p 軌道均看作原子芯軌道.

3.1 VV 和CV 關聯

首先,在Dirac-Hartree-Fock (DHF)近似下對參考組態1s22s22p63s23p 的所有占據軌道同時進行優化,并在后續計算中保持不變.隨后考慮VV和CV 關聯,這里的組態空間通過從參考組態中的占據軌道限制性地激發一個或兩個電子到關聯軌道產生的.限制條件為原子芯軌道上至多允許一個電子被激發.表1 給出了SCF 計算過程中具體的計算模型以及Si+和Co14+離子2P1/2→2P3/2激發能隨組態空間擴大的收斂情況.NCSF列數字代表在每個計算模型下組態的數目.通過計算檢驗發現h和i等部分高角動量的關聯軌道對超精細結構常數和g因子的影響分別小于0.1%和10—8,因此沒有將這些軌道加入到活動空間中.如表1 中所列,逐層打開參考組態中占據軌道(active orbitals,AO)的同時,關聯軌道(virtual orbitals,VO)也是逐層添加的,并且每次只對新添加的軌道進行優化,把這部分模型標記為VV+CV-n,n代表活動空間的擴展層數.為了考慮更多電子關聯時能夠達到穩定收斂,活動空間中共包含了10 層關聯軌道,其中前2 層軌道角動量包括s,p,d,f 和g,中間2層軌道角動量包括s,p,d 和f,后6 層軌道角動量包括s,p 和d.相比DHF 計算結果,考慮VV+CV模型后,Si+離子激發能幾乎沒有改變,Co14+離子激發能降低了345 cm—1.

表1 Si+和Co14+離子3s23p 2P1/2,3/2 能級的激發能ΔE (cm—1)隨組態空間擴大的收斂趨勢.DHF 代表單組態計算模型.AO 和VO 分別代表在每個計算模型下允許被激發的占據軌道和新添加的關聯軌道.NCSF 代表相應的組態波函數數目Table 1.Excitation energies ΔE (in cm—1) of 3s23p 2P1/2,3/2 states of Si+ and Co14+ ions as functions of various computational models.DHF stands for the single configuration approximation model.AO and VO represent the occupied orbitals allowed to be replaced and the added virtual orbitals in each computational model,respectively.NCSF represents the corresponding numbers of CSFs.

表2 給出了SCF 計算過程中超精細結構常數電子部分矩陣元Ael和Bel以及朗德g因子隨組態空間擴大的收斂情況.可以看出,Ael和Bel呈現不同程度的振蕩收斂趨勢,g因子最終收斂到10—6.與DHF 計算結果比較,VV+CV 關聯對Si+離子Ael和Bel的貢獻達到15%以上,而對Co14+離子Ael和Bel的貢獻也在7%左右,這表明一階VV 和CV關聯對超精細結構常數計算的重要性.另外,當添加到第9 層和第10 層關聯軌道后,Si+和Co14+離子激發能只有0.001%和0.00035%的差異,但是超精細結構常數卻相差0.1%和0.04%,這表明超精細結構常數受電子關聯的影響更大.

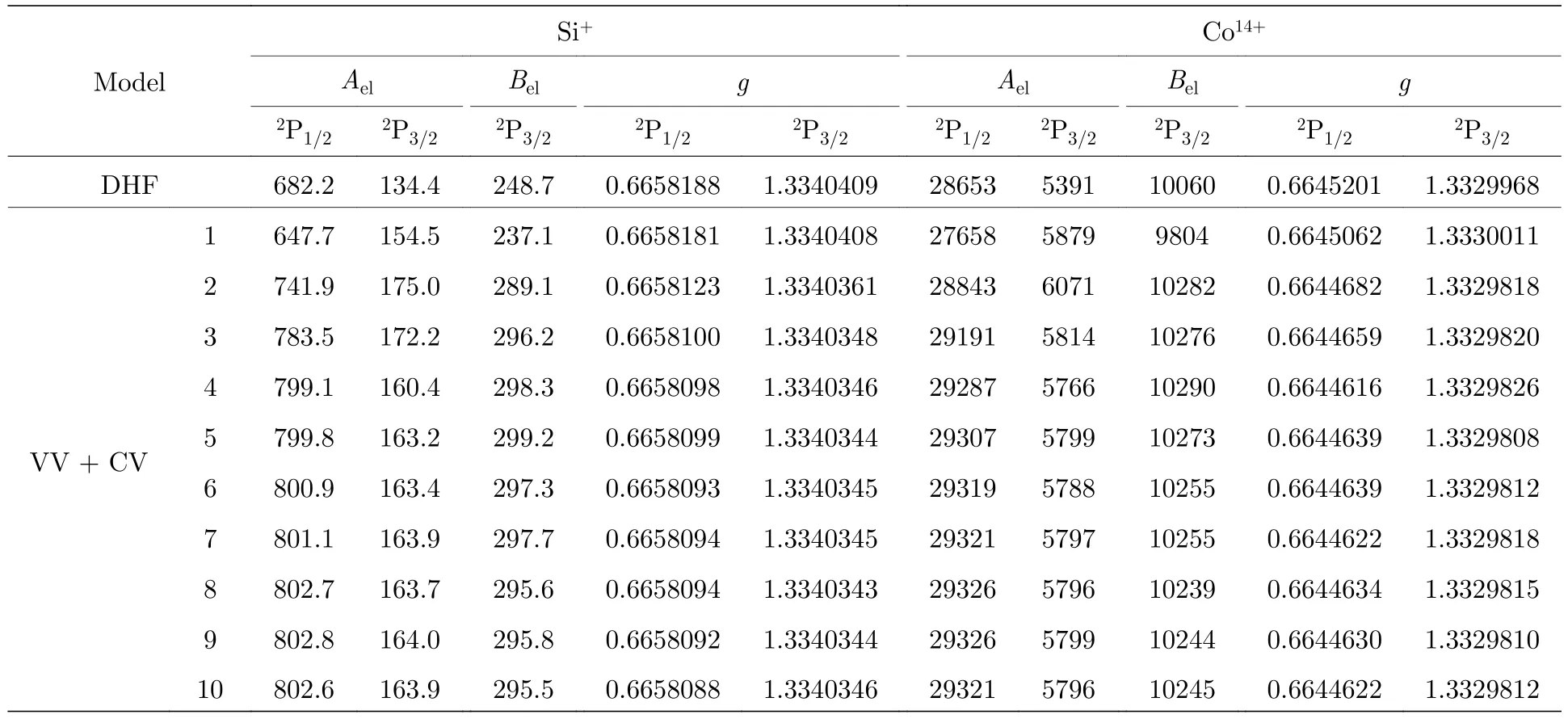
表2 Si+和Co14+離子3s23p 2P1/2,3/2 能級超精細結構常數電子部分矩陣元Ael (MHz/μN)和Bel (MHz/b)以及朗德g 因子隨組態空間擴展的收斂情況.DHF 為單組態近似模型Table 2.Electronic parts of hyperfine structure constants Ael (MHz/μN) and Bel (MHz/b) and Landé g factors of 3s23p 2P1/2,3/2 states in Si+ and Co14+ ions as functions of various computational models.DHF stands for the single configuration approximation model.

3.2 CC 關聯和高階關聯

在充分描述一階VV+CV 關聯的基礎上,采用RCI 方法進一步考慮價殼層軌道的高階關聯以及與內殼層2p 電子相關的CC 和高階關聯,并分析其對計算結果的貢獻.表3 給出了不同計算模型下Si+與Co14+離子3s23p2P1/2,3/2能級的激發能、超精細結構常數電子部分矩陣元Ael和Bel以及朗德g因子.同時為了比較,表3 也列出了CCSD 理論的計算結果[9]和NIST 數據庫的推薦值[24].從表3 中可以看出,電子關聯以及Breit 相互作用和QED 修正對所研究朗德g因子影響較小,因此將系統討論不同計算模型對激發能和超精細結構常數中電子部分矩陣元Ael和Bel的貢獻.

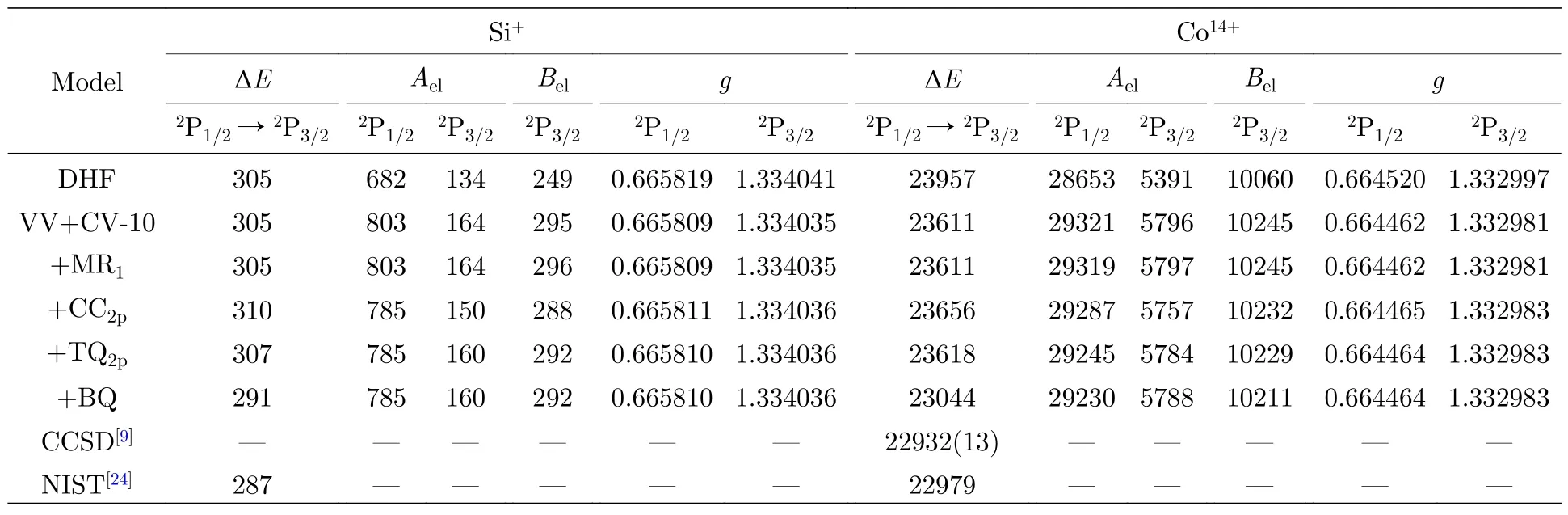
表3 不同計算模型下Si+與Co14+離子3s23p 2P1/2,3/2 能級的激發能ΔE (cm—1)、超精細結構常數電子部分矩陣元Ael(MHz/μN)和Bel (MHz/b)以及朗德g 因子Table 3.Excitation energies ΔE (cm—1),electronic parts of hyperfine structure constants Ael (MHz/μN) and Bel (MHz/b)and Landé g factors of 3s23p 2P1/2,3/2 states in Si+ and Co14+ ions as functions of various computational models.

首先,在VV+CV-10 模型的基礎上,考慮價殼層軌道的高階關聯,即從多參考組態(multireference,MR)占據的3s 和3p 電子單雙激發到關聯軌道所形成的組態空間來描述,標記為MR1.在此模型中,MR 來源于一階VV+CV 關聯原子態波函數中權重大于0.05 的組態,即3p3和3s3p3d;通過監測原子參數隨關聯軌道擴展的收斂趨勢,最終包括5 層關聯軌道.考慮MR1模型后,發現Si+和Co14+離子激發能的變化在1 cm—1以內,該模型對Ael和Bel的貢獻也不超過0.33%.

在MR1模型的基礎上,原子芯中2p 電子的CC 關聯可以通過由單參考組態中的2p 電子雙激發到所有關聯軌道形成的組態來描述,標記為CC2p.研究發現,CC2p模型使Si+和Co14+離子基組態精細結構分裂分別增加了約5 cm—1和45 cm—1(即1.4%和0.2%),對這兩種離子Ael和Bel的貢獻分別為10%和3%左右.

與2p 電子相關的高階關聯效應是計算中的難點,主要原因是內殼層電子關聯效應較弱,在一階關聯原子態波函數中很難挑選出重要的CSFs 作為多參考組態基,因此多參考組態單雙激發的方法并不適合考慮與內殼層電子相關的高階關聯效應.本文采用單參考組態限制性三四激發的方式來考慮這部分電子關聯,該計算模型標記為TQ2p.通過小規模驗證性計算發現f等更高角動量和軌道能較高的關聯軌道以及從參考組態占據的2p 軌道上同時激發出4 個電子對Ael和Bel的影響幾乎可以忽略不計.因此,TQ2p模型共包含了三層軌道角動量為s,p 和d 的關聯軌道;激發方式中允許從2p 軌道和3s,3p 價殼層同時激發1,2,3 和4 個電子,但限制了從2p 軌道的最大激發數到3.TQ2p模型使Si+和Co14+離子基組態精細結構分裂分別減小了約2 和38 cm—1(即0.7%和0.16%),對Ael和Bel的最大貢獻可達6%.CC2p和TQ2p模型不僅存在部分相互抵消,對Si+與Co14+離子超精細結構常數的總貢獻仍有3.7%和0.3%左右,充分說明這兩種電子關聯效應對原子參數計算精度的影響不能被忽略.

從兩個體系不同計算模型的結果比較可以看出,電子關聯效應對原子參數的影響在近中性體系中更顯著,且隨著原子序數的增加而減小.在以上模型產生的組態空間基礎上,對計算結果進行了Breit 相互作用和QED 效應的修正,標記為BQ.這部分修正使Si+與Co14+離子激發能分別降低了16 和574 cm—1(即5.5%和2.5%),對Ael或Bel的貢獻分別為0.06%和0.17%,這說明了Breit 相互作用和QED 效應的貢獻隨原子序數增大而增加.與NIST 數據庫的推薦值[24]和CCSD 方法計算的結果[9]相比,激發能的最大差別不到100 cm—1,由此驗證了當前計算模型的可靠性,為進一步研究類鋁等電子序列超精細結構常數和g因子奠定了一定的基礎.

3.3 計算誤差

在TQ2p模型的基礎上,進一步評估了內殼層2s 和1s 電子的CC 關聯以及與其相關的高階關聯對所研究原子參數的影響.組態空間包括了從單參考組態中2s 和1s 軌道同時激發兩個電子到所有關聯軌道以及限制性三、四激發到部分關聯軌道形成的組態波函數.這里對三、四激發的限制條件為至多1 個或2 個電子從2s 或1s 軌道上被激發.另外,高角動量以及軌道能較高的關聯軌道對所研究的物理量影響很小,因此生成高階關聯波函數時只包含了三層軌道角動量為s,p 和d 的關聯軌道.計算發現描述與1s 和2s 相關的CC 和高階關聯的組態波函數的數量增長了幾倍.但是,除對Si+離子2P3/2能級的磁偶極超精細結構常數的貢獻在3%左右以外,對其他超精細結構常數的影響均小于1%,對朗德g因子的影響被控制在10—5的水平.因此,為了對所研究的等電子系列涉及的所有原子體系使用相同的計算模型并保證計算效率,最終的計算模型中并沒有考慮與內殼層1s 和2s 電子相關的CC 和高階關聯,而將其貢獻作為計算誤差考慮.值得強調的是,如3.2 節所述,電子關聯效應對原子參數的影響隨原子序數增加而減小,結果中所給誤差是基于等電子系列中近中性離子的評估給出,因此對于離化度較高的體系此誤差應比實際誤差大.

4 結果與討論

4.1 Ael,Bel 和g 因子

表4 列出了利用BQ 模型計算的類鋁等電子序列從Si+到Kr23+離子基組態3s23p2P1/2,3/2能級的超精細結構常數電子部分矩陣元Ael,Bel和朗德g因子以及相應的計算誤差.為了更直觀地反映出這些物理量隨原子序數Z的變化規律,進一步在圖1 中展示了計算結果,如散點所示.從圖1 可以看出,超精細結構常數電子部分矩陣元Ael和Bel隨原子序數的增加而增大,g因子隨原子序數的增加而減小.從(5)式和(6)式可以看出,磁偶極和電四極超精細相互作用分別與原子態波函數徑向半徑的平方和三次方成反比,而高離化態離子的波函數徑向半徑近似與原子序數成反比,從中可以定性地解釋超精細結構常數電子部分矩陣元與Z的依賴關系.對于朗德g因子,在非相對論近似下可以通過g=1+[J(J+1)—L(L+1)+S(S+1)]/[2J(J+1)]解析得到,給定角動量量子數其值應與原子序數無關,而圖1 中g因子隨原子序數的變化呈現Z2的依賴關系,可以推斷此變化規律是由相對論效應導致的.

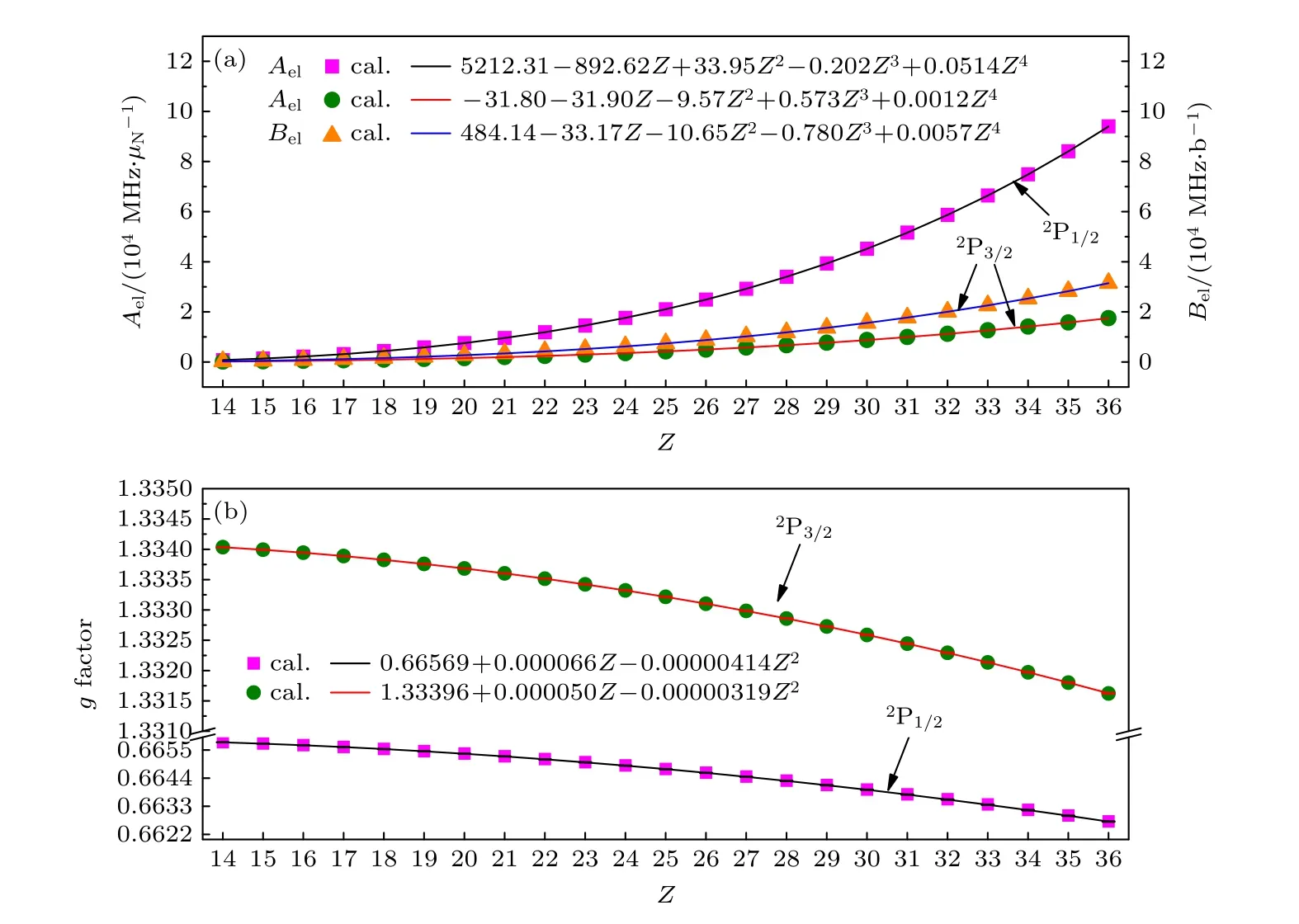
圖1 類鋁等電子序列3s23p 2P1/2,3/2 能級的(a)超精細結構常數電子部分矩陣元Ael 和Bel 以及(b)朗德g 因子隨原子序數Z 的變化關系.圖中實線表示由擬合公式得出的結果,散點表示用MCDHF 方法從頭計算的結果Fig.1.(a) Electronic parts of hyperfine structure constants and (b) Landé g factors of 3s23p 2P1/2,3/2 states of Al-like isoelectronic sequence ions as functions of atomic number.The solid line represents these results obtained by from numerical fitting formula,and the discrete point represents these results obtained by our ab initio calculation using MCDHF method.

表4 類鋁等電子序列3s23p 2P1/2,3/2 能級的超精細結構常數電子部分矩陣元Ael (MHz/μN),Bel (MHz/b)和朗德g 因子.括號內的數字表示計算結果相應的不確定度Table 4.Electronic parts of hyperfine structure constants Ael (MHz/μN) and Bel (MHz/b) and Landé g factors of 3s23p 2P1/2,3/2 states of Al-like isoelectronic sequence ions.Numbers in parentheses represent the computational errors.

進一步,利用多項式擬合了超精細結構常數電子部分矩陣元和g因子與原子序數Z的定量依賴關系,具體表達式列于圖1 中.如圖1 中實線所示,利用擬合公式計算的Ael,Bel和g因子與從頭計算的結果符合得很好,相對偏差小于2%;從頭計算的g因子與擬合結果的相對偏差小于10—5.因此,可以利用擬合結果計算此等電子序列區間內任意同位素的超精細結構常數和g因子.同時這些擬合函數可以進一步推廣到其他類鋁離子,經過理論計算發現,當原子序數Z＜ 54 時,從頭計算和擬合函數結果的相對偏差小于2%,因而該擬合表達式仍然適用,并且對于2P3/2能級的Ael和Bel該擬合表達式還可以推廣到更高Z的離子體系.

4.2 A,B 和g 因子

根據穩定同位素的I,μ[25]和Q[26]以及表4 中給出的超精細結構常數電子部分矩陣元Ael和Bel,可以確定類鋁等電子序列3s23p2P1/2,3/2能級的磁偶極超精細結構常數A和電四極超精細結構常數B.表5 給出了7 種已建議的下一代HCI 光鐘的類鋁離子g因子以及穩定同位素的超精細結構常數A和B及相應的計算誤差.由表5 可知,除59Co14+離子外,本文計算的A值與CCSD 方法計算的結果[9]差別均小于0.5%,而59Co14+離子兩種方法計算的結果相差7 倍以上,原因主要是文獻[9]中引用的原子核磁偶極矩有誤.兩種方法計算的B值差別較大,尤其是對于51V10+,59Co14+離子和55Mn12+,57Fe13+離子,差別分別達到了16%和30%.導致這些差別的原因主要是兩種方法采用了不同的原子核電四極矩推薦值[25,26],而電子部分矩陣元計算引起的差別不到0.25%.因此,通過實驗測量B值,再結合本文計算的Bel,可以重新確定較為可靠的核四極矩Q.本文計算的g因子與CCSD 計算結果的差別在小數點后第四位或第五位.

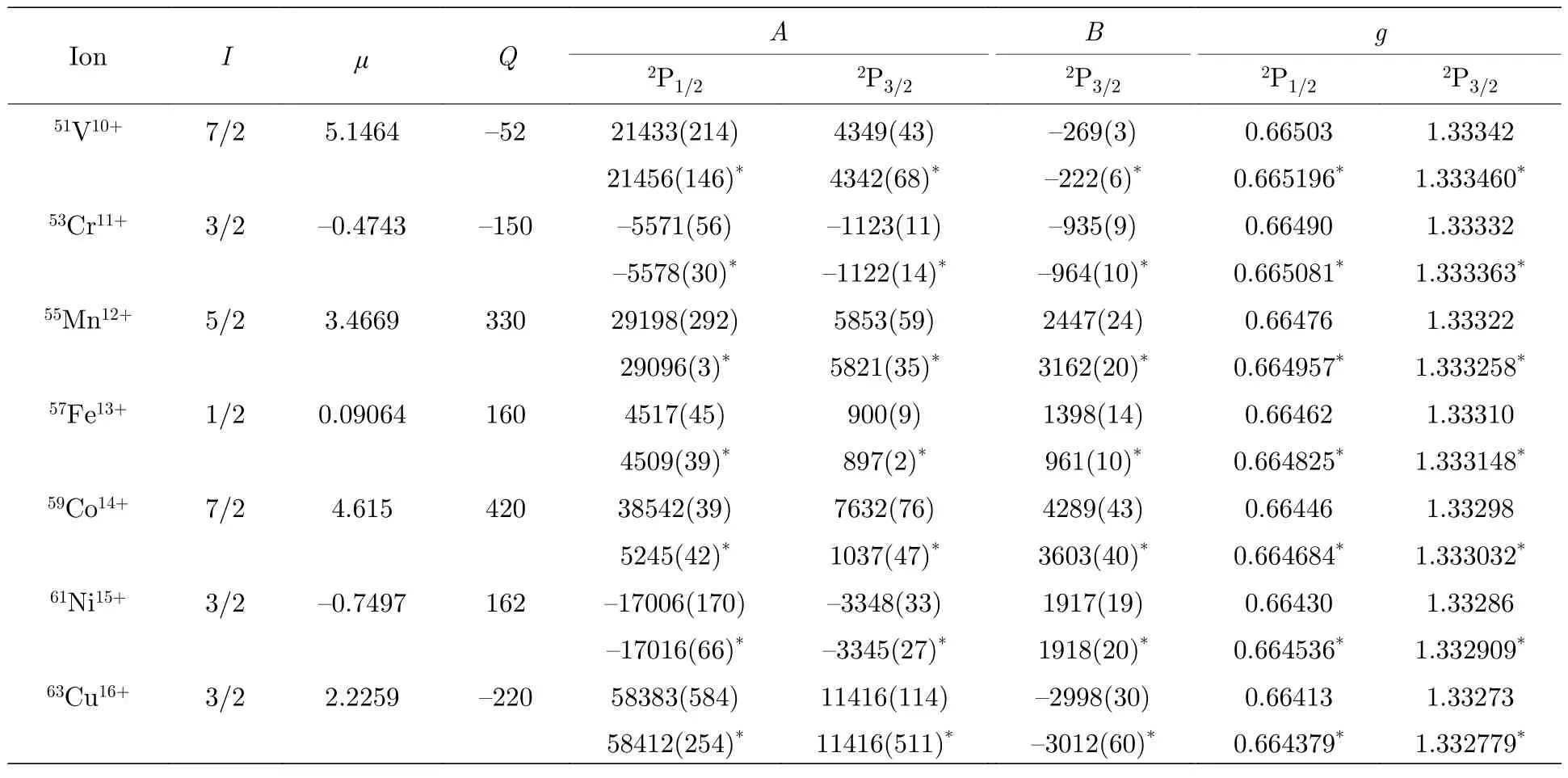
表5 類鋁等電子序列3s23p 2P1/2,3/2 能級的超精細結構常數A,B (MHz)和朗德g 因子.所有核參數μ (μN)和Q (mb)均來自于文獻[25,26].星號表示用CCSD 方法計算的結果[9].括號內的數字表示計算結果相應的不確定度Table 5.Hyperfine structure constants and g factors of 3s23p 2P1/2,3/2 states of Al-like isoelectronic sequence ions.Nuclear parameters μ (μN) and Q (mb) are taken from Ref.[25,26].Asterisk represents these results calculated by CCSD method[9].Numbers in parentheses represent the computational uncertainties.

5 結論

本文采用MCDHF 方法,研究了類鋁等電子序列從Si+到Kr23+離子基組態3s23p2P1/2,3/2能級的超精細結構常數和朗德g因子.通過系統分析了不同類型電子關聯效應對Si+與Co14+離子計算結果的影響,構建了可靠精確的計算模型,除Si+離子外,本文計算的超精細結構常數和g因子的精度分別高于1%和10—5水平.進一步,討論了超精細結構常數和g因子隨原子序數的變化規律,并給出了準確的擬合公式,這些擬合函數也可以進一步推廣到原子序數小于54 的類鋁離子.本文的計算結果為天體物理和原子鐘等研究領域提供了可靠的原子參數.