光電效應的伏安特性曲線
楊 祺,金惠吉,陳海濤,楊厚發,施夢麗,鄭永剛
(1.云南師范大學 物理與電子信息學院,云南 昆明 650092;2.昆明市第八中學,云南 昆明 650032)
當1束光照射到金屬或半導體上時,由于光與載流子之間的相互作用,金屬或半導體的電導率會發生顯著變化,包括光電效應(光子與金屬中的束縛電子相互作用,導致電子脫離金屬晶體,然后躍遷到自由態電子)、光導效應、光伏效應等[1]. 1887年赫茲發現光電效應,1905年愛因斯坦提出的光量子假說成功解釋了光電效應[2]. 在光電效應實驗中,利用光電效應實驗研究儀可以得到光電管中的光電效應伏安特性曲線. 光電效應伏安特性曲線顯示隨著極板加速電壓的增大,光電流趨于飽和[3]. 本文對電子的運動過程進行理論分析,數值計算光電流的伏安特性曲線與實驗數據擬合得到結果較為符合.
1 光電相互作用和光電流
光和電子相互作用的哈密頓量為[4-6]
(1)
其中,Z為原子序數,Aij為不同電子之間的相互作用系數,E為外電場強度,D為量子電偶極矩算符.在光子的作用下,電子從束縛態|i〉躍遷到自由態|k〉,在脫離束縛影響后,對外形成光電流.電子在脫離金屬受光面時,躍遷到自由態的概率時間變化率的方向分布為[4,7]
(2)
(3)
其中,
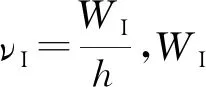
當νR→0時,光電子的分布函數穩定后(t→∞)趨于常量;對于νR≠0,電子空間分布概率隨時間變化存在振蕩行為[4].
由于電子需要脫離表面勢壘的束縛,根據費米統計規律,可以得到出射電流密度為[8]
(4)
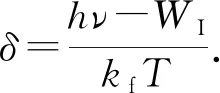
2 光電流的計算
2.1 電子陽極分布函數
電子脫離陰極以后,假設電子的運動分成3部分:電子受光子作用,脫離金屬束縛;電子在真空中受加速電場的作用,到達光電管的接收極板上;到達極板上的電子透射進入電極內部,與接收材料的導帶電子發生相互作用形成電流. 當電子從束縛態變成自由態時(即脫離電極后電子在真空中的運動,對應圖1中的AK段的運動),其電荷密度和電流密度可以按照出現的概率來定義;由于脫離束縛態的自由電子在真空中的運動可以用粒子軌跡來描述,因此采用非量子的近似方法描述電子的運動情況. 當電子到達接收極板后,由于受到極板的原子和電子的影響,近似等效為有限勢壘,電荷按照一定比例透射入材料.
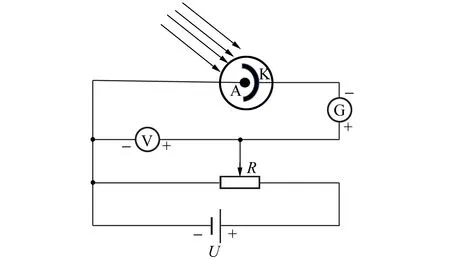
圖1 光電效應實驗儀器電路(AK段為光電管,接受光的照射,其余為外電路,為電子提供加速電壓)
電子因為光電效應的影響而脫離極板K后,在加速電場的作用下沿拋物線運動,初始時的速度v0由愛因斯坦光電效應方程決定[2]:
(5)
其中,WI一般與溫度、材料的費米能級相關,νL為光頻率,me為電子的靜止質量.脫離金屬板后,電子在光電管的板A和板B間的真空中運動,初速度和兩板法線方向(定義為z軸方向)的夾角為θ(稱為方向角),則按照電子運動方程有
(6)
r=v0tsinθ,
(7)
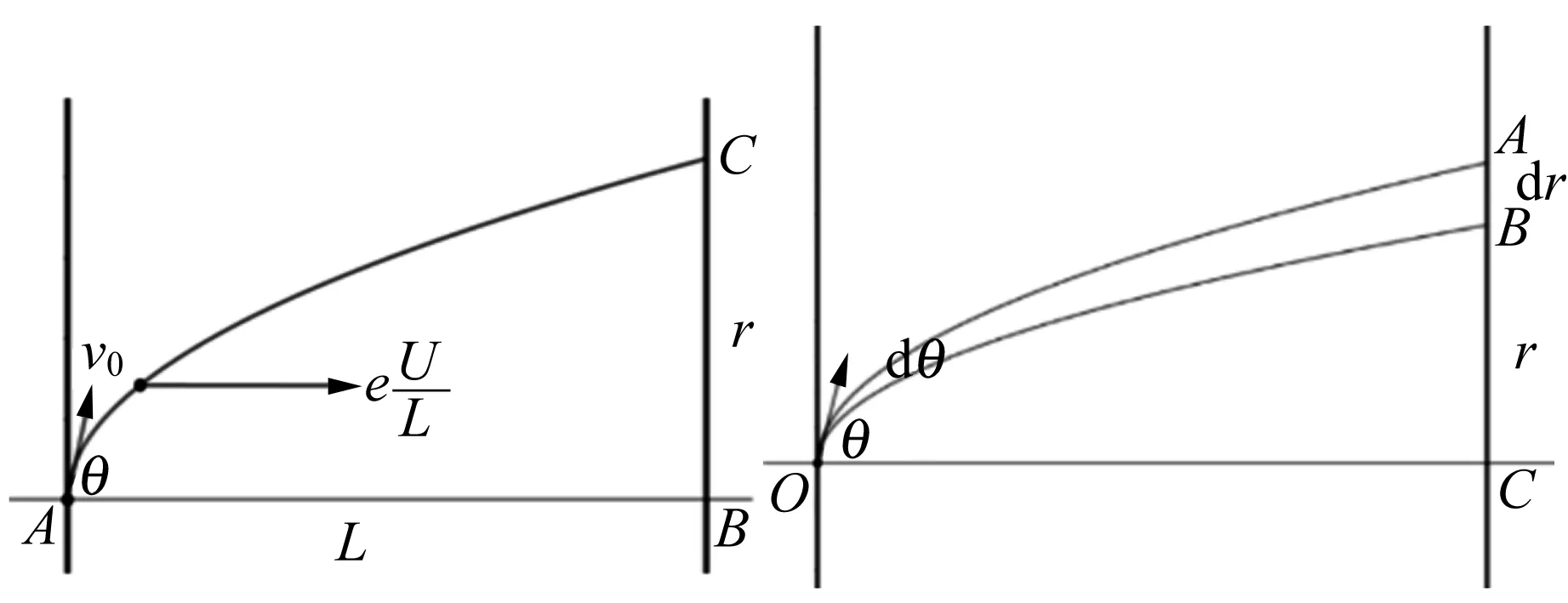
其中,r為接收板法線垂直方向上的運動距離,圖2(a)所示的BC段;L為光電管發射板和接收板之間的間距,如圖2(a)所示的AB段.聯立式(6)和式(7)消去t,得到
(8)
(a) (b)
(9)
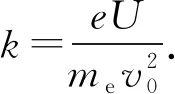
(10)
當k<0時,由于cos2θ+2k>0,所以
(11)
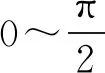
(12)
(13)
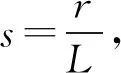
(14)
其中
(15)
由式(11)可以得到,當初始速度v0和z軸的方向角θ變化時,導致接收屏上的電子分布改變.自由態光電子在光電管中被加速電場加速的運動軌跡如圖2所示.假定受光板A與接收板B之間為真空,在加速電場的作用下,電子的軌跡為拋物線.圖2(a)和(c)為電子沿方向角θ的運動軌跡,由于初始方向為沿繞z軸的任意方向φ(方位角),因此電子的運動軌跡為旋轉拋物面.圖2(b)和(d)為從原點處逃逸的電子在加速電場的作用下,方向角為θ和θ+dθ的運動軌跡及軌跡沿不同方向角形成的旋轉拋物面.因為電場的影響,加速后的電子改變了運動狀態分布,在接收板B上的分布函數與自由態時的分布有所不同.
從光電管受光板A[坐標為(x′,y′,0)]逃逸出的電子沿空間分布在立體角dΩ的概率為
(16)
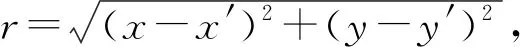
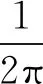
(17)
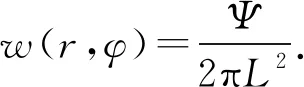
由于A板與B板平行,所以取相同的空間方位角,利用極坐標面積元變換得到
dP=w(r,φ)rdrdφ=w(x-x′,y-y′)dxdy,
(18)
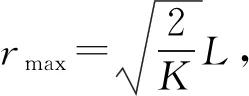
(19)
至此,通過經典理論給出了電子沿空間運動的概率分布函數,通過計算機繪制得到分布函數如圖3所示.
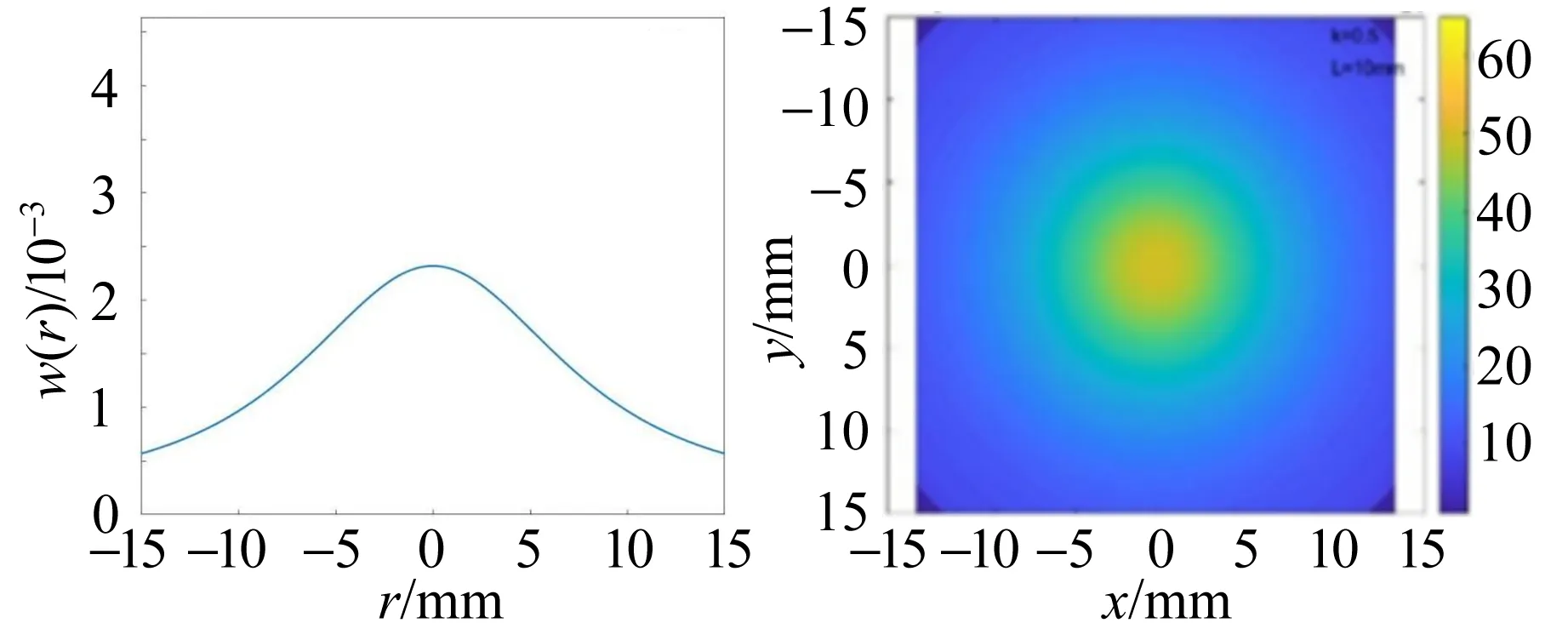
(a)L=10 mm,k=0.5
2.2 陽極電流
電子從板A脫離形成自由態電子的概率分布滿足式(2),因此在板A上點(x′,y′,0)附近單位時間內逃逸的電子數正比于光電子從束縛態到自由態躍遷的概率
(20)
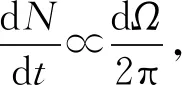
(21)
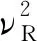
(22)
所以有
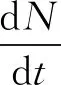
(23)
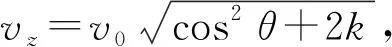
(24)
所以接收板B點(x,y,L)處的電流密度矢量為
(25)
其中Σ′為對板A受光面的積分域.
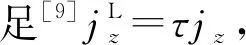
(26)
當w→δ(x-x′,y-y′),得到Ic=Imax=eIτM,所以有
(27)
下面利用式(27)數值計算光電流,其中材料參量M和τ、光電管大小參量未知.可以利用優化算法,選擇合適的參量擬合實驗數據.
3 數值計算和實驗數據擬合
圖4所示的實驗儀器用于測量普朗克常量[10].接通電源,光電管接收到不同光闌濾過的光,在光電管上形成電流,從而測量得到光電效應實驗的伏安特性曲線.由于入射光強和光闌孔徑的平方成正比,因此可以利用該實驗裝置測量光電伏安特性曲線在不同光強下的性質.也可以用來得到材料的功函數[11],這樣材料的功函數可以直接代入式(27).

圖4 LB-PH3A光電效應實驗儀
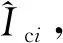
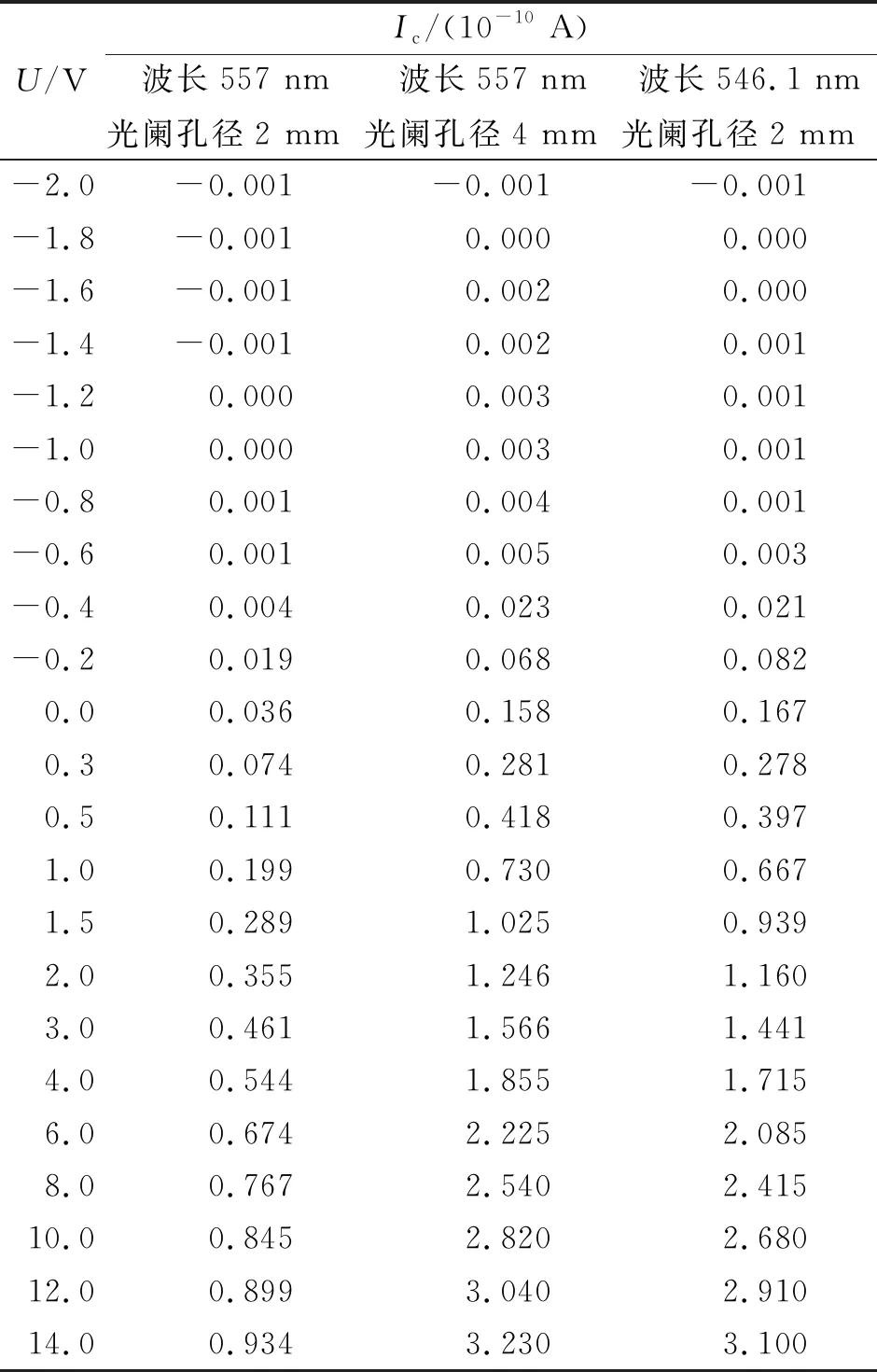
表1 伏安特性曲線的實驗數據
(28)
利用Matlab遺傳算法工具箱,調節未知參量Imax,L和積分區域面積(A1,A2),使d0最小[13].如圖5所示,調整模型參量可得到較好的擬合數據. 3次擬合R2=0.989 6,0.990 5,0.990 3. 這里用到了儀器材料的功函數,對于不同的材料只需選擇合適的功函數就可很好地擬合截止電壓,因此本文的工作具有普遍性. 由于積分步長無法自適應,大于16 V的數值計算結果,需要改變數值算法來完成.
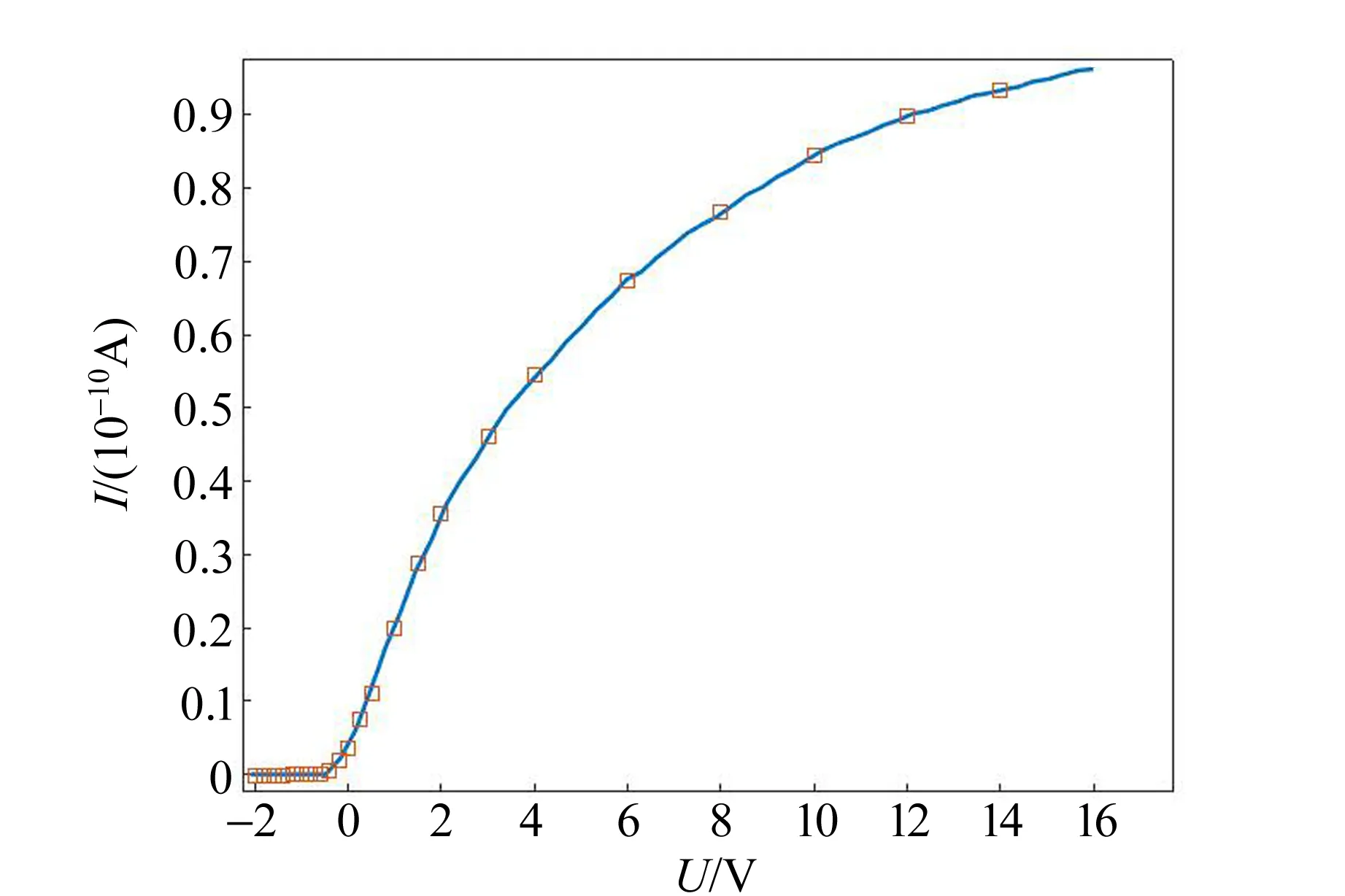
(a)波長557 nm、光闌孔徑2 mm
4 結束語
本文考慮了光電效應的光電流產生過程,通過計算電子在陽極的分布函數,得到了光電流的解析表達式. 利用優化算法(遺傳算法)調節光電流解析表達式中的未知參量獲得光電流值,并將數值計算結果與光電流伏安特性曲線實驗數據進行比較,結果表明:數值計算結果與實驗測量結果一致. 本文為數值計算光電效應伏安特性曲線提供了理論方案,也為開發相關實驗儀器和教學儀器提供了計算模型. 光電效應伏安特性曲線和溫度之間的關系以及材料參量的具體計算方法,將在后續的工作中進行研究.

