運用對稱雙扭擺實驗學習耦合振動規律
徐 楠,鄭星航,周瀅瑤,王才林,張 歡,王克東
(南方科技大學 物理系,廣東 深圳 518055)
耦合振動是理論力學課程中的經典內容[1-2],它建立了簡正模和簡正頻率等基本概念,是分析復雜系統振動問題的重要工具. 長期以來,教材多以彈簧振子[3]為背景講解耦合振動的理論知識,實驗中通常在氣墊導軌上[4]展示彈簧振子的耦合振動特征. 為了拓展學生的視野,文獻[5]基于力學相似性原理[1],類比固定端/彈簧/質塊/彈簧/質塊系統設計了非對稱雙扭擺實驗,以剛體轉動為背景介紹了耦合振動的時間演化圖像、頻譜特征和測量方法,為耦合振動的實驗教學提供了新思路. 由于非對稱雙扭擺裝置在結構上缺乏對稱性,難以展現對稱簡正模、反對稱簡正模和拍等經典現象. 為豐富雙扭擺實驗,類比固定端/彈簧/質塊/彈簧/質塊/彈簧/固定端系統,本文設計了對稱雙扭擺實驗,增加對稱簡正模、反對稱簡正模和拍的調節與觀測. 教學實踐表明:該實驗有助于學生直觀地學習耦合振動的基本規律,掌握通過控制初始條件調節系統振動模式的方法.
1 實驗裝置
對稱雙扭擺裝置主要由支架、鋼絲、轉盤、制動器和手機等5部分構成,如圖1所示.

圖1 對稱雙扭擺裝置圖
支架的頂部和底部裝有緊固夾具,可以懸掛鋼絲. 2個轉盤被緊固于鋼絲的不同位置,將鋼絲分為上、中、下3段. 2個轉盤的形狀相同,上下2段鋼絲的尺寸也相同,形成了對稱結構. 轉盤的直徑為120.00 mm,轉動慣量為0.311 g·m2(含緊固夾具). 上下2段鋼絲的扭轉系數均為K,中段鋼絲的扭轉系數為k.由于扭轉系數依賴于鋼絲的幾何尺寸,因而可以通過鋼絲的直徑和長度調節扭轉系數[5]. 轉盤的釋放和停止受制動器控制. 在斷電狀態下,制動器夾持轉盤使其保持靜止;通電后,制動器釋放轉盤,轉盤可以自由轉動. 轉盤上貼有輕薄紙片,該紙片上印有度盤和標記點,度盤用于設置轉盤的初始轉角,標記點用于追蹤轉盤的轉角. 2部手機分別置于上下轉盤的上方,錄制相應標記點的轉動視頻,錄像幀率為30 s-1.
2 實驗原理
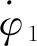
(1)
(2)
其中,I為轉盤的轉動慣量.在實驗中,可通過改變鋼絲的直徑和長度調節K和k[5].將式(1)~(2)代入拉格朗日方程[1]
L=T-V,
(3)
(4)
可得兩轉盤的轉動方程為
(5)
(6)
轉動方程等號右側表示鋼絲施加在轉盤上的回復力矩,其同時依賴于兩轉盤的轉角,可見兩轉盤的轉動存在耦合.另外,式(5)~(6)同一維雙彈簧振子的運動方程具有力學相似性[1]:前者的轉角、角加速度和轉動慣量分別對應于后者的位移、加速度和質量.
為了求解式(5)~(6),不妨假設兩轉盤按相同的角頻率ω轉動,即
φ1=q1sin (ωt),
(7)
φ2=q2sin (ωt),
(8)
其中,q1和q2分別為上下兩轉盤的轉角隨時間演化的幅度.將式(7)~(8)分別代入式(5)~(6),并整理可得本征方程為
(9)
式(9)的非平庸解對應于
(10)
由此可得對稱雙扭擺裝置的簡正頻率為
(11)
(12)
將簡正頻率ωɑ代入式(9)并歸一化,可得
(13)
可見,當兩轉盤均以角頻率ωα轉動時,幅度和方向均相同,故不引起中段鋼絲的扭轉形變,兩轉盤實則為脫耦合.該轉動形式稱為對稱簡正模,ωα稱為對稱簡正頻率.
同理,將角頻率ωβ代入式(9)并歸一化,可得
(14)
即當兩轉盤以角頻率ωβ轉動時,幅度相同但方向相反.該轉動形式稱為反對稱簡正模,ωβ稱為反對稱簡正頻率.
由式(11)~(12)可知,對稱簡正頻率低于反對稱簡正頻率,前者僅依賴于K,而后者還依賴于k.一般情況下,轉盤的轉動是2種簡正模的線性疊加,即
(15)
其中,A和B為疊加系數.
在實驗中,可以通過控制兩轉盤的初始轉角調節耦合轉動形式.令初始時刻φ1和φ2的值分別為φ10和φ20,代入式(15)并整理,可得
(16)
(17)
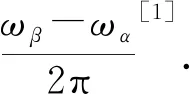
3 實驗方法
實驗操作如下:
1)平穩放置支架,依次懸掛鋼絲和轉盤;
2)根據轉盤位置安裝制動器,將轉盤轉至設定轉角后夾緊;
3)根據標記點位置放置手機;
4)打開手機錄像功能,開啟制動器同時釋放轉盤,拍攝兩轉盤上標記點的轉動視頻,然后依次關閉錄像和制動器;
5)導出兩轉盤上標記點的轉動視頻,運用Tracker提取標記點坐標的時間演化數據.
學習耦合轉動規律的基礎在于分析轉盤轉角的時間演化數據.因此,在數據預處理部分,需要使用反正切函數將標記點的時間演化數據轉化為轉盤轉角的時間演化數據.
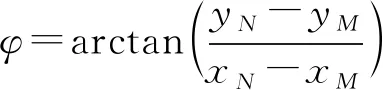
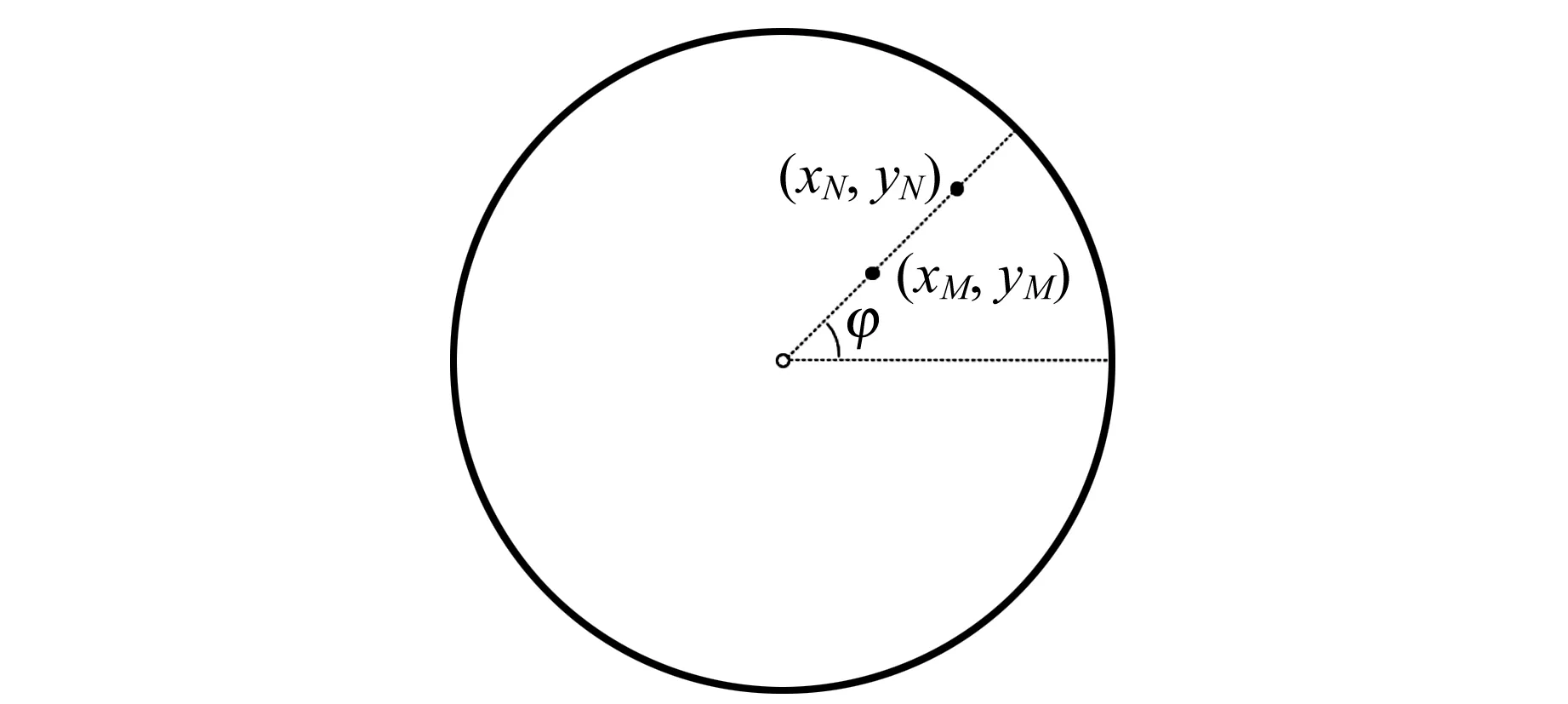
圖2 轉盤上標記點示意圖
4 實驗結果及分析
共使用6種不同尺寸的鋼絲,并運用文獻[6]中的方法測量扭轉系數,結果見表1.其中,扭轉系數K=0.291 9 mN·m的鋼絲充當對稱雙扭擺裝置的上下段鋼絲,其余的鋼絲則先后充當中段鋼絲.按照實驗操作步驟得到不同中段鋼絲的扭轉系數k條件下的上轉盤轉角φ1的時間演化數據,結果如圖3所示.從圖3可以看出,由于兩轉盤之間存在耦合,φ1隨時間t的演化均較為復雜,已經明顯偏離單扭擺的簡諧轉動特征[5].另外,在k較小時,φ1的時間演化具有明顯的拍特征,見圖3(a);但隨k增加,拍特征逐漸消失,見圖3(b)~(e).
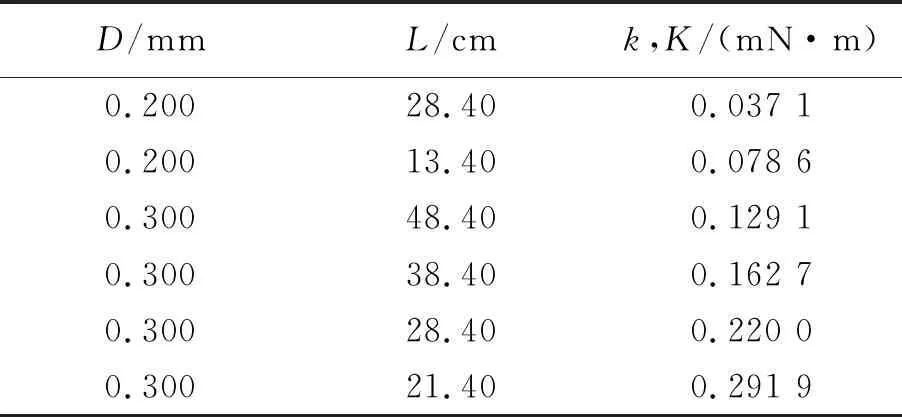
表1 不同尺寸鋼絲的扭轉系數
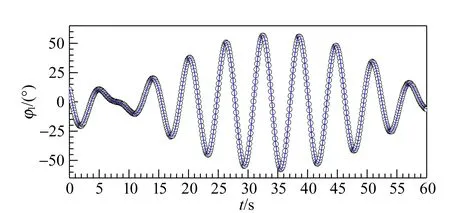
(a)k=0.037 1 mN·m
運用式(15)對圖3中數據進行雙正弦函數擬合,實驗數據和擬合曲線符合良好,說明轉盤轉動包含2種簡正模成分,符合實驗原理預期.為了檢驗角頻率擬合結果的準確性,將K,k和I的值代入式(11)~(12),計算得到對稱簡正頻率ωα和反對稱簡正頻率ωβ,結果如表2所示.從表2可以看出,實驗擬合結果和理論值的相對偏差均低于0.5%.隨k增加,ωα基本不變,而ωβ上升,這是由于當兩轉盤以角頻率ωα做簡諧轉動時,中段鋼絲的彈性勢能維持恒定,故k不影響ωα,如式(11)所示.
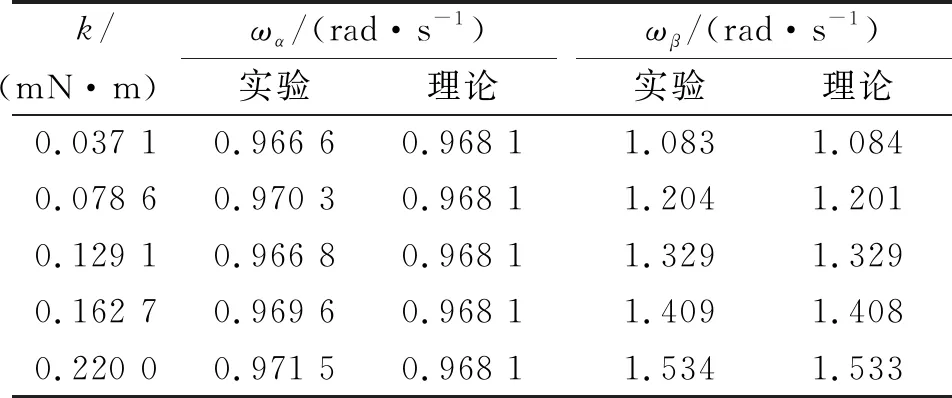
表2 圖3中簡正頻率實驗的擬合值和理論值
圖4直觀地展現了簡正頻率ω隨k的變化關系.由圖4可以看出,簡正頻率分布于2個不同的分支.隨k增加,2種簡正頻率的差距逐漸變大,這也給出了圖3(a)~(e)中拍現象逐漸消失的原因.
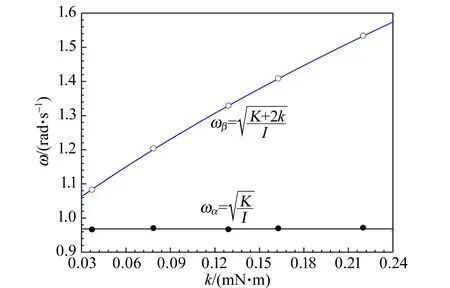
圖4 簡正頻率隨中段鋼絲扭轉系數k的變化
下面依據實驗原理對兩轉盤的初始轉角做特殊設置,觀測對稱簡正模、反對稱簡正模和拍. 將上下段鋼絲和中段鋼絲的扭轉系數分別設置為0.291 9 mN·m和0.037 1 mN·m,由表2可知簡正頻率的理論值分別為ωα=0.968 1 rad/s和ωβ=1.084 rad/s. 將兩轉盤旋轉至相同轉角后同時釋放,得到兩轉盤轉角的時間演化數據,如圖5所示.
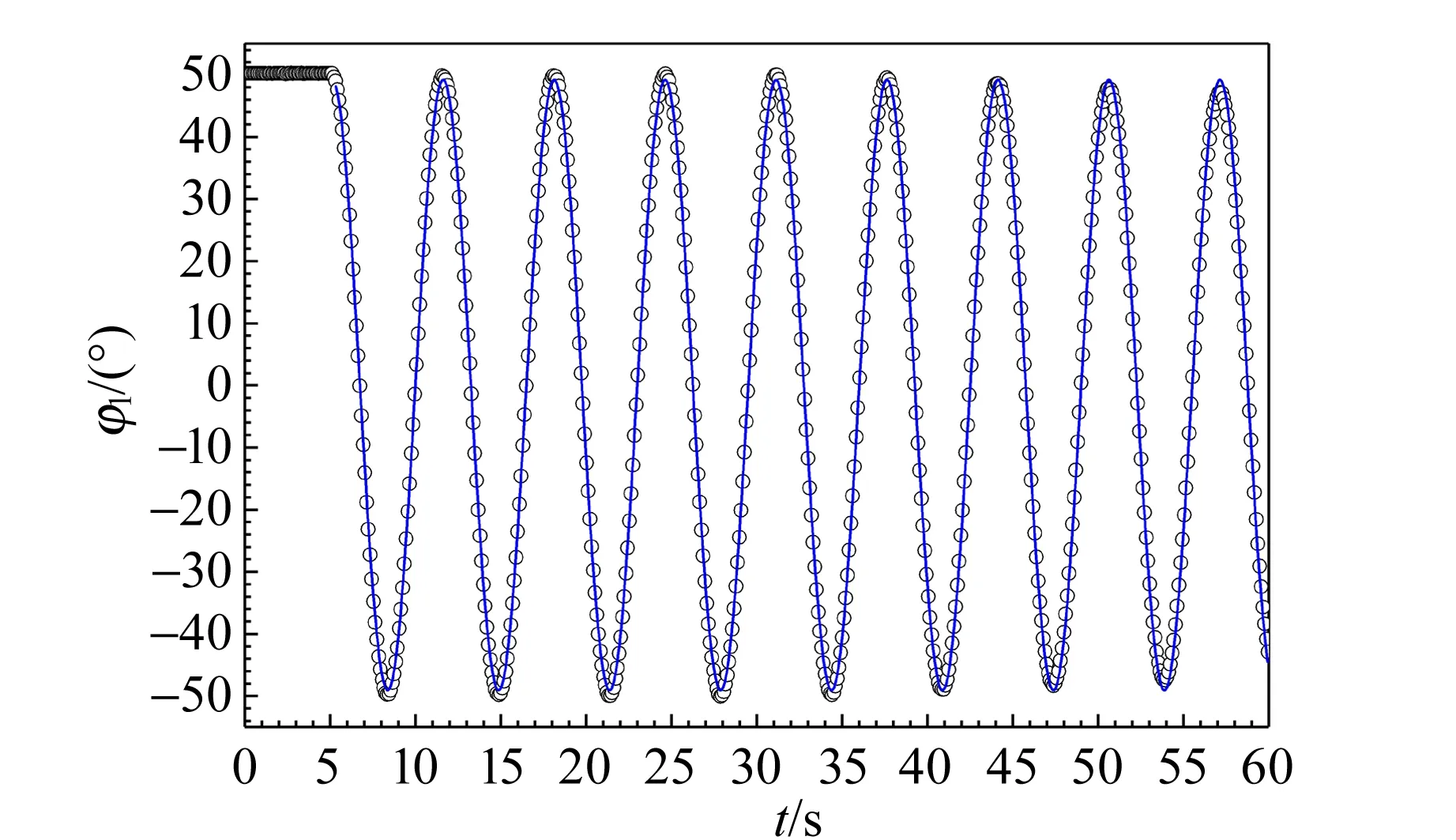
(a)上轉盤
從圖5可以看出,兩轉盤起初均靜止于轉角約50°處. 在被同時釋放后,轉角開始隨時間振蕩,并且幾乎同步增加或減小. 在60 s的觀測窗口內,兩轉盤的轉角振蕩幅度基本維持恒定,說明該體系的阻尼作用極小. 對振蕩部分的數據進行正弦擬合,結果如表3所示.

表3 圖5中兩轉盤轉角-時間演化曲線的正弦擬合結果[擬合函數φ=Asin (ωαt+ɑ)]
實驗數據和正弦曲線符合良好,兩轉盤都近似做簡諧轉動;兩轉盤的轉動幅度、頻率和相位基本一致,表明兩轉盤的轉動較好地呈現了對稱簡正模的主要特征. 另外,兩轉盤轉動角頻率的擬合結果與理論值接近,相對偏差均低于0.3%.
為了觀測反對稱簡正模,將兩轉盤旋轉至相反轉角后同時釋放,按實驗操作方法得到轉盤轉角的時間演化數據,如圖6所示.
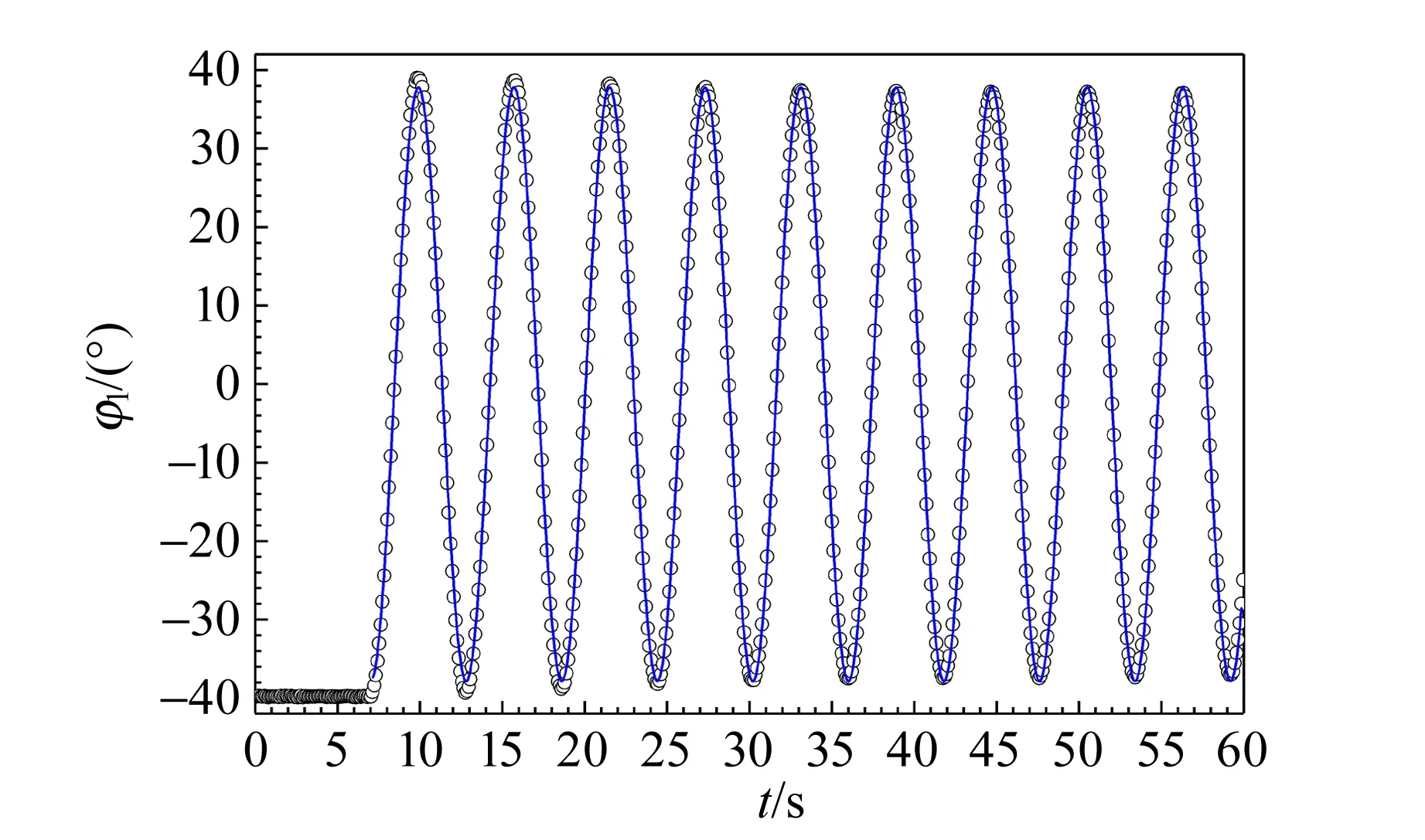
(a)上轉盤
從圖6可以看出,兩轉盤被釋放后,轉角開始隨時間振蕩,而且當上轉盤的轉角增加時,下轉盤的轉角同步減小;當上轉盤的轉角減小時,下轉盤的轉角同步增加. 在60 s的觀測窗口內,兩轉盤的轉角幅度均未發生明顯衰減,說明該體系的阻尼作用極小. 對振蕩部分的數據進行正弦擬合,結果如表4所示.
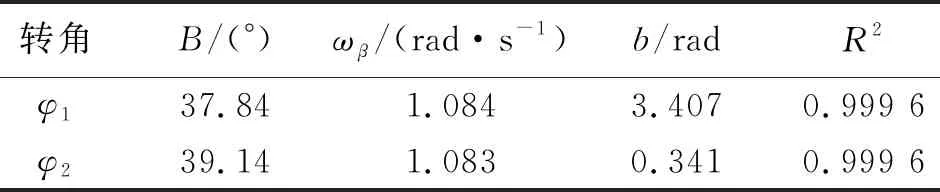
表4 圖6中兩轉盤轉角-時間演化曲線的正弦擬合結果[擬合函數φ=Bsin (ωβt+b)]
實驗數據和正弦曲線符合良好,兩轉盤都近似做簡諧轉動;兩轉盤的轉動幅度和角頻率基本一致,相位差約為π;兩轉盤轉動角頻率的擬合結果與理論值接近,相對偏差均低于0.1%. 上述結果表明,兩轉盤的轉動較好地呈現了反對稱簡正模的主要特征.
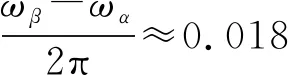
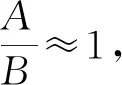

表5 圖7中轉盤轉角-時間演化曲線的雙正弦擬合結果[擬合函數φ=Asin (ωαt+a)+Bsin (ωβt+b]
5 結束語
本文類比固定端/彈簧/質塊/彈簧/質塊/彈簧/固定端系統設計了對稱雙扭擺實驗,使用手機錄制轉盤的一般耦合轉動以及對稱簡正模、反對稱簡正模和拍等特殊耦合轉動的視頻,運用目標追蹤軟件從中提取轉盤轉角的時間演化數據,通過數據擬合得到耦合轉動的幅度、頻率和相位等信息,實驗結果與理論預期符合良好. 教學實踐表明,該實驗有助于學生直觀地學習耦合振動的基本原理,激發實驗興趣.

