永磁吸附履帶式管外爬行機器人的力學分析及運動仿真

蔣怡蔚，侯宇，李浩男，孫偉

(1.武漢科技大學冶金裝備及其控制教育部重點實驗室，湖北武漢 430081；2.武漢科技大學機械傳動與制造工程湖北省重點實驗室，湖北武漢 430081；3.武漢科技大學精密制造研究院，湖北武漢 430081)

0 前言

工業管道作為城市中重要的運輸工具，需長期輸送高溫、高壓、有毒和有輻射的流體介質，一旦發生泄漏，將會造成重大的人員傷亡和財產損失。且工業管道所處環境復雜，人工檢測難度大，因此研究代替人工作業的管道機器人具有重要的學術研究價值和應用前景[1-2]。

在大量應用鋼制管道的工業現場，采用磁吸附方式的管道機器人具有更好的負載能力和運動穩定性，目前也最具有應用前景。實際應用中需要機器人具備以下功能：沿著管道進行軸向和周向運動，能通過焊縫、法蘭等障礙，具有良好的負載能力和運動穩定性。而這對管道機器人的磁吸附結構設計、越障機構設計、考慮磁吸附力的動力學特性等提出了很高的要求。關于磁吸附管外機器人的研究主要分為2個方面：磁吸附結構設計以及機器人的結構設計。趙軍友等[3]設計了一種由新型電磁吸附單元連接而成的吸附履帶結構，其負載能力強，但運動靈活性一般，不適合全方位檢測工作。邱仕誠等[4]設計了一種基于磁力吸附的儲罐爬壁機器人，采用永磁輪結構和輔助吸附裝置，在兩者共同作用下提高了機器人穩定性和負載能力。駱楊等人[5]設計了一種爬壁機器人，其永磁吸附組件固定在履帶鏈節上，在行走的過程中，保證單邊至少有10個永磁吸附組件與作業面接觸以提供足夠的吸附力。永磁吸附和電磁吸附作為磁吸附的2個分支，永磁吸附具有磁力持久、不受電源影響、便于維護等特點[6-7]，在實際應用中更具優勢。

對于永磁吸附式管外機器人的研究有很多，如：TAVAKOLI等[8]提出的Omniclimber敏捷型機器人，采用三角放置的磁吸附萬向輪，可以實現任意曲面方向的運動攀爬；HU等[9]設計了一種磁性爬壁機器人，采用四連桿結構設計骨架，可被動適應曲面；山東科技大學陳廣慶等[10]設計了一種履帶式鋼質壁面攀爬機器人，該機器人可沿中心軸旋轉一定角度，可適應外壁面的弧度。上述機器人都能適應管徑變化，但越障性一般。王洋等人[11]研制了一種基于分體柔性履帶移動與間隙式永磁吸附的自適應爬壁機器人，利用具有翻轉與俯仰2個自由度的連接模塊實現機器人的姿態變化以適應曲面，也可借助間隙式吸附結構的旋轉實現對焊縫等低障礙的跨越。但是對于管道上的法蘭盤等較高障礙，以上機器人依然難以實現有效越障。

對于永磁吸附履帶式管外爬行機器人，其主要的問題是：如何提高機器人對于管道的適應性以及兼顧機器人的可靠吸附與靈活運動[12-13]。針對以上問題，本文作者設計一種永磁吸附履帶式管外爬行機器人。首先，建立機器人在軸向和周向運動的力學模型并分析其安全吸附力；其次，通過Ansoft Maxwell軟件對磁性履帶組進行仿真分析；最后，利用ADAMS軟件對機器人的越障過程進行運動仿真，并分析仿真結果，為研究機器人的越障能力提供依據。

1 管道機器人總體設計

永磁吸附履帶式管外爬行機器人的總體結構如圖1所示，由前后2個相同的移動模塊通過鉸鏈連接而成。移動模塊的結構如圖2所示，由車體、履帶電機、輔助吸附調節機構、磁性履帶組和旋轉電機組成。磁性履帶組與車體通過鉸鏈連接，通過改變磁性履帶組與車體之間的角度，可適應一定范圍內管道曲率的變化。輔助吸附調節機構上固定連接著若干個永磁鐵，通過控制電動推桿的伸縮可調節永磁鐵與管壁之間的磁隙距離，達到調節磁力的目的。

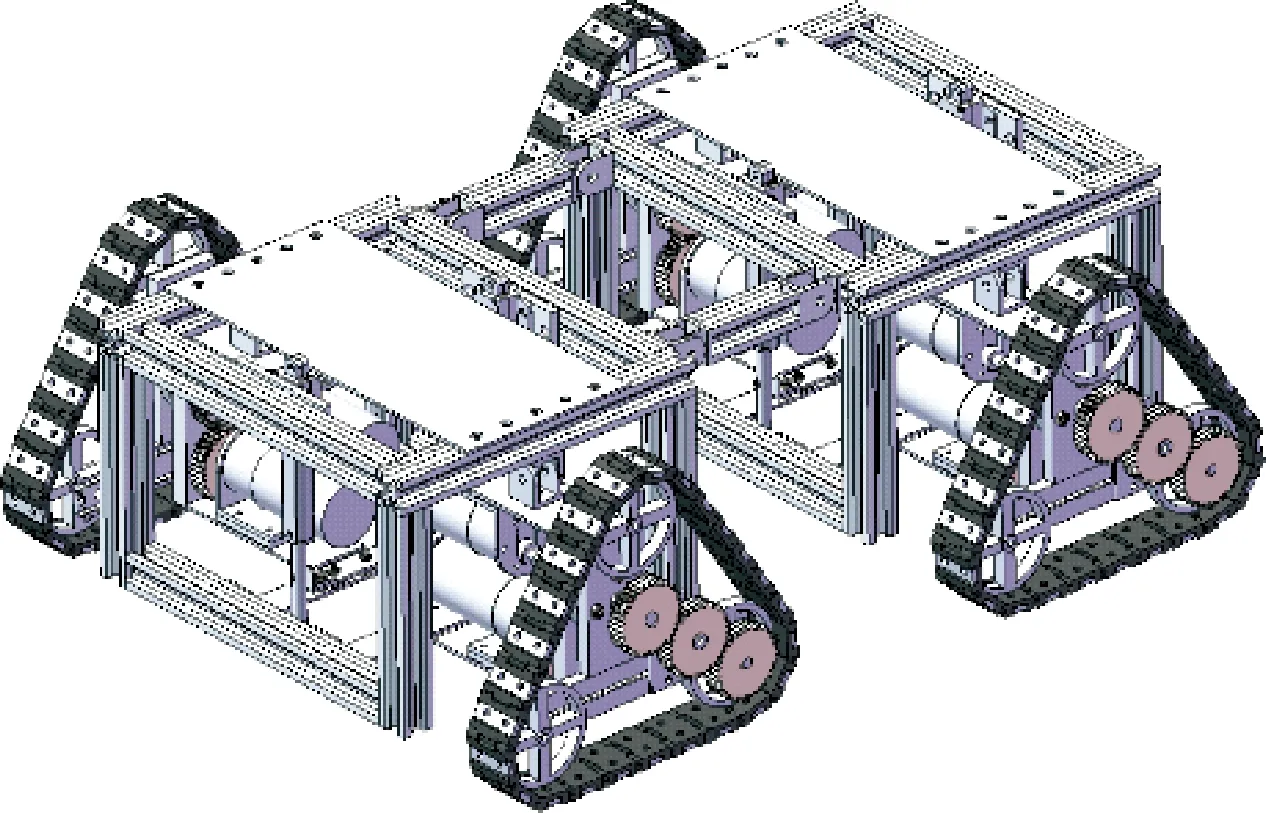
圖1 永磁吸附履帶式管外爬行機器人總體結構Fig.1 Permanent magnet adsorption crawler-type out- of-pipe crawling robot overall structure

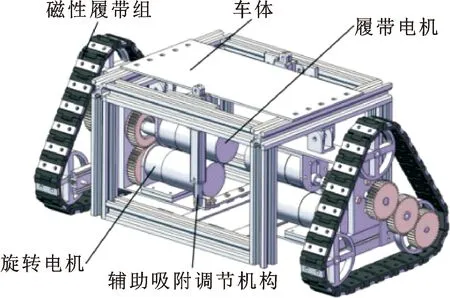
圖2 移動模塊結構Fig.2 Mobile module structure

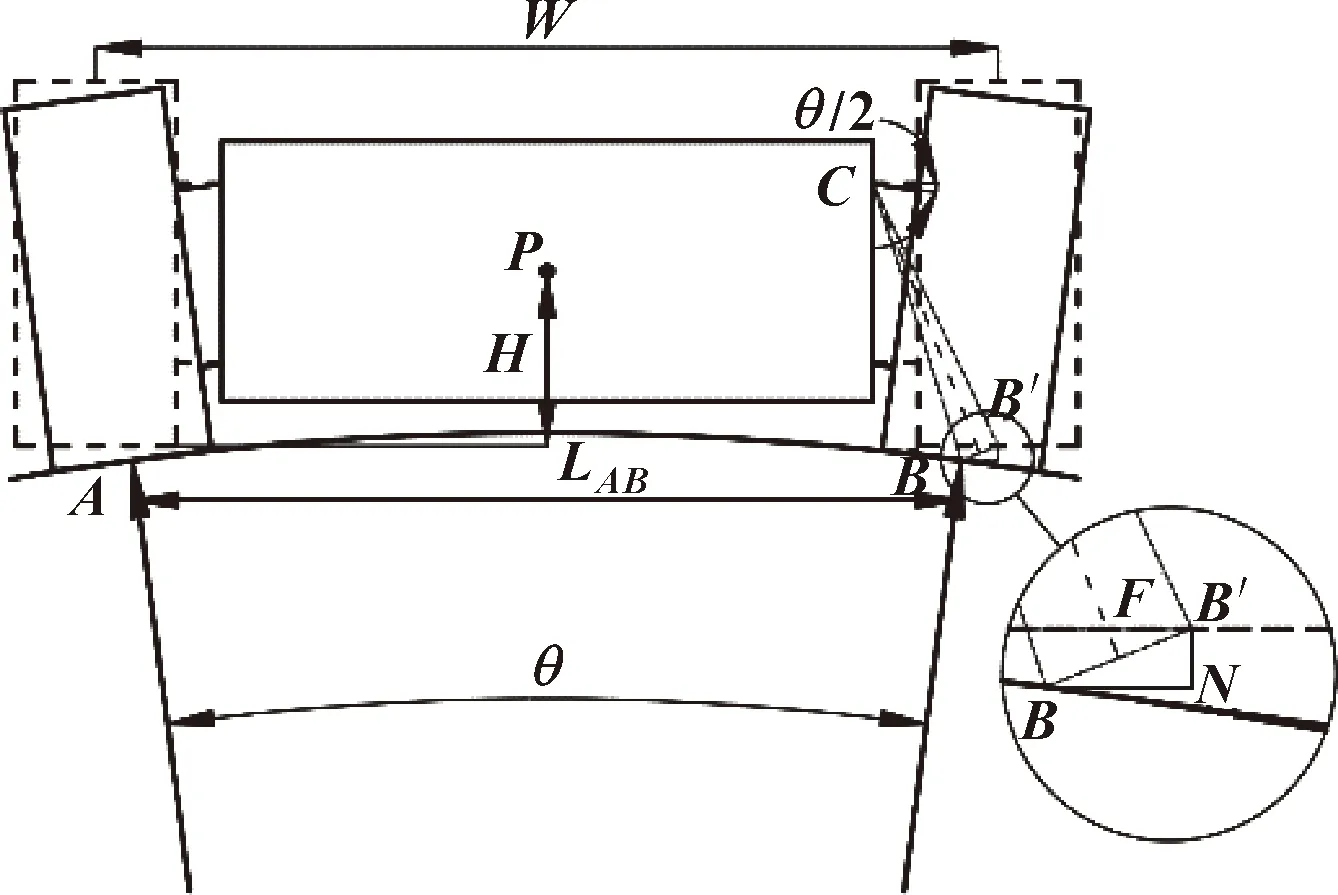
圖3 機器人適應管道結構示意Fig.3 Schematic of robot adapting to pipe structure

如圖3所示，其中△CB′B為等腰三角形，連接點C與B′B的中點F，可得：

(1)

(2)

(3)

式中：LB′C為B′C的距離；HB′C為B′C的垂直距離；φ1為B′C與水平線之間的夾角；θ/2為磁性履帶組由位置1到位置2旋轉角度；φ2為∠CB′B。

LBN=cos(φ2-φ1)LBB′

(4)

(5)

式中：LAB為切點AB之間的距離；R為管道半徑；W為位置1時兩側磁性履帶組的底部中心距離，即機器人的寬度。

已知LB′C、HB′C、R以及W的條件下，聯立式(1)—(5)可求得磁性履帶組的旋轉角度θ/2與管道半徑R之間的關系：

2Rsinθ/2=W-4cos[π/2-θ/4-

arcsin(HB′C/LB′C)]sin(θ/4)LB′C

(6)

同時可求得磁性履帶組由位置1到位置2時，機器人在垂直方向的移動距離，即為LB′N。

(7)

H1=H+LB′N

(8)

式中：H為位置1時質心點P到履帶底部的垂直距離；H1為位置2時質心點P到履帶底部的垂直距離。

2 管道機器人力學建模分析

2.1 靜力學建模

機器人在管道上運動失穩的情況分別為沿管壁向下滑移和沿下接觸點發生傾覆。下面以單節移動模塊為研究對象，分別在沿管道軸向和周向運動的2種情況下建立管外爬行機器人下滑和傾覆的力學模型并進行分析，為后續機器人吸附力的設計提供理論依據。

2.1.1 機器人沿管道軸向運動

對機器人沿管道軸向運動進行受力分析，如圖4所示，定義Oxy為坐標系，坐標原點O與質心P重合。

圖4 機器人軸向運動受力分析Fig.4 Force analysis of robot axial motion：(a)force diagram；(b)vector diagram

(1)軸向滑移分析

機器人沿軸向運動時，以不發生滑移的極限情況進行分析可得下式：

(9)

式中：FmL、FmR分別為機器人兩側磁性履帶組所提供的吸附力，且Fm=FmL=FmR；fL、fR分別為機器人兩側磁性履帶組與管壁之間的摩擦力，且fL=μNL，fR=μNR；μ為磁性履帶組與管壁的靜摩擦因數；NL、NR分別為機器人兩側磁性履帶組的支持力；G為單節移動模塊的重力；α為機器人的質心P和管道圓心的連線與垂直線之間的角度，當機器人在管道頂部時，α=0。

由式(9)得：

NR-NL=X1=

(10)

NL+NR=X2=

(11)

(12)

(2)軸向傾覆分析

若機器人繞點B傾覆，處于即將發生傾覆的臨界狀態時，NL=0。此時移動模塊應滿足以下條件：

(13)

由式(13)得：

(14)

2.1.2 機器人沿管道周向運動

(1)周向滑移分析

對機器人沿管道周向運動進行受力分析，如圖5所示。

以單側磁性履帶組不發生滑移的極限情況進行分析可得下式：

(15)

式中：i為單側磁性履帶組接地段永磁吸附單元的數量；Ni為單側磁性履帶組上單個永磁吸附單元的支持力；Fmi為單側磁性履帶組上單個永磁吸附單元所提供的吸附力，Fm=FmL=FmR=∑Fmi；βi為單個永磁吸附單元與管道切線的夾角；fi為單側磁性履帶組上單個永磁吸附單元與管壁的靜摩擦力。

由圖5可知：

(16)

式中：d為磁性履帶組底部兩履帶輪之間的距離；LDE為機器人與管道的切點DE之間的距離；r為磁性履帶組中履帶輪的半徑；β為機器人接地段所對應的圓心角。由于R遠遠大于d，則β可忽略不計。由式(15)可得：

(17)

(2)周向傾覆分析

以機器人單側磁性履帶組為例進行分析，若機器人繞點E傾覆，處于即將發生縱向傾覆的臨界狀態時，點D處的支持力ND為零，即ND=0。其中β忽略不計，則單側磁性履帶組應滿足以下條件：

(18)

式中：FmD為單側磁性履帶組中點D處永磁吸附單元的吸附力。由式(18)得：

(19)

機器人參數初步取G=30 N、R=1 m、W=345 mm、H=85 mm、d=128 mm、LB′C=155 mm、HB′C=136 mm、μ=0.8、i=7。由式(1)—(8)可得到θ、H1、LAB，通過MATLAB計算得出機器人在管道上穩定工作時所需要的極限吸附力和位置角度α之間的關系，取α=[0°，180°]。當吸附力小于零時，表明此時不需要吸附力作用便可保持機器人不下滑或不傾覆。

如圖6(a)所示，當機器人軸向運動時，在位置角度α=126°處，機器人保持不滑移的極限吸附力最大，單側磁性履帶組所需提供極限吸附力為25.890 9 N；在位置角度α=146°處，機器人保持不傾覆的極限吸附力最大，單側磁性履帶組所需提供極限吸附力為18.4471 N。

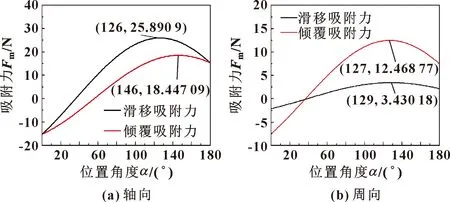
圖6 吸附力與位置角度α關系Fig.6 Relationship between adsorption force and position angle α：(a)axial direction；(b)circumferential direction

如圖6(b)所示，當機器人周向運動時，在位置角度α=129°處，機器人保持不滑移的極限吸附力最大，單個永磁吸附單元所需提供極限吸附力為3.430 2 N，單側磁性履帶組所需提供極限吸附力為24.011 4 N；在位置角度為α=127°處，機器人保持不傾覆的極限吸附力最大，單個永磁吸附單元所需提供吸附力為12.468 8 N，單側磁性履帶組所需提供極限吸附力為87.281 6 N。

綜上所述，機器人在管道上穩定運行時需滿足的條件為：沿軸向運動時，單側磁性履帶組提供的最小吸附力應大于25.890 9 N；沿周向運動時，單側磁性履帶組提供的最小吸附力應大于87.281 6 N。

2.2 動力學建模

為便于機器人的動力學建模，做出以下假設：(1)機器人的質心和幾何中心在壁面上投影重合；(2)履帶在其運動方向上不打滑；(3)單條履帶的接地段壓力均勻分布。

2.2.1 機器人沿管道軸向運動

對機器人沿軸向運動進行受力分析，如圖7所示。以機器人的質心P為坐標原點OP建立坐標系OPxPyP，設定xP為垂直于機器人運動方向，yP為機器人運動方向。

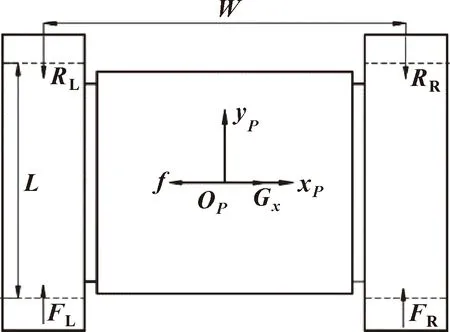
圖7 機器人軸向運動受力分析Fig.7 Force analysis of robot axial motion

建立其動力學運動方程：

(20)

由式(9)可得：

(21)

(22)

聯立方程組可得：

(23)

(24)

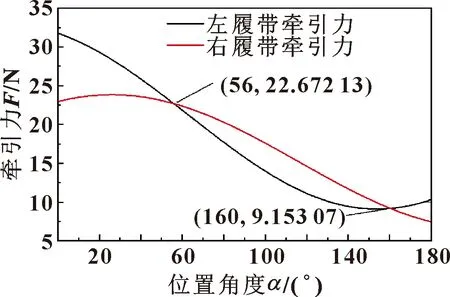
圖8 軸向運動時牽引力與位置角度的關系Fig.8 Relationship between traction force and position angle during axial motion

2.2.2 機器人沿管道周向運動分析

對機器人沿周向運動進行受力分析，如圖9所示。

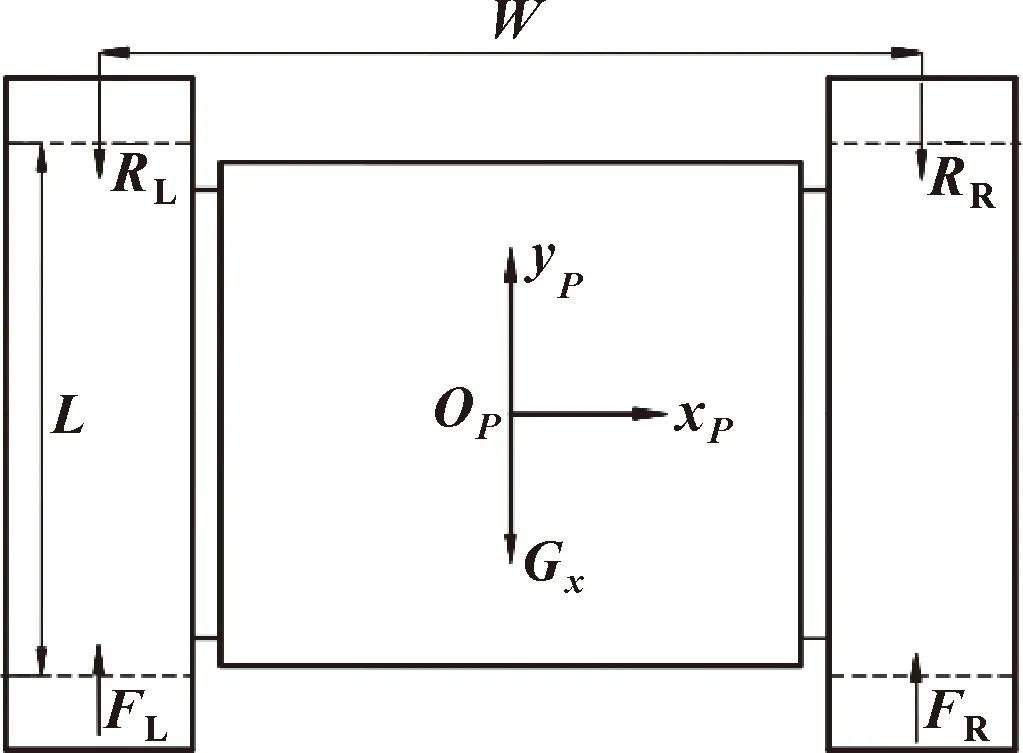
圖9 機器人周向運動受力分析Fig.9 Force analysis of robot circumferential motion

由于機器人為對稱結構，因此機器人兩側磁性履帶的支持力和摩擦力相同。其動力學運動方程為

(25)

式中：

(26)

如圖10所示，對機器人垂直于管道壁面的方向建立力平衡方程：

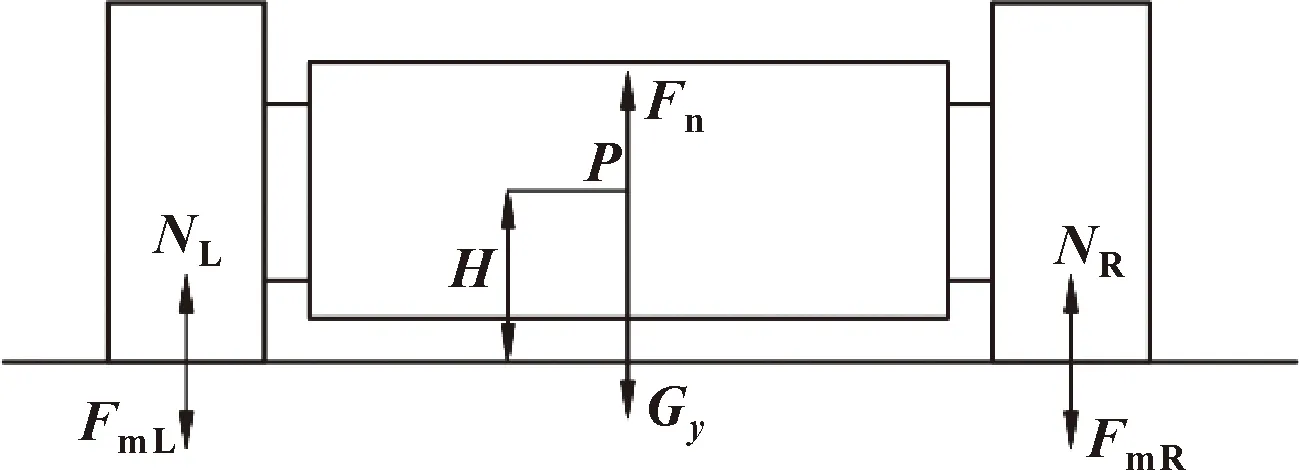
圖10 機器人周向運動時垂直管壁受力分析Fig.10 Analysis of vertical pipe wall forces during robot circumferential motion

(27)

式中：Gy為機器人在y方向上的重力分力；Fn為離心力。

由式(27)得：

Fm+Gcosα-mv2/R)×1/2

(28)

式中：v為機器人的移動速度。

由式(25)—(28)可得：

(29)

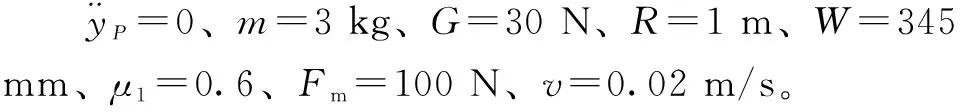
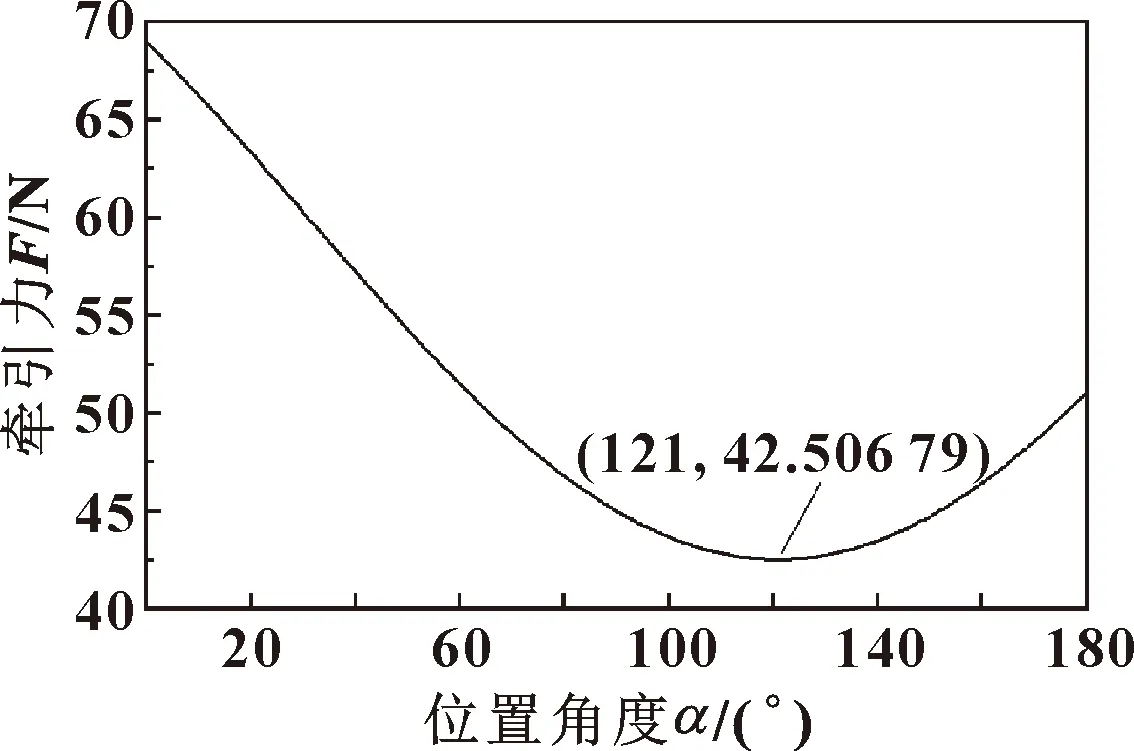
圖11 周向運動時牽引力與位置角度的關系Fig.11 Relationship between traction force and position angle during circumferential motion

3 磁吸附結構設計與分析

3.1 永磁鐵布局設計分析

永磁鐵固定在每個橡膠履塊上，橡膠履塊相互連接構成了磁性履帶組。這種結構既保證了機器人運動的傳遞，也保障了機器人在爬行過程中所需的吸附力，提高了機器人在管道外壁運動的穩定性。

為使永磁鐵得到更充分的利用，在原有結構基礎上，設計了2種永磁鐵的布局方式。方案中永磁鐵均采用厚度方向充磁，方案一(圖12(a))為永磁鐵采用同一充磁方向，方案二(圖12(b))為相鄰永磁鐵的充磁方向相反。

取永磁鐵的尺寸為30 mm×10 mm×3 mm，磁隙距離設定為1 mm。利用Ansoft Maxwell軟件對磁性履帶組進行仿真，其步驟為：依據現有結構尺寸建立二維模型；定義材料屬性(永磁材料選取FdFeB-N35，并設置各永磁鐵充磁方向；管道選取鋼鐵Steel-1008；磁隙介質為空氣，相對磁導率μr=1.0)；對幾何模型進行網格劃分并施加邊界條件；設置合適的求解參數進行求解；進行后處理得到相應的磁力線分布，如圖13所示。

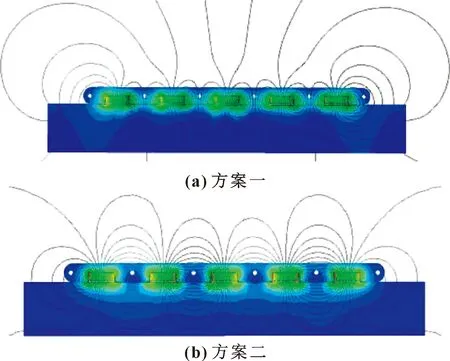
圖13 磁力線分布Fig.13 Distributions of magnetic field lines：(a)scheme 1； (b)scheme 2

對比可知：

(1)磁化方向垂直于壁面的磁體產生的磁感線，通過空氣磁隙進入壁面再回到磁體，產生吸附力[14]。方案一的磁力線主要集中在履帶兩側，通過壁面的磁力線較少；方案二的磁力線主要集中在上下兩側，對管道的吸附力更強。

(2)對比磁感應強度分布情況，方案二在鋼質壁面上產生的磁感應強度比方案一分布得更均勻、密度更大，這保證了吸附力均勻分布。

(3)2種方案在空氣中都存在漏磁，可在永磁鐵上部添加軛鐵，利用軛鐵的聚磁效應，減少永磁吸附單元上部分漏磁和磁能量的損耗[15-16]。文中由于結構局限，故不考慮添加軛鐵。

3.2 仿真分析及結構參數分析

運用Ansoft Maxwell軟件將磁性履帶組模型從SolidWorks軟件中轉換格式并導入分析。其中周向運動時，因履帶為柔性，在建模中需使磁性履帶貼合在管道上。

通過仿真分析得到2種方案下的軸向和周向運動時的吸附力，如表1所示。

由表1可得：上述2種方案都能夠滿足機器人在管道上穩定運動的吸附力條件，方案二的吸附力要大于方案一。考慮到實際應用，選擇方案二作為文中機器人磁性履帶組的布局方案。

因機器人需要適應管道外壁的各種障礙，在此過程中磁性履帶組所產生的吸附力會發生變化。為進一步研究吸附力的變化，在軸向運動模型下對磁隙參數進行掃描，設定磁隙范圍為1～10 mm。磁隙與吸附力之間的關系如圖14所示。

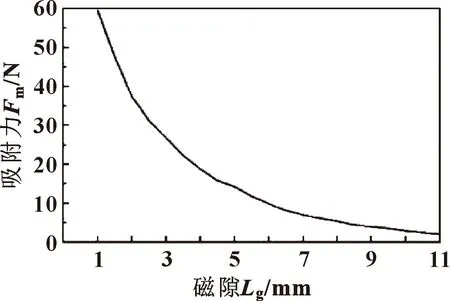
圖14 磁隙與吸附力的關系Fig.14 Relationship between magnetic gap and adsorption force

由圖14可知：隨著磁隙逐漸增大，吸附力減小，趨近于0。則當機器人在越障過程中，機器人會出現吸附力驟減的現象，因此需要借助輔助吸附調節機構使機器人保持穩定運行。

4 越障過程運動仿真

在ADAMS軟件中建立機器人虛擬樣機模型，其步驟為：將SolidWorks中建立的模型導入，設置單位、工作網格和重力等工作環境；設定各組件的名稱、顏色、材料屬性等信息，并定義各組件間的約束以及添加吸附力。虛擬樣機模型如圖15所示。

圖15 虛擬樣機模型Fig.15 Virtual prototype model

磁性履帶組采用三角履帶的結構，便于機器人適應管道上不同高度的障礙。下面對低障礙(焊縫等)和高障礙(法蘭盤等)2種情況分別討論。遇到焊縫等低障礙時，可直接通過。在運動仿真中設定低障礙的高度為10 mm，單側磁性履帶組所提供的吸附力為30 N。越障過程如圖16所示。

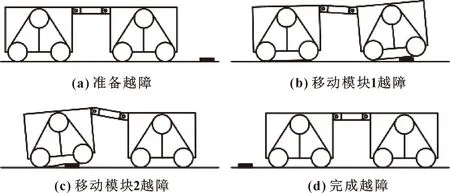
圖16 機器人跨越低障礙過程Fig.16 Robot crossing low obstacle process：(a)prepare to overpass obstacle；(b)mobile module 1 overpass obstacle；(c)mobile module 2 overpass obstacle； (d)complete obstacle crossing

機器人在通過低障礙過程中的2個移動模塊質心的變化趨勢，如圖17所示。可知：2個移動模塊的質心變化趨勢相似，且與障礙物的形狀相近。履帶的柔性特質使機器人在越障過程中其質心位移比障礙物低，且造成了質心位移的波動。這驗證了機器人具有良好的穩定性以及越障性。

遇到法蘭盤等高障礙時，磁性履帶組可相對于車體整體旋轉，提高了機器人整體的越障性。設定高障礙的高度為50 mm，吸附力不變，其越障過程如圖18所示。

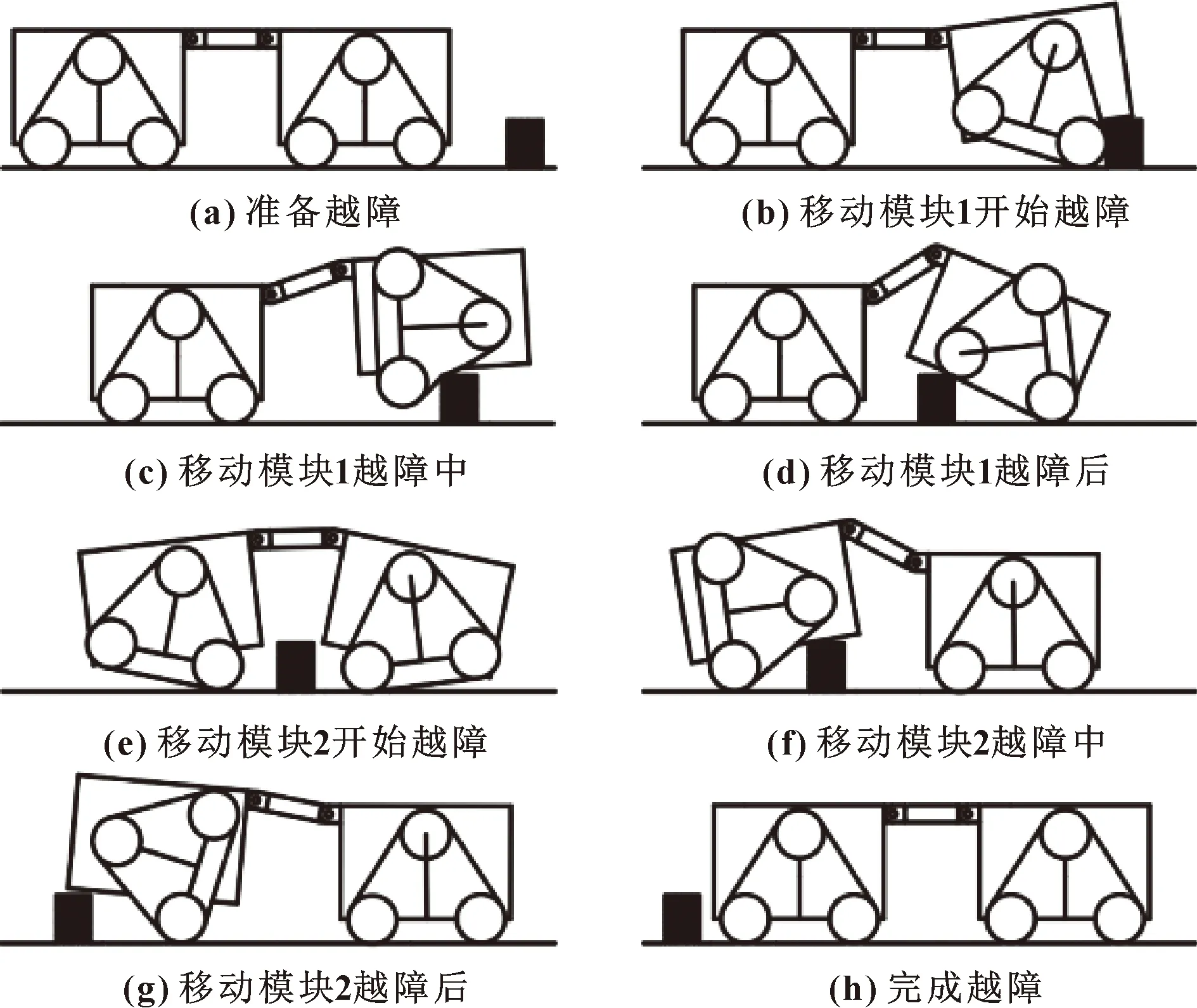
圖18 機器人跨越高障礙過程Fig.18 Robot crossing high obstacle process：(a)prepare to overpass obstacle；(b)mobile module 1 starts to overpass obstacle；(c)mobile module 1 is overpassing obstacle；(d)mobile module 1 overpass obstacle； (e)mobile module 2 starts to overpass obstacle； (f)mobile module 2 is overpassing obstacle； (g)mobile module 2 overpass obstacle； (h)complete overpass obstacle

當機器人即將遇到障礙時，移動模塊1的磁性履帶組相對于車體順時針旋轉，準備越障；當磁性履帶組接觸到障礙物時，磁性履帶組以兩者的接觸點為旋轉中心旋轉，直至移動模塊1越過障礙；同時移動模塊2的磁性履帶組相對于車體旋轉，重復移動模塊1的運動過程，直至移動模塊2跨越障礙；機器人完成了整個越障動作。

機器人通過高障礙過程中的2個移動模塊質心的變化趨勢如圖19所示。其質心變化趨勢與障礙物的高度基本一致，從而驗證了機器人具有良好的越障性能。

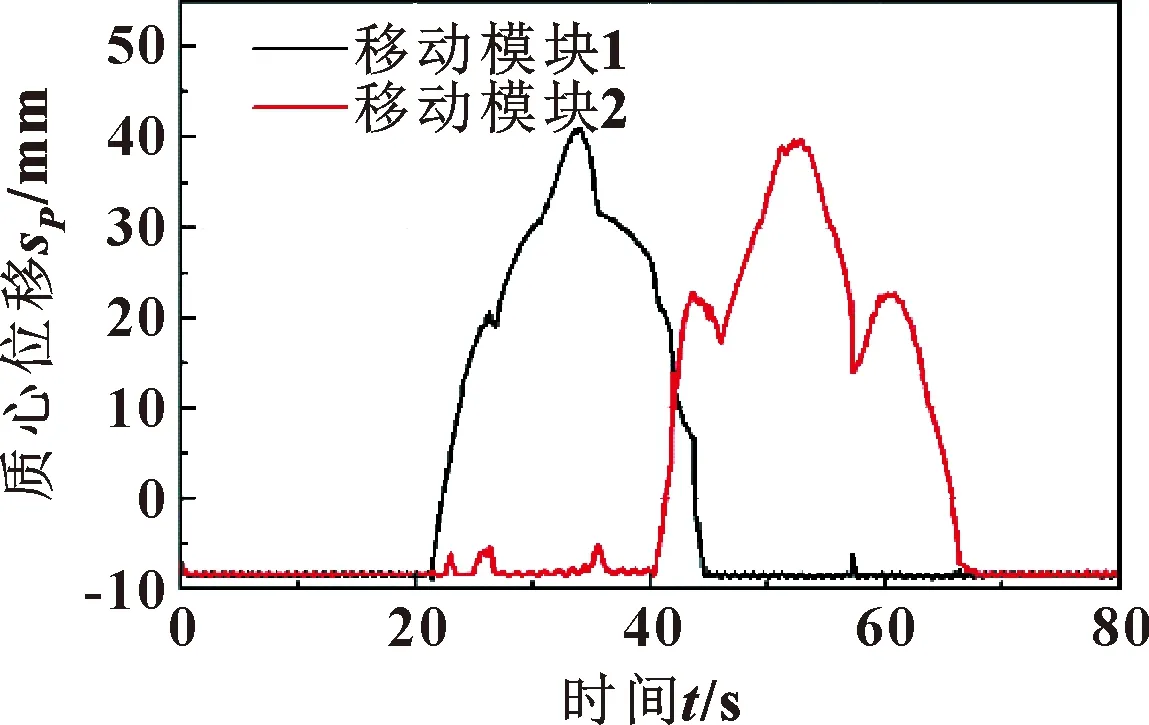
圖19 機器人越高障礙時移動模塊質心變化Fig.19 The centroid changes of the moving module when the robot crosses high obstacle

5 總結

(1)設計了一種永磁吸附履帶式管外爬行機器人，其具有較強的適應性和負載能力；推導出管道直徑與機器人結構尺寸之間的關系，為機器人的詳細設計提供了理論基礎。

(2)建立機器人在管道上軸向和周向運動的靜力學和動力學模型，得到了該機器人穩定工作時的吸附力條件，以及該條件下軸向和周向運動時的牽引力和位置角度的變化關系。

(3)通過Ansoft Maxwell建立磁性履帶組的模型，對比分析了2種不同永磁鐵布局方式，選定了合適的布局方案；計算軸向和周向運動時吸附力的大小，其結果滿足機器人的吸附力條件，驗證了磁性履帶組結構的可行性。

(4)通過ADAMS進行越障的動力學仿真，分析了機器人在10 mm和50 mm 2種障礙物高度下越障過程中的質心變化，驗證了機器人具有良好的越障性能。