機器人氣動夾持力的CNN-LSTM建模估計方法

黨選舉，覃創(chuàng)業(yè)

(桂林電子科技大學電子工程與自動化學院，廣西桂林 541004)

0 前言

目前，裝備氣動執(zhí)行末端的工業(yè)機器人越來越廣泛地應用于工業(yè)制造、交通運輸?shù)阮I域[1]。然而，氣動夾持系統(tǒng)受氣體可壓縮性、系統(tǒng)固有的非線性摩擦以及氣路的收縮等影響，使得系統(tǒng)輸入氣壓與輸出夾持力之間存在強非線性遲滯特性[2]，從而導致工業(yè)機器人氣動末端在開環(huán)控制下無法確保夾持力控制精度。因而需通過夾持力檢測提高機器人氣動夾持系統(tǒng)控制性能。但傳統(tǒng)夾持力檢測方法依賴于力傳感器，存在成本增加、易受電磁干擾等問題[3]。因此，無傳感器夾持力建模估計方法有利于提高工業(yè)機器人氣動末端夾持控制精度[4]，并可減少系統(tǒng)成本、提高系統(tǒng)可靠性，具有重要的研究意義。

近年來，諸多學者針對機器人氣動末端無傳感器夾持力估計展開了研究。例如，文獻[5]以氣動機器人動力學模型為基礎，提出一種基于夾持系統(tǒng)機制模型的無傳感器夾持力估計方法；文獻[6]針對氣動肌肉使能的機器人系統(tǒng)，提出一種基于自適應增益積分終端滑模控制的無傳感器力估計方案。此外，為提高系統(tǒng)在擾動情況下的估計效果，又提出了一種時變自適應最優(yōu)力估計方案[7]，采用延時估計法對系統(tǒng)中的非線性和擾動進行近似估計，以減少系統(tǒng)摩擦的影響。然而，氣動系統(tǒng)易受環(huán)境干擾，系統(tǒng)模型參數(shù)具有時變性，導致上述方法難以獲取精確的模型參數(shù)，且模型計算復雜。為了克服上述缺點，文獻[8]針對機器人氣動末端力估計問題，提出一種基于神經(jīng)網(wǎng)絡的夾持力估計方案，利用神經(jīng)網(wǎng)絡建模實現(xiàn)夾持力估計，該方法更簡單有效，但當氣壓壓力變化時，模型的估計精度會降低。且氣動夾持系統(tǒng)固有的非線性特性使得基于單一神經(jīng)網(wǎng)絡的力估計方法難以獲得準確的估計結果。文獻[9]提出了一種基于遺傳算法優(yōu)化的神經(jīng)網(wǎng)絡夾持力估計方案；文獻[10]使用PSO優(yōu)化BP神經(jīng)網(wǎng)絡，并結合扭矩擾動觀測器，實現(xiàn)最終夾持力估計。該類方法相比單一網(wǎng)絡，可提高估計精度。但以上方法未考慮到氣動系統(tǒng)特有的遲滯強非線性特性，且氣動遲滯特性會導致閉環(huán)系統(tǒng)的反饋作用減弱，限制了夾持力估計精度的進一步提高。

因此，針對工業(yè)機器人氣動夾持系統(tǒng)所呈現(xiàn)的復雜遲滯非線性特性，通過建模方法實現(xiàn)無力傳感器的低成本氣爪夾持力估計，是提高工業(yè)機器人氣動末端夾持控制精度、減少系統(tǒng)成本的有效途徑。本文作者從系統(tǒng)的角度，綜合考慮影響夾持力的各種干擾因素，并結合氣動工業(yè)機器人夾持力輸出與歷史輸入有關的特性，構建基于LSTM網(wǎng)絡的氣壓/夾持力估計模型。為進一步提高模型對系統(tǒng)多值對應特性的描述能力與估計精度，引入CNN特征提取層構建CNN-LSTM組合神經(jīng)網(wǎng)絡夾持力估計模型，實現(xiàn)一種低成本的基于模型的氣爪夾持力估計方法。

1 基于LSTM網(wǎng)絡的夾持力估計模型

1.1 氣爪夾持系統(tǒng)非線性特性分析

工業(yè)機器人氣爪夾持力控制系統(tǒng)如圖1所示，其中電氣比例閥作為氣壓控制模塊。

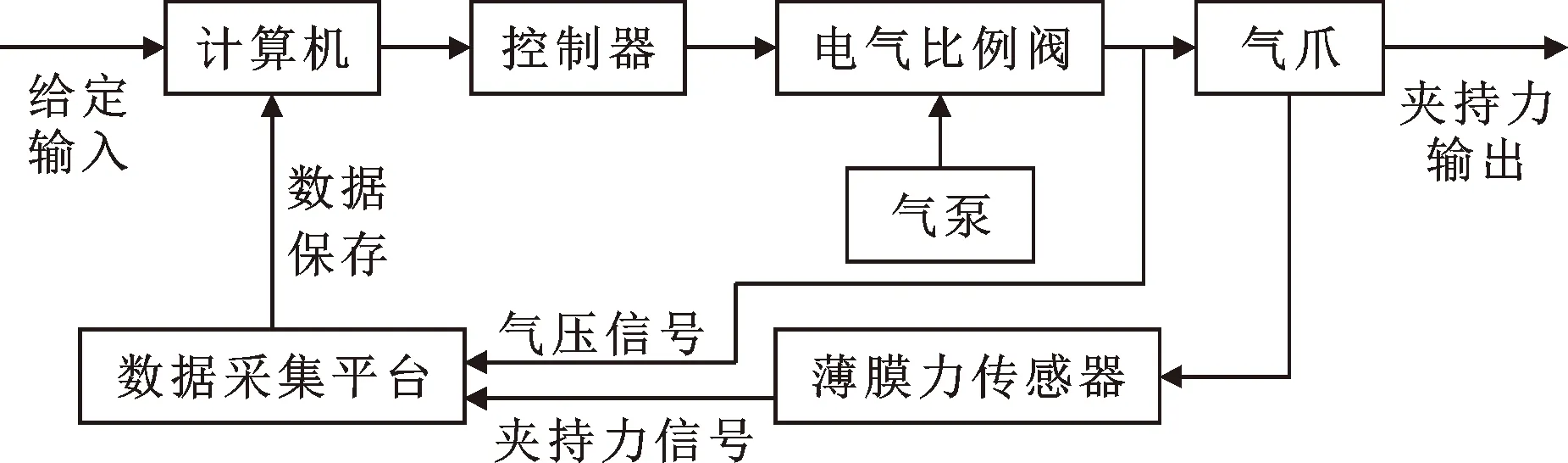
圖1 氣爪夾持系統(tǒng)結構Fig.1 The architecture of gripper system for pneumatic gripper

文中根據(jù)所搭建的實驗平臺采集氣爪夾持系統(tǒng)的實驗數(shù)據(jù)，并繪制輸入氣壓與輸出夾持力之間的關系曲線，如圖2所示。

由圖2與文獻[2]可知，氣動夾持系統(tǒng)的氣壓-夾持力遲滯現(xiàn)象具有如下特性：(1)在往復運動中存在多值對應特性，當氣壓輸入信號pa=pb時，所對應的夾持力Fa≠Fb；(2)氣路內(nèi)部的氣壓大小不僅由當前輸入氣壓pt決定，還取決于歷史輸入氣壓pt-1和歷史輸出夾持力Ft-1、Ft-2等。

1.2 長短期記憶網(wǎng)絡

長短期記憶網(wǎng)絡(LSTM)是基于循環(huán)神經(jīng)網(wǎng)絡(RNN)改進的一種模型，利用門限思想對記憶單元的狀態(tài)進行控制更新，解決了RNN訓練過程中的梯度消失和梯度爆炸問題[11]。LSTM核心在于其3個門限結構與記憶單元Ct，具體結構如圖3所示。

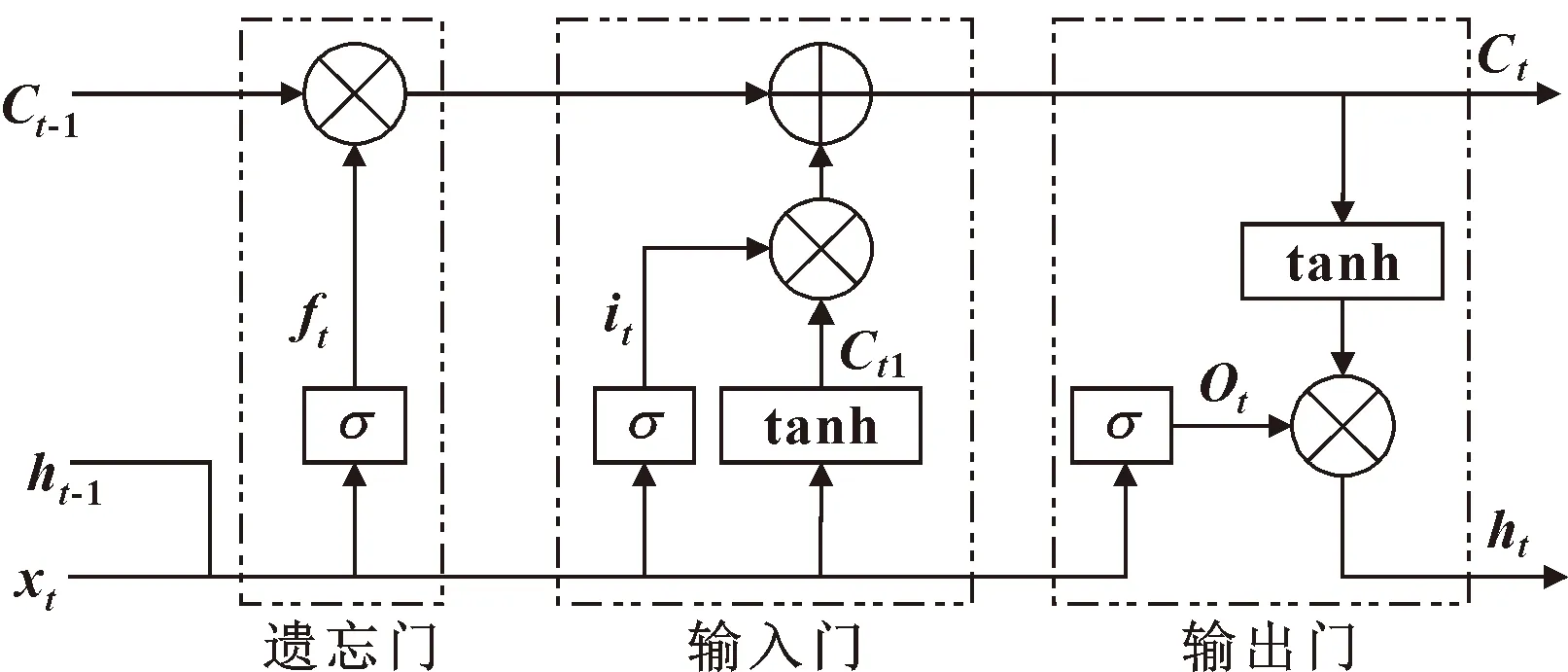
圖3 LSTM單元結構Fig.3 The architecture of LSTM cell

LSTM網(wǎng)絡通過輸入門、遺忘門和輸出門3個門提取重要的輸入信息，并將所提取到信息傳遞給記憶單元，更新記憶單元的記憶狀態(tài)。具體計算過程如下所示。

(1)LSTM網(wǎng)絡遺忘門

ft=σ(Wf，hht-1+Wf，xxt+bf)

(1)

σ(x)=1/[1+exp(-x)]

(2)

(2)LSTM網(wǎng)絡輸入門

it=σ(Wi，hht-1+Wi，xxt+bi)

(3)

Ct1=tanh(Wc，hht-1+Wc，xxt+bc)

(4)

(5)

(3)LSTM記憶單元

Ct=ft⊙Ct-1+it⊙Ct1

(6)

(4)LSTM網(wǎng)絡輸出門

Ot=σ(Wo，hht-1+Wo，xxt+bo)

(7)

(5)LSTM單元輸出

ht=Ot⊙tanh(Ct)

(8)

式中：xt為當前t時刻網(wǎng)絡輸入；ht-1為t-1時刻的LSTM網(wǎng)絡單元輸出；Wf，h、Wf，x、Wi，h、Wi，x、Wc，h、Wc，x、Wo，h和Wo，x分別為遺忘門、輸入門、當前輸入單元狀態(tài)Ct1和輸出門的權值；bf、bi、bc和bo為偏置；⊙為Hadamard乘積操作；σ(x)為Sigmoid函數(shù)；tanh(x)為tanh激活函數(shù)。

由式(1)—(8)得知，當前t時刻的輸出ht不僅與當前輸入xt有關，也與歷史輸出ht-1和記憶狀態(tài)Ct有關。

1.3 構建LSTM網(wǎng)絡夾持力估計模型

LSTM網(wǎng)絡相比傳統(tǒng)RNN具有更好的記憶功能，可以更有效地獲取氣壓-夾持力數(shù)據(jù)中的歷史關聯(lián)信息。因此文中采用LSTM網(wǎng)絡構建無力傳感器的夾持力估計模型，但數(shù)據(jù)在輸入到網(wǎng)絡模型中之前，需要先進行預處理。LSTM網(wǎng)絡夾持力估計模型結構示意如圖4所示。

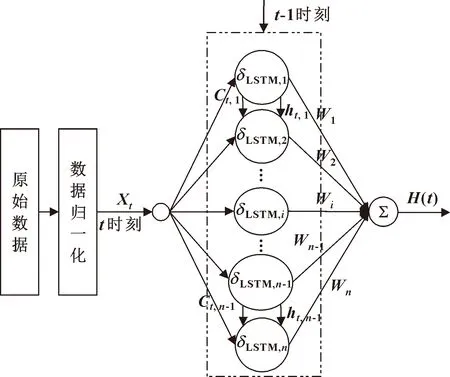
圖4 基于LSTM的夾持力估計模型Fig.4 Gripping force estimation model based on LSTM

考慮到氣路的過去行為也會影響工業(yè)機器人末端氣爪夾持力實際輸出，因此選擇t和t-1時刻的氣壓輸入信號pt、pt-1。并且為了使神經(jīng)網(wǎng)絡具有動態(tài)特性，將模型的t-1和t-2時刻的網(wǎng)絡估計值H(t-1)和H(t-2)，及其變化增量(E=H(t-1)-H(t-2))作為模型輸入信息Xt=(pt，pt-1，H(t-1)，H(t-2)，E)T。

如圖4所示，隱含層由n個LSTM單元組成，δLSTM，i表示隱含層的第i個LSTM單元節(jié)點，n=1，2，…，i，…，32，隱含層t時刻輸出為ht=(ht，1，ht，2，…，ht，i，…，ht，n)T。模型t時刻的輸出H(t)和損失函數(shù)分別如式(9)、(10)所示：

H(t)=Wht+b

(9)

Et=[Ft-H(t)]2/2

(10)

式中：W=(W1，W2，…，Wi，…，Wn)為輸出權重；b為偏置；Ft為t時刻夾持力目標值；H(t)為t時刻LSTM模型估計值。

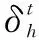
(11)

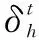
(12)

同理，輸入門、輸出門和隱含層也可根據(jù)反向推導計算出梯度。

使用2組不同的數(shù)據(jù)，分別對LSTM夾持力估計模型進行建模與估計驗證實驗，結果如圖5所示。

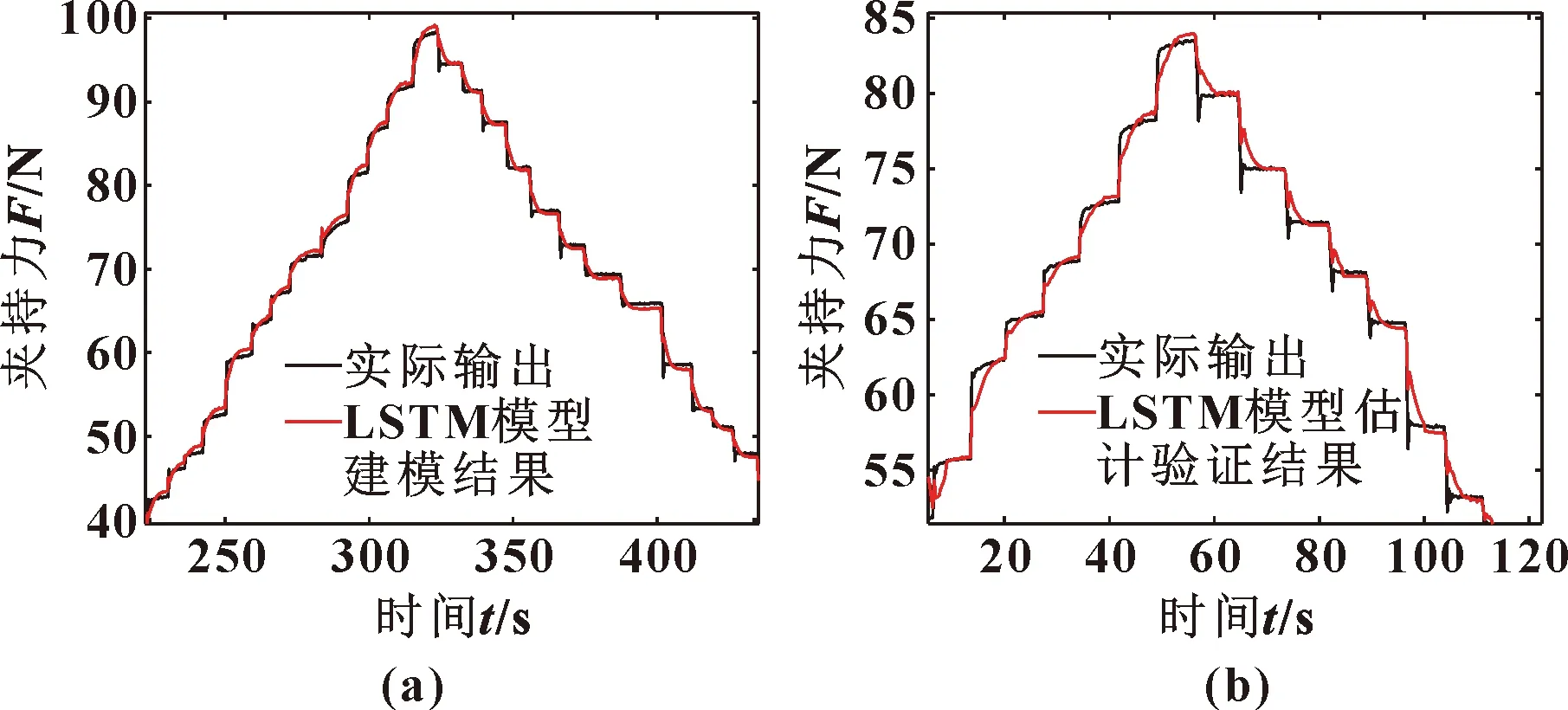
圖5 LSTM模型建模結果(a)與估計驗證結果(b)Fig.5 Modeling results (a)and estimation verification results (b)of LSTM model

圖5中，建模與驗證均方根誤差(RMSE)分別為1.05 N和0.72 N，最大誤差(emax)分別為5.89 N和3.97 N。

由圖5可知：LSTM力估計模型的估計結果與工業(yè)機器人氣動夾持系統(tǒng)實際夾持力輸出曲線的誤差相對較大，尤其在拐點處和峰值處，模型預測結果存在滯后性，在模型估計驗證實驗中尤為明顯。單一LSTM網(wǎng)絡面對復雜的、強非線性的數(shù)據(jù)時，無法完整獲取數(shù)據(jù)之間的長期關聯(lián)特征，造成預測結果存在滯后性，從而無法準確描述氣動夾持系統(tǒng)所存在的多值對應特性；且在訓練過程中，網(wǎng)絡的計算量會大幅度增加，訓練速度也會下降[12]。為了進一步提高LSTM夾持力模型的估計精度，文中提出了一種基于CNN-LSTM組合神經(jīng)網(wǎng)絡的夾持力估計模型。

2 基于CNN-LSTM網(wǎng)絡的夾持力估計模型

針對LSTM無法完整獲取數(shù)據(jù)關聯(lián)特征，造成模型估計誤差大的問題，利用CNN優(yōu)化LSTM網(wǎng)絡，在數(shù)據(jù)輸入LSTM網(wǎng)絡前增加一個CNN特征提取層，提取數(shù)據(jù)之間的長期關聯(lián)特征，從而優(yōu)化LSTM網(wǎng)絡，提高模型的多值對應特性的描述能力與估計精度。

2.1 卷積神經(jīng)網(wǎng)絡CNN

CNN是一種能夠進行特征提取的前饋神經(jīng)網(wǎng)絡[11]，基本結構如圖6所示。CNN的核心組成是卷積層和池化層，首先通過卷積層提取輸入信息之間的關聯(lián)特征，然后將卷積層所提取的特征傳入池化層。通過池化對數(shù)據(jù)進行降維，從而提升網(wǎng)絡訓練速度，防止過擬合。在實際應用中，一層卷積層所能提取的特征往往比較有限，為了獲得更完整的數(shù)據(jù)特征，通常將多個卷積層疊加在一起，組成多層卷積網(wǎng)絡[13]。

2.2 CNN-LSTM組合網(wǎng)絡模型

由于工業(yè)機器人氣動夾持系統(tǒng)存在復雜遲滯非線性特性，且該系統(tǒng)易受氣壓泄漏、環(huán)境等因素影響，使得影響因子之間存在復雜的耦合關系[14]。傳統(tǒng)單一的LSTM模型很難保證估計結果的準確性，而CNN能有效提取氣壓-夾持力數(shù)據(jù)中的特征信息，減少冗余輸入信息對預測結果的干擾。文中對原有的LSTM模型進行改進，將CNN與LSTM相結合，提出一種CNN-LSTM組合神經(jīng)網(wǎng)絡夾持力估計模型，其網(wǎng)絡結構如圖7所示。

由圖7可知：文中所采用的CNN-LSTM組合網(wǎng)絡結構主要由2個部分組成，第一部分是CNN特征提取層，主要由兩層卷積層構成。由于文中數(shù)據(jù)集維度較少，為減少特征提取過程中數(shù)據(jù)信息的丟失，文中所提模型中CNN特征提取層舍棄池化層，僅使用卷積層[15]。其中，每個卷積層都包含著一個ReLU激活層，具體計算如下：

Co=f(XT*Wco+bc)

(13)

式中：f(x)代表ReLU激活函數(shù)，f(x)=max{0，x}；XT為卷積層輸入向量；Co為卷積層輸出；Wco為卷積層共享權值；bc為偏置；*代表卷積操作。

數(shù)據(jù)在輸入到網(wǎng)絡模型中之前，需要先進行歸一化預處理，再運用式(13)遍歷數(shù)據(jù)集，進行數(shù)據(jù)非線性特征提取。其中兩層卷積層的卷積數(shù)量分別是16和32，卷積大小均為2×1，模型參數(shù)學習采用最速下降法完成。

經(jīng)過CNN特征提取層的數(shù)據(jù)經(jīng)展平層調(diào)整維度后傳至LSTM層，再使用式(1)—(8)建立夾持力估計模型，最后通過全連接層傳遞給回歸層實現(xiàn)夾持力估計，從而得到最終的輸出結果。

3 CNN-LSTM夾持力估計模型驗證與分析

3.1 數(shù)據(jù)采集與處理

為了更準確和全面地描述氣壓-夾持力之間的關系，文中搭建了由GP7輕型工業(yè)機器人搭載電氣比例閥(ITV3050-012BL)、氣爪(Sqeldt_MHZ2-40D)、氣泵、薄膜力傳感器(FlexiForce-A301)、樹莓派等構成的實時采集數(shù)據(jù)的實驗平臺。實驗中通過計算機控制機器人帶動氣爪進行夾持工作，并控制氣壓進行往復運動，實時采集記錄運動過程中的氣壓-夾持力實驗數(shù)據(jù)。

由于氣動系統(tǒng)易受環(huán)境干擾，為進一步逼近實際工作情況，在夾持力數(shù)據(jù)中添加隨機干擾信號，幅值取采樣值最大值的1%，以此檢驗模型的抗干擾能力。另外為檢驗所建立模型的有效性，將氣壓-夾持力數(shù)據(jù)集按4∶1劃分訓練集與測試集；并通過打亂樣本順序的方法防止出現(xiàn)有規(guī)律的數(shù)據(jù)，以避免出現(xiàn)過擬合。另外，在數(shù)據(jù)輸入到模型中進行訓練之前，需先對數(shù)據(jù)進行歸一化預處理，加快收斂速度。

3.2 模型參數(shù)設置

考慮到模型隱含層數(shù)和神經(jīng)元個數(shù)對于模型的估計精度存在較大影響，為了獲取較為精準的模型參數(shù)，文中通過實驗測試的方法，確定隱含層數(shù)及其神經(jīng)元個數(shù)，將隱含層數(shù)依次設為1和2，神經(jīng)元個數(shù)依次設為16、32、48，實驗結果如表1所示。

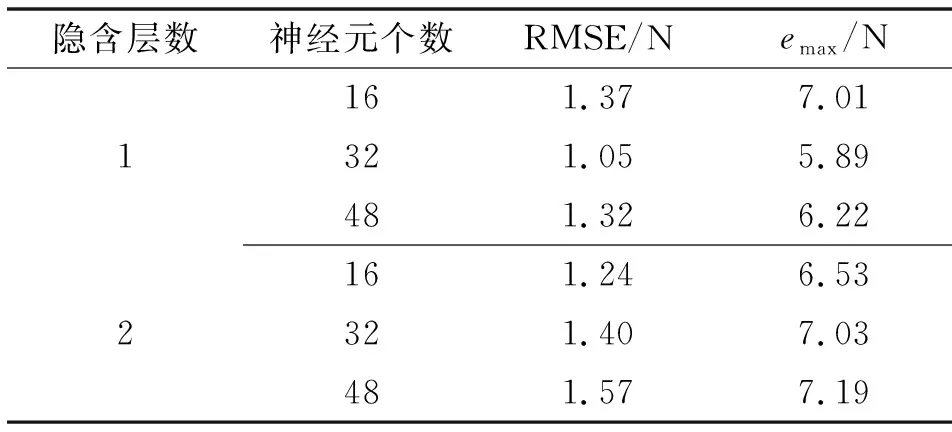
表1 不同模型參數(shù)估計結果誤差對比Tab.1 Estimation results error comparison of different model

由表1可知：當LSTM模型第一層LSTM單元個數(shù)為32時，估計誤差最小，RMSE和emax分別為1.05和5.89 N。故將第一層LSTM單元個數(shù)固定為32，再將第二層中的LSTM單元個數(shù)依次設置為16、32、48。由實驗結果得出，LSTM模型隱藏層設置為一層、LSTM單元為32個時，模型估計誤差均低于有二層隱含層時的估計誤差。故文中的LSTM模型隱含層設為1層，其中LSTM單元個數(shù)為32個。

3.3 CNN-LSTM模型有效性驗證

為了更好地驗證CNN-LSTM組合神經(jīng)網(wǎng)絡無傳感器夾持力估計模型的有效性，將它與LSTM模型進行比較分析。

圖8所示為LSTM模型的建模結果和估計驗證結果及誤差，其中RMSE分別為1.05 N和0.72 N，emax分別為5.89 N和3.97 N。由圖8可知：LSTM力估計模型的估計結果與實際氣壓-夾持力輸出曲線的誤差相對較大，估計結果存在滯后現(xiàn)象，尤其在開始處、拐點和峰值3處位置。

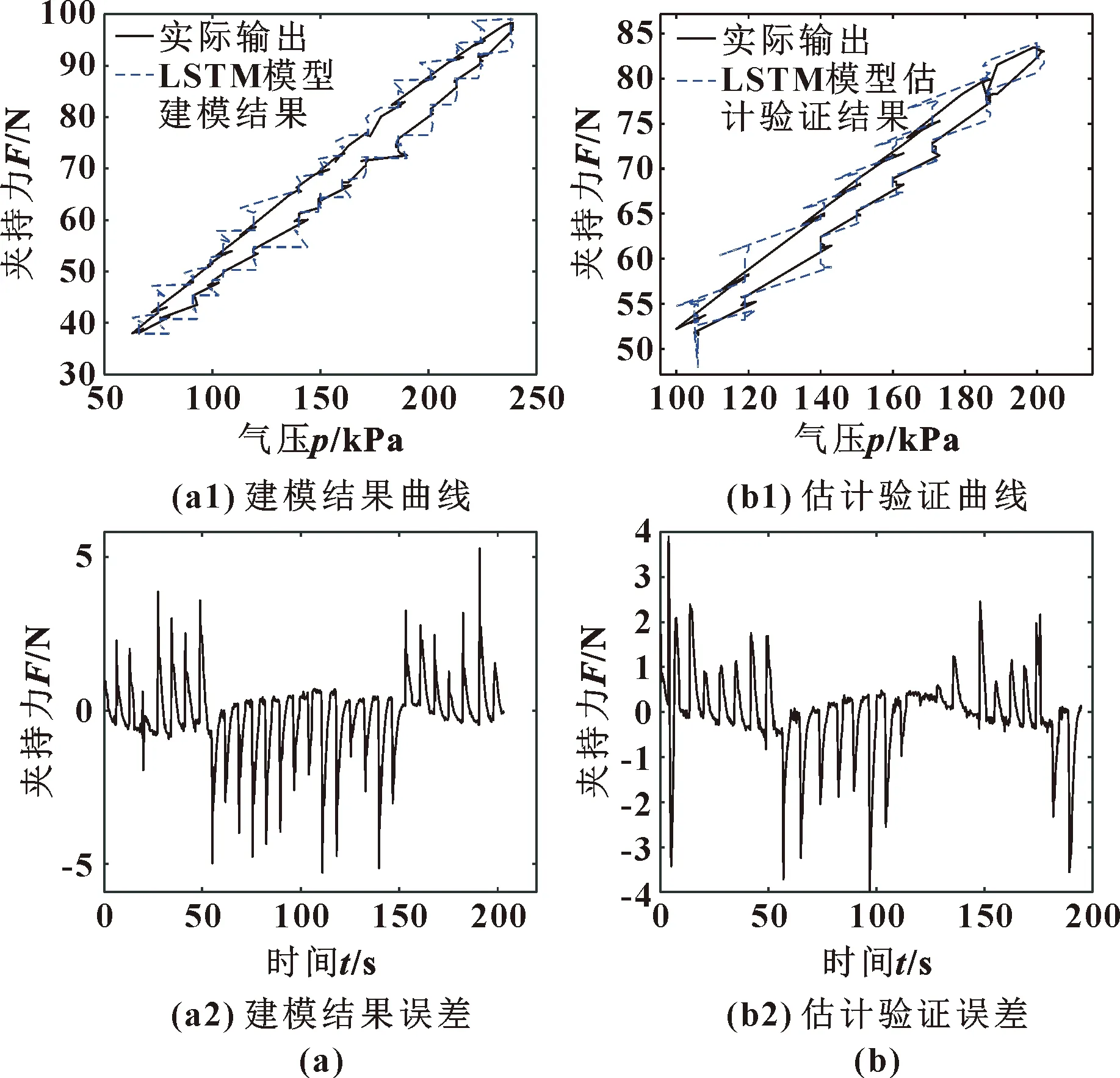
圖8 LSTM模型建模結果(a)與估計驗證(b)Fig.8 Modeling results (a)and estimation verification results(b)of LSTM model

氣爪夾持力受氣壓輸入信號、摩擦、氣壓泄漏、環(huán)境等眾多因子影響而波動較大，單一網(wǎng)絡模型估計結果誤差較大且存在滯后，圖8(b)估計驗證實驗結果中更為明顯。

圖9所示為CNN-LSTM模型的建模和估計驗證結果及誤差。其中RMSE分別為0.24 N和0.21 N，emax分別為1.19 N和0.84 N。模型所估計的夾持力輸出值和實際夾持力基本擬合，在峰值和拐點處估計值與實際值也基本吻合。

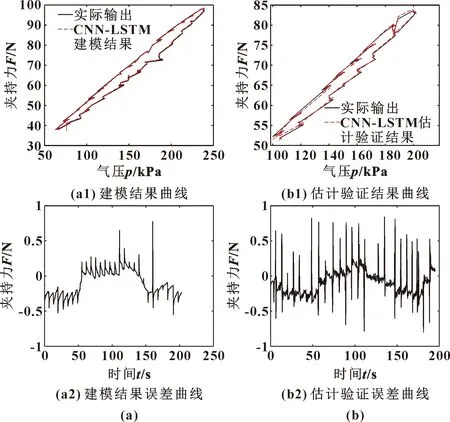
圖9 CNN-LSTM模型的建模結果(a)與估計驗證(b)Fig.9 Modeling results(a)and estimation verification results (b)of CNN-LSTM model

由圖10和圖11可知：相較LSTM建模估計方法，基于CNN-LSTM模型的建模估計方法更好，估計值也最貼近實際值。各模型夾持力估計結果的建模和估計驗證誤差對比結果如表2所示。

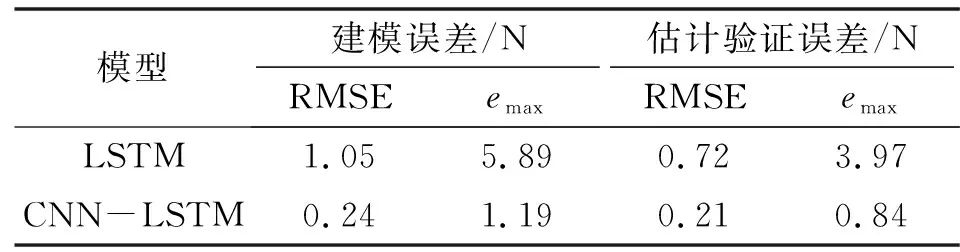
表2 不同模型估計方法誤差對比Tab.2 The error comparison of different model estimation method

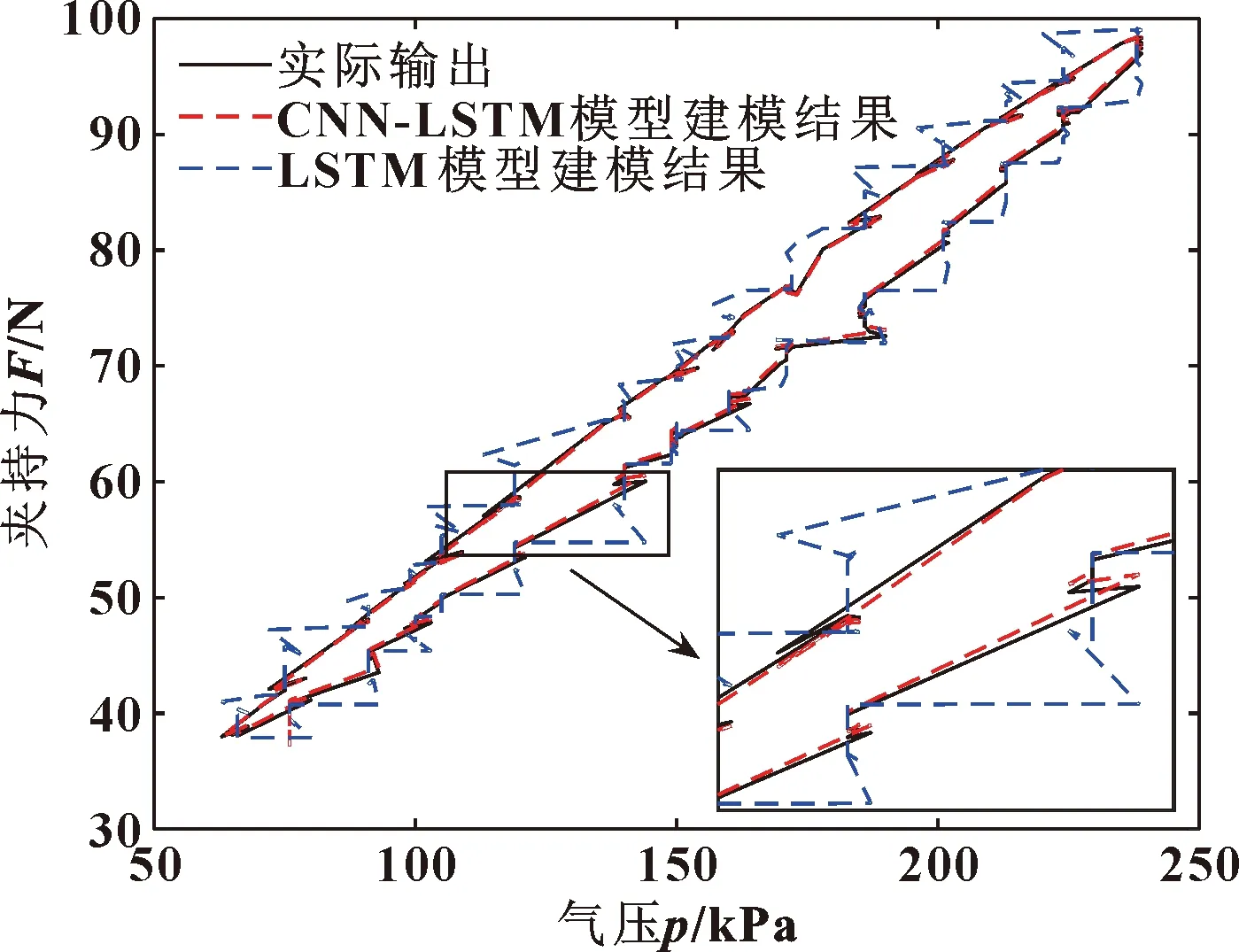
圖10 各模型建模結果對比Fig.10 Comparison of modeling results of each model

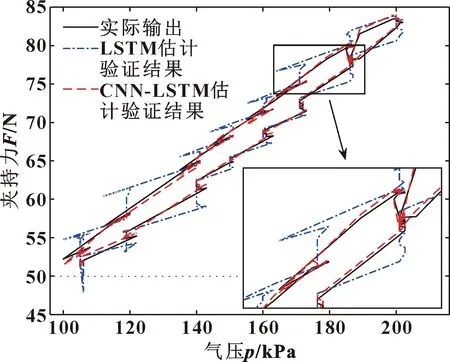
圖11 各模型估計驗證結果對比Fig.11 Comparison of estimation verification results for each model

由表2可知：基于CNN-LSTM模型建模估計方法的RMSE和emax均優(yōu)于傳統(tǒng)LSTM估計方法。通過比較分析得出，文中提出的CNN-LSTM模型的夾持力估計效果相比于其他模型具有更高的精度，其中建模與驗證RMSE分別降低了77.14%、70.83%；emax分別降低79.80%、78.84%。

4 結論

針對工業(yè)機器人氣動末端無法直接依據(jù)氣壓信號實現(xiàn)夾持力高精度控制的問題，且考慮到氣動系統(tǒng)表現(xiàn)出的遲滯、強非線性特性，與夾持力輸出所存在的多值對應特性，提出一種基于CNN-LSTM的無力傳感器低成本夾持力建模估計方法。引入CNN特征提取層，利用CNN優(yōu)化LSTM網(wǎng)絡，解決傳統(tǒng)LSTM模型無法完整獲取數(shù)據(jù)關聯(lián)特征的問題；結合CNN特征提取和LSTM非線性映射的不同功能，構建了CNN-LSTM網(wǎng)絡模型。實驗驗證結果表明：與LSTM建模估計方法相比，基于CNN-LSTM模型的建模估計方法的RMSE及emax均有降低，精度更高。該方法穩(wěn)定可靠且成本低廉，具有實際應用價值，適用于工業(yè)機器人氣動末端夾持力估計問題，為實現(xiàn)高精度夾持控制提供基礎。