一種新型六自由度并聯機器人設計

陳飛，陳機林，候遠龍

(南京理工大學機械工程學院，江蘇南京 210094)

0 前言

隨著并聯機構的誕生，各種適應不同應用場合的并聯機構層出不窮，但由于并聯機構的某些特性，如工作空間和運動速度限制了其應用范圍[1]。且常見并聯機器人結構所用傳動機構難以小型化，造成了并聯機器人結構較大，空間利用率不足。本文作者設計了一種Z軸旋轉運動不受限制的六自由度并聯機器人。相對于常見的并聯機器人，此并聯機器人不需要齒輪傳動，結構相對小巧，空間利用率較高。

文中除了介紹了這種并聯機器人的結構以及運動原理，還對此并聯機器人姿態位置的反解、受力情況以及運動所需的力矩和功率做了研究，為實際設計提供了理論依據。

1 并聯機器人結構以及運動原理

1.1 Stewart并聯機器人

1965年，英國人STEWART第一次提出六自由度的并聯機構[2]，為了達到飛行員訓練的目的，將其用作飛行模擬器。圖1所示為一個經典的六自由度Stewart機械平臺，它由6根獨立伸縮的連桿將靜平臺和動平臺連接，通過每個連桿不同的伸縮量使得動平臺可以完成6個自由度的位置和姿態變化[3]，即在空間內可作任意方向平移以及繞任意方向的轉動。

圖1 并聯機器人模型Fig.1 Parallel robot model

但這種并聯機構結構相對復雜、整體尺寸較大，工作空間一般較小。

1.2 基于軸向電機的多轉子六自由度并聯機器人

為了擴大并聯機器人的工作空間，減少整體尺寸，本文作者設計了一種新型并聯機器人，如圖2所示。此并聯機器人由靜平臺、動平臺、6個連桿、6個滑塊以及12個球鉸組成。其中靜平臺旋轉布置多個線圈，滑塊上貼有釹鐵硼磁鐵，通過不同線圈的通斷控制滑塊移動，可以將靜平臺視為定子，每個滑塊視為轉子共同組成其驅動部分。

圖2 并聯機器人模型Fig.2 Parallel robot model

此并聯機器人的動平臺位姿由6個滑臺的旋轉位置所決定，并且當滑臺之間相對位置不變時同時增加驅動扭矩可以控制此六軸機器人繞靜平臺旋轉。

2 機器人位姿反解

2.1 六自由度平臺結構參數與坐標系建立

并聯機器人模型如圖2所示，該模型動平面由6個連桿與滑臺連接。為了描述平臺的運動，將該并聯機器人抽象為一個空間幾何模型，如圖3所示。其中點1-6和7-12分別為靜平臺與動平臺球鉸的中心。

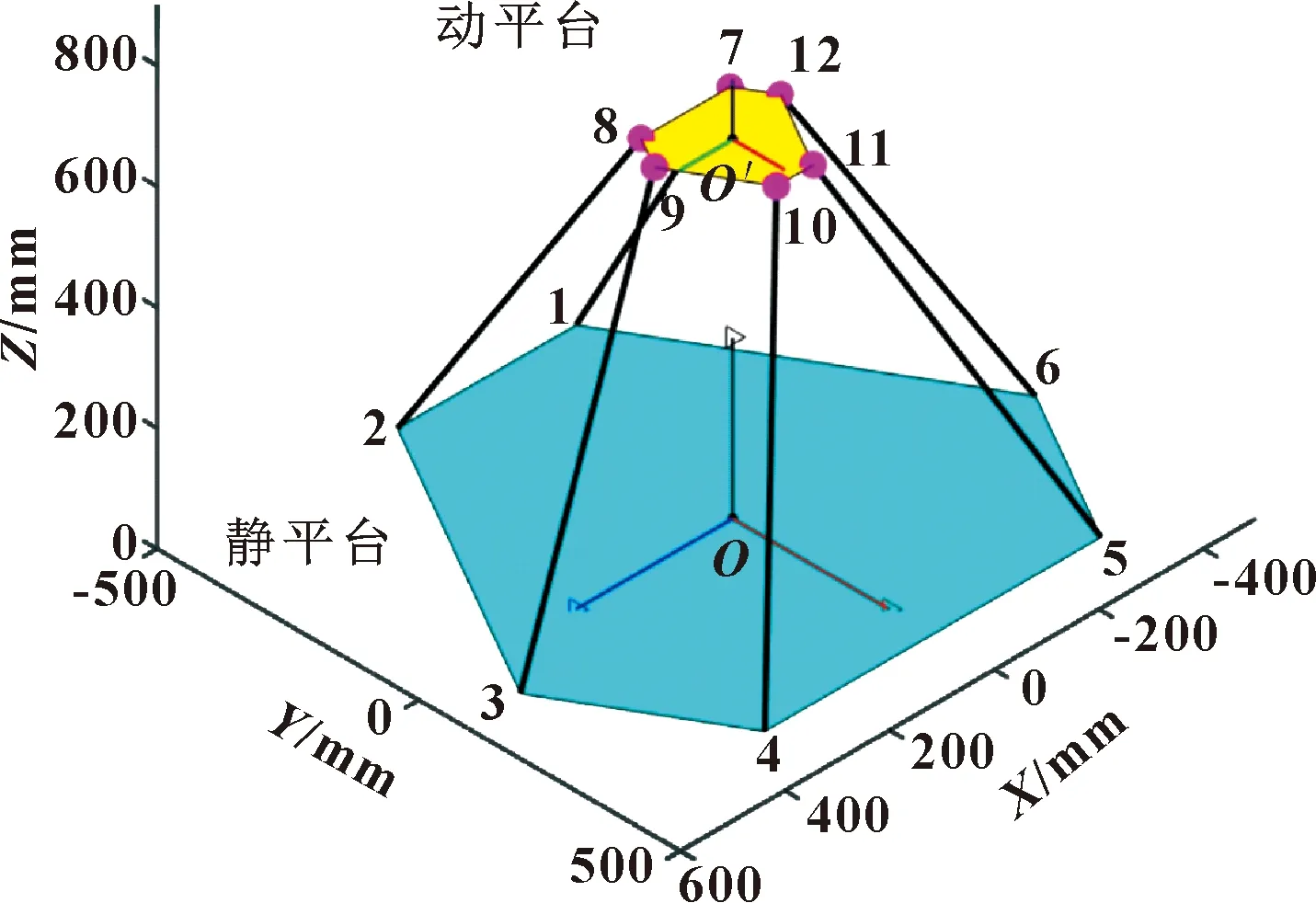
圖3 空間幾何模型Fig.3 Spatial geometry model

在平臺中心構建兩個坐標系，靜坐標系OXYZ和動坐標系O′X′Y′Z′，如圖3所示。其中動坐標系與動平臺固聯，其坐標原點位于動平臺中心，X′Y′平面與動平臺重合；靜坐標系固定在大地上，坐標原點在靜平臺中心。在平臺處于中位時，靜坐標系與動坐標系平行，當動平臺運動時，動坐標系隨平臺一起運動，而靜坐標系始終靜止不動。

定義并聯機器人結構參數如表1所示。

表1 并聯機器人尺寸參數Tab.1 Dimension parameters of parallel robot

2.2 運動學反解

運動學反解是在已知末端執行器的位置和姿態的情況下求解驅動器的運動量[4]。文中末端執行器為動平臺，驅動器是6個滑臺，可通過動平臺位姿信息求解各滑臺與X軸的夾角θ。

當動平臺具有位姿Q=(αβγXYZ)時可以得到動平臺繞動坐標系的旋轉變換矩陣如下：

(1)

(2)

(3)

(4)

(5)

式中：RX(α)、RY(β)、RZ(γ)分別表示動平臺繞靜平臺X、Y、Z軸旋轉的旋轉矩陣，以順時針為正；P0為動平臺相對靜平臺的位移；T為動坐標系到靜坐標系的坐標變換矩陣。

對任意某支鏈分析，定義其連接動平臺的球鉸中心為點A，連接滑塊球鉸中心為點B，如圖4所示。

可得OA=TO′A+P0

(6)

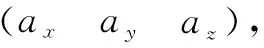
(7)

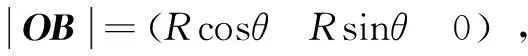
cosφ=ax·Rcosθ+ay·Rsinθ=

(8)

定義：

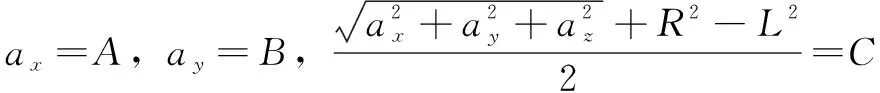
(9)

可知滑塊i與X軸夾角θi，實際解算后θi有兩解，即表示對于動平臺的某一固定位姿Q，每個滑塊有兩個位置可以滿足運動需求，實際運動中將造成滑塊位置沖突，如圖5所示。

圖5 滑塊位置沖突Fig.5 Slider position conflict

位置沖突會導致滑塊相撞，可通過滑塊之間相對位置避免。具體步驟為：由滑塊大小可得兩滑塊互補相撞的最小夾角θmin，計算相鄰兩滑塊之間角度差使其大于最小夾角θmin。滑塊夾角示意如圖6所示。

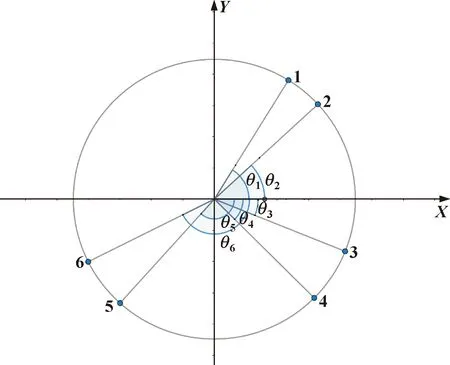
圖6 滑塊夾角示意Fig.6 The angle between the sliders

3 并聯機器人應力分析

并聯機器人的動力學研究方法有：牛頓-歐拉(Newton-Euler)方程、達朗伯原理-虛位移原理、拉格朗日(Lagrange)方程、高斯(Gauss)方法、凱恩(Kane)方法、螺旋理論等[5]。文中采用牛頓-歐拉方程求解，分析此并聯機器人位姿Q的應力。

當動平臺具有位姿Q=(αβγXYZ)時，由于此并聯機器人的連桿為輕量化鋁合金，為簡化計算可將忽略其重力參數，視為二力桿。則定義以下參數便于計算，見表2。

表2 并聯機器人運動參數Tab.2 Kinematic parameters of parallel robot

3.1 支鏈受力分析

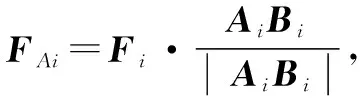
3.2 滑塊力分析

滑塊視為一個剛體，其受支鏈的反作用力、底座向上的支持力和指向坐標原點的法向力、線圈繞組對滑塊的拖拽力。其中滑塊切向力僅只有線圈繞組切向的拖拽力、慣性力的切向分量與支鏈反作用力的切向分量。則有：

(10)

其中：Ti為線圈繞組的拖拽力切向分力。

3.3 動平臺受力分析

動平臺受6個支鏈的反作用力與動平臺自身重力G，在動平臺運動時還有慣性力與慣性力矩，其合力與合力矩為0。

在靜坐標系下，動平臺重力G、慣性力與6個支鏈的反作用力合力為0：

(11)

在動平臺質心處，支鏈的反作用力矩、重力力矩以及慣性力矩滿足

(12)

公式(11)(12)在靜坐標系下可以分為X、Y、Z三軸的分量解算，得到一個6個未知數的方程組。

4 多轉子結構

此并聯機器人的驅動部分可以使用齒輪組合的方式通過固定在滑臺的電機驅動小齒輪轉動移動滑塊，但齒輪組合的方式需要在滑臺固定電機，增加了并聯機器人的尺寸大小，且動平臺繞Z軸旋轉圈數增加時電機的電纜線會互相纏繞。為避免這種情況，本文作者設計了一種軸向電機的多轉子驅動結構。

4.1 多轉子結構

此并聯機器人的底座與滑臺結構，由類似軸向電機的方式組成[6-7]，如圖7、8所示。

其底座含有多個線圈繞組，每個線圈繞組可單獨通斷。滑臺含多個釹鐵硼磁鐵結構，在相近繞組接通后給予其動力，使得滑臺在底座轉動。通過控制相鄰線圈繞組通過的電壓大小可以使水平方向的拖拽力與滑臺運動軌跡相切，其控制方式類似無刷電機FOC(Field-Oriented Control)控制[8]。此驅動方式的并聯機器人活動結構無電線連接，避免了運動過程中電纜的限制，同時其線圈繞組內置在底座上，滑臺上僅需貼上釹鐵硼磁鐵即可，大大減小其結構尺寸。

4.2 驅動扭矩與功率分析

滑臺受力分為3個部分：支持力、軸向拉力以及切向力。其中切向力由線圈繞組提供。其驅動扭矩最大值由切向力決定，功率由滑塊運動速度與切向力共同決定。

4.3 轉子轉矩加強方法

轉子可提供的轉矩決定了此并聯機器人運動的快慢，要加強轉子力矩除了增加線圈繞組通過的電流還可以通過如下兩種方法：(1)增加滑臺尺寸，增加其釹鐵硼磁鐵的對數。(2)改變釹鐵硼磁鐵的排列結構，將單個釹鐵硼磁鐵變為多個小的釹鐵硼磁鐵組成的強磁陣列[9]的結構，如圖9所示。

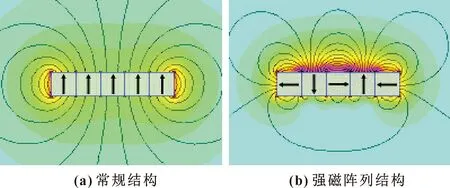
圖9 釹鐵硼磁鐵的排列結構Fig.9 The arrangement structure of NdFeB magnet：(a) conventional structure；(b)strong magnetic array structure

5 結論

常規的六自由度并聯機器人空間運動范圍有限，本文作者提出一種新型并聯機器人，具有Z軸轉動不受限制的特點，極大地擴展了其運動范圍；且此并聯機器人驅動部分僅有線圈和釹鐵硼磁鐵組合，可以視為一個拆解的軸向電機，避免了齒輪傳動結構，還具有軸向電機結構尺寸小、動力大等優點；相對常規并聯機器人結構尺寸極大減少，對并聯機器人的設計有一定的啟發作用。本文作者還提供了此并聯機器人運動姿態反解、運動受力分析，以及驅動器設計所需的幾個重要參數來源，便于實際設計。