基于運算本質一致性的結構化教學探索
——《分數四則混合運算》教學
文|李柱俊
【教學內容】
蘇教版六年級上冊第75 頁例1 和“練一練”,第76 頁的第1~5 題。
【教學過程】
一、自覺提問,嘗試計算
師:同學們,看到課題,你們想問什么?
生:什么是分數四則混合運算?(板書:是什么?)
生:分數四則混合運算怎么算?(板書:怎么算?)
生:它和整數、小數四則混合運算有聯系嗎?(板書:聯系?)
師:會提問也一定愛思考,我們首先看看第一個問題:什么是分數四則混合運算?誰可以舉例說明?
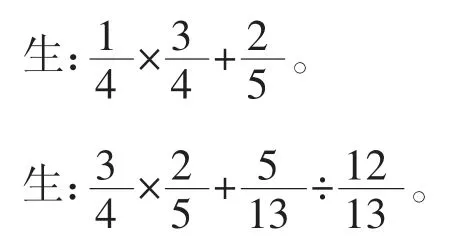
(教師巡視,收集按運算順序做和運用乘法分配律簡便計算的兩種不同作品)
【設計意圖:結合學生的學習心向,開門見山讓學生根據課題提出問題,培養學生問題建構力的同時,也激發了學生學習的熱情。】
二、自主研究,理解算理
1.多元計算,理法相融。
(1)小組探究
師:我們先來看看這位同學的計算(如下圖),他是按怎樣的順序計算的?
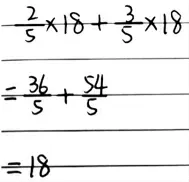
師:你們的得數和他一樣嗎?
師:先算乘法,再算加法,到底合不合理?(板書:運算順序合理?)
師:數學是講道理的學科,你能想辦法證明嗎?以小組為單位,每個小組至少選擇兩種驗證方法。有困難的可以看看研究小貼士。

【設計意圖:運算順序的合理性是分數四則混合運算的核心要素之一,從問題出發,逆向而行,引領學生探究算法和算理之間的關系,指向的是在學習過程中運算能力這一核心素養的落實。】
(2)算理交流
●方法一:轉化成小數
師:這是誰的研究成果?(如下圖)說說你是怎樣想的。
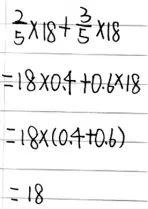
小結:將分數改寫成了小數,得到相同的結果,證明了先算乘法的合理性。(板書:分數、小數)
●方法二:編題法
師:(如下圖)這是通過編題來證明的,你能根據他編的題目說說為什么可以先算乘法嗎?

小結:借助解題思路分析了先算乘法的合理性。
●方法三:把分數量轉化成整數量
師:你能看懂這幅作品的想法嗎?(如下圖)

生:他是把分數表示的量用整數來表示,再進行計算的。(板書:整數)
●方法四:畫圖法
師:能看懂別人的做法是會學習的表現。這還有一位同學是畫圖解釋的。(如下圖)
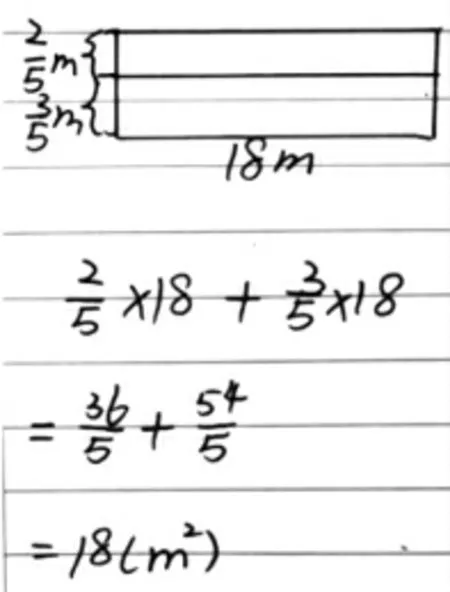
師:從他的圖中你明白了為什么可以先算乘法嗎?
2.引導比較,歸納算法。
師:觀察幾種不同的驗證方法,都證明了什么?
師:看來按照這樣的順序計算是合理的(擦去合理后面的問號),這個運算順序我們熟悉嗎?
生:其實就和整數、小數的混合運算順序是一樣的。
小結:分數四則混合運算的運算順序和整數、小數四則混合運算的運算順序都是一樣的。(板書:運算順序一致)
【設計意圖:運算順序的一致性是分數四則混合運算的另一個核心要素,在對運算順序合理性的詢證過程中,學生感悟到其實分數四則混合運算的運算順序是與整數、小數的混合運算順序一致的。】
三、聯通算理,優化算法
師:老師巡視的過程中,發現有同學是這樣做的(如下圖),猜一猜,他是怎么想的?

生:他運用乘法分配律進行了簡便計算。
師:乘法分配律在分數混合運算中適不適用?你能不能結合編的題目解釋算的是什么?
師:還有不同的嗎?
師:誰還能結合這幅圖來說說?
師:這幾位同學結合解題思路都說清楚了先算括號里的加法也是合理的。是在做同一件事情,它們之間是相等的關系。18 可以變化成證明了什么?
生:乘法分配律也可以用在分數中。
師:原來,整數的運算律對于分數同樣適用。(板書:運算律適用)如果是你,你會選擇哪一種來計算?為什么?
生:第二種,因為更簡便。
師:是的,在這里數字就是這么巧合,有時運用運算律可以使計算更簡便。(板書:簡便)
回顧:回頭看看大家之前提出的問題,你現在知道怎樣計算分數四則混合運算嗎?
追問:分數、小數、整數四則混合運算之間有什么聯系?
小結:分數、小數、整數四則混合運算的運算順序都是一致的,運算律也適用于分數四則混合運算。
提問:課的開始同學們列舉的兩道分數四則混合運算,說一說分別是按照什么運算順序計算的。
【設計意圖:讓學生對自己和他人的問題解決過程給出合理解釋,提供不完全歸納發現運算律對于分數四則混合運算也同樣適用,有助于學生養成講道理、有條理的思維習慣,發展學生的推理意識和能力。】
四、鞏固練習,強化規則
1.能簡算的要簡算。
(1)獨立完成。
(2)核對、反饋。
(3)追問:明明是先算除法的,為什么轉化成乘倒數后就一起算了呢?
(4)強調:在計算分數四則混合運算時,有時要邊算邊看能不能簡便。
2. 在下面各數中間添上運算符號或括號,并計算出得數。
(1)說說你是怎么想的。
(2)追問:幾道算式四個數都相同,為什么結果不同?
3.在下面各數中間添上運算符號或括號,使等式成立。
【設計意圖:結合運算能力和推理意識的能力素養表現,基于分數四則混合運算的兩大核心要素,設計了三道整體性、進階性的習題,習題1 是基礎題,習題2 是標準題,習題3 是挑戰題。潛能生可不做挑戰題,優等生可不做基礎題,所有學生都要做標準題。】

