基于循環(huán)前綴的線性調(diào)頻信號抗干擾探測波形設計方法
占郁雯,張?zhí)熨t,王舒玉
(電子科技大學 信息與通信工程學院, 四川 成都 611731)
0 引 言
隨著雷達應用場景日益復雜,雷達干擾技術不斷更新和變革,雷達抗干擾技術的研究刻不容緩。自雷達誕生之日起,大部分關于抗干擾和噪聲抑制的研究都是針對后端的信號處理方法展開的,最典型的即為窗函數(shù)法[1],然而其實質(zhì)上是對雷達信號進行失配處理,無可避免地帶來主瓣展寬和回波信噪比損失,導致雷達分辨率下降和探測性能惡化。另一種方法是基于發(fā)射波形設計的角度,通過對發(fā)射波形進行有針對性的優(yōu)化設計實現(xiàn)干擾抑制。在波形設計中,抑制干擾和噪聲的思路主要有兩種:通過設計波形的自相關來抑制距離單元內(nèi)來自其他距離單元的距離旁瓣干擾和通過設計波形功率譜來抑制干擾[2]。從公開發(fā)表的文獻看,目前基于發(fā)射波形設計的干擾抑制算法主要可以分為以下兩類:第一類是通過約束發(fā)射波形自身的自相關函數(shù)旁瓣特性[3-10];第二類是通過學習電磁環(huán)境中的有利因素并利用有用信息實時的對雷達發(fā)射波形進行有針對性的設計,在目標特性或雷達探測背景參數(shù)變化時,自適應的優(yōu)化調(diào)整發(fā)射波形[11-17]。但如今,波形設計的研究主要著力于發(fā)射波形的優(yōu)化上,在雷達接收端依然沿用傳統(tǒng)的匹配濾波技術,因而無法擺脫距離旁瓣或者自相關函數(shù)旁瓣產(chǎn)生的干擾的影響。
線性調(diào)頻(LFM)是現(xiàn)代高性能雷達系統(tǒng)中常用的信號波形之一。它具有較大的時間時寬帶寬積,其相位譜具有平方律特性,因此在脈沖壓縮過程中可以得到較大的脈沖壓縮比。同時,LFM信號在使用的匹配濾波器進行脈沖壓縮后,其對多普勒頻移表現(xiàn)不敏感[18-19]。正交頻分復用(OFDM)多載波信號由于其具有通信速率高、抗干擾性能強等特性被選用為4G和5G通信載波信號[20]。在現(xiàn)代通信系統(tǒng)中,通過在OFDM傳輸波形中添加足夠長的循環(huán)前綴(CP),可以實現(xiàn)從碼間干擾信道到無碼間干擾子信道的轉換,從而有效地抑制了多徑干擾。文獻[[21]將OFDM信號用于雷達目標探測,提出一種類似逆濾波的算法,其歸一化目標點擴展函數(shù)結果表明,相比于LFM,加循環(huán)前綴的OFDM信號可以實現(xiàn)更低的距離旁瓣脈壓效果,而且主瓣并未展寬。綜上所述,基于波形設計的抗干擾探測波形設計以及信號處理方式在應對當今復雜多變的干擾環(huán)境時是頗具成效的。隨著雷達系統(tǒng)不斷更新發(fā)展以及硬件技術不斷變革創(chuàng)新,在實際工程中波形設計技術有著巨大的應用潛力與研究前景。因此,亟需開展新一代的抗干擾探測波形設計理論與處理方法的研究,提高雷達的抗干擾性能。
本文提出了基于CP的LFM雷達波形設計與優(yōu)化處理方法。該方法建立干擾波形和抗干擾探測波形的發(fā)射、接收信號數(shù)學模型,利用基于CP的脈沖壓縮算法實現(xiàn)目標距離向的估計,通過包絡約束-共軛梯度算法獲取近似解。仿真實驗驗證了本文所提方法的可行性和有效性。
1 信號發(fā)射與接收模型
1.1 信號發(fā)射模型
一個典型的抗干擾探測系統(tǒng)如圖1所示。機載一體化系統(tǒng)發(fā)射抗干擾探測信號并接收目標反射的雷達回波信號,同時干擾機截獲我方發(fā)射信號并轉發(fā)干擾信號至雷達系統(tǒng)的接收端。
如圖2所示,取LFM信號的末尾部分(t∈[T,T+TCP)為信號的循環(huán)前綴,并將該循環(huán)前綴添加至上述LFM信號的開端部分,得到抗干擾探測信號(CP-LFM)的數(shù)學模型
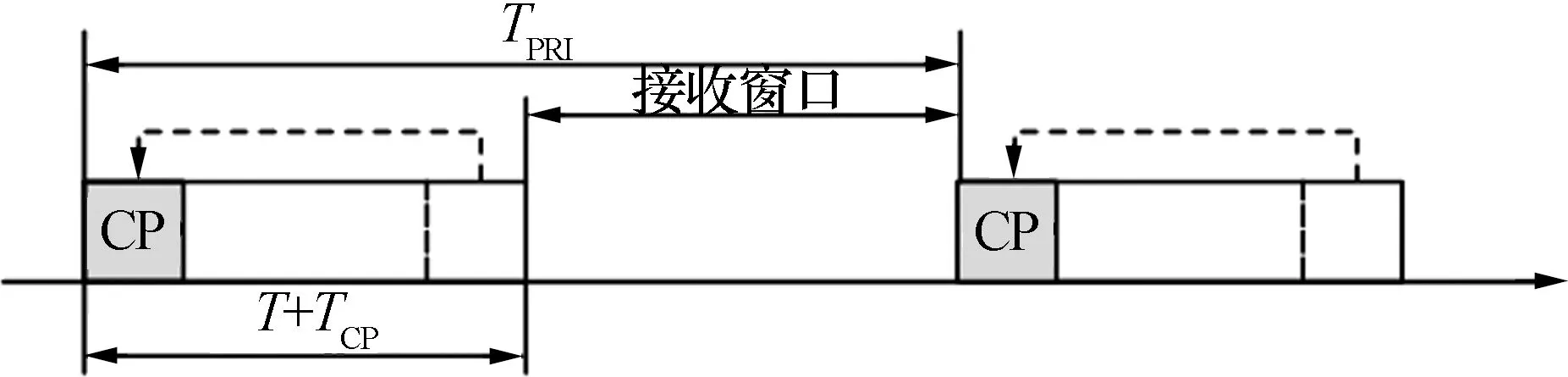
圖2 CP-LFM信號示意圖Fig.2 CP-LFM signal schematic diagram
(1)
式中:T為LFM信號脈寬(不包括循環(huán)前綴);K=B/T,為信號調(diào)制斜率;B為信號帶寬;TCP表示循環(huán)前綴的時間長度。
1.2 干擾機干擾模型
假設干擾機截獲信號采用的干擾方式為切片轉發(fā)干擾形式,則單個切片干擾sj(t)可以表示為
(2)
式中:τ為干擾機的采樣時寬;L=τ/Ts,為干擾機截取單個切片的長度;Q為切片干擾的復制次數(shù),Q=(T+TCP)/τ。將干擾復制Q次得到切片干擾j(t)的數(shù)學模型為
(3)
1.3 信號接收模型
假設CP-LFM發(fā)射信號的帶寬為B,則其對應的雷達距離向分辨率為ρr=c/(2B)。假定雷達天線主瓣所照射到的區(qū)域沿距離向的寬度為Rw,則該區(qū)域沿距離向可以被分割為M=Rw/ρr個距離分辨單元。因此,雷達接收機收到的回波信號是M個距離分辨單元的雷達回波信號的疊加,可以表示為
(4)
式中:αm為第m個距離分辨單元加權目標反射系數(shù);Rm為第m個距離分辨單元到雷達的距離;w(t)為雷達系統(tǒng)接收機噪聲;c為光速。
以Ts為周期進行離散采樣,得到離散回波序列為
(5)
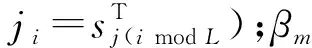
(6)
2 基于CP的LFM雷達脈沖壓縮算法
在通信應用中,要解決M條不同的多徑之間的碼間干擾的問題,循環(huán)前綴的長度至少要為M-1。同理,雷達接收機收到CP-LFM一體化信號回波序列時,首先去除首尾M-1個采樣值,并將回波序列表示成如下向量形式。
(7)
其中C表示為
(8)
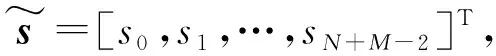
(9)
矩陣C可由向量[β0…βM-2βM-10 … 0]T進行循環(huán)移位可得下列N×N矩陣
(10)
對接收到的雷達回波解調(diào)到基帶之后,對序列進行快速傅里葉變化(FFT),于是得到
(11)

(12)
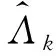
(13)
至此,雷達的脈沖壓縮已經(jīng)完成。
3 抗干擾探測聯(lián)合優(yōu)化模型
根據(jù)脈壓結果式(13)可知,第m個距離分辨單元的輸出信干噪比(SINR)表示為
(14)
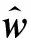
(15)
受到發(fā)射機功率限制以及波形能量的約束,進一步考慮波形的恒模約束。因此在波形矢量的恒模約束下,聯(lián)合雷達的探測性能與抗干擾性能,以輸出SINR最大為目標,建立聯(lián)合優(yōu)化模型如下
(16)
4 抗干擾探測一體化信號優(yōu)化算法
由于該優(yōu)化問題式(16)的恒模約束是非線性約束,用傳統(tǒng)的約束優(yōu)化方法在處理恒模約束時,在下降方向進行搜索時要不斷地檢驗當前點是否滿足恒模約束,較為復雜。因此,將包絡約束重構成如下表達式
sk+1=exp(jdiag(φ(sk)))1,sk∈Samp(1)
(17)
其中,Samp(v)={x∈K:‖x⊙x*-diag2(v)1‖=0},是指定幅度的向量集合,單模設計下v=1;φ:N→N表示相位。在算法保證迭代在單模約束Samp(1)下進行。
利用式(17)引入的黎曼優(yōu)化概念,提出一種包絡約束下的非線性規(guī)劃。該方法的搜索函數(shù)定義為
φ(sk)=μd+Φ(sk)1
(18)
其中Φ(·)=Im(ln(diag(·))),μ∈(0,∞)為步長,d∈N是由梯度確定的搜索方向。
將優(yōu)化模型表達式(16)轉化成為與序列s相關的目標函數(shù)
(19)
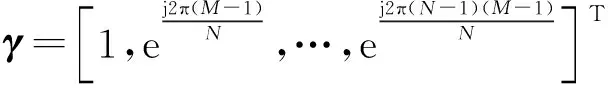
利用鏈式法則,可以得到目標函數(shù)的相位梯度為
(20)
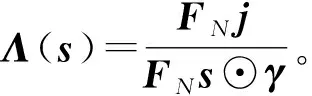
至此,包絡約束-共軛梯度算法的具體步驟如下。
1)輸入k=0,初始化信號包絡序列s0,下降方向d0=-g0=-ψO(s0),最大迭代次數(shù)Imax。
2)輸出Om的最優(yōu)值,優(yōu)化后信號序列sm。
3)重復。
(1)尋找最優(yōu)步長μ
Om(exp(jμdiag(dk))sk)≤Om(exp(jηdiag(dk))sk)
其中,?η≥0。
(2)sk+1=exp(jμdiag(dk))sk
(3) 計算新的搜索方向。
gk+1=ψO(sk+1)
(4)k←k+1
(5) 如果k (6) 結束迭代,輸出目標函數(shù)Om,優(yōu)化后信號序列sm。 為了驗證本文所提的基于CP的脈沖壓縮算法的有效性以及所設計的LFM波形的性能指標,對其進行仿真。仿真參數(shù)如表1所示。 表1 仿真參數(shù)表Tab.1 Simulation parameter table 假設干擾方采取的干擾方式為切片轉發(fā)干擾,并且干擾機截獲我方信號的長度占總信號長度的比例為10%~100%。 圖3 優(yōu)化算法收斂曲線圖Fig.3 Optimization algorithm convergence curve 如圖3所示,該算法的收斂性是可以保證的,在之后的仿真驗證實驗中,采取收斂至最優(yōu)時的波形作為本文所設計的波形進行驗證。 在分析信號的抗干擾性能時,假設干擾方采取截取-切片轉發(fā)的干擾方式,以回波信號功率與干擾信號功率(即SINR)來進行分析。如圖4所示,當干擾機截取我方信號長度小于總體信號長度時,本文所提出的波形設計方法與傳統(tǒng)LFM信號的匹配濾波相比,本文所提出的基于CP的LFM信號設計方法明顯優(yōu)于傳統(tǒng)LFM信號,可以獲得更好的抗干擾性能。 圖4 CP-LFM信號與傳統(tǒng)LFM信號SINR對比圖Fig.4 Comparison of SINR between CP-LFM signal and traditional LFM signal 為了驗證提出的基于CP的脈沖壓縮算法的有效性,假設干擾機對我方信號截取信號長度占總信號長度的60%場景下,給出了LFM波形在經(jīng)過基于CP的脈沖壓縮算法后不同距離分辨單元脈沖壓縮后的SINR(受干擾情況下的脈沖壓縮結果圖)。對比起見,以下還給出了具有相同參數(shù)(如發(fā)射信號能量、信號脈寬、信號帶寬等)、相同干擾信號下的LFM信號經(jīng)過匹配濾波后的SINR的結果,從圖5中可以看出,干擾信號的能量比傳統(tǒng)的LFM信號的脈壓結果有所降低。對于所有的距離分辨單元,所設計的基于CP的LFM信號脈沖壓縮后的SINR比傳統(tǒng)LFM信號匹配濾波后的SINR大。這是由于利用所設計的基于CP的LFM信號脈沖壓縮后不存在距離旁瓣的影響;而傳統(tǒng)的匹配濾波后卻存在旁瓣,造成距離分辨單元間的能量相互干擾,降低了脈沖壓縮后信號的SINR。 如上述仿真實驗顯示,該設計波形具有更優(yōu)的抗干擾性能。同時,為了判斷在傳統(tǒng)的雷達發(fā)射系統(tǒng)與接收系統(tǒng)下的探測性能,給出該設計波形的模糊函數(shù),如圖6所示,該波形的模糊函數(shù)接近傾斜刀刃型,具有良好的多普勒容限。 圖6 所設計信號基本特征Fig.6 The basic features of the designed signal 將本文信號與LFM信號進行對比,發(fā)現(xiàn)本文信號速度分辨率和距離分辨率與LFM相似,通過模糊函數(shù)證明了優(yōu)化后的CP-LFM信號的探測性能。 本文提出了基于循環(huán)前綴(CP)的LFM信號抗干擾探測波形設計與處理方法,并給出了信號設計流程。通過聯(lián)合雷達脈壓和干擾機的干擾處理方法,構建了抗干擾探測聯(lián)合優(yōu)化問題模型。本文提出的基于CP的LFM聯(lián)合優(yōu)化設計與處理方法與傳統(tǒng)的脈壓方法相比,在抗干擾方面能夠獲得更加優(yōu)良的性能。基于發(fā)射端與接收端聯(lián)合設計,實現(xiàn)了該一體化發(fā)射信號和處理方法的匹配。仿真結果表明,本文所提方法可以適應雷達探測的基本需求,并且使得回波信號的抗干擾性能得到了一定的提升,能夠同時保持雷達的探測和抗干擾性能。脈壓效果表明,相比于傳統(tǒng)匹配濾波算法本文脈壓算法也具有更低的旁瓣。5 仿真結果
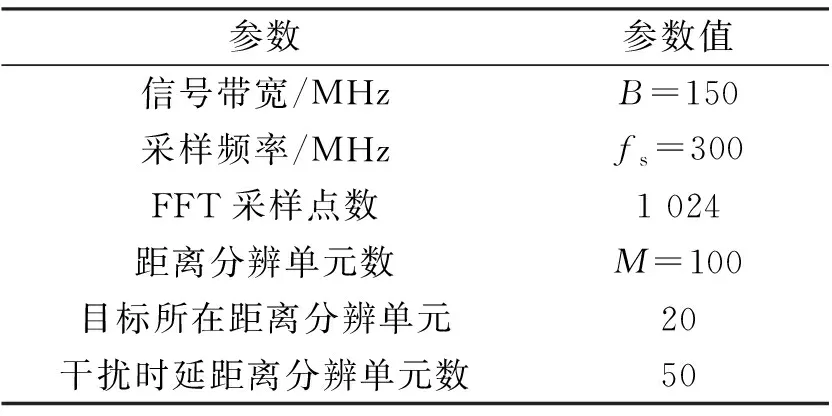
5.1 算法有效性分析
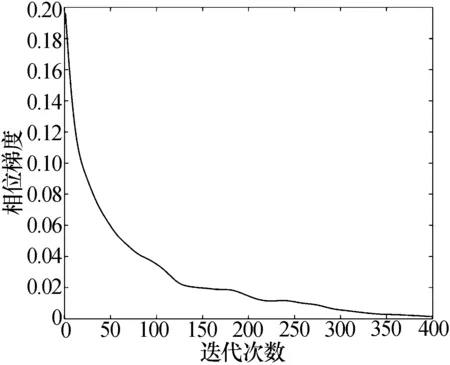
5.2 抗干擾性能分析
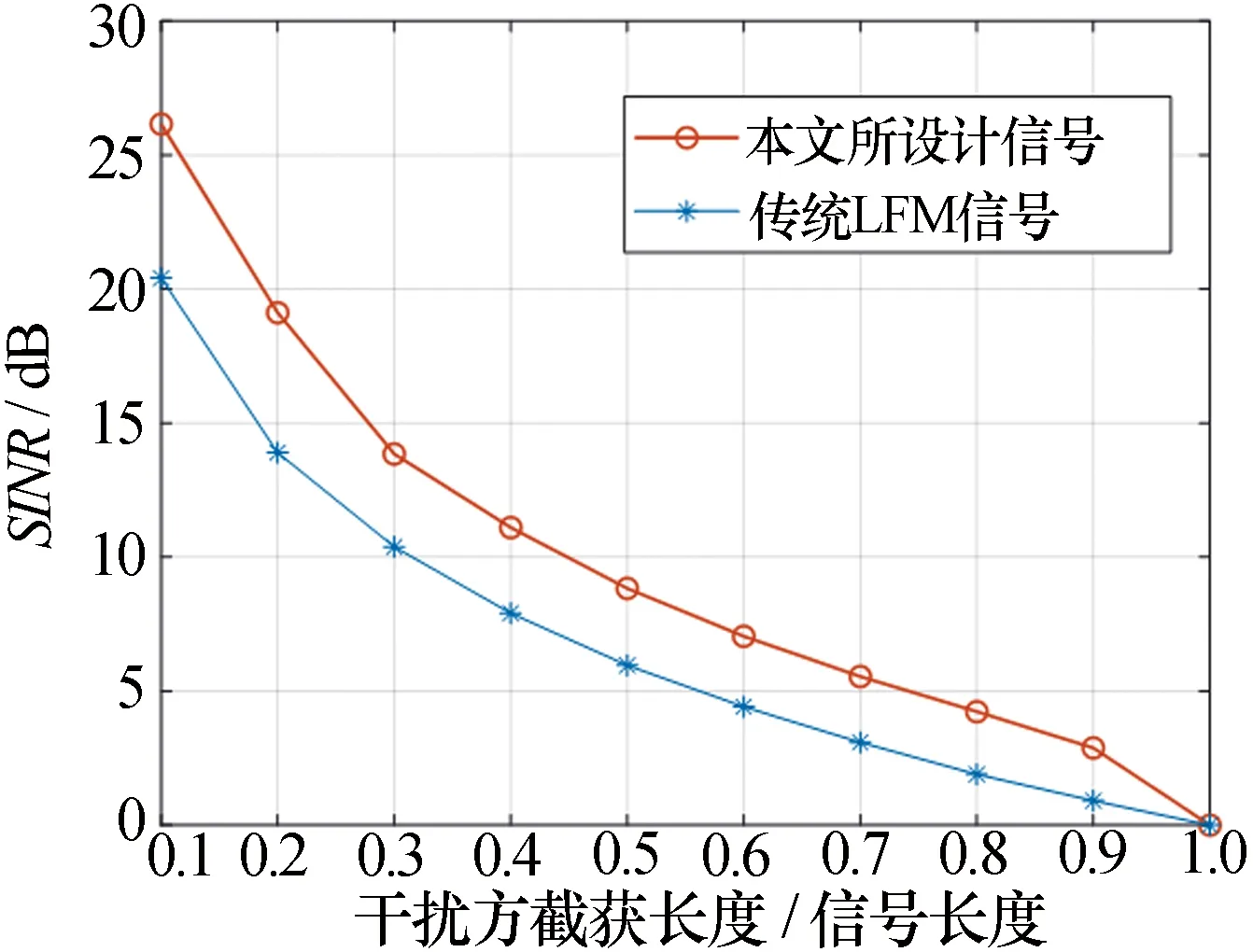
5.3 不同脈沖壓縮算法對比
5.4 探測性能分析
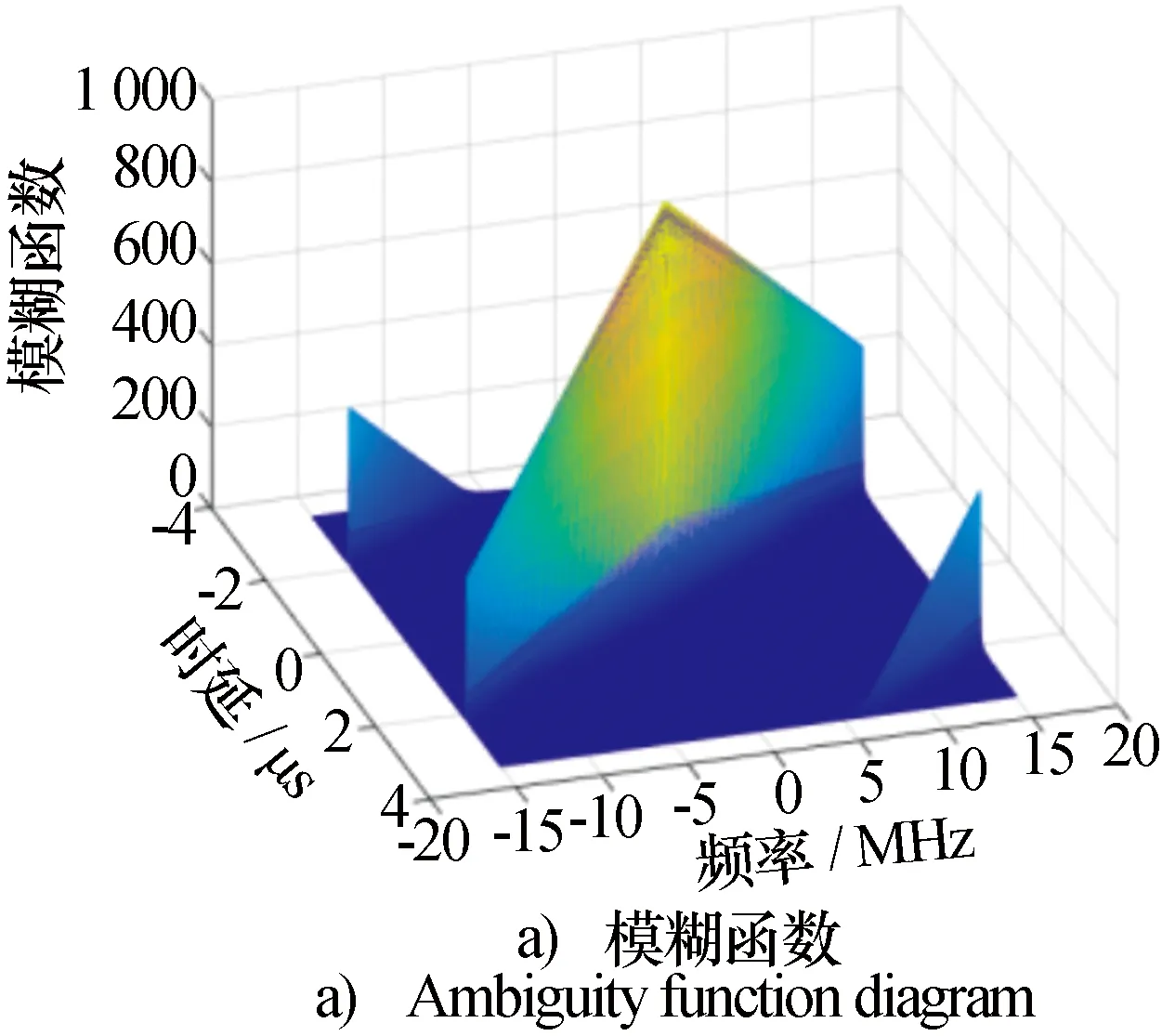
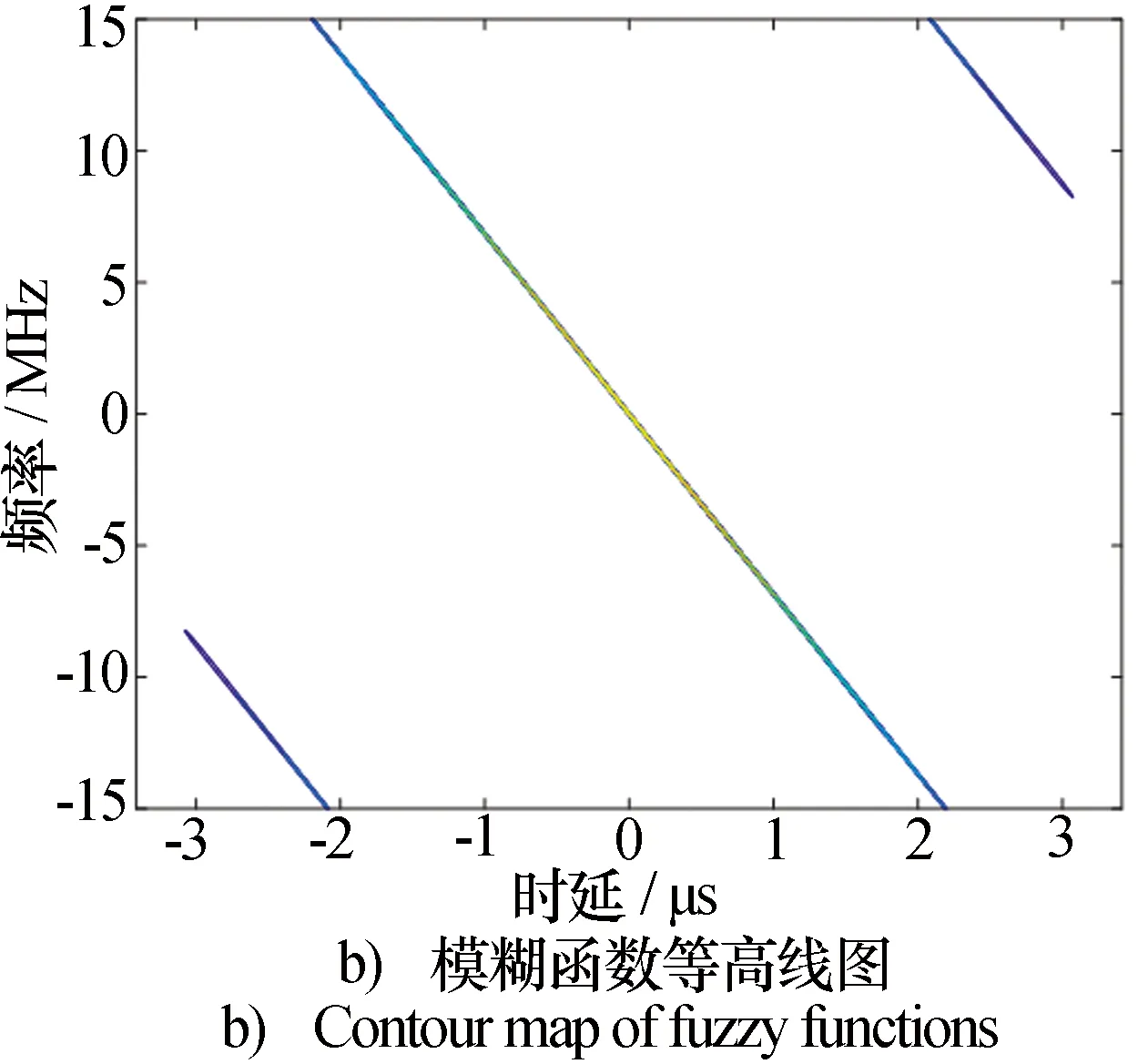
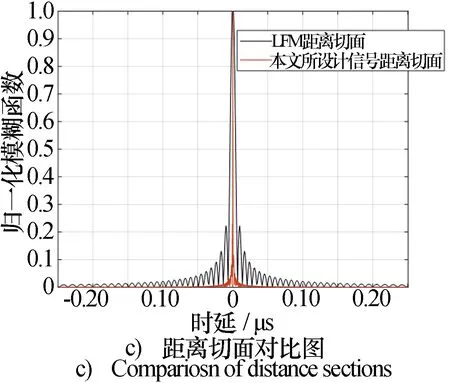
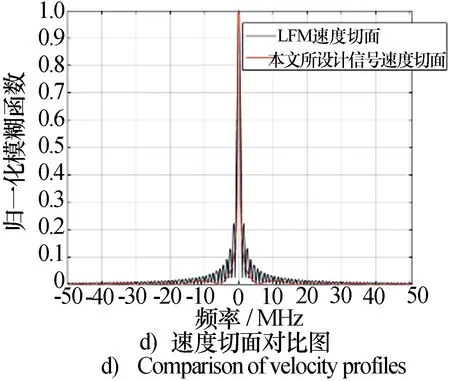
6 結束語

