基于數據驅動的高校預算管理模型及應用研究

馮振權

（作者單位：遼寧科技大學）

傳統的高校預算管理通常基于經驗和主觀判斷，缺乏科學依據和長期規劃。然而，隨著信息技術的快速發展和數據分析方法的進步，高校可以利用大數據、數據挖掘和預測建模等技術，解決預算管理中的復雜性和不確定性問題。在這樣的背景下，基于數據驅動的高校預算管理模型研究成為一個重要課題。這種模型通過整合和分析各種數據源，從歷史數據中找出規律，能夠讓管理者更好地了解資源需求、成本結構、預算影響因素等，從而為高校管理者作出更明智的決策提供支持。

一、高校預算管理現狀

首先，高校的經費主要來源于財政撥款、學費、科研項目等方面，但某些學校或地區的經費來源相對有限，導致預算緊張。而且，政策和經費分配機制的改變，也可能引起高校預算的波動，給預算管理帶來不確定性。其次，在高校預算編制過程中，各個部門或學院對自身的需求和實際情況了解更詳細，而中央預算部門則面臨著信息不對稱的問題。這可能導致預算分配不公平或無法滿足特定部門的需要，影響預算管理的公正性與準確性。再次，高校在預算執行中，可能存在制度執行不到位的問題。預算執行需要嚴格遵循相關規章制度和流程，確保資金使用的合法性和規范性。然而，一些高校可能缺乏有效的內部控制機制或監督機構，導致預算執行不夠規范，出現經費浪費、濫用等問題。最后，預算編制與實際需求之間存在差距。高校在預算編制過程中，對實際需求的估計不準確。由于各項需求和變動較為復雜，預算編制過程中的估算可能存在偏差，導致出現一些項目的優先級錯位、資源分配不合理等問題。

二、以預算管理為主線的內部控制模型

ARMA 模型設計預算編制管理系統的引入，不僅僅是技術層面的創新，更是對高校預算管理策略的革新。傳統的預算編制往往基于經驗和主觀判斷，容易受到主觀偏見和不確定性因素的影響。而應用ARMA 模型后，能夠以客觀數據為支撐，消除主觀因素的干擾，提高預算編制的科學性和準確性。高校基于ARMA 模型設計的預算編制管理系統，能夠幫助高校對過去的財務數據進行詳細分析，識別出存在的問題和潛在的風險，從而及時采取適當的財務措施，調整預算策略，更好地應對日益復雜的財務環境和不確定的經濟形勢。這樣一來，高校能夠更加靈活地應對外部環境的變化，確保預算順利執行。

此外，基于ARMA 模型設計的預算編制管理系統，還能提高預算的透明度和可追溯性。系統可以記錄并跟蹤預算編制的過程，詳細記錄每一項預算管理措施的決策依據，使整個預算編制過程變得更加透明，降低高校財務審計難度。這不僅有助于高校內部對預算的監督與管理，而且能夠提升高校預算的公信力，加強各方對高校財務管理的信任。

為解決高校預算管理過程中出現的一系列問題，除了對財務管理制度體系進行優化，相關工作人員還積極嘗試以數據驅動為內核，構建高校預算管理模型，利用ARMA 模型捕捉時間序列中的自回歸（Autoregression,AR）和滑動平均（Moving Average,MA）數據，滿足高校預算管理復雜的數據需求。同時，為使預算管制管理系統與高校財務情況相符，相關工作人員引入以預算管理為主線的內部控制模型，通過這種方式實現數據驅動與內部控制之間的深度融合。

預算管理內部控制模型是指為有效管理和控制預算過程中的風險和不確定性，確保預算的準確性、可靠性和合規性而采取的一系列措施。

首先，控制環境是預算管理內部控制模型的基礎，既包括組織的價值觀、管理層的承諾和透明度等方面，也包括在企業內形成正確的預算管理意識，明確權責清單和職責分工，制定明確的預算政策和程序等。營造積極的控制環境，能夠促進預算管理的有效實施。其次，預算策劃是確保預算目標對齊和有效資源配置的關鍵步驟，包括確定預算目標、制定預算指標、制訂預算計劃和預算編制等過程。在預算策劃階段，需要合理分析和評估各項預算的需求與效益，確保預算的合理性和可行性[1-2]。最后，預算評估和審計作為針對預算管理內部控制模型的監督與評估過程，包括對預算執行情況的定期評估和審計，并及時發現問題和改進的機會。預算評估和審計可以通過預算績效評估、內部審計和外部審計等方式進行，其能夠提供對預算管理有效性和合規性的獨立評價，幫助改進預算管理過程。

三、基于ARMA 模型設計預算編制管理系統

經濟環境的不穩定性、市場需求和競爭態勢的變化、內外部風險等因素都會對預算編制產生影響。傳統的預算方法往往未充分考慮這些不確定因素，導致預算編制的準確性和實效性下降。為解決這一問題，研究人員嘗試引入基于ARMA 模型的預算編制管理系統。ARMA 模型結合自回歸（AR）和滑動平均（MA）模型的優點，對時間序列數據進行擬合和預測，更好地應對數據的波動和趨勢。該模型具有較好的適應性和可解釋性，能夠捕捉數據的周期性和趨勢性。將ARMA 模型應用于預算編制管理系統，可以通過對歷史財務數據進行建模和分析，提供更準確的預測和決策支持。基于ARMA 模型的預算編制系統可以考慮時間序列數據的相關性和趨勢，有效預測未來的財務狀況、收入和支出變動等。同時，ARMA 模型還能夠識別異常波動和季節性變動，進一步促使預算編制精細化。

（一）ARMA 模型原理

定義1：設平穩隨機序列為{Xt}，其滿足下列隨機差分方程：

方程（1）中的{εt}代表隨機干擾序列，φ0為均值項，θ1,θ2,…,θp代表自回歸系數，θ1,θ2,…,θq代表滑動平均系數，如果滿足E(εt)=0，Var(εt)=σε2以及E(εtεs)=0 三項條件，則表示{Xt}屬于ARMA 序列，記為ARMA(p,q)。

定義2：如果方程（1）中的θ1=θ2=θq=0，則可以得到下列方程：

方程（2）中的平穩隨機序列{Xt}為自然回歸序列，因此該模型也被稱為自然回歸模型。

（二）ARMA 建模過程

建立ARMA 模型的過程通常包括數據序列平穩化處理、分析差分后數據的相關性并進行隨機性檢驗以及相對最優階的確定，如圖1 所示。

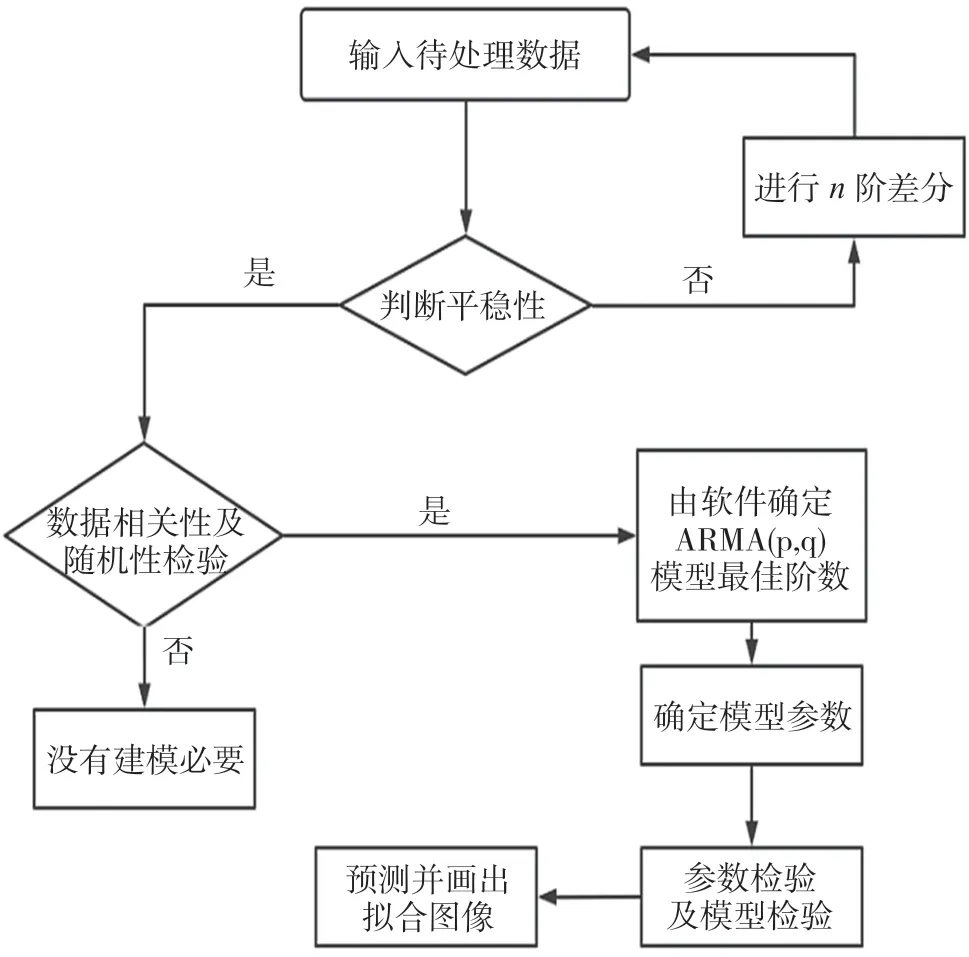
圖1 歷史數據序列建模

1.數據序列平穩化處理

首先，在建立ARMA 模型之前，需要對原始數據進行平穩化處理。平穩化處理的目的是消除數據中的趨勢性和季節性干擾，使得數據的均值和方差保持穩定。平穩化處理的方法包括差分法和對數變換等[3]。差分法可以通過計算數據的一階差分、二階差分等來消除趨勢性；對數變換可以將非線性的數據轉化為線性關系，使得數據更具平穩性。

2.分析差分后數據相關性并進行隨機性檢驗

對平穩化后的數據進行分析，包括分析差分后數據的相關性和進行隨機性檢驗。相關性分析可以通過自相關函數（ACF）和偏自相關函數（PACF）來進行。ACF表示當前觀察值與之前觀察值之間的相關程度，PACF則表示在排除了其他階的相關影響后，當前觀察值與之前觀察值之間的相關程度。相關性分析能夠幫助確定ARMA 模型的階數。

隨機性檢驗是為檢查差分后的數據是否滿足隨機性假設。常用的隨機性檢驗方法有Ljung-Box 檢驗和Q-統計量檢驗等。這些檢驗方法可以檢驗數據的殘差序列是否存在自相關性，進而判斷數據是否具有隨機性。

3.相對最優階確定

相對最優階是指在滿足模型擬合效果好的前提下，選擇較少的自回歸階數和滑動平均階數。通常采用信息準則（如赤池信息準則、貝葉斯信息準則）來進行模型選擇，選取具有較小信息準則值的ARMA 模型作為相對最優階。

四、實證分析

為驗證該模型有效性，研究人員以X 大學為例，將該大學十年的財務數據導入該模型（見表1）。

表1 X 大學十年財務數據 單位：萬元

ARMA 模型的表達式如下：

方程（3）中，u代表均值項，n=10。將表1 中的數據代入公式，則可以得到下列表達式：

基于方程（4），可以得到之后六年的預測值，將預測值與高校財務部門統計的數據進行對比，如圖3 所示。

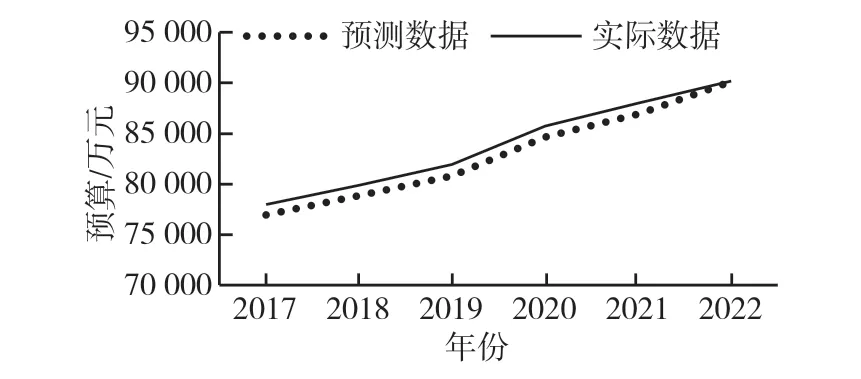
圖3 2017—2022 年預測數據與實際數據對比

分析圖3 可以發現，X 大學2016—2021 年預測財務支出與實際資金支出的誤差率小于5%，2022 年預測數據與實際數據的誤差率小于1%，且每年的預測數據走勢較為平滑，證明該模型得到的預測數據可靠性較高。學校管理者根據該模型，可以計算若干年內的財務支出情況，并根據該數據制定相應的預算管理策略。

五、基于ARMA 模型預測結果的預算管理優化措施

（一）引入績效管理

績效管理以實現目標為導向，通過設定明確的績效指標和評價體系，激勵各部門和個人在預算使用中的高效與創新表現。針對高校的教學、科研和社會服務等方面的特點，可以制定相應的績效考核標準。例如，制定教學質量評估指標，將教師的課堂教學、學生畢業率和就業情況等納入績效考核，以確保預算資金用于提高教學品質，改善教學環境。

（二）設立預算編制與審核專門機構

為確保預算編制的科學性和規范性，建立專門的預算編制與審核機構是必要的。該機構應由具備預算管理和財務分析專業知識的財務專業人員組成，他們主要負責制定預算編制準則和審核程序，并對預算進行全面的審查和評估。同時，他們還應協調各部門之間的預算編制工作，確保預算的整體合理性與協調性。此外，預算編制與審核機構還可以提供指導手冊，加深各部門與個人對預算編制和審核的理解。

（三）加強預算執行監控

建立有效的監控機制可以幫助高校及時了解預算執行情況，并進行實際支出與預算支出的比較分析。例如，可以定期進行財務報告審計和績效評價，通過這些手段，發現預算執行中的偏差，并及時采取糾正措施。此外，還可以通過預算執行監控評估預算的有效性和資源的利用效率，為未來進行預算編制提供依據。

（四）強化預算信息公開

建立高校預算信息公開平臺，定期向師生和社會公開預算編制、執行和決策過程中的關鍵信息是一項重要措施。該平臺可以公開預算編制的基礎數據、分配原則、編制依據，以及各項重要預算指標的實際執行情況和效果評估結果[4-5]。

六、結語

本研究基于數據驅動的高校預算管理模型，通過對大量歷史數據的分析和建模，揭示了預算規劃、執行與監控等環節的關鍵因素和模式。在未來的研究和實踐中，需要進一步完善和優化這一基于數據驅動的高校預算管理模型，進一步豐富數據源，包括教學、科研、學生等多個維度的信息，以提高模型的準確性和可靠性。在此基礎上，加強與實際預算管理的結合，將研究成果轉化為實際的管理實踐，不斷推動高校預算管理水平的提升。