指向深度學習的高中數學課堂學習共同體構建研究*

陸 麗

? 江蘇省太倉高級中學

《普通高中數學課程標準(2017年版2020年修訂)》指出,教學中要關注育人目的,注重培養學生核心素養,提高學生綜合運用知識解決實際問題的能力,幫助學生把握學習的深度[1].深度學習提供了開展素養導向學習的一條重要途徑.深度學習強調學生的主體立場與有意義的學習;強調對“四基”的深度加工與理解;強調問題的深度探究與思考;強調有效的學習遷移和問題解決;強調活動的深度參與與體驗;強調教學的育人功能與目標.

目前,高中課堂教學過程存在壓縮化現象,從教學目標、教學內容、教學進度、教學設計和教學過程來看,學生雖已沒有虛假學習現象,但學習動機還是外在驅動的,學習認知處于淺表層,學習中還存在“不理解”和“夾生”,課堂中批判性的反思和思考較少,思考的惰性使學生學習不能深入,真正的學習能力得不到提升.課堂上師生間的互動也存在不和諧的現象,學生自主思考與合作交流的時間較少,只能被動接受數學知識.這樣不僅制約了學生對數學知識的認知與思考,而且降低了課堂效率.其實,學生習得知識并不是課堂教學的真正目的,而是通過學習知識,了解知識背后孕育的思想方法、意義和價值.在課堂上,如何有效開展教學活動,以助推學生的思維發展?筆者結合自己的教學實踐,探索出以指向深度學習為目標、助推學生思維發展為核心、培養學生終身學習研究能力和團隊精神為抓手的教學模式——指向深度學習的高中數學課堂學習共同體模式,與同行共同探討.

1 指向深度學習的高中數學課堂學習共同體模式的主要內涵

深度學習是一種基于理解的學習,是指學習者圍繞學習主題積極主動地、批判性地學習新的知識和思想,全身心積極參與、體驗成功、獲得發展,既能將已有知識遷移到新情境中,又能將所學知識融入原有認知結構中的有意義的學習.數學深度學習強調對數學知識本質的理解以及對數學知識內在聯系的認識與把握,追求有效的學習遷移和問題的解決,屬于以深層思維為主要認知活動的學習.

共同體是具有共同愿景的個人或組織,圍繞共同的發展目標結成的具有較強互補性的團隊或聯盟.課堂學習共同體是指在課堂教學環境中,由教師和學生共同構成,以學生為本位、以“學”為中心的新型課堂教學組織形式.它以學習資源為載體,在民主和諧的學習情境中,強調師生以共同愿景為基礎,以師生間活動性、合作性、反思性的協作為學習方式,以真實任務為核心,通過對話、協作、補充、競爭,分享師生的情感、智慧、體驗與觀念,從而達到共識、共享、共進,實現知識的深度學習和個體的真正成長.

“指向深度學習的高中數學課堂學習共同體”課堂模式旨在以深度學習為目標,在以深層思維為主要認知活動的課堂氛圍中,追求問題探究的深度性、思維品質的深刻性與批判性以及情感投入的深沉性,師生以協作、共享、補充等行為獲得對數學知識本質的深度理解及運用.

2 指向深度學習的高中數學課堂學習共同體模式的教學實施方略

2.1 概念研學,助推學生思維走向融通

從概念理解的角度來看,概念的學習本身就是一個“同化”或“順應”的過程,“同化”或“順應” 是通過概念間的聯系來實現的.從教與學的角度來看,概念間的邏輯聯系應該成為最有效的聯系,這種聯系的確定不僅能促進學生思維的深度參與,亦能幫助學生建立牢固的概念知識網絡[2].因此,對于概念研學應充分利用概念間的邏輯關聯設置有價值的問題,幫助學生主動建構概念.我們可以構建課堂學習共同體實現成員間的“研學對話”,在合作學習中學生經歷概念的生成和發展全過程,在親身體驗中形成自己的見解;在同伴的分享中學生獲得概念的深度思考,在質疑批判中尋求問題的答案;在交流展示中學生獲得表達能力和反思性思維能力的鍛煉,在研究學習中構建融通的認知結構.教師作為課堂學習的主導者,也是共同體成員的助學者,在充分傾聽學生看法或問題的基礎上將學生與文本、學生與學生、教師與學生、學生與認知經驗進行串聯,引發學生深度思考,形成學習共同體的思維共振,促進師生共同成長.

案例1曲線的切線概念研學

曲線的切線對微積分的發現以及幫助學生直觀理解導數的概念都起到重要的作用.曲線的切線問題也是歷年高考考查的熱點和重點,如果學生對曲線的切線概念不理解,那么這些高考試題就難以攻破.在高三復習教學中,為了讓學生深度理解曲線的切線的概念,筆者設計了以下三個問題.

問題1曲線的切線是如何定義的?

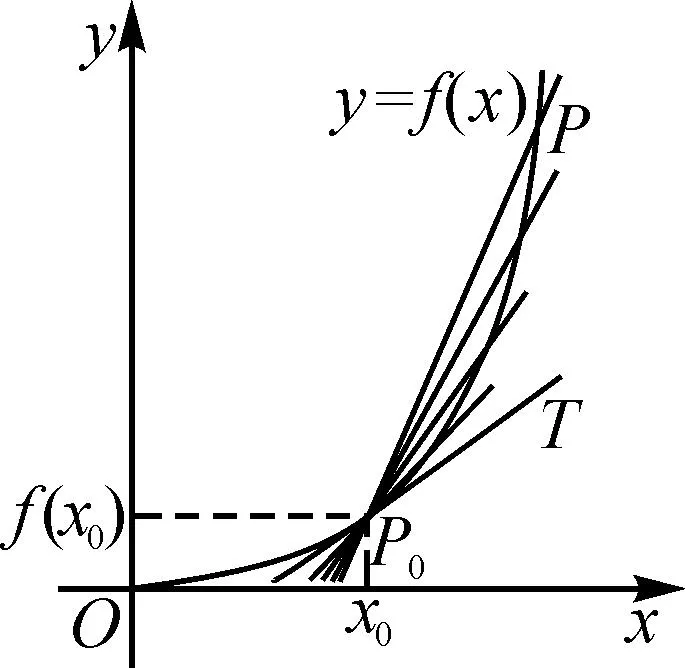
圖1

設計意圖：檢測學生對曲線y=f(x)在點P0(x0,f(x0))處的切線及切線斜率的認知程度.理解當點P(x,f(x))沿著曲線y=f(x)無限趨近于點P0(x0,f(x0))時,切線P0T是割線P0P的極限位置(圖1)、切線P0T的斜率是割線P0P斜率的極限值.讓學生體會導數中的“以直代曲”和“無限逼近”思想.

問題2能否以直線與曲線公共點的個數來判定該直線是否為曲線的切線?

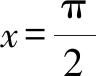
問題3曲線的切線都在曲線的一側嗎?即曲線y=f(x)在點P0(x0,f(x0))處的切線是y=g(x),則有f(x)≥g(x)或f(x)≤g(x)嗎?若正確,請證明;若錯誤,請舉出反例.

設計意圖：通過問題2的舉例以及幾何畫板的演示,容易發現曲線的切線不都在曲線的一側.筆者追問有沒有哪些曲線的切線在曲線一側,在學生認知范圍內很容易舉例說明.比如,函數f(x)=ex在各點處的切線y=g(x)都在曲線下方,滿足f(x)≥g(x).再比如,函數f(x)=lnx在各點處的切線y=g(x)都在曲線上方,滿足f(x)≤g(x).筆者再次追問一般滿足什么特征的曲線會有這樣的性質,最終得到上凸、下凸函數與切線放縮的一般性結論.上凸函數與切線放縮(圖2):若函數f(x)在定義域I上可導,且f′(x)在定義域I上可導.若f″(x)≤0恒成立,則?x0∈I,f(x)≤f′(x0)(x-x0)+f(x0)恒成立.下凸函數與切線放縮(圖3):若函數f(x)在定義域I上可導,且f′(x)在定義域I上可導.若f″(x)≥0恒成立,則?x0∈I,f(x)≥f′(x0)(x-x0)+f(x0)恒成立.師生合作共同給出了證明.

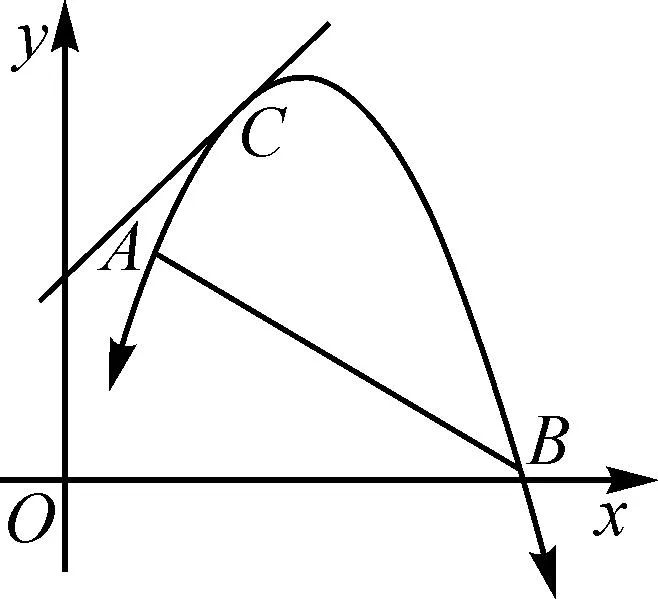
圖2

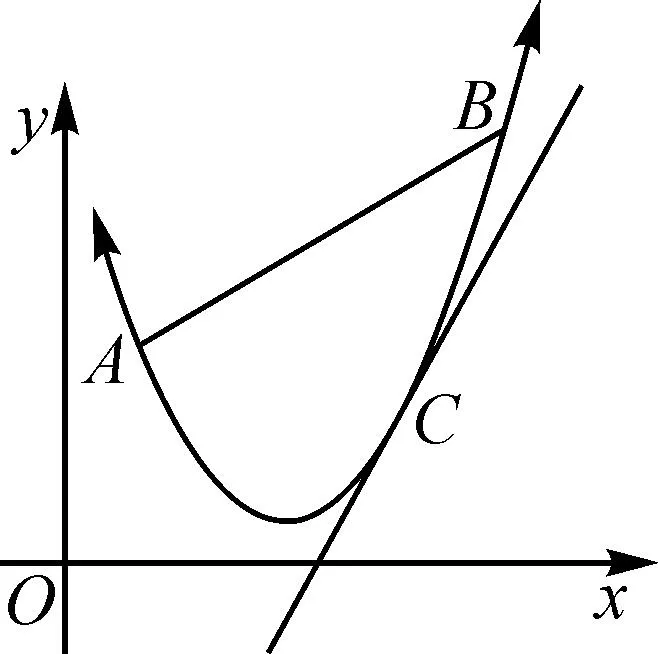
圖3

2.2 本質探源,助推學生思維走向深刻

新課程改革強調對數學本質的深刻理解.在課堂教學中,不僅要揭示數學概念、定理、法則的生成與發展過程,還要對數學問題進行深層次加工,引導學生通過深度體驗和深度思考,深刻理解數學知識的內涵與外延,深刻領悟蘊涵的數學思想與方法,使思維不斷深入,讓學習不是單純的模仿和機械的訓練,而是成為一種“再發現、再創造”的深度學習過程.

案例2求曲線的切線本質探源

求曲線的切線問題主要涉及求曲線切線的斜率與方程、切線的條數、公切線問題,以及由切線滿足的條件求參數或參數范圍.在高三復習教學中,為了讓學生深度理解曲線的切線問題的求法,筆者設計了以下問題.

問題4已知曲線f(x)=ex.則f(x)過點(-1,0)的切線方程為______.

設計意圖：讓學生體會“在”一點處的曲線切線與“過”一點的曲線切線的區別,理解曲線的切線問題關鍵是抓住切點,運用切點的三個性質(切點處的導數等于切線的斜率、切點在切線上、切點在曲線上)就可求其切線,即曲線f(x)在切點P0(x0,f(x0))處的切線方程是y-f(x0)=f′(x0)(x-x0).

2.3 問題拓展,助推學生思維走向靈活

在教學中,課堂上師生對話大多數是通過問題思考實現的,通常會經歷“提出問題—思考問題—回答問題—反饋評價”這一系列流程.問題的提出者可以是教師,也可以是學生,教師應鼓勵學生發現并提出問題.當然,在思考問題前有必要判斷一下問題是否貼合教學內容、是否能有效促進知識的生成.因此,教師應以課堂學習共同體為抓手,設置精準、開放且有效的問題,引領學生思維走向靈活.

案例3用曲線的切線問題拓展

用曲線的切線可以研究函數最值、不等式恒成立、函數零點等問題.在用切線法解題時可以全面考查學生直觀想象、邏輯推理、數學運算等素養,因此這類試題一直備受高考命題者的青睞.在高三復習教學中,為了讓學生深度理解用曲線的切線來解題,筆者設計了以下四個問題.

問題5過點(a,b)作曲線f(x)的切線有且僅有一條嗎?思考該問題,嘗試編制出與曲線f(x)=ex有關的切線問題,并給出解答.

學生編題1:過點(a,b)作曲線f(x)=ex的切線,研究切線的條數.

問題6過點(-1,0)的直線與曲線f(x)=ex交點的情況如何?思考該問題,嘗試編制出與曲線f(x)=ex有關的切線問題,并給出解答.

學生編題2:已知不等式ex≥a(x+1)對x∈R恒成立,則實數a的取值范圍為______.

學生編題3:已知方程ex=a(x+1)有兩個不等的實根,則實數a的取值范圍為______.

學生編題4:已知方程ex=ax2在(0,+∞)只有一個實根,則實數a的值為______.

問題7仿照問題5和問題6,嘗試編制出與曲線g(x)=lnx有關的切線問題,并給出解答.

學生編題5:過點(a,b)作曲線g(x)=lnx的切線,研究切線的條數.

學生編題6:已知曲線g(x)=lnx,則g(x)過點(0,-1)的切線方程為______.

學生編題7:已知不等式lnx≤ax-1對x>0恒成立,則實數a的取值范圍為______.

學生編題8:已知方程lnx=ax-1有兩個不等的實根,則實數a的取值范圍為______.

學生編題9:已知方程lnx=ax2在(1,+∞)只有一個實根,則實數a的值為______.

學生編題10:試討論曲線g(x)=lnx與y=ax2(a>0)公切線的條數.

問題8嘗試編制出與曲線f(x)=ex和g(x)=lnx有關的切線問題,并給出解答.

學生編題11:若直線l與曲線y=f(x)和y=g(x+2)都相切,則直線l的方程為______.

學生編題12:試判斷曲線y=f(x)與y=g(x)公切線的條數.

學生編題13:當a≤2時,證明f(x)>g(x+a).

學生編題14:若f(x+a)+a≥g(x)對x∈R恒成立,則實數a的取值范圍為______.

設計意圖：設置開放性問題,并嘗試讓學生編題,旨在啟發學生立足問題再拓展,于引申中品味,于編題中發現,于比較中鑒別,于反饋中深入,于拓展中激發,于聯想中感悟,于創新中陶冶,讓學生在編制試題和問題解答中經歷多次螺旋式循環探究,不斷地進行有意義的知識與方法的構建而達到舉一反三、觸類旁通之效[2].

2.4 總結延伸,助推學生思維走向廣闊

課堂以活動為抓手,讓學生在探究中理解并掌握知識,并能靈活運用到解題中去.在數學活動中要想更好地達成教學目標,就需要及時歸納、總結與反饋,不斷生成核心知識及框架體系,讓學生從“知其然”到“知其所以然”,再到“知其何由所以然”,從而助推學生的思維走向廣闊.

案例4曲線的切線總結延伸

掌握曲線的切線問題需要攻破三個難點:一是什么是曲線的切線;二是怎么求曲線的切線;三是如何用曲線的切線.筆者在問題解決中逐層顯現思維結構圖(圖4),旨在讓隱性的思維變外化顯現、抽象的思維變形象可視、零散的思維變整體有結構[3],使學生在大腦中把曲線的切線問題的知識、方法與思想逐步建立起來,真正實現“深度學習,發展素養”.

總之,數學教學不僅要讓學生掌握數學知識,更重要的是要讓學生的思維得到切實有效的提升.在“指向深度學習的高中數學課堂學習共同體”課堂上,教師精心設計教學策略,引導和激勵學習共同體自覺研究數學問題,在問題解決中學生的思維活動由表層數學知識轉向數學思想方法的形成過程,進而實現深度學習.