專題教學：讓問題在對話追問中漸次展現

楊晨

［摘? 要］ 圍繞某一道難題（比如“圓幣滾動”問題）教學，如果只是“就題講題”，那么過一段時間學生就會遺忘；如果先找出這道難題的一些同類題，并將它們改編為題組，每一個題組下的系列問題伴隨著教學進程漸次展現，那么學生在一題多變、多題歸一的專題教學中就能掌握一類問題的解答策略，悟透這類問題的深層結構.

［關鍵詞］ 專題教學；圓幣滾動；對話追問

在本校最近一次九年級期中考試的試卷中，有一道得分率很低的填空題：

將兩枚同樣大小的圓幣放在桌上，固定其中一枚，而另一枚則沿著其邊緣滾動一周，這時滾動的硬幣滾動了_____圈.

很多學生表示這道題無從入手，不會思考. 為此，筆者在中國知網中檢索相關文獻［1］，受其啟發，圍繞“圓幣滾動問題”研制了一節專題課，以期幫助學生想深、學透這類問題.

“圓幣滾動”專題課教學設計

教學環節一：初步感知

問題1? 如圖1所示，設直徑為1的圓形硬幣放在原點，將硬幣沿著數軸滾動一周，點A到達點A′的位置，則點A′表示的數是幾？

教學組織：這是不同版本教材上都出現過的一個素材，引導學生回顧點A′表示的數是無理數——圓周率π. （繼續追問與變式）

追問：畫圖分析，圓形硬幣滾動一周，其圓心所經過的路徑的長度.

預設：構造圖2可得圓形硬幣的圓心所經過的路徑的長度為線段O1O2的長度，恰為圓形硬幣的周長π.

變式：圖3、圖4、圖5中的☉O均做無滑動滾動，☉O的周長為2π.

（1）如圖3所示，∠ABC=90°，AB=BC=π，☉O從☉O1的位置出發，在∠ABC的外部沿A→B→C滾動到☉O4的位置，分析☉O自轉幾周.

（2）如圖4所示，△ABC的周長為3π，☉O從與AB相切的點D的位置出發，在△ABC的邊上沿A→B→C滾動，當☉O回到出發位置時，分析☉O自轉幾周.

教學環節二：變式探究

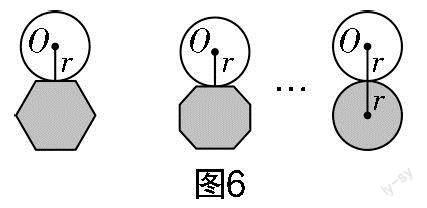
問題2? 在圖6中的系列圖形中，半徑為r的圓在周長為l的多邊形的外部順時針平滑滾動，回到出發位置時圓自轉多少周？

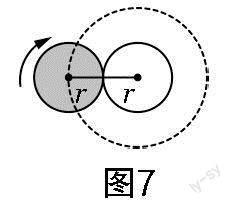
變式：（1）如圖8所示，小圓繞直徑4倍大的圓滾動一周，回到原處，小圓滾動了幾圈？

（2）如圖9所示，☉O1的半徑是☉O2的半徑的2倍，☉O1沿☉O2的周圍平滑滾動，回到原來位置時，☉O1滾動了幾圈？

教學組織：學生根據示意圖可知，只要求出☉O1的圓心所經過的路徑的長度（如圖8、圖9中的虛線圓，其周長分別為10πr和6πr），再分別除以☉O1的周長（分別為2πr和4πr），即得它們分別滾動了多少圈（分別為5圈和1.5圈）.

教學環節三：拓展提升

問題3? 如圖10所示，將4枚半徑為1的圓幣放在桌上，固定其中3枚（白色圓幣），另一枚（灰色圓幣）沿著它們的邊緣從☉O滾動到☉O′的位置，☉O滾動了幾圈？

教學環節四：課堂小結

小結問題1：本節課主要研究“圓幣滾動問題”，你對哪道習題有較深的印象，請在小組內分享各自的理解.

小結問題2：分析一些比較復雜的“圓幣滾動問題”，常常會出現一些易錯點，你在這節課中有沒有“出錯”經歷？如果有，請把你的“出錯”經歷整理出來跟大家分享；如果沒有，說說你防止“出錯”有怎樣的經驗.

教學立意的進一步闡釋

第一，聚焦主線，開展深度解題教學

專題復習課的備課選題是關鍵，所選習題一定要確保選題的“內容效度”［2］聚焦主線. 以上述課例中的問題、變式或拓展來看，筆者對“原題”進行了深度改編，比如原題中的一些問題與本節課的訓練主線不太一致，就進行了刪減，讓所有問題緊緊圍繞“圓幣滾動”而展開. 學生通過訓練后，對這類問題有了更加深刻的理解. 關于追求有深度的解題教學，主要是相對于零散出現的個別難題而言. 具體來說，如果有些難題在日常練習或講評中“就題講題”，那么過一段時間學生就會遺忘；而如果圍繞一類難題同類跟進、變式再練、舉一反三、多解歸一，那么過一段較長時間學生再遇到時，還是能識別出來并成功解決.

第二，問題驅動，漸次展開彰顯關聯

在專題教學中，當選定一些同類習題后，如果對這些同類習題進行必要的改編，使之成為驅動專題教學的“問題”，可彰顯教師的專業基本功. 一般來說，需要將入選的同類習題進行由易到難的排序，比如將較易的同類習題設置為“問題1”而出示，組織“問題1”的教學時，相機出示“變式”，但難度要控制，即學生不動筆、稍加思考就能得到思路. 在“問題1”之后拾級而上，安排“問題2”及變式，這個環節是全課的重點，要求全員思考，力爭全員學會. 在“問題3”的題組中，設置較難習題進行探究，考慮到課堂時間有限，先安排學生獨立思考，讓獲得思路的學生上臺交流，分享他們的解答過程，再請一些平時水平一般的學生復述思路、反饋學情.

第三，對話追問，切實體現“學為中心”

基于課前精心選編的“問題”驅動教學進程，要重視對話追問，在師生對話、生生對話中漸次出現系列問題，讓學生感受到問題的出現是自然而然的，體現“學為中心”的教學理念. 具體來說，當“問題”的題干出示后，有時并不急于設問，可以先問一問學生能提出怎樣的問題. 當學生提出問題后，大家再一起求解. 如果學生提出的問題不嚴謹或有錯漏，可以安排全班學生參與完善與優化. 這種開放式的教學可以有效激發學生參與課堂的興趣.

第四，解后回顧，小結問題反思提煉

專題課要重視課堂小結環節，要通過課前精心準備的“小結問題”引導學生回顧反思. 這里所指的“小結問題”一定要精準針對本課所學內容，而不是那種“空、泛”式的小結導語，如“這節課你學到了什么？”“這節課你感悟到了哪些數學思想方法？”. 以本節課中的“小結問題”為例，讓學生選出一道自己印象最深的問題，實則讓學生回顧本節課所學的全部內容. 可見，這個小結問題達到了引導學生回顧本節課所學內容的教學目的.

參考文獻：

［1］李傳富. 多角度探究一道硬幣自轉問題［J］. 中學數學，2016（02）：87-89.

［2］鄧厚波. 內容效度：章末試卷命制的關鍵指標——以人教七下“實數”章末檢測命題為例［J］. 中學數學，2019（10）：70-71.