轉(zhuǎn)化題目條件 探尋運(yùn)動路徑

蘇國東

［摘? 要］ “說題”是提升教師教學(xué)水平，促進(jìn)教師專業(yè)化發(fā)展的有效途徑. 文章從審題分析、解題過程、總結(jié)提升三部分“說”一道菱形綜合題.

［關(guān)鍵詞］ 說題；轉(zhuǎn)化條件；運(yùn)動路徑；菱形綜合題

“說題”是教師鉆研教材、探討教法、提升教學(xué)水平的有效手段，也是促進(jìn)教師專業(yè)化發(fā)展的重要途徑. 數(shù)學(xué)說題流程一般由三部分構(gòu)成，一是審題分析，包括題目涉及的知識點(diǎn)、重難點(diǎn)和關(guān)鍵點(diǎn)，分析學(xué)情，挖掘隱含條件；二是解題過程，包括解題思路和方法；三是總結(jié)提升，反思解題過程，對題目進(jìn)行必要的變式拓展.

本文從審題分析、解題過程、總結(jié)提升三部分“說”一道菱形綜合題，以期拋磚引玉.

題目? 如圖1所示，在菱形ABCD中，∠DAB=60°，AB=2，點(diǎn)E是邊AB上的一個動點(diǎn)，延長BA到點(diǎn)F，使AF=AE，且CF，DE相交于點(diǎn)G.

（1）當(dāng)點(diǎn)E運(yùn)動到AB中點(diǎn)的位置時，證明：四邊形DFEC是平行四邊形.

（2）當(dāng)CG=2時，求AE的長.

（3）當(dāng)點(diǎn)E從點(diǎn)A的位置向右運(yùn)動到點(diǎn)B的位置時，求點(diǎn)G運(yùn)動路徑的長度.

審題分析

1. 題目概述

本題是在含60°角的菱形上添加三條線段設(shè)計(jì)而成的幾何綜合題. 本題立足基礎(chǔ)知識和基本技能，發(fā)展學(xué)生的思維能力. 本題涉及的知識點(diǎn)包括平行四邊形的判定定理、菱形的性質(zhì)、相似三角形的判定定理和性質(zhì)、等腰三角形的性質(zhì)、勾股定理、銳角三角函數(shù)、點(diǎn)的運(yùn)動軌跡等，考查學(xué)生的推理能力、畫圖能力、轉(zhuǎn)化思想、方程思想等. 學(xué)生對菱形等基本圖形性質(zhì)的掌握較為扎實(shí)，具備一定的幾何推理能力，但對動點(diǎn)軌跡問題較為陌生，求解本題存在一定的困難.

2. 條件分析

本題的主干條件有：含60°角的菱形ABCD，邊長為2，AF=AE. 隱含條件是：平行相似，含60°角的特殊三角形.

第（1）問增加的條件是點(diǎn)E在AB的中點(diǎn)處，隱含條件是FE=AB=CD，對邊存在平行和相等的關(guān)系.

第（2）問增加的條件是CG=2，隱含條件是DC=CG，△CDG是等腰三角形.

第（3）問增加的條件是點(diǎn)E從點(diǎn)A的位置運(yùn)動到點(diǎn)B的位置，隱含條件是點(diǎn)E的運(yùn)動路徑、起點(diǎn)和終點(diǎn)，且點(diǎn)G隨著點(diǎn)E的運(yùn)動而運(yùn)動.

3. 重難點(diǎn)和關(guān)鍵點(diǎn)

本題的第（1）問屬于基礎(chǔ)題，解決關(guān)鍵是選擇合適的平行四邊形的判定方法. 第（2）問先要構(gòu)造相似或直角三角形，再利用方程思想、勾股定理、銳角三角函數(shù)求解. 第（3）問是動點(diǎn)軌跡問題，也是本題的難點(diǎn)，解決關(guān)鍵在于動手畫圖、合理猜想，探尋點(diǎn)G的運(yùn)動軌跡. 初中常見的運(yùn)動軌跡主要是直線形和圓弧形.

解題過程

尋找思考切入口，逐個分解、轉(zhuǎn)化題目條件，找到解題路徑和方法，完善解題過程.

1. 第（1）問的解答過程

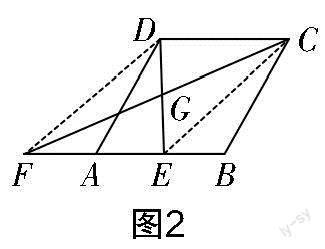
思考切入口：如圖2所示，連接DF，CE，發(fā)現(xiàn)四邊形ABCD和四邊形DFEC存在公共邊DC，利用判定方法“一組對邊平行且相等”來證明四邊形DFEC是平行四邊形.

由條件1“菱形ABCD”得知DC=AB，DC∥AB.

由條件2“AF=AE”得知FE=2AE.

由條件3“E在AB的中點(diǎn)處”得知AB=2AE，所以AB=FE.

所以DC=FE，DC∥FE，因此四邊形DFEC是平行四邊形.

2. 第（2）問的解答過程

思考切入口：由題目所給條件可知△CDG是等腰三角形，借助平行相似轉(zhuǎn)化數(shù)據(jù)，建立方程后求出線段的長.

由條件1“菱形ABCD”得知CD=CB=AB=AD=2，DC∥AB，故△DGC∽△EGF.

由條件2“CG=2，CD=2”得知△CDG是等腰三角形，根據(jù)平行相似得到△FGE也是等腰三角形.

設(shè)AE=n，由條件3“AF=AE”可得FG=FE=2n.

由條件4“∠DAB=60°”得知∠FBC=120°，于是從圖中提取一個含120°的特殊三角形FBC（如圖3所示），其中FC=2n+2，F(xiàn)B=n+2，BC=2.

3. 第（3）問的解答過程

思考1：點(diǎn)G的運(yùn)動路徑是什么？

（1）畫圖.

畫出兩動點(diǎn)的不同位置. 當(dāng)點(diǎn)E分別在點(diǎn)A，E1，E2，B處時，連接DE和CF，得到點(diǎn)G依次位于點(diǎn)A，G1，G2，G3處，如圖4所示，觀察到點(diǎn)G的運(yùn)動軌跡是從點(diǎn)A到G3的一條線段.

（2）猜想.

點(diǎn)G隨著點(diǎn)E的運(yùn)動而運(yùn)動，可看作伴隨軌跡問題，其中點(diǎn)E是主動點(diǎn)，點(diǎn)G是從動點(diǎn)，點(diǎn)E的運(yùn)動路徑是一條線段，則點(diǎn)G的運(yùn)動路徑也是一條線段. 通過幾何畫板動態(tài)演示也可以得到同樣的結(jié)果.

（3）類比.

第（1）問與第（3）問的圖形之間存在一定的關(guān)系. 第（1）問中的四邊形DFEC是平行四邊形，如圖5所示，延長AG交DC于點(diǎn)H，點(diǎn)A，G分別是FE，DE的中點(diǎn)，所以AG∥FD，點(diǎn)H是DC的中點(diǎn). 隨著點(diǎn)E的運(yùn)動，平行四邊形DFEC變成了梯形，但不難推斷點(diǎn)H仍是DC的中點(diǎn). 說明AH與定線段DC交于定點(diǎn)H，所以點(diǎn)G的運(yùn)動路徑在直線AH上.

思考2：如何用初中知識來證明點(diǎn)G的運(yùn)動路徑是一條線段？

思考切入口：根據(jù)上述思路，如圖6所示，延長AG交DC于點(diǎn)H，利用菱形中與AH有關(guān)的“8字形相似”模型，轉(zhuǎn)化線段比例關(guān)系.

結(jié)合條件2“AF=AE”得知DH=HC，所以點(diǎn)H是DC的中點(diǎn)，為定點(diǎn)，所以點(diǎn)G在直線AH上運(yùn)動.

由條件3“點(diǎn)E從點(diǎn)A的位置向右運(yùn)動到點(diǎn)B的位置”得知點(diǎn)E的起點(diǎn)為A，終點(diǎn)為B，所以點(diǎn)G的起點(diǎn)為A，終點(diǎn)為K，如圖7所示，即點(diǎn)G的運(yùn)動路徑為線段AK.

思考3：如何求線段AK的長？

思考切入口：利用三角形相似的性質(zhì)、勾股定理、銳角三角函數(shù)等求線段AK的長.

在菱形ABCD中，∠DAB=60°，點(diǎn)H為DC的中點(diǎn)，連接BH構(gòu)造直角三角形HBC.

此外，通過構(gòu)造其他輔助線也可求得AK的長（如圖9、圖10所示）.

思考4：能否建立平面直角坐標(biāo)系，用代數(shù)法解決幾何問題？

思考切入口：求兩直線的交點(diǎn)，即聯(lián)立直線方程求公共解；求線段的長，可使用兩點(diǎn)間的距離公式.

總結(jié)提升

1. 反思解題過程

本題三個小問的難度呈梯度變化，體現(xiàn)“使不同層次的學(xué)生得到不同發(fā)展”的理念. 第（1）問從已知四邊形和待證四邊形存在公共邊的角度入手，通過“一組對邊平行且相等”判定平行四邊形. 第（2）問挖出隱含條件，借助平行相似、等腰三角形等知識，提取基本圖形，構(gòu)造含120°角的特殊三角形，運(yùn)用勾股定理、銳角三角函數(shù)求解. 第（3）問通過動手畫圖、猜想驗(yàn)證和嚴(yán)謹(jǐn)推理，明晰動點(diǎn)的運(yùn)動軌跡，逐步分解轉(zhuǎn)化難點(diǎn)，利用幾何和建系的方法求解，滲透著數(shù)形結(jié)合思想方法，是初高中知識銜接的良好體現(xiàn).

2. 變式

第（3）問可變式如下.

（1）改變問題（條件相同）.

變式1：求點(diǎn)G的運(yùn)動路徑長度的取值范圍.

變式2：求點(diǎn)G到AB的最大距離.

變式3：求△ABG面積的最大值.

（2）改變背景.

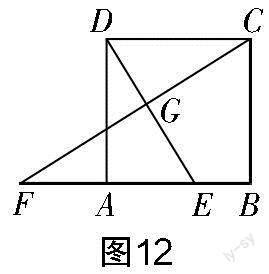
變式4：如圖12所示，在正方形ABCD中，AB=2，點(diǎn)E是邊AB上的一個動點(diǎn)，延長BA到點(diǎn)F，使AF=AE，且CF，DE相交于點(diǎn)G. 當(dāng)點(diǎn)E從點(diǎn)A向右運(yùn)動到點(diǎn)B的位置時，求點(diǎn)G運(yùn)動路徑的長度.

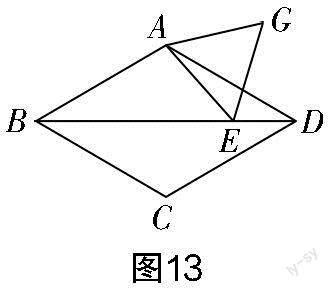
變式5：如圖13所示，在菱形ABCD中，∠ABC=60°，點(diǎn)E是對角線BD上的一個動點(diǎn)，以AE為邊作等邊三角形AEG. 當(dāng)點(diǎn)E從點(diǎn)B的位置向右運(yùn)動到點(diǎn)D的位置時，求點(diǎn)G運(yùn)動路徑的長度.

變式6：如圖14所示，在正方形ABCD中，AB=2，點(diǎn)E是邊AB上的一個動點(diǎn)，△DEF為等腰直角三角形，點(diǎn)G是斜邊DF的中點(diǎn). 當(dāng)點(diǎn)E從點(diǎn)A的位置向右運(yùn)動到點(diǎn)B的位置時，求點(diǎn)G運(yùn)動路徑的長度.