同心圓錐曲線的性質(zhì)再探
官一宏


摘要:文[1]通過類比同心圓的定義,得到同心圓錐曲線的定義.受此啟發(fā),本文先從同心圓的結(jié)論出發(fā),類比到同心圓錐曲線,然后利用超級畫板進(jìn)行驗(yàn)證所得結(jié)論,最后給出結(jié)論的解析證明與幾何證明.
關(guān)鍵詞:同心圓;同心圓錐曲線;性質(zhì);探究
中圖分類號:G632文獻(xiàn)標(biāo)識碼:A文章編號:1008-0333(2023)33-0008-03
類比思想在高中數(shù)學(xué)教學(xué)中扮演著重要的角色,數(shù)學(xué)中的很多發(fā)現(xiàn)都是通過類比得到的.類比可以得到新的結(jié)論,但未必正確,需要給出嚴(yán)格的證明.同心圓,由于其對稱性而具有很多經(jīng)典的性質(zhì).根據(jù)類比思想,同心圓錐曲線應(yīng)該也有很多經(jīng)典的結(jié)論.我們可以通過類比得到結(jié)論,然后用超級畫板驗(yàn)證,最后給出嚴(yán)格的證明.
1 同心圓錐曲線的定義
定義設(shè)兩圓錐曲線有著公共的焦點(diǎn)F,且與F相應(yīng)的準(zhǔn)線f也是公共的,則稱這兩個(gè)圓錐曲線為同心圓錐曲線[1].
2 同心圓的性質(zhì)
性質(zhì)1如圖1,設(shè)圓Γ1和圓Γ2為同心圓,公共圓心為O,作一直線交圓Γ1于A、B兩點(diǎn),交圓Γ2于C、D兩點(diǎn),那么∠AOC=∠BOD.
3 同心圓錐曲線的性質(zhì)
將該性質(zhì)類比到同心圓錐曲線,則得到:
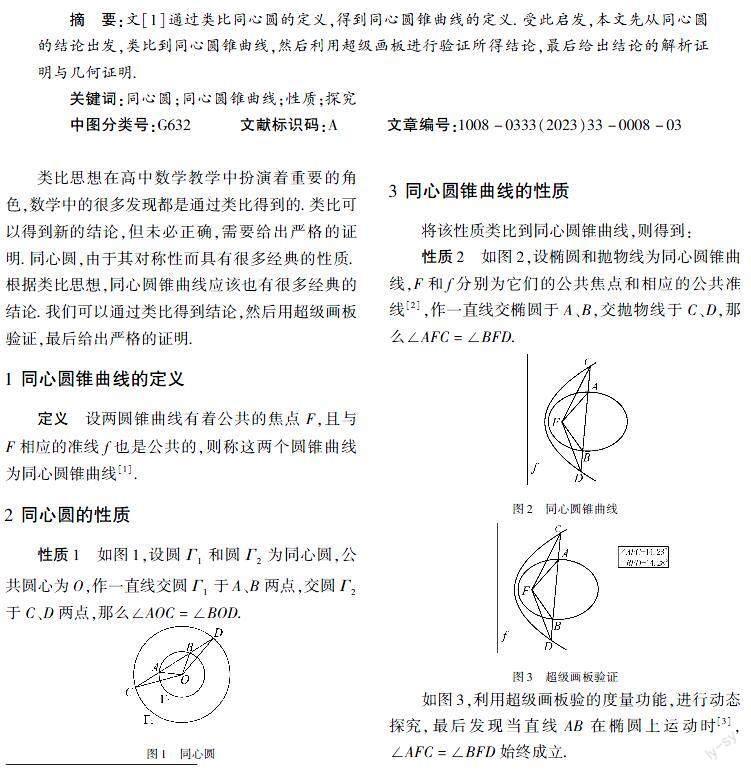
性質(zhì)2如圖2,設(shè)橢圓和拋物線為同心圓錐曲線,F(xiàn)和f分別為它們的公共焦點(diǎn)和相應(yīng)的公共準(zhǔn)線[2],作一直線交橢圓于A、B,交拋物線于C、D,那么∠AFC=∠BFD.
如圖3,利用超級畫板驗(yàn)的度量功能,進(jìn)行動(dòng)態(tài)探究,最后發(fā)現(xiàn)當(dāng)直線AB在橢圓上運(yùn)動(dòng)時(shí)[3],∠AFC=∠BFD始終成立.
4 性質(zhì)的證明
證法1如圖4,以F為坐標(biāo)原點(diǎn)建立直角坐標(biāo)系,由同心圓錐曲線的定義知p=b2c,拋物線的頂點(diǎn)坐標(biāo)為-p2,0.橢圓的對稱中心坐標(biāo)為c,0,故易得拋物線的方程為y2=2b2cx+b22c,橢圓的方程為x-c2a2+y2b2=1[3] .
因?yàn)橹本€l分別交橢圓、拋物線于A、B、C、D,故直線l不可能平行于x軸,則設(shè)l:x=my+t,Ax1,y1,Bx2,y2,Cx3,y3,Dx4,y4,直線FA、FB、FC、FD斜率分別為k1、k2、k3、k4.
由到角公式tan∠AFC=k3-k11+k1·k3,tan∠BFD=k2-k41+k2·k4.
欲證∠AFC=∠BFD,只需證tan∠AFC=tan∠BFD,即證k3-k11+k1·k3=k2-k41+k2·k4,k3-k1·1+k2·k4=k2-k4·1+k1·k3 ,
整理得k1+k2k1·k2-1=k3+k4k3·k4-1.
直線與橢圓聯(lián)立整理得:
整理得a2t2-b4m2y2+2mb4+2b2cmtxy+b2t2-2b2ct-b4x2=0.
對上式同除以x2得
(a2t2-b4m2)·(yx)2-(2mb4+2b2cmt)·(yx)+(b2t2-2b2ct-b4)=0
易知上述方程的兩個(gè)根分別為y1x1、y2x2,即為k1、k2.
則由韋達(dá)定理可得:k1+k2=-2mb4+2b2cmta2t2-b4m2,
k1·k2=b2t2-2b2ct-b4a2t2-b4m2.
同理,齊次聯(lián)立拋物線與直線l可得
b4m2-c2t2·yx2-2b2cmt+2mb4·yx+2b2ct+b4=0
由韋達(dá)定理可得:k3+k4=2b2cmt+2mb4b4m2-c2t2,
k3·k4=2b2ct+b4b4m2-c2t2.
∴k3+k4k3·k4-1=2b2cmt+2mb42b2ct+b4-b4m2-c2t2=2b2cmt+2mb4b4+2b2ct-m2b4+c2t2.
∴k1+k2k1·k2-1=k3+k4k3·k4-1,即tan∠AFC=
tan∠BFD,亦即∠AFC=∠BFD,證畢.
證法2設(shè)橢圓的方程為x2a2+y2b2=1(a>b>0),則公共焦點(diǎn)F(-c,0),公共準(zhǔn)線f:x=-a2c,由
拋物線的方程為y2=2b2c(x+a2+c22c).[3]
∠AFC=∠BFD等價(jià)于∠AFB與∠CFD的角平分線重合.
記∠AFB與∠CFD的角平分線的斜率分別為k1,k2,直線lAB:x=my+n.
設(shè)A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD).
則由到角公式,有
yBxB+c-k1+k·yBxB+c=k-yAxA+c1+k·yAxA+c,
又xA=myA+n,xB=myB+n,得
[2myAyB+(n+c)(yA+yB)](k2-1)+2[(m2-1)yAyB+m(n+c)(yA+yB)+(n+c)2]k=0將lAB:x=my+n代入x2a2+y2b2=1(a>b>0)消去x得
(a2+b2m2)y2+2b2mny+b2(n2-a2)=0.
從而有yA+yB=-2b2mna2+b2m2,
yAyB=b2(n2-a2)a2+b2m2.
所以2myAyB+(n+c)(yA+yB)
=2b2m(n2-a2)a2+b2m2-(n+c)·2b2mna2+b2m2
=-2b2m(a2+cn)a2+b2m2,
從而有 -2b2m(a2+cn)a2+b2m2(k2-1)+2k·b4m2-(a2+cn)2a2+b2m2=0,
即b2m(a2+cn)k2+[b4m2-(a2+cn)2]k-b2m(a2+cn)=0.(1)
將lAB:x=my+n代入y2=2b2c(x+a2+c22c)消去x得
c2y2-2b2mcy-b2(a2+c2+2nc)=0.
從而有yC+yD=-2b2mc,
yCyD=-b2(a2+c2+2nc)c2.
所以2myAyB+(n+c)(yA+yB)
=-2b2m(a2+c2+2nc)c2+(n+c)·2b2mc
=-2b2m(a2+cn)c2,
從而有-2b2m(a2+cn)c2(k2-1)+2k·b4m2-(a2+cn)2c2=0,
即b2m(a2+cn)k2+[b4m2-(a2+cn)2]k-b2m(a2+cn)=0.(2)
而k1是方程(1)的根,k2是方程(2)的根,但是方程(1)與(2)其實(shí)是同一方程,
所以k1=k2. 所以∠AFC=∠BFD.
證法3先證明一個(gè)引理:
如圖5,設(shè)同心圓錐曲線的焦點(diǎn)為F,相應(yīng)的準(zhǔn)線為l,任作直線交橢圓于B,C,交l于E,則EF為∠BFC的角平分線.
證明:設(shè)圓錐曲線的離心率為e,過B,C分別作BI,CJ垂直l于I,J,由圓錐曲線的第二定義知,e=CFCJ=BFBI,即CFBF=CJBI=CEBE,由外角平分線的逆定理知,EF為∠BFC的角平分線.
下面證明本題的結(jié)論,如圖6,延長諸線與l相交,對拋物線由引理有EF平分∠DFH,對橢圓由引理有EF平分∠CFG.
從而∠DFC=∠GFH=∠AFB.證畢.
通過類比同心圓的性質(zhì),可以得到同心圓錐曲線的性質(zhì)[4],然后利用超級畫板進(jìn)行驗(yàn)證,再用解析法或者幾何法給出嚴(yán)格證明,這就是本文的研究思路.我們知道,同心圓有很多漂亮的性質(zhì),那么,這些性質(zhì)類比到同心圓錐曲線是否成立呢?這有待于讀者的進(jìn)一步探索.
參考文獻(xiàn):
[1]?李鴻昌,凌禹,胡典順.高中數(shù)學(xué)核心素養(yǎng)的培養(yǎng):以“從同心圓到同心圓錐曲線”為例[J].中學(xué)教研(數(shù)學(xué)),2018(02):24-26.
[2] 李鴻昌,徐章韜.核心素養(yǎng)視角下的圓錐曲線探究:以“從同心圓到同心圓錐曲線”為例[J].中小學(xué)數(shù)學(xué)(高中版),2017(11):7-9.
[3] 李鴻昌,徐章韜.從同心圓到同心圓錐曲線:基于超級畫板的探究[J].數(shù)學(xué)通訊(下半月),2018(10):38-41.
[4] 林國紅.同心圓錐曲線中兩個(gè)命題的證明[J].中學(xué)數(shù)學(xué)研究(華南師范大學(xué)版),2019(11):33-35.
[責(zé)任編輯:李璟]

