開展變式教學，促進深度學習

陳艷陽

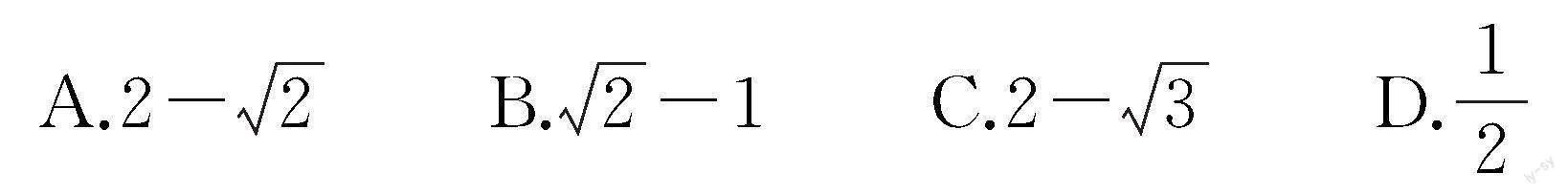
變式教學以試題改編、一題多解、知識遷移等為手段，從不同的角度引發學生對試題產生新的思考，有效鍛煉學生的思維能力，是數學教學中一種常用的訓練手段.變式教學使學生對原有的試題產生新的認識，為知識建構、實現舉一反三創造了條件，調動學生的高階思維參與學習活動，有效促進深度學習的開展，提升學習效果.

1 何謂深度學習

深度學習是指學習者圍繞學習目標積極主動地運用所學知識進行觀察、分析和探究，并主動接受新的知識，領悟其中思想，從而將新知與舊知進行整合，進一步完善知識結構，有效實現知識遷移，尋求解決問題路徑的一種學習方式.深度學習要求學習者能夠有效整合知識，注重對學習過程的反思與建構，從而培養批判性思維，發展思維的靈活性，提升解決問題的能力.

本文從八年級“直角三角形”中的一道習題出發，通過習題變式展開教學，引導學生進行知識和方法的建構與反思，從而實現深度學習.

2 指向深度學習的變式教學

2.1 例題展示與分析

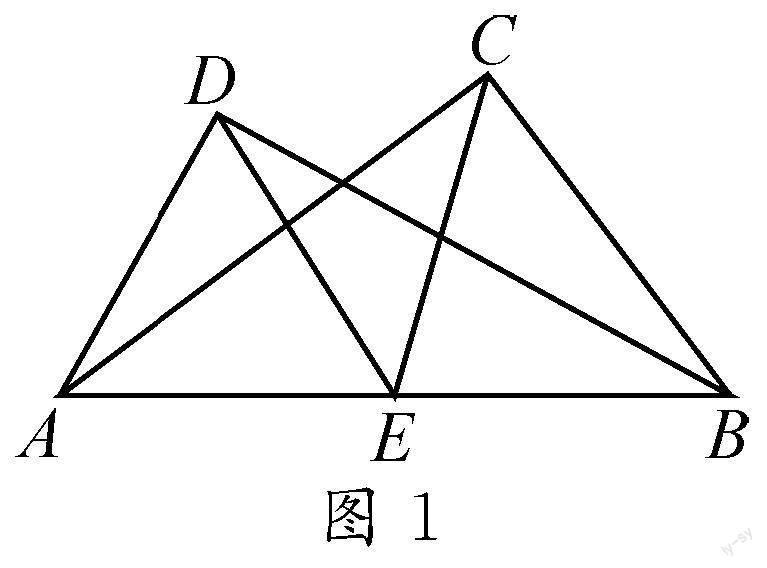
例題 如圖1，已知AD與BD垂直，AC與BC垂直，AB的中點為E，請問DE與CE是否相等，并說明理由.

解析：因為AB的中點為E，AD與BD垂直，AC與BC垂直，所以根據直角三角形斜邊與斜邊上中線的關系，可以得到DE，CE都等于AB的一半.因此，DE與CE相等.

本題考查學生對直角三角形斜邊與斜邊上中線的關系這一知識點的掌握情況，通過將兩個直角三角形疊加，找到它們共用的斜邊，構建出多種等量關系，實現相互轉化，從而找到答案.本題在結構上看似簡單，巧妙地構造出共用斜邊的直角三角形，實則結構精巧，內涵豐富.通過這道例題，學生更加深刻地掌握了直角三角形的性質定理，提升了知識運用能力.

2.2 變式教學的實踐

（1）線段關系

變式1 如圖2，已知AD與BD垂直，AC與BC垂直，AB的中點為E，CD的中點為F，證明EF與CD垂直.

分析：本題從等腰三角形的性質出發，將原題中求解線段的數量關系轉化為證明線段的位置關系，從而引導學生能夠透過現象抓住本質，運用已學知識構建數學模型，進一步理解三角形的性質定理，靈活運用知識解決問題，發展數學思維能力.

（2）角度關系

變式2 如圖3，在三角形ABC中，BD與AC垂直，垂足為D，AB與CE垂直，垂足為E，BC的中點為F，∠EFD等于50°，求∠DEF的度數.

變式3 如圖4，在四邊形ABCD中，∠ABC和∠ADC為直角，對角線AC的中點為E，連接BE，ED，BD，若∠BAD等于58°，求∠EBD的度數.

分析：變式2和變式3依托放置在不同位置的直角三角形進行設問，引導學生從不同的角度進行思考，使學生學會知識遷移，從思考線段間的關系轉變為思考角間的關系，實現思維的進階，提升學生綜合運用基礎知識的能力，進一步理解三角形的性質定理.

變式4 如圖5，在銳角三角形ABC中，AB與AC上的高分別是CD和BE，M和N分別是線段BC和DE的中點.

（1）連接DM與ME，請問∠A與∠DME之間是什么關系，并證明.

（2）如圖6，若將銳角三角形ABC變為鈍角三角形ABC，你的結論還成立嗎？請說明理由.

解析：（1）∠DME=180°－2∠A.

下面證明.由已知條件，可知BM=DM=EM=CM，因此∠ABC=∠MDB，∠ACB=∠MEC.所以∠BMD+∠CME=180°－2∠ABC+180°－2∠ACB=2∠A，故∠EMD=180°－（∠BMD+∠CME）=180°－2∠A.

（2）連接DM與ME，可以得到∠BME+∠CMD=2（∠ABC+∠ACB），經過轉化可以得到∠DME=2∠BAC－180°.

變式4通過條件的拓展，進一步探究三角形中的角度關系，考查學生從復雜問題中抽象數學模型的能力，提升分析和推理能力，進一步促進深度學習.

3 多角度設計指向知識遷移

3.1 基本圖形中的線段長度關系

變式5 如圖7，已知AC與BC垂直，BD與AD垂直，AB的中點為E，AB與CD相交于點F，假設AD與BD相等，EF，DE的長度分別為3和4，求CD的長度.

本題利用基本圖形中直角三角形共用斜邊，運用勾股定理、等面積法、等腰三角形三線合一等知識求解線段的長度，

滲透了知識遷移的思想，

使學生能夠綜合運用知識求解問題，培養思維的靈活性.

3.2 基本圖形中的坐標問題

變式6 如圖8，在三角形ABC中，∠A等于67.5°，BC的長度等于4，BE與CA垂直，垂足為E，CF與AB垂直，垂足為F，BC的中點為D.假設以F為原點，以FD所在的直線為x軸構建平面直角坐標系，則點E的橫坐標是（）.

本題在基本圖形中加入了坐標軸的知識，使學生學會將三角形的性質、勾股定理、等腰三角形與坐標軸的知識相結合，利用直角三角形共用斜邊的知識，結合線段的長度求解點的坐標，進一步發散思維，學會透過現象抓住本質，拓寬了視野，培養舉一反三和知識遷移的能力.

3.3 基本圖形中的面積關系

變式7 如圖9，已知三角形ABC中，BD和CE是高，BC邊的中點為F，連結DE，EF和DF.

（1）如果∠A等于45°，請判斷三角形DEF的形狀，并說明理由;

（2）如果∠A與∠DFE的度數比為5∶2，BC的長度為4，求三角形DEF的面積.

解析：（1）三角形DEF是等腰直角三角形.下面證明.因為BD和CE是高，BC邊上的中點為F，所以EF等于BC的一半，且與DF相等.因為∠A等于45°，所以∠EBF+∠DCF=180°－45°=135°.因為EF與BF相等，所以∠EBF與∠FEB相等，同理∠DCF與∠FDC相等.于是∠FEB與∠FDC的和為135°，所以∠BFE與∠CFD的和為90°.由此可知，三角形DEF為等腰直角三角形.

（2）作EG垂直于DF，垂足為G.設∠A為5x，則∠DFE為2x，所以∠FEB+∠FDC=∠EBF+∠DCF=180°－5x.因此可得∠BFE+∠CFD=10x，所以10x+2x=180°，解得x=15°.結合BC的長度為4，可以求得三角形DEF的面積為1.

本題涉及等腰三角形的性質和判定、三角形的內角和定理及面積公式，考查學生綜合運用知識的能力.通過變式7，進一步考查學生從綜合性問題中抽象出基本圖形的能力，有效訓練學生靈活運用知識和遷移知識的能力.根據這一變式練習，鞏固了學生對基礎圖形性質定理的掌握，同時又開闊了視野，在不同角度的知識應用中實現能力的提升和思維的跨躍.

從基本的習題出發，通過題干條件和設問內容的變化，實現變式練習，使學生能夠通過基本的活動經驗和數學思想，形成關于基本圖形的結論、解題思路和解題方法，并能夠將解題方法靈活運用到變式習題中，有效鍛煉了抽象思維能力.這樣的教學過程能幫助學生建立起一種解決問題的模型，并應用這一模型解決問題，既落實了基本的數學知識和技能，同時又發展了抽象思維能力，在積累活動經驗的同時又體驗了數學的思想和方法，在變式練習中落實了核心素養.