數形結合思想在初中函數解題中的應用

姜靜怡

摘要：函數部分是中考考查的熱點，也是初中數學教學的重難點.根據《義務教育數學課程標準（2022年版）》，中考關于函數考查的題目比例有所增加，其中應用數形結合思想解決的問題較多，給學生帶來了一定的難度.本文中以此作為研究視角，立足初中函數解題教學，科學融入數形結合思想，借助圖形的輔助，將抽象思維和形象思維結合起來，最終將復雜的函數問題簡單化，幫助學生順利解決相關函數問題.

關鍵詞：初中數學;函數;數形結合思想

1 利用數形結合思想解決函數概念問題

學習函數，首先要明確函數的概念.這就要求學生能識別簡單實際問題中的常量、變量及其意義；能根據函數圖象分析出實際問題中變量的信息，發現變量間的變化規律；能結合函數圖象分析簡單實際問題中的函數關系，進而能初步推測變量的變化趨勢.

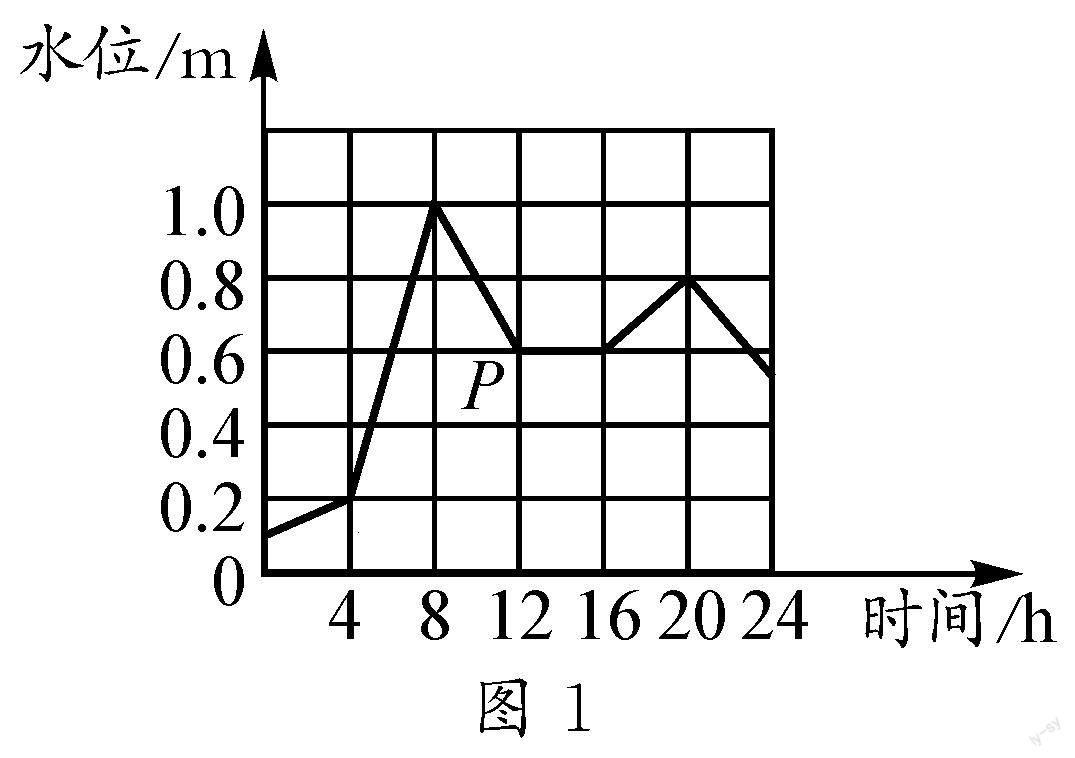
例1?最近長春市連降雨雪，某水庫水位上漲.圖1表示某一天的水位變化情況，0時的水位為警戒水位.結合圖象判斷下列敘[JP]述不正確的是（）.

A.8時水位最高

B.P點表示12時水位為0.6 m

C.8時到16時水位都在下降

D.這一天水位均高于警戒水位

解析：本題是一道典型的運用數形結合思想解決函數概念的問題.解題時要在具體情景的基礎上認真審題，結合題目給出的圖象分析得出答案.

對于A選項，通過觀察圖象可知，在8時圖象縱坐標最大為1.0.所以A選項正確.

對于B選項，在圖象中可以觀察到，P點對應的橫坐標為12，縱坐標為0.6.所以B選項正確.

在C選項中，提到了從8時到16時的水位問題.通過觀察圖象可以發現，從8時到12時水位確實在不斷下降，但從12時到16時水位沒有發生變化.所以C選項錯誤.

D選項中提到這一天水位均高于警戒水位，即高于0時水位，觀察圖象可知D選項正確.

在解決本題時，教師要提醒學生運用數形結合的思想將圖象與題干對應的信息聯系起來，進而輕松解決問題.

2 利用數形結合思想解決一次函數問題

在學習一次函數的過程中，要十分注意數形結合思想的運用.要會畫一次函數的圖象，能根據圖象和表達式y=kx+b（k≠0）探索并理解k>0和k<0時圖象的變化情況，并且能夠根據已知條件結合以往學過的知識解決實際問題.

例2 已知正比例函數y=2x的圖象上有一點B（m+2，m2－4），且點B在第一象限.

（1）求點B的坐標；

解析：（1）通過數形結合思想，利用待定系數法將點B的坐標代入正比例函數解析式，解方程即可求得m的值.將點B（m+2，m2－4）代入正比例函數解析式y=2x，得到2（m+2）=m2－4，解得m=4或-2.又因為點B在第一象限，所以m=4.故點B的坐標為B（6，12）.

（2）算出△OBC的面積為36，結合正比例函數解析式設點P（a，2a），分兩種情況討論.

當點P在線段OB上時，過點P作PD⊥BC于點D，如圖2，

則PD=6－a.

當點P在射線BA上時，過點P作PD⊥BC交BC的延長線于點D，如圖3，則PD=a－6.

綜上，點P的坐標為（3，6）或（9，18）.

3 利用數形結合思想解決二次函數問題

在初中函數的學習中，二次函數既是重點也是難點，更是中考的熱點.中考對于二次函數考查的難度也在不斷增加，在解題中，要不斷融入數形結合思想才可以更加順利地解決相關問題［1］.關于二次函數，主要考查其圖象問題，包括圖象的開口方向、對稱軸以及二次函數的最大值和最小值并確定相應的自變量的值，在此基礎上還要能夠解決簡單的實際問題.學生在學習時要更加關注二次函數解析式中各個字母代表的含義.

A.①②

B.②③

C.②④

D.③④

當x=1時，由圖象知y=2，代入解析式得a+b+c=2，所以②正確.

當x=-1時，y=a-b+c<0;由（a+b+c）-（a-b+c）>2，得b>1，所以④錯誤.

綜上所述，B選項正確.

4 利用數形結合思想解決反比例函數問題

反比例函數作為初中函數的重要組成部分，主要考查其函數解析式及函數圖象的應用，明確當k<0和k>0時反比例函數圖象的整體特征，并能基于此解決實際問題.反比例函數知識點經常與一次函數和二次函數相結合，并且解題方法也相對比較特殊.經常借助交點求解三角形的面積.

（1）求k的值及點C的坐標；

（2）在y軸上有一點D（0，5），連接AD，BD，求△ABD的面積.

總而言之，函數是初中數學學習的一個難點，它也是考試的重點.對于學生在解決函數問題的過程中經常出現的一些錯誤，要給予他們足夠的引導和啟發，在解答問題的時候，將數形結合思想與問題直觀融合起來，利用圖形的幫助，將抽象、復雜的函數問題形象地展示出來，以便讓學生能夠更好地理清解題思路，從而更好地完成問題的解答.與此同時，在數形結合思想的幫助下，學生也實現了對數學知識的內化，推動了數學思維的發展，從而數學綜合素質也得到了提高.總之，數形結合思想的合理應用，對于初中數學函數解題具有很大幫助.因此，具體教學中，教師應根據實際情況，引導學生通過合理的數學思維進行解題.這樣才可以獲得更好的教學效果，促進初中生數學學科的良好學習與發展[2].

參考文獻：

［1］楊遠鴻.數形結合思想在初中數學解題中的應用——以初中函數問題為例[J].數理天地（初中版），2023（1）：52-53.

［2］曹峰.初中數學解題中的函數思想應用策略[J].數理天地（初中版），2023（9）：26-27.