規不正，不可為圓

郝占峰

“規不正，不可為圓”闡明了遵守規則的重要性，也從側面反映了規范化解題的積極意義.規范化解題不僅能提升初中生數學解題效率，還能通過規范化審題、解題步驟書寫以及解題答案求算等，發展學生的邏輯思維能力，輔助學生建構科學完整的數學解題模型，進一步強化學生知識綜合運用能力，以滿足素質教育對學生邏輯思維、推理分析等學科思維能力的發展要求.

1 初中數學解題規范化教學的積極意義

1.1 有助于提升學生解題效率

解題規范化教學活動的開展，有助于提升初中生數學解題效率.這主要是因為解題規范化教學活動的開展，使得學生審題、解題更為規范細致，精準掌握數學問題題干所給予的條件以及解題目的，進而掌握解決問題的思路方法，并做到科學嚴謹地處理數學問題，規范化書寫解題步驟，精準求出最終答案.這樣學生就能有效避免由于解題不規范而造成的解題錯誤、失分現象，實現數學解題效率的顯著提升.

1.2 有助于翻轉師生課堂角色

解題規范化教學活動的開展，有助于鞏固強化學生課堂學習的主體地位.相較于傳統的應試式解題教學活動，解題規范化教學活動與學生個體聯系更為緊密，大多數情況下都是基于不同學生個體的實際情況，針對性開展解題規范化教學活動，旨在個性化提升學生的規范化解題能力，確保所有層次學生都能按照自身的解題習慣，科學提升個人數學解題的規范性，而不是一刀切地完成所布置的解題規范化學習任務.這樣無形中便提升了學生在解題規范化教學活動中的主體地位.由此可見，數學解題規范化教學活動的開展，有利于推進數學課堂師生角色地位的翻轉.

1.3 有助于轉變教師教學思想

解題規范化教學活動的全面落實，能逐步轉變教師的解題教學思想.教師作為解題規范化教學活動的引導者，要想更好地推進規范化解題活動，應降低應試教育等傳統教育思想觀念對個人解題規范化教學指導工作產生的消極影響.教師往往會積極學習素質教育、解題教學規范化等育人理念，掌握規范化解題教學的核心，逐步轉變個人的解題教學思想，以實現教育思想轉變導向數學解題規范化教育手段改革，最終達到充分發揮教師規范化解題教學指導效能目的.因此，規范化解題活動的開展，有利于逐步轉變教師的解題教學思想.

2 初中數學解題規范化教學的具體策略

2.1 傳授規范審題方法，輔助學生正確理解題干

審題作為解題的第一個環節，其規范與否直接影響著學生對題目題干條件的理解程度，決定著后面每一個環節解題活動能否順利開展，故此環節的解題教學規范化影響極為深遠.同時，審題規范化技巧的傳授，能幫助學生精準高效掌握數學問題的題干核心，弄清數學問題各個條件之間的邏輯關系，為后續問題的深度思考分析提供方向，是學生解題規范化學習參與不可或缺的一環.為此，教師可先在解題規范化教學活動中，傳授給學生一些審題的方法技巧，諸如題干重點詞下劃線、隱含條件的著重分析以及多情境的題干解讀等，使得學生掌握更多規范有效的問題題干解讀技巧，用于輔助個人后續規范化審題，進而實現科學規范分析數學問題題干要素內涵的目的.

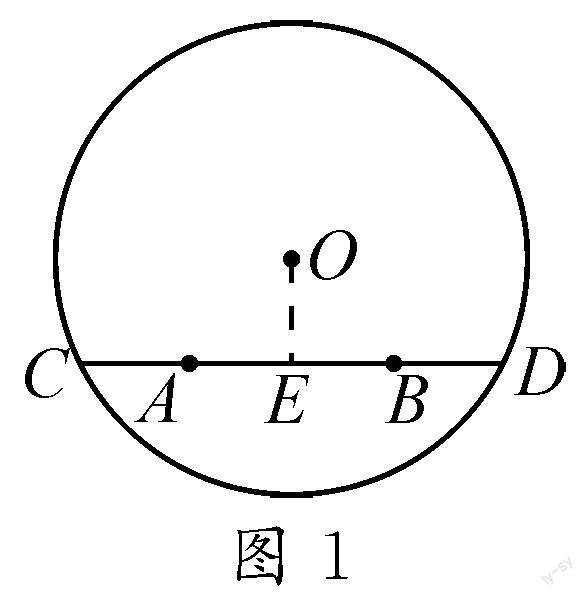
以“圓”的解題教學為例，呈現題目：已知線段AB在圓內，直線AB與圓O相交于C，D兩點，并且BD=AC，如圖1所示，那么OB=OA嗎？

為輔助學生更好地掌握本問題所考查的知識點以及題干核心，教師可著重引導學生運用規范審題技巧，先在條件“BD=AC”以及問題“OB=OA”兩個重要題干要素下畫上橫線.然后讓學生嘗試過圓心O作AB垂直OE于點E，進而可得DE=CE.而學生后續只需要結合上面規范化審題所圈畫的核心題干要素，便可發現因為“BD=AC”，所以可得BE=AE，證明OE為AB的中垂線，并根據圓的垂徑定理證明OB=OA.這樣，通過規范審題技巧的傳授，幫助學生精準掌握與“圓”有關問題題干的重點要素，輔助學生找到解決問題的方向，最終達到提升學生數學審題規范程度的目的.

2.2 規范解題步驟書寫，提升學生解題規范程度

科學規范的解題過程，不僅是學生思考數學問題流程的重現，也是學生數學答題素養的重要體現.但是，部分學生為了追求解題效率，大多會跳步或縮寫解題的流程，以更為簡便的形式書寫解題流程.如果在重要步驟或關鍵步驟處突然出現跳步或縮寫，那么批閱者可能弄不清解題的思路方向，因而造成解題失數.對此，初中數學教師解題規范化教學活動開展的第二步，便是要規范學生解題步驟的書寫，在精簡解題步驟的同時要避免重要步驟的省略，并做到科學使用規范的數學語言，邏輯嚴密地通過解題步驟展現解題思路，以此來提升教師對學生解題步驟規范性及科學性的認可程度，避免出現不必要的扣分現象.

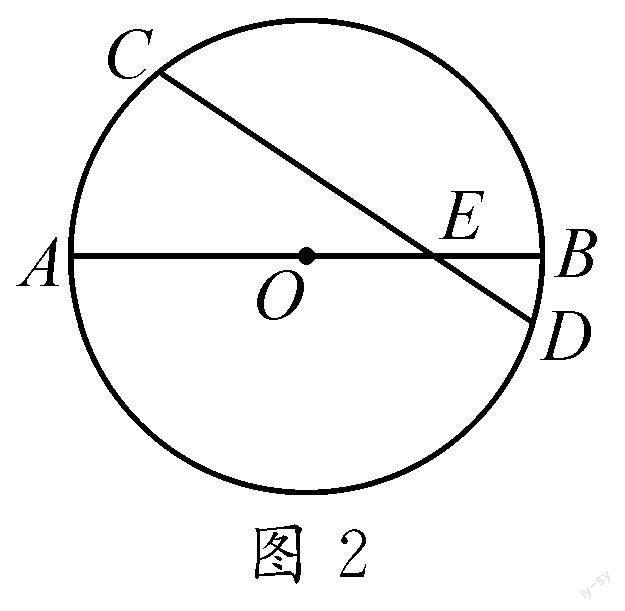
再如：在圓O中，已知弦CD和直徑AB相交于點E，∠CEA＝30°，如圖2所示，若EB=2 cm，AE=6 cm，請求出CD的長度.

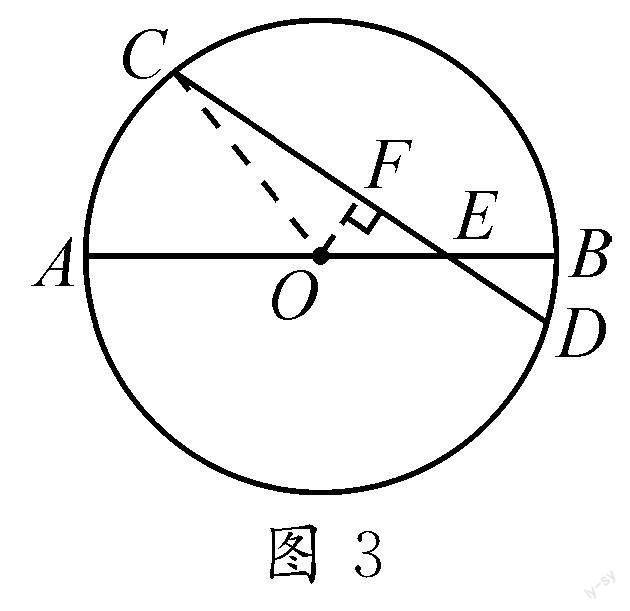
在本問題中，學生可通過構造一個以半弦、半徑以及弦心距為三邊的直角三角形，如圖3

所示，以求出本問題中的未知量.部分學生在完成過圓心O作CD垂直OF于點F，并連接CO后，會忽略“∵EB=2，AE=6”而直接得到“AB=8”，但這樣的解題步驟書寫并不規范.所以，教師應當嚴格要求學生按照如下步驟進行書寫：

過圓心O作CD垂直OF于點F，并連接CO.

∵EB=2，AE=6，

∴AB=8.

∴OA=4.

∵在Rt△OEF中，∠AEC=30°，

∵Rt△COF中，OF=1，OC=4，

∵CD⊥OF，

∴DF=CF.

這樣教師通過規范化解題步驟的演示，幫助學生了解到因果關系解題敘述不明確會失分，日常解題步驟書寫應當避免跳步情況的出現，盡可能按照解題思路進行規范化書寫，并精簡解題步驟，避免贅述情況的發生，最終達到顯著提升個人解題步驟書寫規范性的目的.

2.3 規范書寫解題結果，強化解題答案求算規范

解題答案的書寫作為解題規范化教學的最后一環，也是學生日常解題應當關注的重要對象.因為部分學生在完成規范化審題及解題步驟書寫后，容易出現懈怠心理，至使所求得的答案并非最簡，或者所得到的答案并不符合題干的要求，而這些都是數學解題答案不規范的重要表現.對此，為更好地建構一個科學完整的規范化解題流程，避免學生解題答案出現不規范的現象，教師應積極推進解題答案規范化工作的開展，結合題干的要求，進一步優化所得到的答案.同時，還應要求學生進行答案的二次檢驗處理，將答案代入到具體數學問題中進行演算求證，以保證所求得的答案真正符合題意.

以“圓”的解題規范化教學為例，教師可引入問題“以等腰三角形的一個腰為直徑的圓與底邊的交點平分底邊”，經過前面規范化審題、規范化解題步驟書寫的訓練，學生通過設AB，AC為等腰三角形的腰，并且AB為圓O的直徑，底邊BC與圓O交于點D，證明得到D為線段BC的中點，且AD為△ABC的高，AD垂直于BC，再根據等腰三角形三線合一的性質證明問題.而教師則需在學生完成問題的規范化步驟書寫后，要求學生嘗試利用“等腰三角形的三線合一性質”進行問題答案的二次求證，檢驗各個環節的證明步驟是否規范，以保障證明過程的科學性與規范性.這樣，教師也借此強化了學生的解題答案規范化思想意識，促使學生關注與重視日常數學解題答案的規范程度，確保所求得的數學問題答案最優、科學合規且符合題目要求，實現數學解題規范化教學的有效閉環，鞏固規范審題、規范解題步驟書寫的學習成果.

初中數學教師需要針對學生的解題能力發展訴求，通過規范審題、解題過程步驟規范以及解題結果規范等多環節規范化解題教學活動的開展，建構完整的數學規范化解題教學模型，引導學生養成規范化解題的良好習慣，顯著減少因解題不規范而造成的失分、丟分現象，最終達到提升解題效率的目的.