初中幾何問題中線段長度的求解技巧探究
盧曉雨

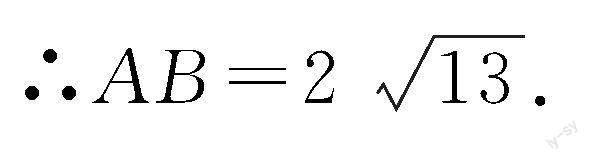
摘要:平面幾何是初中數學知識中重要的一部分,線段長度的變化影響著圖形的大小、形狀.考查線段長度的形式多種多樣,相關的問題也都十分靈活.求線段長度的基本方法有等面積法、利用勾股定理、利用相似等.本文中結合不同例題,具體分析解答求線段長度問題常見的解題思路.
關鍵詞:平面幾何;線段長度;解法思路
求線段的長度是初中幾何的基礎問題.解這類題目要綜合考慮線段的位置關系,通過題干信息的提取,采用合適的方式進行求解.
1 利用等面積法
等面積法是指用不同方式表示同一平面圖形的面積,通過面積的相互轉化或面積與邊、角關系的互相轉化,而使問題得到解決的方法.對于三角形而言,就是指利用三角形的面積自身相等的性質,或根據等高(底)的兩個三角形的面積之比等于對應底邊(對應高)的比等進行解題的一種方法.利用等面積法解題具有便捷、快速的特點.解題思路大致為:①根據已知條件通過面積的相互轉化或面積與邊、角關系的互相轉化,用不同方式表示同一三角形的面積;②通過題中已知條件進行運算即可求出所求線段長度[1].具體解題思路和步驟如以下例題所示.
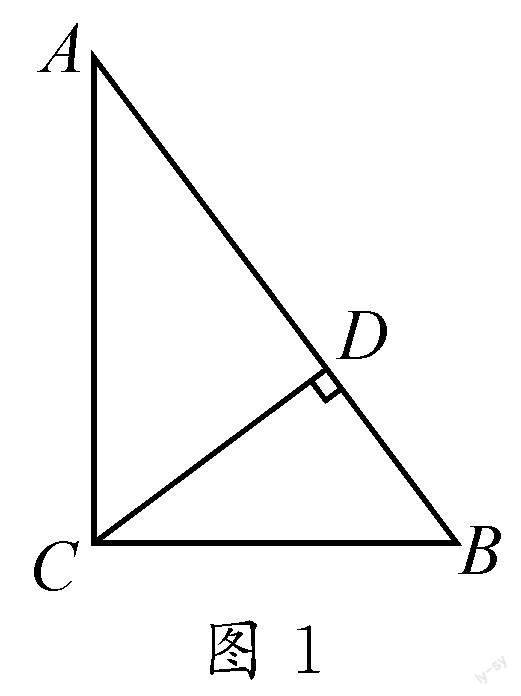
例1 如圖1,在Rt△ABC中,∠C=90°,AC=4,
BC=3,CD是斜邊AB上的高,求CD的長度.
分析:首先根據題中已知條件,可知在一個直角三角形中∠C=90°,以及AC和BC的長度,從而可求得AB的長,又根據CD是斜邊AB上的高,通過面積與邊、角關系的互相轉化,最后進行運算即可求出所求CD長度.
解:∵∠C=90°,
AC=4,
BC=3,
∴AB=5.
又CD為斜邊AB上的高,
∴S△ABC=AC·BC
=AB·CD.
∴4×3=5CD.
例2 如圖2,已知△ABC中,AD是△ABC的中線,AD=4,BC=6,AC=5,P是AB邊上的一點﹐且△PBD是以BP為底的等腰三角形,求線段AP的長度.
分析:首先根據題中已知條件,可得AD⊥BC.再根據面積相等可得DH長度.同理,可得BH長度.最后根據等腰三角形的“三線合一”性質,得到PH=HB,求出PB長度,從而求出線段AP長度.
解:過D作DH⊥AB,垂足為H.
∵AC2=AD2+CD2,
∴∠ADC=90°.
∴AD⊥BC.
在△ABD中,根據面積相等可得
在Rt△BDH中,求得
根據等腰三角形的“三線合一”性質,得
PH=HB,AB=AC=5.
2 利用勾股定理
已知直角三角形的兩直角邊長分別為a,b,斜邊長為c,則a2+b2=c2.因此,在直角三角形中,已知任意兩邊長,可求第三邊長.構造出直角三角形,用勾股定理建立方程求線段長度的解題思路大致為:①根據已知條件構造直角三角形;②利用勾股定理建立方程;③通過計算求出所求線段長度[2].具體解題思路和步驟如以下例題所示.
例3 如圖3,在Rt△ABC中,∠C=90°,AC=4,
BC=3,CD是斜邊AB上的高,求CD的長度.
分析:首先根據題中已知條件,可知在一個直角三角形中,∠C=90°,以及AC和BC的長度,從而可求得AB的長.再設BD=x,表示出AD.又因為CD是斜邊AB上的高,最后利用勾股定理建立方程,通過計算即可求出所求線段CD的長度.
解:∵∠C=90°,
AC=4,
BC=3,
∴AB=5.
設BD=x,
則AD=5-x.
∵CD為斜邊AB上的高,
∴在Rt△ADC與Rt△BDC中,有
CD2=AC2-AD2
=BC2-BD2.
∴42-(5-x)2=32-x2.
分析:首先根據題中已知條件,設CE=x,CD=y,再表示出AC和BC,最后利用勾股定理建立方程,通過計算即可求出所求線段AB的長度.
解:設CE=x,CD=y,
∴AC=2x,BC=2y.
∴在Rt△ACD與Rt△BCE中,有
(2x)2+y2=25,
(2y)2+x2=40.
∴x2+y2=13.
∴AB2=AC2+BC2
=4x2+4y2=52.
3 利用相似
利用相似求線段長度是根據邊角關系發現相似三角形的模型,從而通過運算得到所求線段長度.解題思路大致為:①根據已知條件構造出相似三角形;②設相應線段為x,建立方程;③通過計算即可求出所求線段長度.具體解題思路和步驟如以下例題所示.
例5 如圖5,Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN中,∠MPN=90°,點P在AC上,PM交AB于點E,PN交BC于點F,當PE=2PF時,求線段AP的長度.
解:如圖6,作PQ⊥AB于點Q,PR⊥BC于點R,則
∠PQB=∠QBR=∠BRP=90°.
∴四邊形PQBR是矩形.
∴∠QPR=90°=∠MPN.
∴∠QPE=∠RPF.
∴△QPE∽△RPF.
∴PQ=2PR=2BQ.
∵PQ∥BC,
∴AQ∶QP∶AP=AB∶BC∶AC
=3∶4∶5.
設PQ=4x,
則AQ=3x,AP=5x,BQ=2x.
∴2x+3x=3.
∴AP=5x=3.
根據上述不同的求線段長度例題的分析,可以得到求線段長度的基本方法有等面積法、利用勾股定理以及利用相似等.針對不同類型問題,采取相應的解題方法進行解答.在解題過程中,應加強對問題條件的分析應用,借助已知條件和相關性質去靈活解答,以此提高解題效率.同時,也希望同學們謹記各方法的注意事項,記住各方法的適用條件,在考試中靈活加以運用,避免出現錯誤.
參考文獻:
[1]程長賓.求線段長度最值的常用方法[J].初中數學教與學,2012(23):24-26.
[2]李丹.連結兩中點所得線段長度問題的求解策略[J].初中數學教與學,2017(17):23-25.

