變截面密封圈溫度場及密封性能分析*
鄒龍慶 陸信洲 祝 娟 俞 俊
(東北石油大學機械科學與工程學院 黑龍江大慶 163318)
變截面密封圈是一種基于流體動壓潤滑理論設計而成的旋轉動密封圈,主要特點是其具有規律性變化的波形潤滑邊界,當軸旋轉時潤滑油在波形潤滑邊界上形成垂直于邊界的速度分量,使潤滑油更易進入到動密封面間形成動壓油膜[1]。當動壓油膜壓力大于外界環境壓力時,會起到密封作用,所以變截面密封圈既實現了流體動壓密封,又避免了密封圈與軸的直接接觸產生摩擦磨損[2]。
國內學者對變截面密封圈的密封機制開展了研究并取得了一些研究成果。陳家慶等[3-4]分析了該種密封圈的密封特性,并給出其在石油機械中的應用,指出變截面密封圈可提供比普通密封圈更長久的使用壽命。鄒龍慶等[5]基于油膜厚度不變模型,推導出油膜厚度的近似計算公式。祝娟[6]研究了轉速、密封壓力和壓縮率等參數對變截面密封圈密封性能的影響。
上述研究工作都未考慮潤滑油溫度[7]和潤滑油剪切生熱[8]對密封性能[9]的影響作用。前人的研究[7,10-11]已經表明,密封圈與軸之間的溫度直接影響密封性能,嚴重時甚至改變密封效果。因此,本文作者以變截面密封圈潤滑油膜為研究對象,建立考慮黏溫特性的數值計算模型,采用FLUENT仿真分析軟件,研究轉速、密封壓力和潤滑油溫度與密封性能和溫度場[12]的關系,探究不同工況下變截面密封圈密封特性及潤滑油膜溫度場與黏溫特性的關系。
1 變截面密封圈潤滑油膜模型的建立及分析
1.1 潤滑油膜結構模型
參照Kalsi密封圈手冊[8]中的變截面密封圈截面形狀(見圖1)及結構參數(見表1),通過Solid Works軟件對所研究的變截面密封圈結構進行建模。

表1 變截面密封圈基本參數
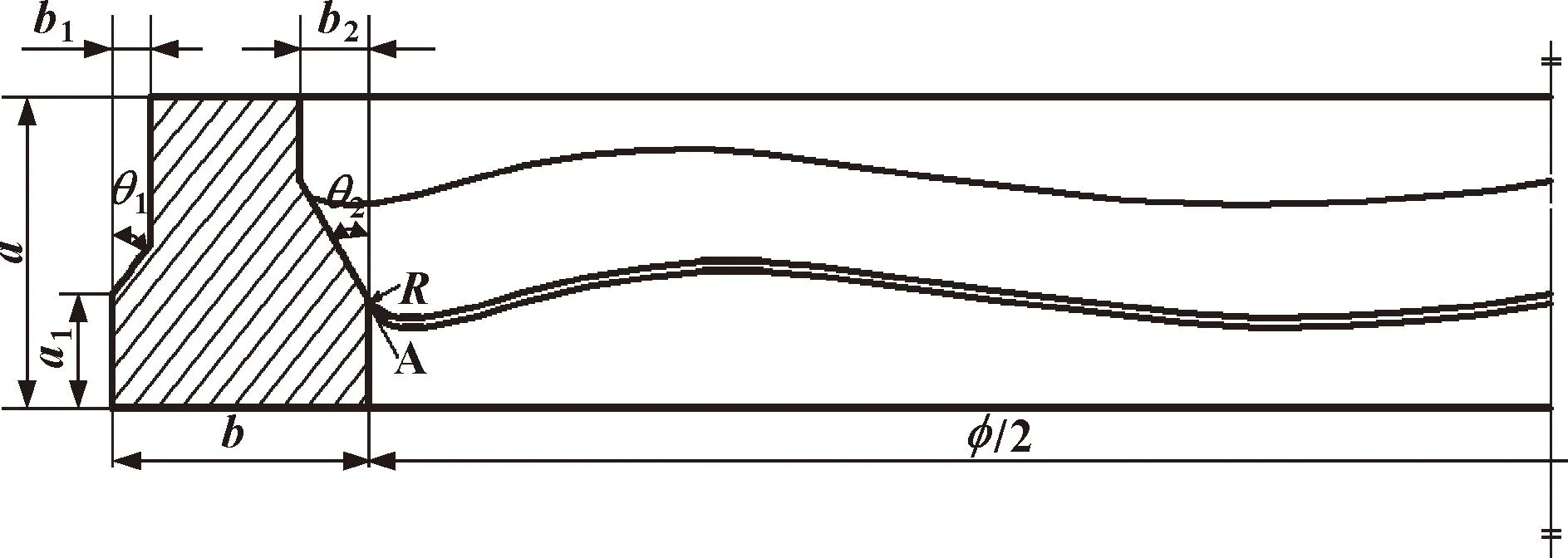
圖1 變截面密封圈截面形狀及幾何參數
圖1中點A位于密封面周向上,并隨波形潤滑邊界變化,目前對于該類密封圈的研究多數將波形潤滑邊界視為正弦曲線分布[6,13]。文中建立波數為6且波幅為1 mm的正弦潤滑邊界,點A坐標的變化規律滿足式(1),當t取0時,x、y和z為點A在正弦潤滑邊界原點處坐標(55,4,0)。
(1)
式中:x和z為密封圈徑向方向;y為密封圈軸向方向;t取值為0~2。
文中研究對象選擇為變截面密封圈穩定運行時,動密封面間的潤滑油膜部分,如圖2所示。應用ICEM提取內部流體域的方法,提取出變截面密封圈與轉軸中間的潤滑油膜部分進行分析。根據相關文獻[6]計算,穩定運行時油膜的平均厚度為30 μm,并且在文中選取的工況范圍內,變截面密封圈產生的變形量很小,并不會對油膜溫度場等結果造成顯著影響,所以文中不考慮變截面密封圈在不同工況下的變形對潤滑油膜流體域帶來的影響,故選取轉軸軸徑為54.97 mm。

圖2 提取潤滑油膜部分
1.2 潤滑油膜模型分析
1.2.1 模型網格劃分
將提取出的潤滑油膜流體域模型導入到ICEM中,由于六面體網格質量高[10],為提高收斂速度,潤滑油膜采用六面體單元結構網格,并根據所需邊界條件創建相應的Part,網格劃分結果如圖3所示,生成網格節點數為549 252,單元數為490 560。

圖3 模型網格劃分
1.2.2 基本參數設置
潤滑油膜流體域模型在Fluent中設置基本參數。動密封間隙中潤滑油的流動為層流,分析溫度對密封性能的影響,需要開啟能量方程,由于是潤滑油黏性內摩擦生熱[14],在能量方程中包含了黏性生熱Viscous Heating。潤滑油膜計算區域設置的邊界條件包括壓力入口、壓力出口、旋轉壁面轉速和溫度。
選擇的潤滑油為ISO320黏度的聚α-烯烴合成烴液體型潤滑劑,該類潤滑油與變截面密封圈HNBR材料有良好的兼容性。潤滑油的物性參數為:密度ρ=837 kg/m3,比熱容Cp=1 870 J/(K·kg),導熱系數λ=0.4 W/(m·K),動力黏度μ=0.2 Pa·s。分析選取潤滑油的溫度范圍為313~353 K,轉軸的轉速變化范圍為300~2 000 r/min,潤滑油的密封壓力范圍為2~7 MPa。
2 變截面密封圈的數值計算模型
根據變截面密封圈的結構及潤滑特點,Reynolds方程可簡化為
(2)
式中:x為周向方向;y為軸向方向;h為油膜厚度;μ為動力黏度;U為轉軸轉速;p為流體壓力。
考慮溫度的流體潤滑計算,必須將Reynolds方程和能量方程聯立求解[15]。文中針對潤滑油膜溫度場分布的模擬計算,提出以下假設:溫度、壓力和動力黏度沿膜厚方向不變化;密度與溫度無關。故能量方程可簡化為
(3)
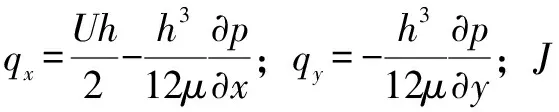
潤滑油黏度對溫度非常敏感[16-17],隨著潤滑油溫度升高,潤滑油黏度呈遞減趨勢。文中采用Barus方程對潤滑油的黏溫特性進行計算:
μ=μ0exp[-β(T-T0)]
(4)
式中:T0為初始溫度;μ0為溫度T0下的動力黏度;β為Barus黏溫系數。
采用有限差分法對雷諾方程和能量方程進行求解,并由式(4)更新潤滑油黏度,進而再次對潤滑油膜的壓力和溫度進行求解,運用MATLAB軟件進行迭代計算。通過比較仿真結果和數值計算得到的解析解,證明文中計算模型和結果的可靠性。
3 結果與分析
圖4所示是定黏度和變黏度2種情況下潤滑油膜的溫度場分布,選取軸轉速900 r/min,潤滑油溫度為313 K,密封壓力為5 MPa。可以看出定黏度和變黏度2種情況下的潤滑油膜溫度場均呈現周期分布,所以后期對潤滑油膜進行溫度場分析時,就可以選取一個周期區域進行分析。圖4(a)所示為定黏度時溫度場分布,可見最高溫度為364.8 K,較初始溫度增加了16.56%。圖4(b)所示為考慮黏溫特性得到的溫度場分布,可見油膜最高溫度為339.2 K,較初始溫度增加了8.38%。可以看出,2種情況下溫升相差2倍之多,并且考慮黏溫特性時油膜的最高溫度區域更大,所以對于變截面密封圈來說,潤滑油的黏溫特性是必須考慮的因素。

圖4 潤滑油膜的溫度場分布
3.1 轉速對溫度場及密封性能的影響
在潤滑油溫度為313 K,密封壓力為5 MPa工況下,分別計算了轉速為300、600、900、1 500、2 000 r/min時油膜溫度場分布,得到考慮黏溫特性時,潤滑油膜的溫度等值線分布如圖5所示。可以看出,隨著轉速的增大,潤滑油膜在軸向的溫度梯度增大,溫度值也隨之增大。因為變截面密封圈特殊的潤滑邊界,潤滑油膜的最高溫度位于外界環境側,向周圍逐漸減小;隨著轉速增大,潤滑油膜的最高溫度區域從潤滑邊界的原點處向波谷處移動,并且最高溫度區域逐漸擴大。
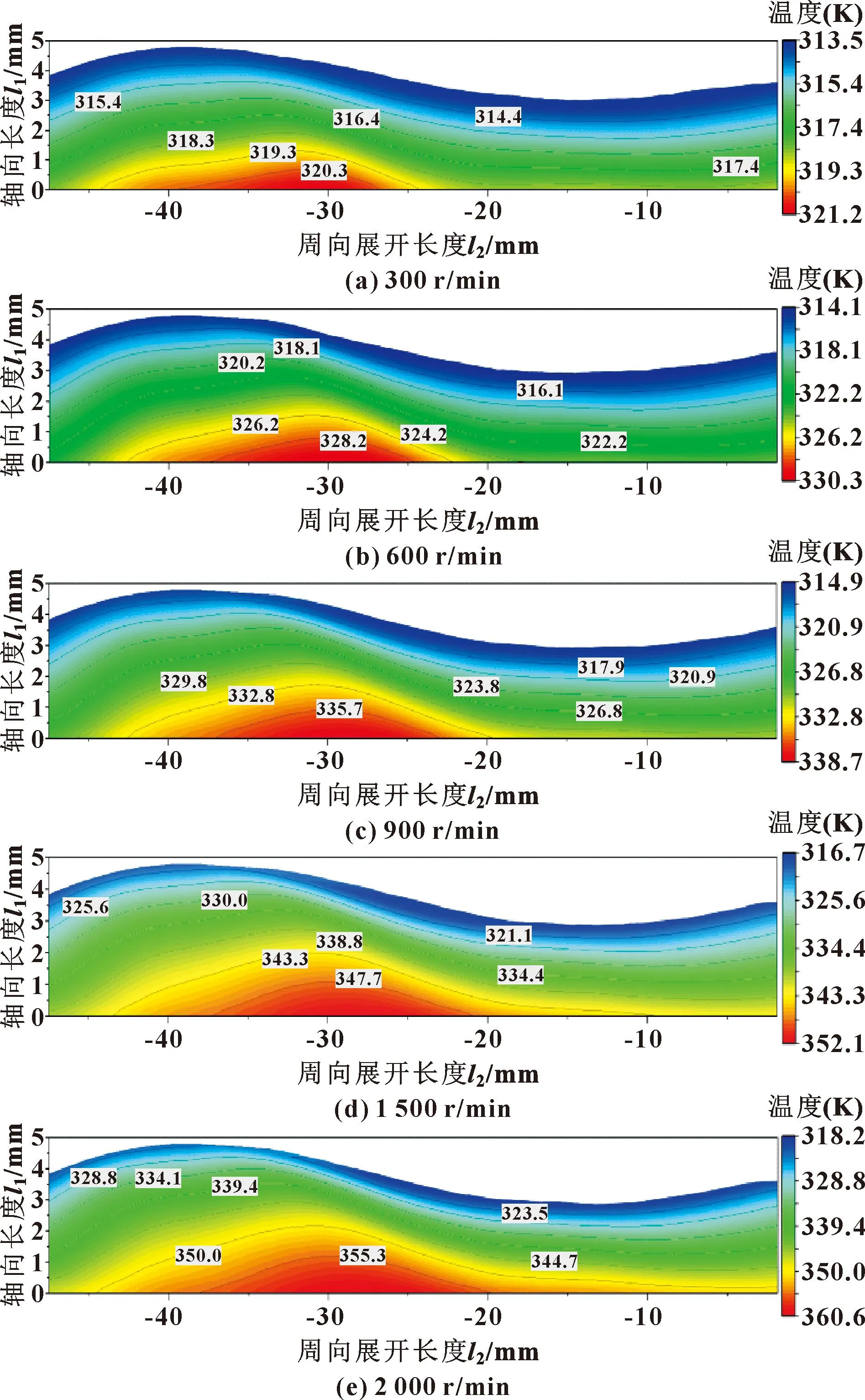
圖5 不同轉速下考慮黏溫特性的油膜溫度場分布
圖6所示為潤滑油膜最高溫度隨轉速的變化曲線。最高溫度隨轉速的增加而增大,由式(4)計算可知,潤滑油黏度隨溫度的升高而減小,因此定黏度時最高溫度的增長速度要遠快于考慮黏溫特性時的增長速度,并且相比于考慮黏溫特性時的最高溫度值,定黏度時的最高溫度值明顯偏高。在文中所選取的轉速范圍內,該類潤滑油可在考慮黏溫特性時穩定運行,而在定黏度時,轉軸的轉速應不高于1 500 r/min,當超過1 500 r/min后使用壽命會顯著降低。當其他條件恒定,轉速從300 r/min增加到2 000 r/min時,考慮黏溫特性時的最高溫度從321.4 K增長到360.9 K,增加了12.28%;而定黏度時的最高溫度從322.8 K增長到508.6 K,增加了57.54%,當轉速超過1 500 r/min之后,潤滑油最高溫度已超出其適用溫度。2種情況下所得到的溫度增長相差5倍之多,所以對于變截面密封圈的研究,必須考慮黏溫特性的影響。從圖中還可以看出,數值計算的解析解與仿真計算結果隨轉速的變化趨勢相同,并且兩者之間的誤差低于5%,從而證明文中結果的準確性和可靠性。

圖6 最高溫度隨轉速變化
泄漏量隨轉速的變化關系如圖7所示。油膜的泄漏量隨轉速的增大而增加,并且數值計算的解析解與仿真結果的變化趨勢相同,兩者之間的誤差處于5%以內。當轉速從300 r/min增加到2 000 r/min,定黏度時的泄漏量較原來增加了0.29%;而考慮黏溫特性時的泄漏量增加了93.78%。這表明當其他條件不變,隨轉速上升考慮黏溫特性時泄漏量的增速明顯快于定黏度時增速,并且考慮黏溫特性時泄漏量要遠大于定黏度時泄漏量,這是因為轉速增大后油膜溫度升高,潤滑油黏度隨之減小,流體動壓潤滑效應減弱,從而導致泄漏量的增加。這說明在變截面密封圈服役時,溫度對密封性能的影響是不可忽視的。
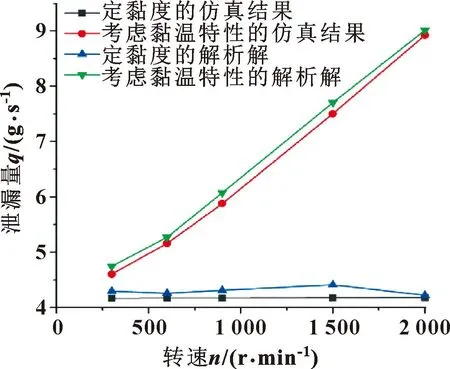
圖7 泄漏量隨轉速變化
3.2 密封壓力對溫度場及密封性能的影響
在潤滑油溫度為313 K,轉軸轉速為900 r/min工況下,分別計算了密封壓力為2、3、4、5、7 MPa時油膜溫度場分布,得到考慮黏溫特性時,潤滑油膜的溫度等值線分布如圖8所示。可以看出,因變截面密封圈特殊的潤滑邊界,潤滑油膜的最高溫度處于外界環境側,溫度向周圍逐漸減小。當密封壓力增大后,潤滑油膜溫度在軸向的溫度梯度減小,溫度值也隨之減小,潤滑油膜的最高溫度區域從潤滑邊界的波谷處向波峰處移動,并且最高溫度區域逐漸集中,最高溫度區域的集中會導致變截面密封圈的集中損傷。
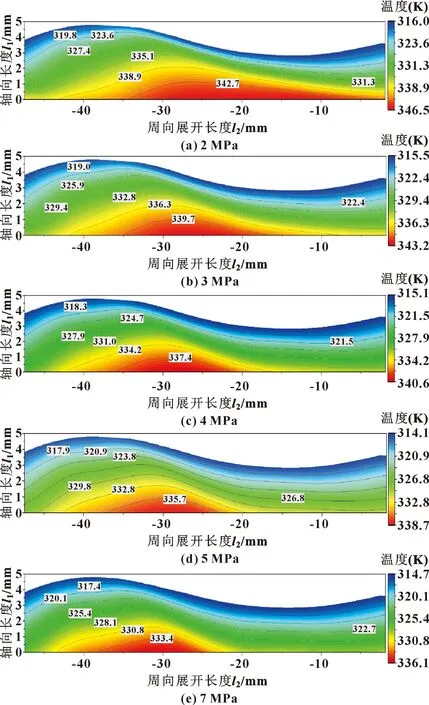
圖8 不同密封壓力下考慮黏溫特性的油膜溫度場分布
圖9所示為潤滑油膜最高溫度隨密封壓力的變化曲線。通過聯立迭代式(2)、式(3)和式(4),可得隨密封壓力增大,油膜最高溫度的解析解呈遞減趨勢,其與仿真結果基本保持一致,兩者的誤差處于1%~3%之間。當其他條件恒定時,密封壓力從2 MPa增加到7 MPa,考慮黏溫特性時的最高溫度減少了3.31%,并且考慮黏溫特性時的最高溫度值要低于定黏度時的最高溫度值;而定黏度時的最高溫度減少了23.01%,尤其是當密封壓力從2 MPa增加到3 MPa,最高溫度從461.5 K顯著降低到384.9 K,而高于3 MPa后,下降趨于平緩,但總體下降速度要快于考慮黏溫特性時的速度。說明因為油膜溫度升高,潤滑油的黏度降低,進而影響到油膜最高溫度。因此在文中選取的密封壓力范圍內,該類潤滑油在考慮黏溫特性時可以保證良好性能,在定黏度時密封壓力應選取高于3 MPa的工況,在密封壓力低于3 MPa時使用會嚴重縮減潤滑油以及變截面密封圈的使用壽命。
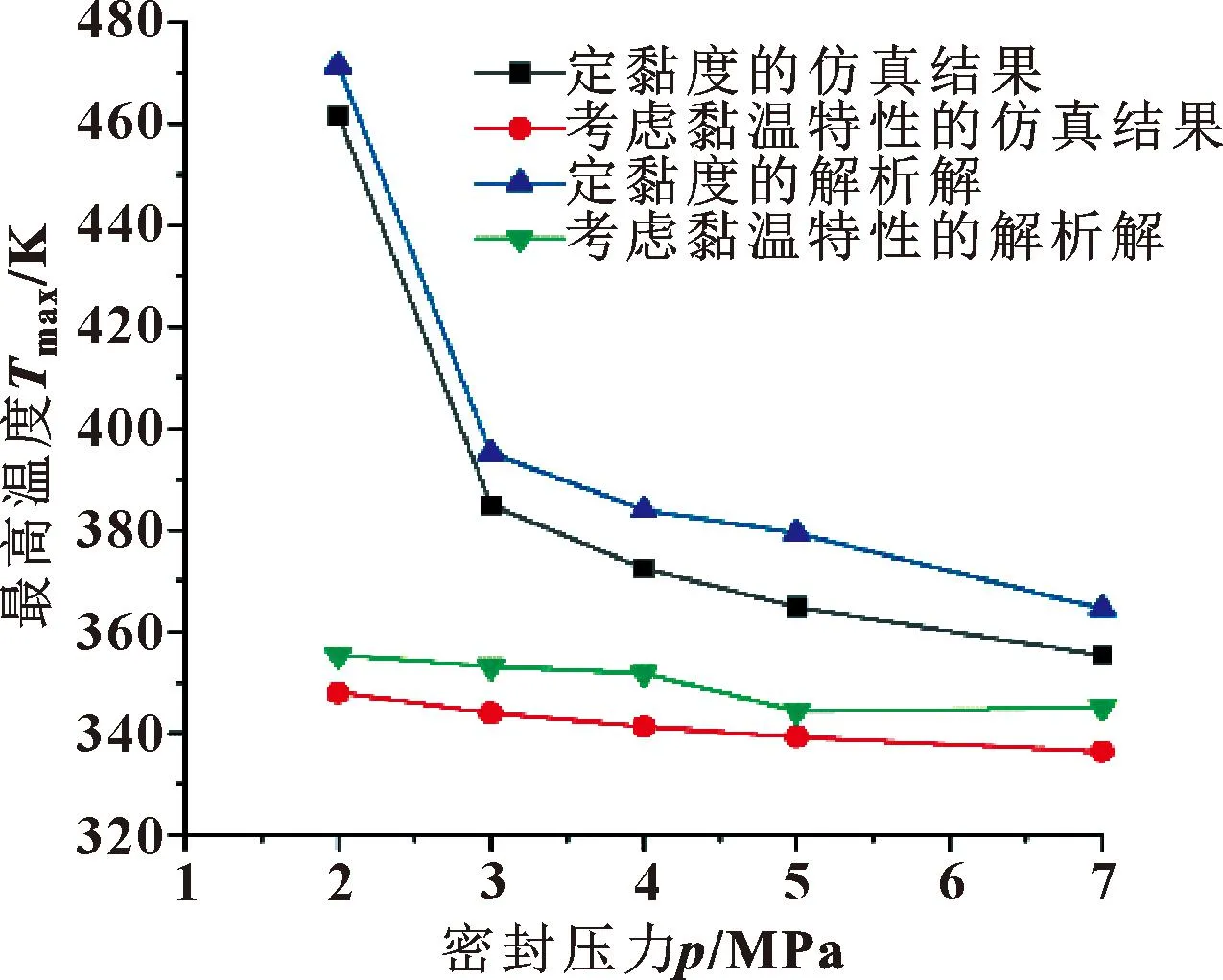
圖9 最高溫度隨密封壓力變化
圖10所示為泄漏量隨密封壓力的變化關系。當定黏度時,密封壓力從2 MPa增加到7 MPa,泄漏量增加了262.2%;而考慮黏溫特性時,泄漏量增加了183%,雖然定黏度時泄漏量的增長量大于考慮黏溫特性時的增長量,但相比于定黏度時的泄漏量,考慮黏溫特性的泄漏量要大于定黏度時的泄漏量。隨密封壓力增大,兩者的增長速度基本一致,均呈線性增長。這是因為密封壓力增大,流體動壓潤滑效應增大,泄漏量隨之變大,而考慮黏溫特性時,潤滑油黏度因溫升而降低,從而使得結果大于定黏度的結果。從圖中泄漏量變化曲線可看出,解析解和仿真結果變化趨勢相同,兩者之間誤差處于3%以內。
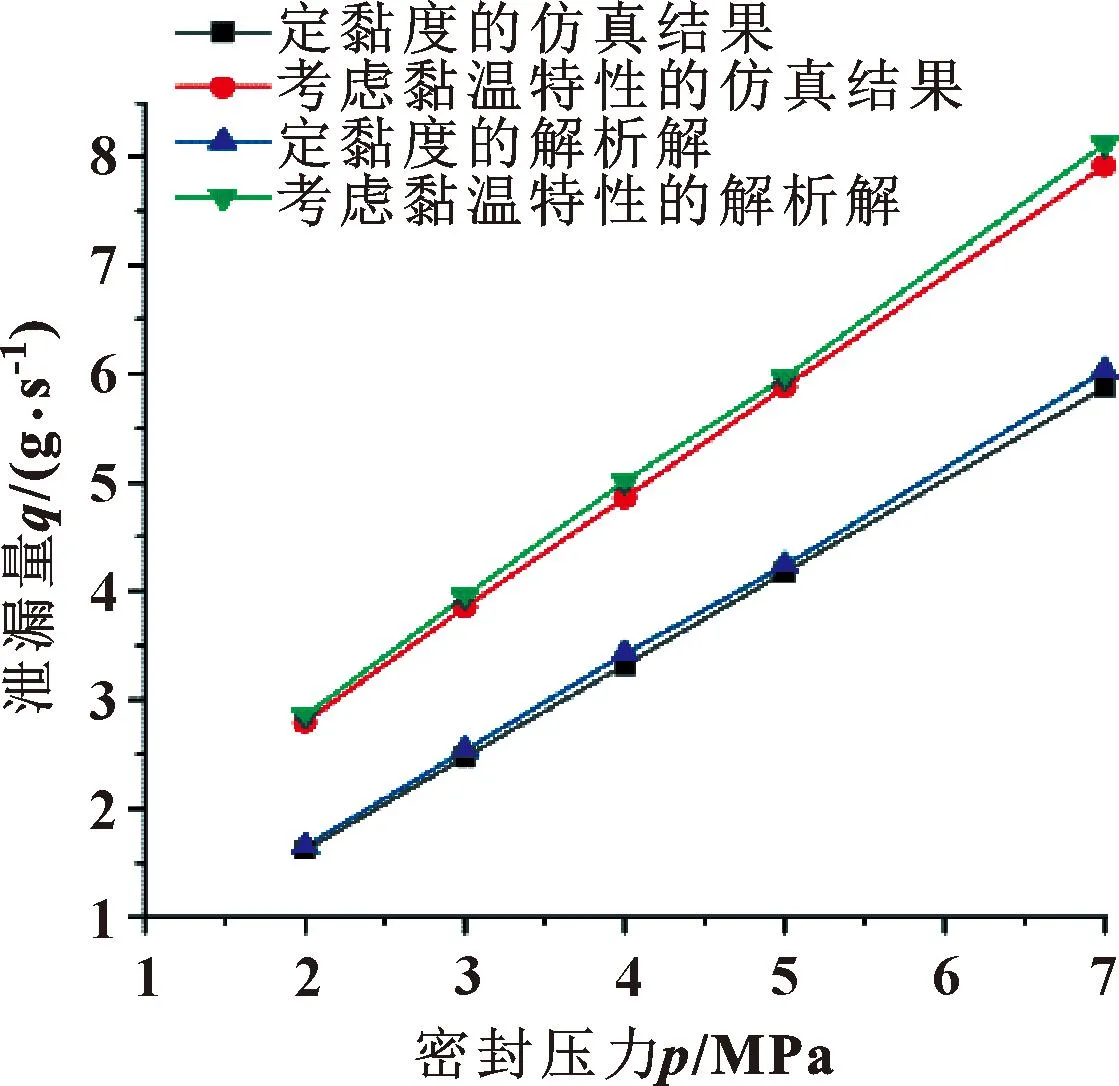
圖10 泄漏量隨密封壓力變化
3.3 潤滑油溫度對溫度場及密封性能的影響
轉軸轉速為900 r/min,密封壓力為5 MPa,分別計算了潤滑油溫度為313、323、333、343、353 K時油膜溫度場分布,得到考慮黏溫特性時,潤滑油膜的溫度等值線分布如圖11所示。可以看出,潤滑油膜的最高溫度區域同樣是分布在外界環境側。隨潤滑油溫度增加,潤滑油膜溫度呈遞增趨勢,最高溫度區域在軸向方向上逐漸縮小,并從潤滑邊界的原點處向波峰處移動。
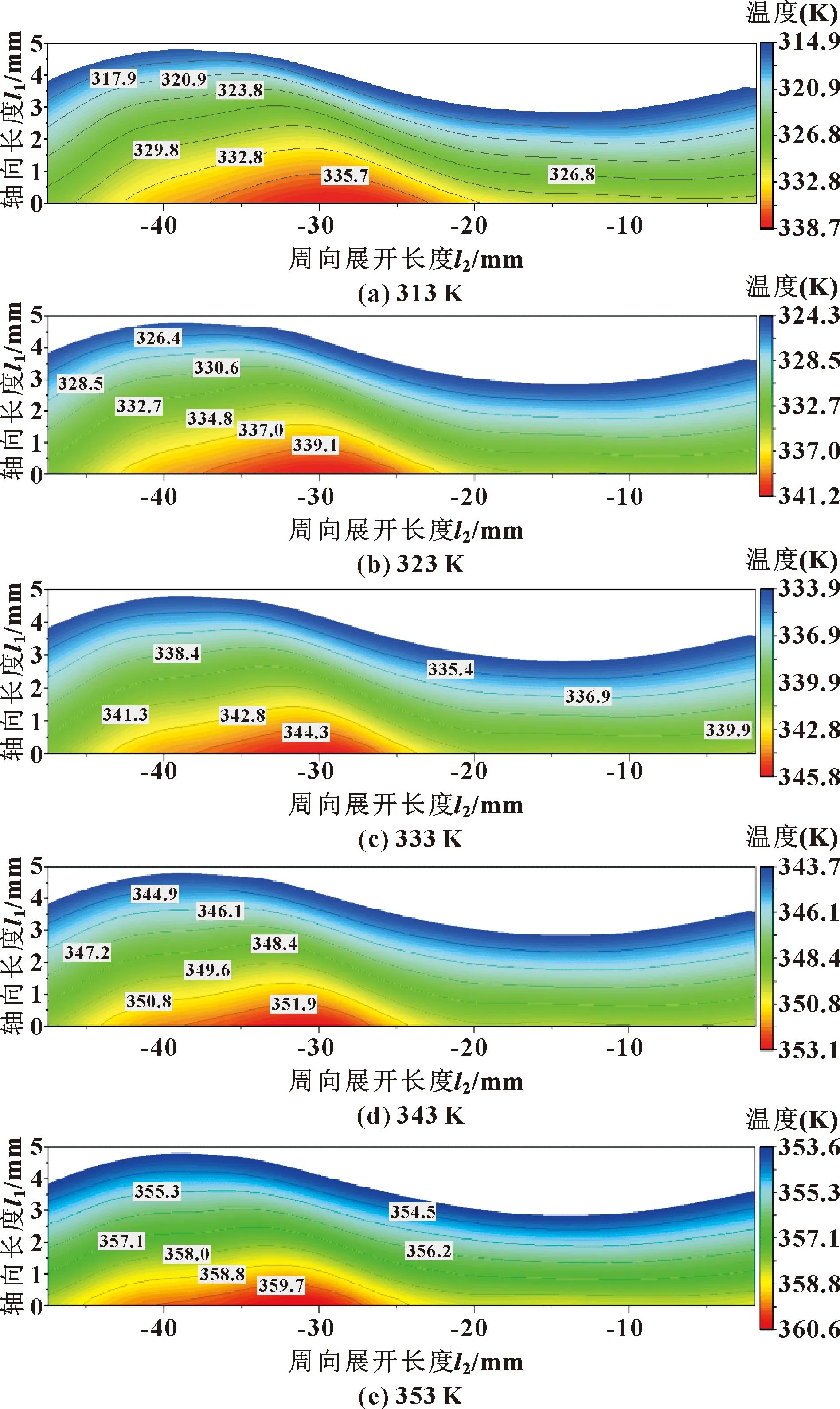
圖11 不同溫度下考慮黏溫特性的油膜溫度場分布
潤滑油黏度隨著潤滑油初始溫度的變化而改變,因此仍采用潤滑油溫度為313 K時的黏度來計算不同溫度時的結果是不準確的。為了提高計算的準確度,文中選取潤滑油在各溫度時的黏度作為初始黏度來進行計算。表2給出了不同溫度下潤滑油的黏度。

表2 不同溫度下潤滑油的黏度
圖12所示為油膜最高溫度和溫差隨潤滑油溫度的變化曲線。其他條件保持恒定時,隨著潤滑油溫度從313 K增加到353 K,定黏度時油膜最高溫度先從364.8 K減小到350.4 K,再增加到361.8 K,說明在定黏度時,如果希望油膜溫度保持在一個較低的水平,可將潤滑油的初始溫度選擇在333 K;當考慮黏溫特性時,由于潤滑油初始溫度和黏度不同,并且潤滑油黏度隨溫度的升高而減小,故油膜最高溫度隨潤滑油溫度增加而增加,增加了6.32%,但溫差均呈現遞減的趨勢,因此在文中選取的潤滑油溫度范圍內,當考慮黏溫特性時,油膜最高溫度均處于潤滑油的適用范圍內,可根據具體情況以及溫差變化規律,選取適合的初始溫度。油膜溫差如圖12(b)所示。由式(4)計算可知,潤滑油溫度升高,黏度下降,導致油膜溫差隨之減小,并且定黏度時的結果要大于考慮黏溫特性時的結果。由圖12(a)知,最高溫度的解析解要大于仿真結果,但兩者變化趨勢相同,且誤差均低于5%。
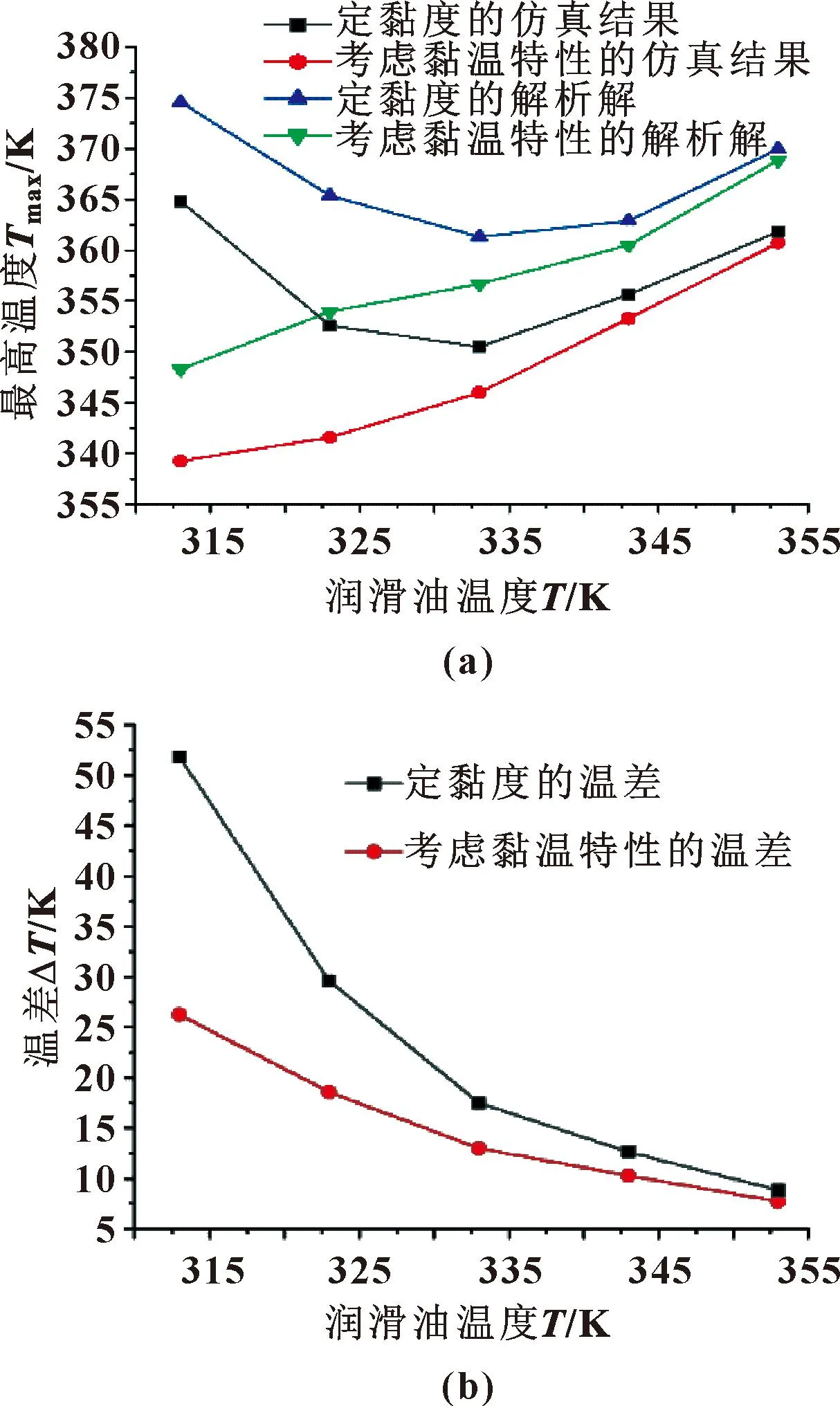
圖12 最高溫度(a)和溫差(b)隨潤滑油溫度變化
泄漏量隨潤滑油溫度的變化如圖13所示,當潤滑油溫度從313 K增加到353 K時,定黏度時的泄漏量增加了232.8%,考慮黏溫特性時的泄漏量增加了160.3%。因為考慮黏溫特性時潤滑油黏度會減小,流體動壓潤滑效應隨之減弱,導致考慮黏溫特性時的泄漏量大于定黏度時的泄漏量。從圖中變化曲線可看出,仿真結果和解析解在2種情況下的增長趨勢基本一致,并且兩者之間的誤差低于5%。
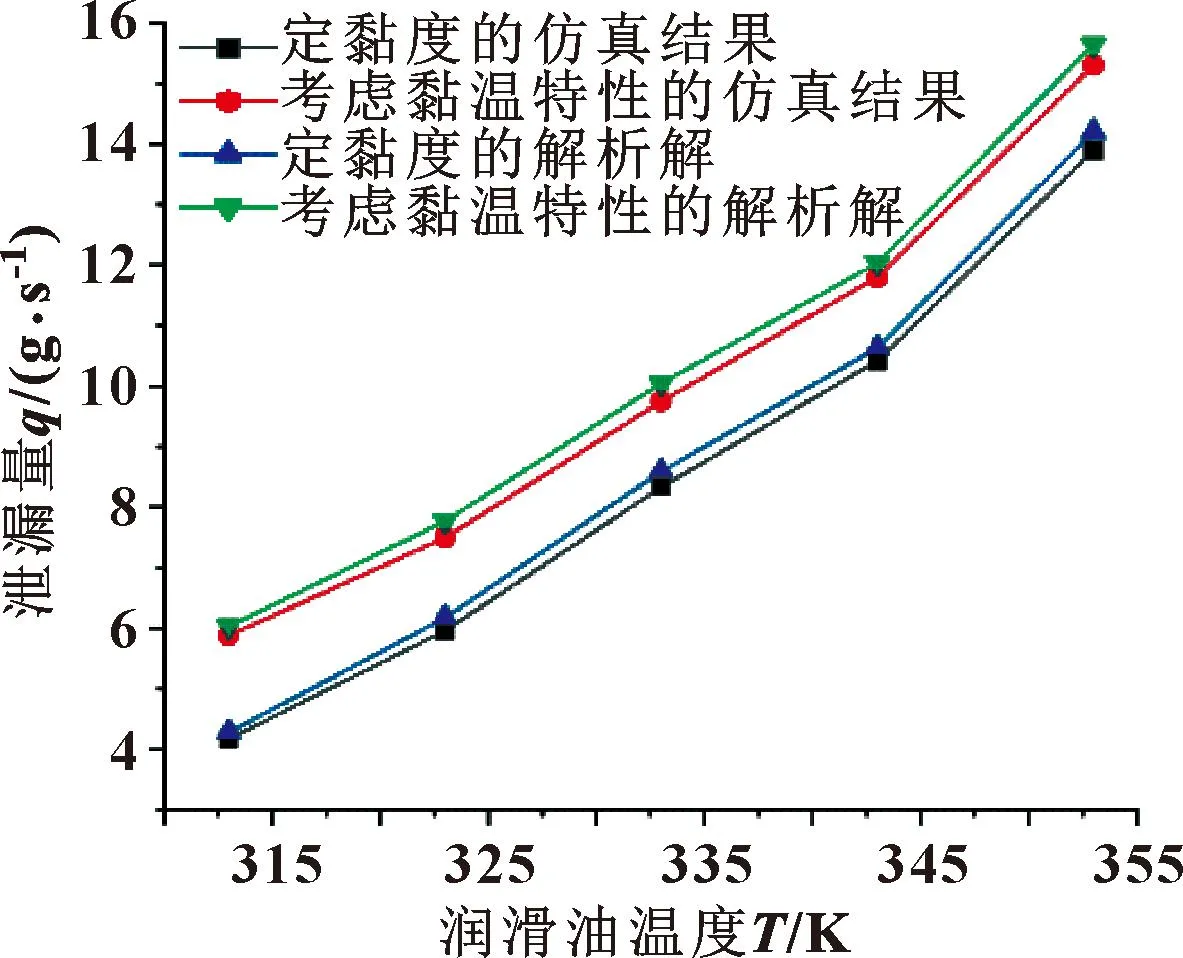
圖13 泄漏量隨潤滑油溫度變化
4 結論
(1)對于變截面密封圈,考慮黏溫特性和定黏度2種情況得到的溫度場、最高溫度和泄漏量3種性能差距顯著,因此,黏溫特性對密封性能的分析計算會產生重要的影響。
(2)隨著轉速增加,變截面密封圈油膜最高溫度區域逐漸變大,并從潤滑邊界的波峰處向著波谷處移動。潤滑油膜最高溫度值、泄漏量均隨轉速增加而增大,其中轉速對油膜最高溫度的影響大于其余工況。
(3)隨著密封壓力增大,油膜最高溫度區域逐漸集中,并從潤滑邊界的波谷處向著波峰處移動。最高溫度值隨密封壓力的增加而減小,定黏度時的下降速度更快。泄漏量隨密封壓力增大而增加,定黏度和考慮黏溫特性的增長趨勢基本一致。密封壓力對泄漏量的影響大于其他工況參數。
(4)隨著潤滑油溫度升高,油膜最高溫區域變小,并從潤滑邊界的原點處向波峰處移動。在定黏度時,最高溫度隨潤滑油溫度的升高呈先減后增的趨勢,當潤滑油溫度為333 K時,達到最小值;考慮黏溫特性時,最高溫度隨潤滑油溫度升高而增加,但溫差均呈遞減的趨勢。泄漏量隨潤滑油溫度的增加而增大。
(5)通過對比數值計算的解析解和仿真結果,可知兩者的變化趨勢保持一致,并且誤差均處于5%以內,從而證明文中結果的準確性和可靠性。

