圖形表征：培養(yǎng)學(xué)生數(shù)學(xué)運(yùn)算素養(yǎng)的有效途徑

陳姍姍

摘要：圖形表征所具有的直觀性使得其在表征數(shù)學(xué)對(duì)象中具有無可替代的優(yōu)勢(shì).因此，可以借助圖形表征，如實(shí)數(shù)軸、Venn圖、象限角和坐標(biāo)軸等，幫助學(xué)生明確運(yùn)算對(duì)象、掌握運(yùn)算法則、優(yōu)化運(yùn)算過程、設(shè)計(jì)運(yùn)算程序，從而正確求出運(yùn)算結(jié)果.

關(guān)鍵詞：圖形表征；數(shù)學(xué)運(yùn)算；集合

基金項(xiàng)目：廣東省教育科學(xué)規(guī)劃2022年度中小學(xué)教師教育科研能力提升計(jì)劃項(xiàng)目一般課題——基于數(shù)學(xué)表征的高中生運(yùn)算素養(yǎng)培養(yǎng)實(shí)踐研究（2022YQJK554）.

數(shù)學(xué)運(yùn)算素養(yǎng)的培養(yǎng)是一個(gè)常談常新的問題，更是讓師生頭疼的問題.影響學(xué)生數(shù)學(xué)運(yùn)算能力的因素有很多，且難以構(gòu)建行之有效的問題解決策略.圖形表征是指用具有一定結(jié)構(gòu)的直觀圖形（如小棒圖、數(shù)軸圖、線段圖等）表示數(shù)量或數(shù)量關(guān)系.由于圖形表征的直觀性，使得其在表征數(shù)學(xué)對(duì)象中具有無可替代的優(yōu)勢(shì).

集合知識(shí)在高中數(shù)學(xué)中屬于預(yù)備知識(shí)，雖然在教材中所占篇幅較少，但是在后續(xù)的學(xué)習(xí)中卻發(fā)揮了重要的作用.然而，部分學(xué)生卻在理解集合的概念、梳理集合間的基本關(guān)系，以及進(jìn)行集合的基本運(yùn)算時(shí)感到困難，這會(huì)影響學(xué)生之后的數(shù)學(xué)學(xué)習(xí).事實(shí)上，無論是集合的概念、集合間的基本關(guān)系，還是集合的交、并、補(bǔ)運(yùn)算，都可以轉(zhuǎn)化為圖形的形式進(jìn)行探究.例如，實(shí)數(shù)的集合可以用數(shù)軸呈現(xiàn)，點(diǎn)的集合可以用坐標(biāo)軸呈現(xiàn)，角的集合可以用象限角呈現(xiàn)，集合的交、并、補(bǔ)運(yùn)算則可以用Venn圖呈現(xiàn).通過圖形可以實(shí)現(xiàn)明確運(yùn)算對(duì)象、掌握運(yùn)算法則、優(yōu)化運(yùn)算過程、設(shè)計(jì)運(yùn)算程序的目的，從而促使學(xué)生快速、準(zhǔn)確地求出運(yùn)算結(jié)果.

一、實(shí)數(shù)軸：理解概念本質(zhì)，明確運(yùn)算對(duì)象

集合間的關(guān)系確定和集合運(yùn)算離不開數(shù)軸，但是剛進(jìn)入高中的學(xué)生用圖意識(shí)還不強(qiáng)烈，解題思維還停留在純粹的代數(shù)運(yùn)算上.高中階段數(shù)形結(jié)合思想的滲透最初就是從數(shù)軸開始的，而數(shù)軸的畫法也是所有圖形中最簡單的.從簡單的圖形入手，培養(yǎng)學(xué)生的識(shí)圖和作圖意識(shí)，是有效開展后續(xù)數(shù)學(xué)教學(xué)的重要保障.圖形所具有的直觀性是文字和符號(hào)無法替代的，尤其在新定義運(yùn)算中，陌生的表述會(huì)讓學(xué)生不知所措，不能理解概念，無法明確運(yùn)算對(duì)象，但是通過數(shù)形結(jié)合的方式則可以促進(jìn)學(xué)生對(duì)題意的有效理解.

由于實(shí)數(shù)與數(shù)軸上的點(diǎn)存在一一對(duì)應(yīng)關(guān)系，故數(shù)的問題可以轉(zhuǎn)化為數(shù)軸的問題進(jìn)行解決.利用數(shù)軸可以幫助學(xué)生清晰地理解新定義的符號(hào)的含義，明確運(yùn)算對(duì)象的本質(zhì).對(duì)于剛接觸高中數(shù)學(xué)的學(xué)生而言，數(shù)形結(jié)合主要體現(xiàn)在與數(shù)軸、Venn圖和二次函數(shù)的圖象有關(guān)的內(nèi)容上，教師在授課時(shí)要注意強(qiáng)化圖形的應(yīng)用，幫助學(xué)生掌握數(shù)形結(jié)合思想.

二、Venn圖：明晰求解目標(biāo)，掌握運(yùn)算法則

函數(shù)運(yùn)算、向量運(yùn)算或數(shù)列運(yùn)算都與加、減、乘、除四則運(yùn)算緊密相連，而集合運(yùn)算主要反映的是集合間的基本關(guān)系，這是集合運(yùn)算與其他運(yùn)算之間最大的區(qū)別.在一些復(fù)雜的集合情境中，學(xué)生很難利用列舉法或描述法解決問題.而借助Venn圖則可以清晰、直觀地表示集合間的關(guān)系，尤其對(duì)于集合間的交、并、補(bǔ)運(yùn)算，Venn圖更是展現(xiàn)了巨大的優(yōu)勢(shì).

例2某班45名學(xué)生參加植樹節(jié)活動(dòng)，每名學(xué)生都參加了除草、植樹兩項(xiàng)勞動(dòng).依據(jù)勞動(dòng)表現(xiàn)，將學(xué)生評(píng)定為“優(yōu)秀”“合格”2個(gè)等級(jí)，結(jié)果如表1所示.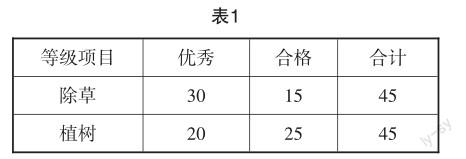

若在兩個(gè)項(xiàng)目中都被評(píng)定為“合格”的學(xué)生最多有10人，則在兩個(gè)項(xiàng)目中都被評(píng)定為“優(yōu)秀”的人數(shù)最多為（）.

（A）5（B）10（C）15（D）20

分析：此題的求解目標(biāo)是求在兩個(gè)項(xiàng)目中都被評(píng)定為“優(yōu)秀”的人數(shù)的最大值.與常規(guī)的集合運(yùn)算問題不同，這是一道求最值問題，較為少見.利用Venn圖可以清晰地表示在兩個(gè)項(xiàng)目中都被評(píng)定為“優(yōu)秀”的人數(shù)和在兩個(gè)項(xiàng)目中都被評(píng)定為“合格”的人數(shù)之間的關(guān)系，進(jìn)而有效解決問題.

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）》中對(duì)集合的基本運(yùn)算提出以下要求：（1）理解兩個(gè)集合的并集與交集的含義，能求兩個(gè)集合的并集與交集；（2）理解在給定集合中一個(gè)子集的補(bǔ)集的含義，能求給定子集的補(bǔ)集；（3）能使用Venn圖表達(dá)集合的基本關(guān)系與基本運(yùn)算，體會(huì)圖形對(duì)理解抽象概念的作用.由此不難看出，借助Venn圖解決集合運(yùn)算是學(xué)生應(yīng)該掌握的基本技能.借助Venn圖，學(xué)生能夠直觀理解集合間的基本關(guān)系，根據(jù)集合間的關(guān)系明晰求解目標(biāo)，進(jìn)而掌握集合的運(yùn)算法則.

三、象限角：避免分類討論，優(yōu)化運(yùn)算過程

解無定法，源于觀察.對(duì)于此題，也可以從代數(shù)運(yùn)算的角度進(jìn)行分析，此時(shí)則需要對(duì)k的取值進(jìn)行分類討論，進(jìn)而將集合N中的角的表示化成與集合M中的角的表示相近的形式.

分類討論是學(xué)生在高中數(shù)學(xué)學(xué)習(xí)過程中需要掌握的重要思想，也是學(xué)生理解的難點(diǎn).而對(duì)奇、偶數(shù)的分類討論更是一個(gè)難點(diǎn)，部分學(xué)生會(huì)出現(xiàn)理解上的困難.因此，要盡量避免分類討論，這是簡化數(shù)學(xué)運(yùn)算過程的一個(gè)重要途徑.既然是象限角，不妨利用坐標(biāo)軸畫出兩個(gè)集合所表示的角，集合M表示的角的終邊落在坐標(biāo)軸和第一、三象限的角平分線上（如圖3）；集合N表示的角的終邊落在坐標(biāo)軸以及第一、三象限和第二、四象限的角平分線上（如圖4），由此可以快速確定答案.

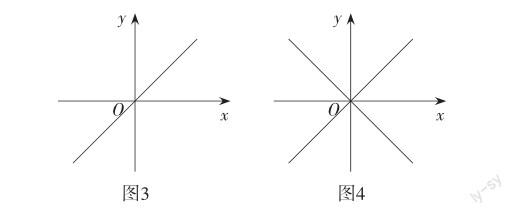
通過作圖分析，在避免分類討論的同時(shí)提高了解題效率，極大簡化了運(yùn)算過程.因此，教師在教學(xué)過程中要注意數(shù)形結(jié)合思想的滲透，強(qiáng)化學(xué)生的作圖意識(shí).

四、坐標(biāo)軸：轉(zhuǎn)換問題視角，設(shè)計(jì)運(yùn)算程序

以函數(shù)為載體的數(shù)學(xué)問題是教學(xué)中的重點(diǎn)也是難點(diǎn)，學(xué)生往往基于代數(shù)運(yùn)算的角度理解函數(shù)，而缺乏數(shù)形結(jié)合的轉(zhuǎn)換意識(shí)，尤其是對(duì)于比較抽象或復(fù)雜的運(yùn)算，如果僅從代數(shù)運(yùn)算的角度進(jìn)行求解，會(huì)出現(xiàn)較為復(fù)雜的運(yùn)算程序.因此，借助圖形表征轉(zhuǎn)換問題視角，不僅有利于提高運(yùn)算的正確率，而且有利于設(shè)計(jì)簡潔、科學(xué)的運(yùn)算程序.

根據(jù)題意，可知以原點(diǎn)為起點(diǎn)，以圖象上的點(diǎn)為終點(diǎn)的兩個(gè)向量互相垂直，簡單理解就是圖象上總能夠找到兩個(gè)以原點(diǎn)為起點(diǎn)的向量互相垂直，即以原點(diǎn)為起點(diǎn)且互相垂直的兩個(gè)向量的終點(diǎn)落在函數(shù)圖象上.而兩坐標(biāo)軸上的點(diǎn)剛好滿足以原點(diǎn)為起點(diǎn)，且互相垂直.因此，互相垂直的向量可以借助兩個(gè)坐標(biāo)軸呈現(xiàn)，然后旋轉(zhuǎn)兩個(gè)坐標(biāo)軸，探究兩個(gè)坐標(biāo)軸與圖象的交點(diǎn)情況.如果將兩個(gè)坐標(biāo)進(jìn)行旋轉(zhuǎn)，當(dāng)圖象上任意一點(diǎn)落在一個(gè)坐標(biāo)軸上時(shí)，一定有另外一個(gè)點(diǎn)落在另一個(gè)坐標(biāo)軸上，則說明圖象對(duì)應(yīng)的集合就是“互垂點(diǎn)集”.

故答案選BD.

經(jīng)過兩次轉(zhuǎn)化問題的視角，即先轉(zhuǎn)化為向量的垂直問題，再轉(zhuǎn)換為圖象與兩個(gè)坐標(biāo)軸交點(diǎn)的問題，將符號(hào)表征下的數(shù)學(xué)運(yùn)算問題轉(zhuǎn)化成了對(duì)函數(shù)圖象和兩個(gè)坐標(biāo)軸交點(diǎn)情況的判斷，優(yōu)化了運(yùn)算程序，同時(shí)加深了學(xué)生對(duì)新定義的理解.

五、結(jié)束語

章建躍教授認(rèn)為，數(shù)學(xué)運(yùn)算是有“技術(shù)成分”的，會(huì)算而且知道怎樣算更準(zhǔn)更快，這是運(yùn)算素養(yǎng)的基本要求.圖形表征的直觀性可以起到簡化數(shù)學(xué)運(yùn)算的效果，如實(shí)數(shù)軸、Venn圖、象限角和坐標(biāo)軸等，這些常見的數(shù)學(xué)圖形簡單易畫，如果靈活運(yùn)用則能幫助學(xué)生明確運(yùn)算對(duì)象、掌握運(yùn)算法則、優(yōu)化運(yùn)算過程、設(shè)計(jì)運(yùn)算程序，為培養(yǎng)學(xué)生的數(shù)學(xué)運(yùn)算素養(yǎng)奠定扎實(shí)的基礎(chǔ).

參考文獻(xiàn)：

[1]劉京莉，王倩，李佳，等.多元表征視域下揭示數(shù)學(xué)運(yùn)算本質(zhì)[J].中小學(xué)教師培訓(xùn)，2017（7）：63-66.

[2]中華人民共和國教育部.普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）[M].北京：人民教育出版社，2020.