“問題串”串起數學概念教學的探索路徑

明蕾

摘要：立足單元整體教學設計理念，探討在概念教學中如何在一般觀念的統領下以“問題串”引導學生發現問題、提出問題、分析問題和解決問題，以發展學生的探索性思維并提升學生解決問題的能力.

關鍵詞：關鍵能力；概念教學；單元教學設計；問題串；一般觀念

一、教學內容解析

“三角函數的概念”（第2課時）選自人教A版《普通高中教科書·數學》必修第一冊（以下統稱“教材”）第五章“三角函數”.教材對于三角函數概念的引入路徑為：從單位圓出發，利用單位圓上點的坐標定義三角函數，建立周期現象，然后再建立其與銳角三角函數的聯系.這種引入方式有利于學生更自然地以單位圓為基石抽象出三角函數的定義，進而借助單位圓的性質（特別是對稱性）獲得對三角函數研究內容的啟發.本節課的教學就是要不斷引導學生利用數形結合思想展開對三角函數的定義域、函數值的符號、誘導公式一的探究，同時為后續對同角三角函數基本關系及誘導公式二～五的探究作鋪墊，從而發展學生的直觀想象和數學抽象素養.

明確研究對象是開展后續一切學習活動的基礎.三角函數的研究對象是周期現象，研究任務是建立一個函數來描述周期現象的變量關系，通過研究函數的性質來發現周期現象的變化規律——性質.本節課先讓學生根據定義得出三角函數的定義域和函數值的符號規律，由于探究內容相對簡單，可以由學生獨立完成.而對于誘導公式一，其本質是函數值會重復出現，它是“單位圓上任意一點旋轉整數周就回到原來的位置”的代數表示，可以直接由三角函數的定義得到，不存在理解上的困難.關鍵是如何讓學生發現和提出問題，也就是要“讓學生想到哪里去”.因此，教學設計注重從研究方法的高度進行引導，通過一系列思考、問題和追問引導學生找到研究路徑.基于此，確定本節課的研究路徑為：明確研究對象—對應關系的特點分析—定義—性質.

二、教學目標解析

1.目標

（1）借助單位圓，理解并掌握三角函數的定義域及其在各象限的符號規律，熟悉數學的研究路徑，發展探究與發現的數學思維.

（2）結合單位圓的性質發現誘導公式一，了解三角函數的周期性，培養“數學的眼光”，提升推理論證能力，發展直觀想象和數學運算素養.

（3）熟練運用誘導公式一解決實際問題，即任意角三角函數的求值問題.

2.目標解析

達到以上教學目標的標志如下.

（1）能根據三角函數值在各象限的符號規律，準確判斷任意角在各象限的符號.

（2）能根據三角函數的定義和單位圓的對稱性，推導出誘導公式一.

（3）能熟練運用誘導公式一和特殊角的三角函數值求出任意角的三角函數值.

三、教學問題診斷分析

在三角函數的定義域和函數值的符號規律教學中，注意提醒學生當角的終邊與y軸重合時，終邊上點的橫坐標為0.因此，正切函數的定義域要剔除終邊與y軸重合的角.而對于三角函數值的符號，只要根據定義及單位圓上點的位置，就可以作出判斷.

在本節課的教學中，我們需要利用三角函數的定義來研究三角函數的性質，教學難點在于一些學生不習慣借助單位圓的性質來研究三角函數的性質，從聯系的觀點看問題的經驗不足，對“如何發現函數的性質”認識不充分.對此，教師可以先帶領學生閱讀教材，了解有關教學內容，再通過問題引導學生展開探究.

四、教學過程設計

環節1：課前回顧，引發思考.

【設計意圖】檢驗學生對三角函數定義的掌握和應用情況.引發學生對題目中出現的三角函數值的正、負號判斷及借助單位圓的特征進行性質分析等問題進行初步感知與思考，進而展開對三角函數性質的探索.

環節2：問題導學，性質探索.

引導語：我們前面學習了三角函數的定義，根據已有的函數學習經驗，接下來應該研究關于三角函數的哪些問題？

在一般觀念的引領下，學生容易想到定義域、圖象等研究內容，但較難聯想到借助單位圓探究三角函數的有關性質.對此，教師結合以下問題進行適當引導.

問題1：你能根據任意角的三角函數定義，確定正弦、余弦、正切三種函數在弧度制下的定義域嗎？填寫表1.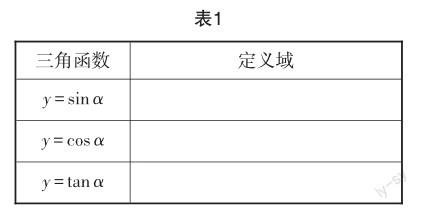

【設計意圖】學生熟悉一般觀念下的函數性質的討論方向，在此基礎上引導學生意識到三角函數與其他函數的不同之處，要借助單位圓來研究三角函數的性質，明確要研究的問題和思考方向.

追問：在明確三角函數的定義域后，應該繼續研究關于三角函數的哪些問題？

【設計意圖】由函數的學習經驗，學生容易提出值域、取值等研究問題，為三角函數值的符號問題的提出作好準備.

問題2：由三角函數的定義及任意角的終邊與單位圓交點所在象限，你能發現正弦、余弦、正切三種函數的值在各象限的符號規律嗎？填寫圖1中的括號內容，并用集合語言表示上述規律.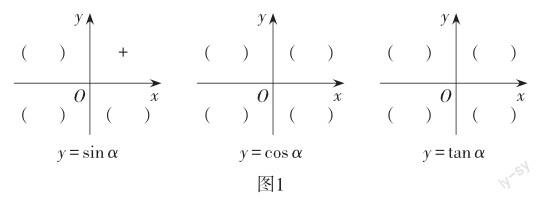

【設計意圖】讓學生了解三角函數值在各象限的符號，同時以單位圓為直觀工具，關注到三角函數的特殊性，為接下來的學習及誘導公式一的發現作準備.通過用集合語言表示三角函數的取值規律，復習了象限角、終邊相同的角的集合表示.

練習1：判斷正誤.

（1）已知α是三角形的內角，則必有sinα>0.

（2）若sinα>0，則α是第一象限角或第二象限角.

（3）對于任意的角α，sinα，cosα，tanα都有意義.

【設計意圖】讓學生利用新知解決問題，強化對三角函數值的符號規律的認識，以及對角的終邊位于坐標軸上這一特殊情況下三角函數取值規律的記憶，加深學生對知識的全面理解.特別地，練習3結合常用邏輯用語中的充要條件，以不等式組呈現問題，在問題求證過程中能夠有效培養學生的邏輯推理和抽象概括能力.

基于問題的求解，師生共同總結有關三角函數值符號問題的解題策略，具體如下.

（1）若已知角α的終邊所在的象限，則可以畫出單位圓，或利用“一全正，二正弦，三正切，四余弦”來解決角α的三角函數值的符號問題.

（2）若已知角α三個三角函數值中任意兩個的符號，則可以分別確定出角α終邊所在的可能位置，兩者的公共部分即為角α的終邊位置.

（3）對于多個三角函數值符號的判斷問題，需要進行分類討論.

【設計意圖】結合三角函數值的符號規律，確定具體三角函數的值.通過快問快答的形式，收獲學生的第一反應，引導學生初步感受“周而復始”，為誘導公式一的探究搭建橋梁.

問題3：前面結合三角函數的定義和單位圓上點的坐標或坐標比值研究了三角函數值的符號規律，而單位圓具有對稱性和“周而復始”的特性，反映到三角函數的取值規律上，就會呈現出更豐富的性質.有哪些特殊情況值得研究？

【設計意圖】引導學生關注單位圓的圖形特征，探究三角函數的特性，自主發現并提出接下來要研究的取值相等或相反、三個函數之間的關系等問題.

問題4：聯系三角函數的定義及終邊相同的角的表示，你能明確三角函數取值相等的條件嗎？

【設計意圖】引導學生從數與形兩個方面感受誘導公式一，基于圖形直觀感受“單位圓上任意一點旋轉整數周就回到原來的位置”，并總結出其“函數值重復出現”的代數表示，體會結合單位圓探索三角函數性質的優勢.

追問1：基于誘導公式一，你對三角函數的取值規律是否有進一步的發現？它反映了圓的什么特性？

追問2：誘導公式一有什么作用？

【設計意圖】通過兩個追問，啟發學生根據單位圓“周而復始”的特性，可以將任意角的三角函數值轉化為求0 ～ 2π內的角的三角函數值，為后續探索三角函數在整個定義域上的性質提供縮小研究范圍的思路.

練習5：判斷正誤.

（1）若α=β+720°，則cosβ=cosα.

（2）若sinα=sinβ，則α=β.

【設計意圖】利用誘導公式一解決問題，第（2）小題借助單位圓的對稱性情況，引導學生聯想更多性質.

練習6：利用誘導公式一確定三角函數值的符號，然后用計算器驗證.

【設計意圖】練習5借助誘導公式一和單位圓的對稱性情況判斷兩角關系，促進學生對誘導公式一的理解；練習6引導學生體驗單位圓方法與誘導公式一的有機融合；練習7利用特殊角的三角函數，進一步加深學生對誘導公式一的運用與理解.

師生共同總結利用誘導公式一化簡、求解三角函數的步驟，如圖2所示.

環節3：拓展思考，總結聯想.

問題5：誘導公式一表明終邊相同的角的三角函數值相等，那么具有對稱性的角的三角函數值之間又有什么聯系？正弦、余弦和正切的三角函數值都由角的終邊與單位圓的交點坐標唯一確定，它們之間又有什么內在聯系呢？總結本節課的研究過程，你能說說我們是從哪些角度入手發現三角函數的性質的嗎？你認為還可以從哪些方面入手研究三角函數的性質？

【設計意圖】帶領學生鞏固本節課所學的知識，并加深對知識的理解與掌握.引導學生自然地發現并提出有關具有對稱性的角的三角函數值的關系及其他誘導公式的問題，引出下節課所要學習的內容，培養學生探索與發現的數學精神.

（1）角θ為第二象限角的充要條件是__________；

（2）角θ為第三象限角的充要條件是__________.

【設計意圖】檢測學生對三角函數符號規律的掌握情況；鞏固學生對誘導公式一的應用及特殊角的三角函數值的記憶.

課后作業：教材習題5.2第1題、第3題、第4題、第5題、第7題、第8題、第9題、第10題.

五、教學反思

1.基于導向性，承載知識內核

本節課是學生探索三角函數有關性質的開始，需要深化學生對概念本質的理解，培養其對三角函數性質的探究能力，而非單純的理解接受能力.教師在教學中需要引導學生從三角函數的概念出發，逐步發現并提出三角函數的簡單性質.基于此，筆者通過層層遞進的“問題串”激發學生的探究興趣，帶領學生對問題進行逐步探究，同時注重基于一般觀念引導學生自主提出問題，以培養學生發現問題、提出問題、分析問題和解決問題的能力.

2.基于生成性，“四能”并重融合

對于“四能”的培養，要求教師在課堂教學中關注一般問題的分析與解決，同時引導學生生成三角函數的特性問題.本節課課前回顧中3道題目強調了單位圓在三角函數性質發現過程中的重要性，在此基礎上設計“問題串”為學生在本節課中的具體研究指明方向.需要注意的是，在提出問題后，要留給學生探索與發現的空間.合理的問題設計、有效的問題解決是學生問題探究能力生成的基礎保障.

3.基于時代性，促進教師成長

課程改革對教師在具體教學過程中落實立德樹人根本任務提出了更高的要求，除了要傳授知識外，更要注重對學生適應時代發展的思維品質與能力的培養.數學概念教學對教師專業能力的要求較高，不能單純根據知識點的多少來組織課堂.數學概念的抽象性、符號化、系統性決定了學習的難度，需要學生較高的能力來支撐.對此，教師需要不斷探索數學概念教學中蘊含的對學生核心素養和關鍵能力的培養策略.

思維品質與能力的培養不是一蹴而就的，問題驅動教學要貫穿在日常教學過程中.采用“問題串”教學，由淺入深地給學生提供思維提升的階梯，可以為學生的自主探究指明方向，從研究方法的高度引導學生發現并提出問題.好的“問題串”設計對教師的專業素養提出了較高要求.因此，“問題串”教學能有效促進教學相長，尤其在數學概念課的教學中值得推廣.

參考文獻：

[1]楊文，譚杰中，康健軍，等.基于問題串設計的概念教學：以“有理數的減法”為例[J].中學數學教學參考（下旬），2021（12）：5-7.

[2]章建躍.數學學科核心素養導向的“單元—課時”教學設計[J].中學數學教學參考（上旬），2020（5）：9-16.

[3]威金斯，麥克泰格.追求理解的教學設計[M].閆寒冰，宋雪蓮，賴平，譯.上海：華東師范大學出版社，2017.