借助數學實驗 促進深度學習

作者簡介：嚴劍調（1994—），本科學歷，中學二級教師，從事初中數學教學與研究工作.

[摘 要] 數學實驗是促進深度學習的“催化劑”.本文以“三角尺拼角”的實驗教學設計為例，具體從“操作思維是踐行深度學習的基礎”“合作探究是踐行深度學習的關鍵”“過程結果統一是踐行深度學習的核心”三方面談一些思考.

[關鍵詞] 數學實驗;深度學習;拼角

數學實驗在數學研究中并非占有主體地位，因為數學結論本身就具備確定性，課堂中不需要大量實驗進行驗證. 但從教學的角度出發，將數學實驗與深度學習有機地融合在一起，能發揮出實驗獨特的教育價值. 研究發現，若將動手操作與信息技術相結合進行數學實驗，往往能有效促進深度學習的發生.

實驗設計

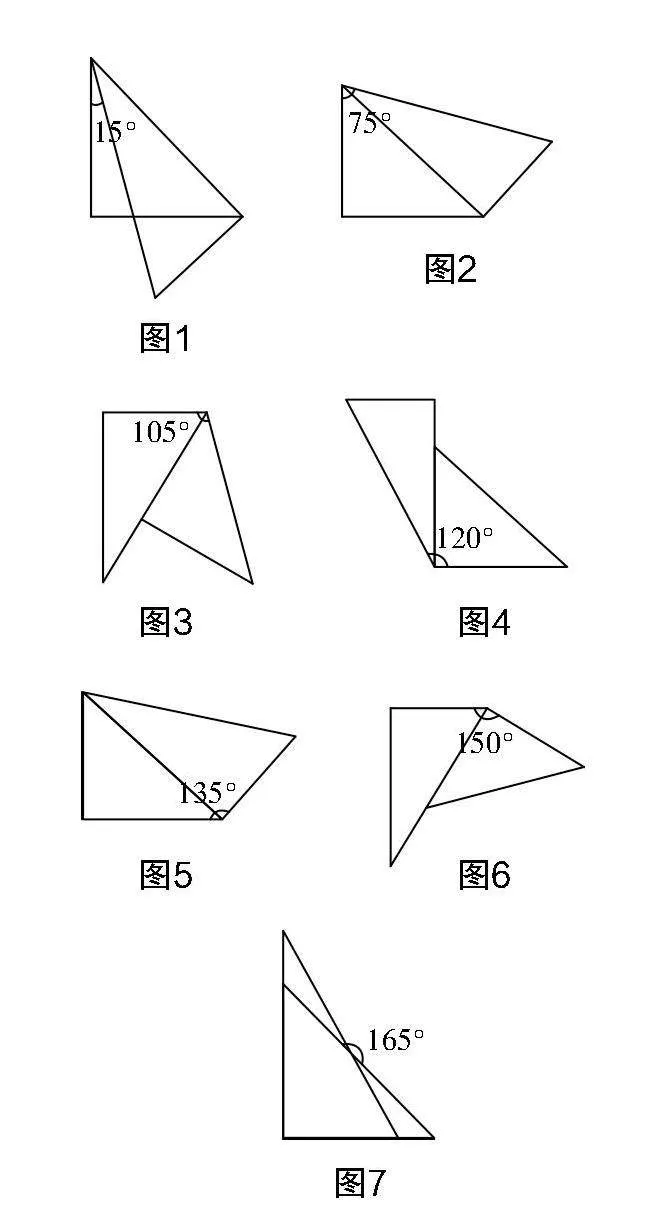
活動1 要求學生用一副三角尺進行拼角，同時思考以下幾個問題：①大家觀察手中的三角板，說說拼成的角度;②觀察拼角，可獲得什么結論？③以上觀察都是從“形”出發，若從“數”的角度思考，能獲得哪些角度？

借助多媒體展示學生的拼圖，如圖1～圖7所示.

設計意圖 從手動操作出發，學生通過層次清晰的活動產生探索欲. 學生觀察拼角，討論結論的過程，需通過小組合作學習的方式來完成，這是提升學生協作能力，促進深度學習的基礎. 第三個問題要求學生從“數”的角度思考拼角問題，希望學生通過動手、動腦對實驗進行觀察、猜想、總結等，以提升理性認識，促進深度學習的發生.

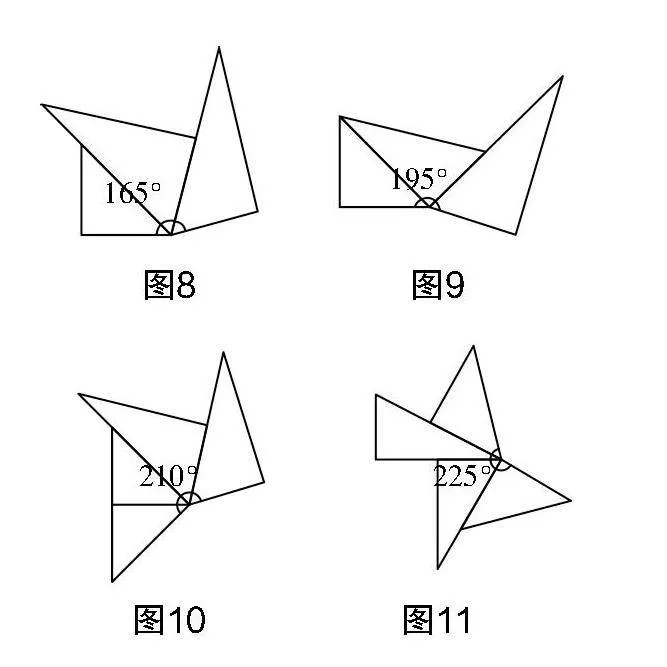
活動2 用兩副三角板拼角，同時思考以下幾個問題：①兩副三角板可以拼出哪些角？小組討論并介紹拼法;②能否拼出所有15°整倍數的角？③如果用更多三角板，能否拼出其他度數的角呢？

如圖8～圖11所示，借助多媒體展示部分學生用兩副三角板所拼成的圖形.

設計意圖 活動2進一步深化了學生對三角板拼角的認識，學生的思維從感性轉化到理解階層. 此活動設計意在訓練學生的觀察與分析能力，讓學生的思維從直觀形象轉化到抽象邏輯. 可視化的操作到抽象的數據分析，進一步提升了學生的深度學習能力，學生從中感悟到實驗背后所蘊含的方法與原理等，為后續利用模板拼角奠定了基礎.

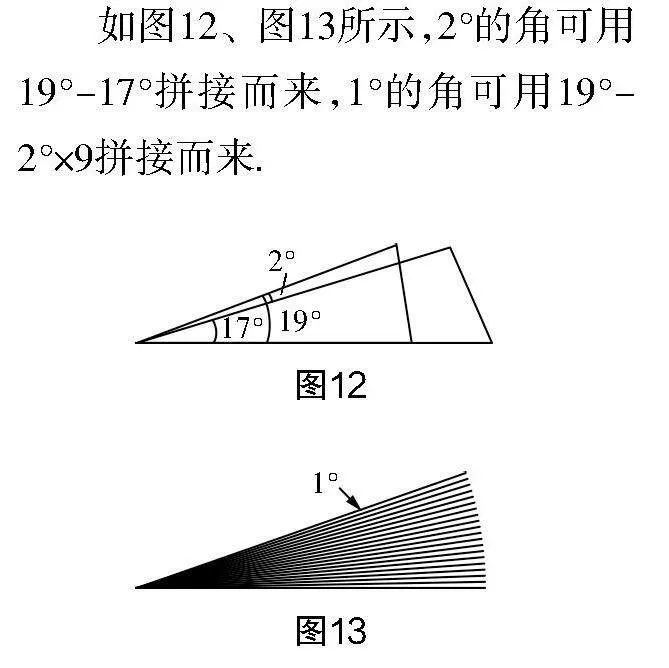
活動3 設計實驗模板，思考以下幾個問題：①若有17°與19°的模板，嘗試借助鉛筆與模板分別畫1°與2°的角，思考還能拼出哪些度數的角;②用17°與19°的模板是否可以拼出所有整度數的角？③嘗試自己設計模板進行拼角;④若設計出來的模板為a°與b°（a，b均為整數），可以畫出哪些角？

如圖12、圖13所示，2°的角可用19°-17°拼接而來，1°的角可用19°-2°×9拼接而來.

設計意圖 學生根據教師所提供的模板自主計算拼接出1°和2°的角，由此可確定任意整數度數的角都可以拼出來. 該實驗的目的意在讓學生經歷從特殊到一般的過程，讓學生發散思維，獲得歸納推理能力，從真正意義上踐行深度學習理念.

教學思考

1. 操作思維是踐行深度學習的基礎

傳統教學，教師更關注知識基礎的教學，要求學生掌握知識的結論，并利用所得結論解決實際問題，而對于學生動手操作能力的培養鮮少關注. 殊不知，數學理論的獲得往往來自實際操作. 想要踐行深度學習理念，首先就要擁有良好的數學操作思想，因為從真正意義上掌握教學內容絕非依靠單純的記憶或模仿，而應通過在實際操作的基礎上獲得直觀感知，讓學生對知識的認識實現從感性到理性的轉變，這也是學生獲取數學知識，形成良好應用能力的關鍵.

本節課，教師帶領學生從三角板拼角出發，讓學生通過自主操作來直觀感知拼角情況，進而啟發學生的操作思維，讓學生初步形成結論. 在此基礎上，提出用模板拼角的問題，使得學生再次通過操作進一步認識拼角過程與特點. 這種逐層遞進的實驗操作方式，使得學生從真正意義上體會到知識的形成與發展需經歷怎樣的一個流程，這對促進學生數學思維的發展具有重要意義，深度學習則在此操作中發生.

2. 合作探究是踐行深度學習的關鍵

數學實驗操作從本質上來看，屬于一種探究性活動，需要依靠學生的合作來完成一些任務. 學生邊操作、邊思考教師所提出的各個問題，在觀察與分析中探索知識特點. 因此，數學實驗一般會選擇具有開放性、挑戰性的主題，學生在富有探索價值的問題中操作，感知新課標所提倡的“自主探究、實踐操作與合作交流”相結合學習模式，并從中體驗團隊的力量，這是踐行深度學習理念的關鍵.

本節課的模板設計環節，教師鼓勵學生以小組合作學習的方式進行探討、交流、設計，并與學生積極互動，一起探索設計模板的方法，耐心傾聽學生的意見. 巡視過程中，筆者發現其中有一個小組設計出3°，5°以及8°的模板，模板設計沒有問題，但在思考這幾個模板可以拼接成怎樣的角度時出現了障礙.

為了順利解決這個障礙，教師鼓勵學生利用模板進行拼角. 操作中，學生自主發現可以獲得所有1°整倍數的角，大家因為得到這個結論而興奮，不知不覺中就達到深度學習的目的. 由此可以看出，在良好的情境中學習，學生在實驗操作與合作交流可不斷提升自身的認知水平，形成合作共同體，促進教學相長.

教師作為數學實驗的組織者與活動探索的引領者，應站到學生的角度來分析與思考問題，引導學生學會用數學的眼光、思維與語言來看待、思考與表達對這個世界的情感，讓學生在合作探究中取長補短、協同共進，感受數學學科獨有的魅力.

3. 過程結果統一是踐行深度學習的核心

在以中考為背景的情況下，不少教師為了提高升學率，過于追求學生對知識結果的掌握程度，片面地認為學生只要掌握了相關的結論，就能應用這些結論去解決問題. 事實上，數學結論的形成需要經歷一個過程，學生只有親歷其形成與發展過程，才能從真正意義上實現深度學習，這是培養與發展學生數學核心素養的關鍵一步.

斯托利亞認為：數學教學不僅僅是結論的教學，而是數學活動、思維的教學. 事實告訴我們，將數學過程與結果統一起來，才能促進學生形成終身可持續性發展的學習能力. 數學實驗就是將抽象的結論轉化為直觀可視的一種方式，即通過實驗操作探尋數學結論，讓學生在探索過程中發現知識背后隱藏的數學思想方法等，從而更加深刻地理解并掌握結論，為靈活應用夯實基礎.