解題探究:從“考題突破”到“教學微設”

作者簡介：王鑫（1990—），本科學歷，二級教師，從事初中數學教育教學工作.

[摘 要] 解題探究建議圍繞中考真題分兩個環節來構建：一是思路突破，解后總結;二是圍繞核心知識，開展教學微設計. 文章以2023年江蘇無錫的一道反比例函數中考題為例，探索問題解法及隱含模型，開展教學微設計.

[關鍵詞] 解題探索 ;“一線三直角”模型;教學微設計

由考題思路突破及模型探索

說起

考題 （2023年江蘇無錫中考卷第17題）已知曲線C，C分別是函數y=-（x<0），y=（k>0，x>0）的圖象，邊長為6的正三角形ABC的頂點A在y軸正半軸上，頂點B，C在x軸上（點B在點C的左側），現將△ABC繞原點O順時針旋轉，當點B在曲線C上時，點A恰好在曲線C上，則k的值為______.

思路突破 由條件可知，點A在y軸上，點B，C在x軸上，考慮到△ABC是等邊三角形，并且AO⊥BC，于是有∠BAO=30°. 所以tan∠BAO=tan30°==. 可按照如下步驟作圖：分別過A，B兩點作x軸的垂線，垂足分別為E，F，如圖1所示. 因為AO⊥BO，∠BFO=∠AEO=∠AOB=90°，所以∠BOF=90°-∠AOE=∠EAO. 于是有△BFO∽△OEA. 由相似性質，可得=

2=，又S==1，所以S=3. 最后結合反比例函數k的幾何意義，可得k=6.

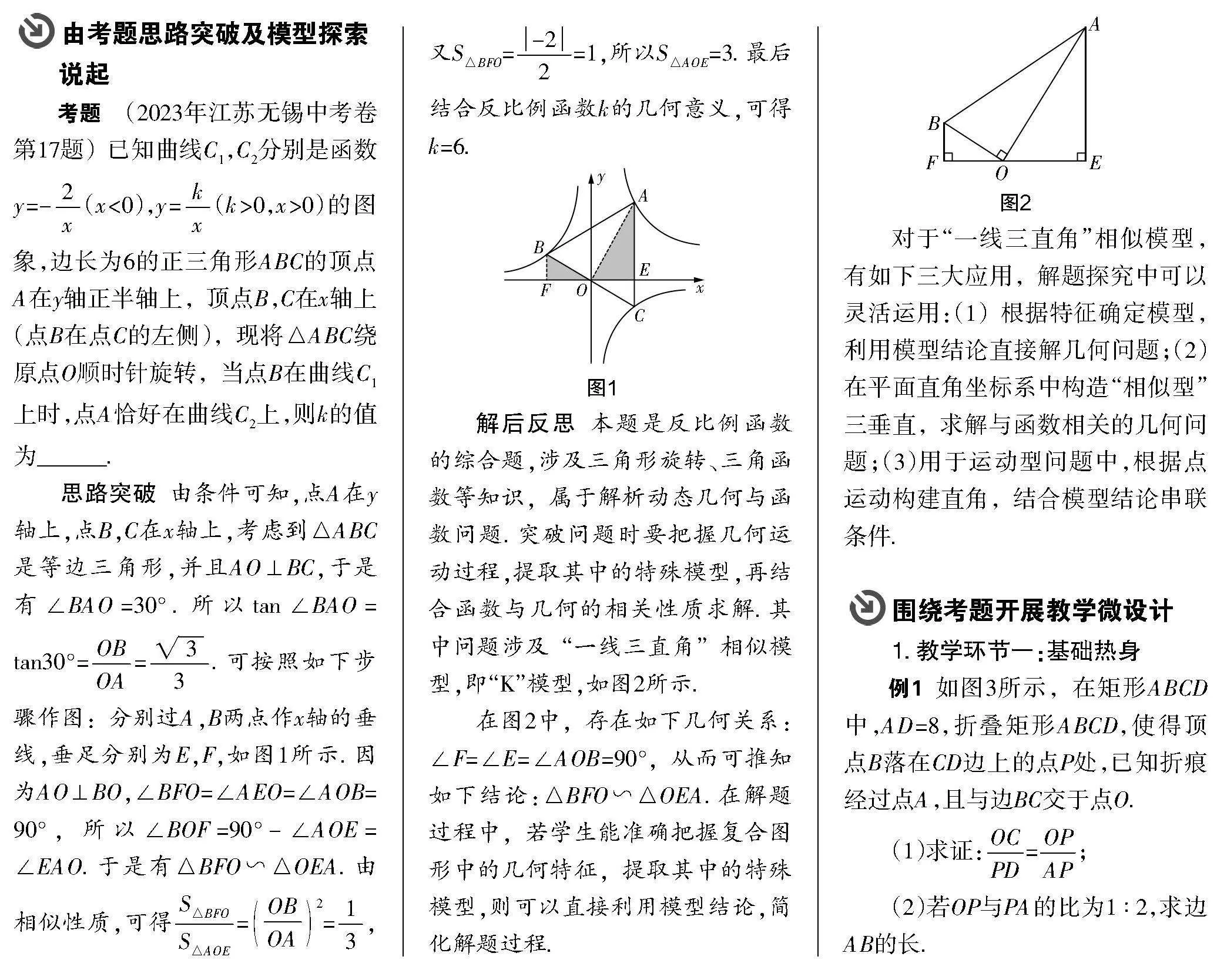
解后反思 本題是反比例函數的綜合題，涉及三角形旋轉、三角函數等知識，屬于解析動態幾何與函數問題. 突破問題時要把握幾何運動過程，提取其中的特殊模型，再結合函數與幾何的相關性質求解. 其中問題涉及“一線三直角”相似模型，即“K”模型，如圖2所示.

在圖2中，存在如下幾何關系：∠F=∠E=∠AOB=90°，從而可推知如下結論：△BFO∽△OEA. 在解題過程中，若學生能準確把握復合圖形中的幾何特征，提取其中的特殊模型，則可以直接利用模型結論，簡化解題過程.

對于“一線三直角”相似模型，有如下三大應用，解題探究中可以靈活運用：（1）根據特征確定模型，利用模型結論直接解幾何問題;（2）在平面直角坐標系中構造“相似型”三垂直，求解與函數相關的幾何問題;（3）用于運動型問題中，根據點運動構建直角，結合模型結論串聯條件.

圍繞考題開展教學微設計

1. 教學環節一：基礎熱身

例1 如圖3所示，在矩形ABCD中，AD=8，折疊矩形ABCD，使得頂點B落在CD邊上的點P處，已知折痕經過點A，且與邊BC交于點O.

（1）求證：=;

（2）若OP與PA的比為1 ∶ 2，求邊AB的長.

教學預設：選取上述幾何問題作為熱身探究素材，引導學生把握關鍵條件，結合折疊特性推導條件，根據問題條件來確定、提取模型，結合模型結論再逐步求解. 整體上按照“條件解析→模型提取→結論利用”的思路來引導.

（1）引導學生理解題意. “折疊矩形ABCD，使得頂點B落在CD邊上的點P處”，根據折疊特性可知△POA≌△BOA，從而可推得∠APO=∠ABO=90°. 綜合可得∠APO=∠D=∠C=90°，從而可提取其中的“一線三直角”相似模型，于是有△OCP∽△PDA，利用相似三角形的性質可得=.

（2）該問求線段的長，同樣需要充分利用模型結論進行推導. 根據“一線三直角”相似模型，可得△OCP∽△PDA，所以有=. 結合條件“OP與PA的比為1 ∶ 2，AD=8，可得=，所以PC=4. 在直角三角形中利用勾股定理構建方程求解：設AB=x，則DC=x，AP=x，PD=x-4. 在Rt△APD中，因為AP2=AD2+PD2，所以x2=82+（x-4）2，解得x=10，所以AB=10.

2. 教學環節二：拾0db2a095eb7743316a575cc8d8aee5bd0b0681ac49ba1dfe14d11f86d7189bc9級而上

例2 如圖4所示，在矩形ABCD中，E是對角線BD上一點，連接AE并延長交CD于點F，過點E作EG⊥AE交BC于點G. 若AB=8，AD=6，BG=2，則AE的長為（ ）

A. B.

C. D.

教學預設：本題為復合型幾何問題，具有一定的難度. 題目中沒有直接構建“一線三直角”相似模型，教學中教師可以引導學生分析問題條件，通過作輔助線來構建模型，再利用模型條件求解.

作圖建模：過點E作EN⊥BC，垂足為N，延長NE交AD于點M，如圖5所示.

條件推導：四邊形AMNB是矩形，故∠AMN=90°，AB=MN= 8，AM=BN，MN∥AB. 從而可證△DME∽△DAB，所以有=.

設定線段：設ME=x，則EN=MN-ME=8-x. 所以=. 所以DM=x，BN=AM=AD-DM=6-x，GN=BN-BG=4-x.

模型分析：由條件知∠AME=∠GNE=∠AEG=90°，顯然存在“一線三直角”相似模型，于是有△AME∽△ENG，所以有=，即=，解得x=，x=8. 經檢驗，x=，x=8都是原方程的根，但x=8不符合題意，舍去. 所以ME=，AM=6-x=. 由勾股定理可得AE===，故答案為B.

3. 教學環節三：深入拓展

對于其中的“一線三直角”相似模型，若存在一組對應邊相等，則可以生成特殊的“一線三直角”全等模型，如圖6所示. 教學中教師可以先展示模型，再預設問題探究.

在圖6中，存在如下幾何關系：∠F=∠E=∠AOB=90°，FO=AE，于是可推得結論：△BFO≌△OEA.

例3 如圖7所示，在△PMN中，PM=PN，PM⊥PN，P（0，2），N（2，-2），則點M的坐標是（ ）

A. （-2，0） B. （-2，0）

C.（-2，0） D.（-4，0）

教學預設：本題為“一線三直角”全等模型問題，其特殊之處在于引入了平面直角坐標系. 教學探究中教師需要引導學生探索模型成立的兩大條件：一是等直角，二是對應邊相等，然后在此基礎上提取模型，利用模型推導線段長.

線段推導：過點N作y軸的垂線，垂足為D，如圖7所示. 已知P（0，2），N（2，-2），則OP=2，OD=2，DN=2，從而可得PD=4.

模型提取：教師引導學生分析其中的角度與線段等量條件，則有∠MOP=∠MOD=∠PDN=90°，PM=PN，則有△MOP≌△PDN.

解題推導：根據模型結論有OM=PD=4，則點M的坐標為（-4，0），故答案為D.