基于舊知引出新

作者簡介:陳秀娟(1977—),本科學歷,中學一級教師,從事初中數學教學與研究工作.
[摘 要] 基于一次函數視角看二元一次方程(組)、一元一次方程、一元一次不等式是函數教學的重點和難點. 教學時教師可利用PPT將系列問題漸次呈現,通過對話、追問,引導學生從舊知過渡到新知,并學會自主歸納、概括新知. 此外,教師要特別重視數形結合思想的滲透,可以安排不同的學生上臺,結合圖形演示講解,以便診評學生對數形結合的理解和掌握情況.
[關鍵詞] 一次函數;一元一次方程;一元一次不等式;數形結合
寫在前面
蘇科版教材把“一次函數”安排在八年級上冊,而且是先安排一個課時單獨學習一次函數與二元一次方程之間的關系,后續課時才學習“一次函數、一元一次方程和一元一次不等式”(本文簡稱“三個一次”), 所以教師教學“三個一次”時,要充分考慮學生的“最近發展區”,要盡量從上一課已學內容出發,設計開課情境問題,然后引出本課要研究的內容.
“三個一次”新授課教學設計
教學環節1:復習舊知,引出新知
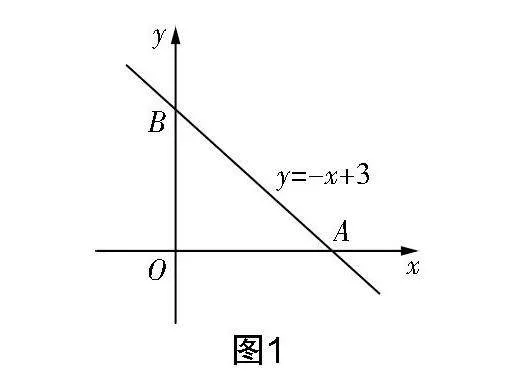
問題1:如圖1所示,在平面直角坐標系中,直線y=-x+3與x軸、y軸分別交于A,B兩點.
(1)自主設計一個問題,并在小組內說說你的設計意圖;
(2)畫出正比例函數y=2x的圖象,設其與直線y=-x+3交于點P,求點P的坐標;
(3)如圖2所示,設正比例函數y=kx(k>0)的圖象與直線y=-x+3交于點P(1,2),那么關于x的二元一次方程組kx-y=0,
x+y=3 的解是_______.
教學預設:“問題1”的各個小問以PPT形式漸次呈現. 實際教學時,教師還可以讓學生先畫出直線y=-x+3,再畫一個正比例函數的圖象,然后提出一個與一次函數有關的數學問題,并在小組內交流. 這個環節主要是讓學生復習舊知,因為舊知中蘊含著即將要重點學習的內容. 特別地,如果學生提到了一次函數圖象與坐標軸的交點,那么就為后續研究一元一次方程提供了引出情境.
這一環節,學生應該會想到很多問題. 當然,如果學生沒有想到一次函數與二元一次方程(組)相聯系的問題,教師可出示PPT展示一個相關問題.
教學環節2:探究新知,歸納概括
問題2:以一次函數y=-x+3為例,剛剛有同學研究了該函數的圖象與x軸公共點的問題,那如果不畫圖,能否心算出這個公共點的坐標?你是怎么算的?
教學預設:研究完這個特例問題后,教師可安排學生繼續思考一次函數y=2x+4的圖象與x軸公共點的橫坐標與方程2x+4=0的解之間的對應關系,進而推廣到研究一次函數y=kx+b與一元一次方程kx+b=0的關系. 最后,讓學生小結出一次函數圖象與x軸交點的橫坐標與對應一元一次方程的解之間的一般規律.
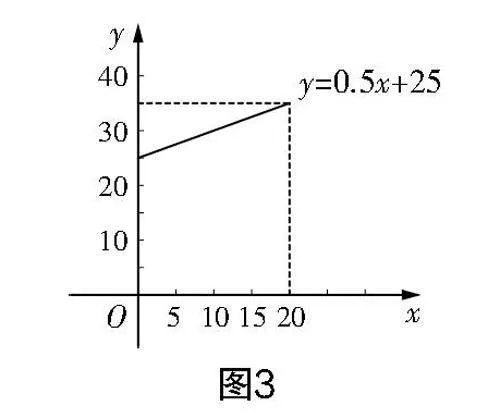
小結之后,教師可安排教材上一道體現一次函數與一元一次方程的例、習題,從而體現以課本為主線推進學程:一根彈簧的長度為y,所掛物體的質量為x,y與x之間的函數圖象如圖3所示,則當y=35時,該彈簧所掛物體的質量是多少?
教學環節3:繼續探究,成果擴大
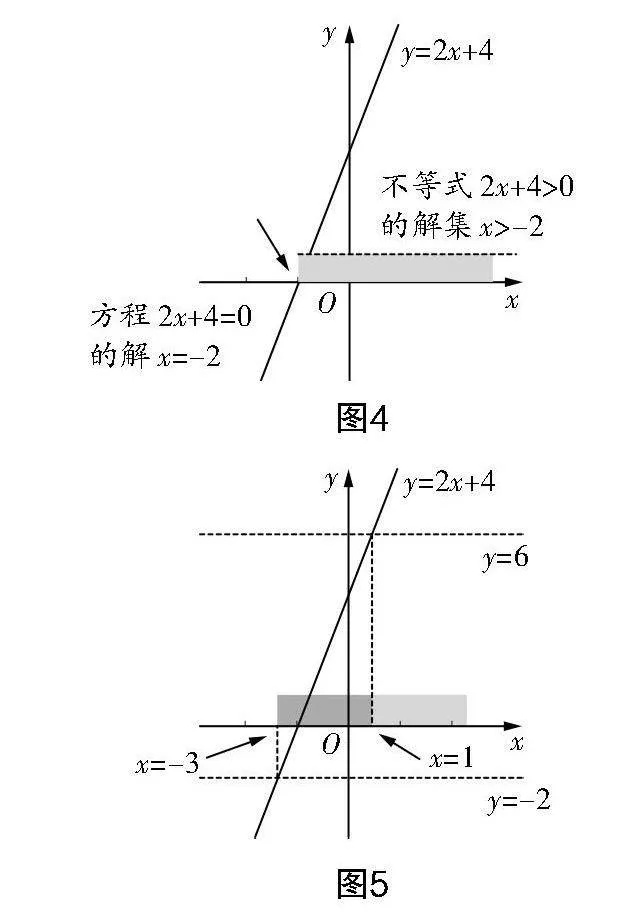
問題3:繼續研究直線y=2x+4,根據圖象,你能否直接說出不等式2x+4>0,2x+4<0的解集?
教學預設:安排學生結合圖4,以方程2x+4=0的解x=-2為基礎,得到結論“當x>-2時,y>0,即不等式2x+4>0的解集為x>-2;反之,2x+4<0的解集為x<-2”.
拓展追問1:從函數圖象的視角分析不等式2x+4≥6的解集.
拓展追問2:從函數圖象的視角分析不等式組-2≤2x+4≤6的解集.
教學預設:讓不同的學生結合圖5,數形結合地演示講解他們的理解. 如果課堂教學時間允許,教師還可以安排學生自主列舉一些不等式,畫出相應函數的圖象,數形結合地演示不等式的解集.
教學環節4:課堂小結,布置作業
小結問題1:本課學習了從一次函數視角看一元一次方程,可舉例說說你是如何理解的嗎?
小結問題2:從函數圖象的角度分析一元一次不等式x-3>1的解集.
小結問題3:從函數圖象的角度分析方程x-3=1-x的解,以及不等式x-3>1-x的解集.
設計意圖 “小結問題1”主要是從知識層面組織學生進行回顧,學生可以通過舉例說出自己的理解;隨后兩個小結問題則明確要求學生結合具體的例子數形結合地分析、理解,以反饋學生對本課所學內容的掌握情況. 也就是說,小結問題的設計針對具體課型應有所區別. 比如有些新授課知識點多、概念也多,此時可以側重于知識、概念的回顧與梳理,而像本課這樣突出數形結合眼光、分析策略的,重在實際操作與解題運用,此時小結問題可以相機地運用具體習題來反饋學情.
教學立意的進一步闡釋
1. 遵循教材順序,基于舊知引出新知
教材編寫組都是由數學家、數學教育家、數學教研專家、數學專家教師等組成的,對于教材內容的編排順序是反復考量、精心設計的. 一般情況下,一線教師在沒有深刻理解的情況下,不宜本著所謂“學材重組”的理念變動教材順序,而應盡量遵循教材順序,想清教學出發點、學情生長點,基于舊知引出新知.
2. 預設對話追問,引導學生概括新知
教師在備課時,除了要研究教材、精心選題而外,還要重視各個教學環節中問題的呈現方式. 筆者以為,教師首先要加強對話追問的過渡語的預設. 比如,不必急于呈現一個問題的全貌(有些習題單式導學案常有類似現象),可以使用PPT出示一個問題的題干,讓學生理解、讀懂題干之后,再安排學生想想能提出怎樣的問題. 如果學生能想出貼近本課的問題,教師可順勢引出本課要研究的問題,這樣的對話追問就起到了很好的問題過渡作用. 另外,教師要重視啟發式教學,要引導學生概括新知. 比如,對于一次函數與一元一次方程之間的關系,教師要讓學生從圖象中觀察一次函數圖象與x軸交點橫坐標與相應的一元一次方程的根之間的對應關系,然后讓學生變式舉例,從不同的角度發現規律,進一步引導學生歸納、概括規律,最后走向一般,概括本課所學的新知. 如果學生概括的語句不夠完整或有缺陷,教師可組織活動進一步完善或修正,體現新知生成的“曲折”——數學概念的生成常常有“由粗糙到精致”的過程.
3. 重視數形結合,促進學生感悟方法
從函數觀點看方程、不等式的教學關鍵就是訓練學生利用數形結合解題的能力. 史寧中教授在一些報告中反復說過“數學是‘看’出來的”,大概也包含這樣的思想. 以本文關注的課例來說,教師要重視學生利用數形結合思想分析問題的能力的培養. 比如,在復習舊知環節,讓學生對照兩個一次函數圖象的交點,說出對應的二元一次方程組的解;在引出新知環節,讓學生指著圖象,辨別一次函數圖象(直線)與x軸公共點的橫坐標,并指出對應的一元一次方程的解;在變式拓展環節,讓學生畫圖分析一次函數的函數值的取值范圍與對應的一次不等式的解集之間的關系.

