選編“形異質(zhì)同”題

作者簡(jiǎn)介：李井凡（1979—），本科學(xué)歷，中學(xué)一級(jí)教師，從事中學(xué)數(shù)學(xué)教育教學(xué)工作.

[摘 要] 傳統(tǒng)的幾何專題課有開(kāi)放式專題課、數(shù)學(xué)思想方法的專題課、閱讀理解專題課等，近年來(lái)以“一圖一課”“微專題課”等為代表的專題教學(xué)漸漸得到很多教師的實(shí)踐與研究. 這類課型主題聚焦，求深、求透，能有效提升解題教學(xué)效率.

[關(guān)鍵詞] “形異質(zhì)同”;幾何專題課;一圖一課;回顧反思

近年來(lái)幾何專題課得到不少教師的關(guān)注和研究，這類專題課常常聚焦某一個(gè)基本圖形或某一類設(shè)問(wèn)方式，切口較小，有教師將其描述為“微專題課”“一圖一課”等. 下面是筆者整理的最近在備課組內(nèi)開(kāi)設(shè)的一節(jié)“探究?jī)蓷l線段之間的數(shù)量關(guān)系”專題研討課的教學(xué)流程，并跟進(jìn)了一些教學(xué)思考，供大家研討.

“探究?jī)蓷l線段之間的數(shù)量

關(guān)系”專題課教學(xué)流程

教學(xué)環(huán)節(jié)1：從經(jīng)典問(wèn)題出發(fā)

問(wèn)題1：如圖1所示，四邊形ABCD是正方形，連接對(duì)角線BD，作∠CBD的平分線交CD于點(diǎn)E.

（1）求證：DE=CE.

（2）過(guò)點(diǎn)D作DH⊥BE，交BC的延長(zhǎng)線于點(diǎn)G，垂足為H.

①求證：H是DG的中點(diǎn);

②若BH上有一點(diǎn)P，滿足PB=PD，探究PD與BE之間的數(shù)量關(guān)系，并說(shuō)明理由.

<D：＼數(shù)學(xué)教學(xué)通訊中旬＼2023數(shù)學(xué)教學(xué)通訊中旬（12期）＼2023數(shù)學(xué)教學(xué)通訊中旬（12期） c＼12-165.tif>[圖1][B][D][C][E][A]

解法預(yù)設(shè)與教學(xué)組織：教師出示正方形ABCD之后，不要急于出示小問(wèn)，可以先讓學(xué)生回顧基礎(chǔ)問(wèn)題“若正方形ABCD的邊長(zhǎng)為1，求其對(duì)角線BD的長(zhǎng)”，然后依次研究第（1）（2）問(wèn). 對(duì)于第（1）問(wèn)，學(xué)生可以有不同的解法，比如面積法、角平分線的性質(zhì)等，教師可以通過(guò)追問(wèn)讓學(xué)生分享他們的不同思路. 對(duì)于第（2）①問(wèn)，需要學(xué)生補(bǔ)全圖形后，證明△BDH≌△BGH，從而得H是DG的中點(diǎn);對(duì)于第（2）②問(wèn)，當(dāng)點(diǎn)P滿足PB=PD時(shí)，可知△PDH是等腰直角三角形，從而得PD=DH，結(jié)合△BCE≌△DCG，可得BE=DG=2DH，于是BE=PD.

教學(xué)環(huán)節(jié)2：以正方形為背景的題組

問(wèn)題2：如圖2所示，正方形ABCD的對(duì)角線BD所在直線可以看成正方形ABCD的一條對(duì)稱軸.

（1）畫出正方形ABCD的所有對(duì)稱軸.

（2）如圖3所示，以點(diǎn)B為圓心、BC的長(zhǎng)為半徑的圓弧交其中一條對(duì)稱軸于點(diǎn)E，連接OE，DE.

①求∠DCE的度數(shù);

②分析OE與DE之間的數(shù)量關(guān)系.

解法預(yù)設(shè)與教學(xué)組織：第（1）問(wèn)比較基礎(chǔ)，讓學(xué)生從軸對(duì)稱的角度思考正方形問(wèn)題，這為第（2）①問(wèn)構(gòu)造并發(fā)現(xiàn)等邊三角形BCE做鋪墊，于是可得∠DCE=30°. 解決第（2）②問(wèn)的關(guān)鍵是將解題目光聚焦在△DEO中，分析出該三角形有兩個(gè)特殊的銳角30°，45°，從而想到過(guò)點(diǎn)E作EH⊥DO，垂足為H，得到DE=OE.

教學(xué)環(huán)節(jié)3：以等腰直角三角形為背景的綜合題

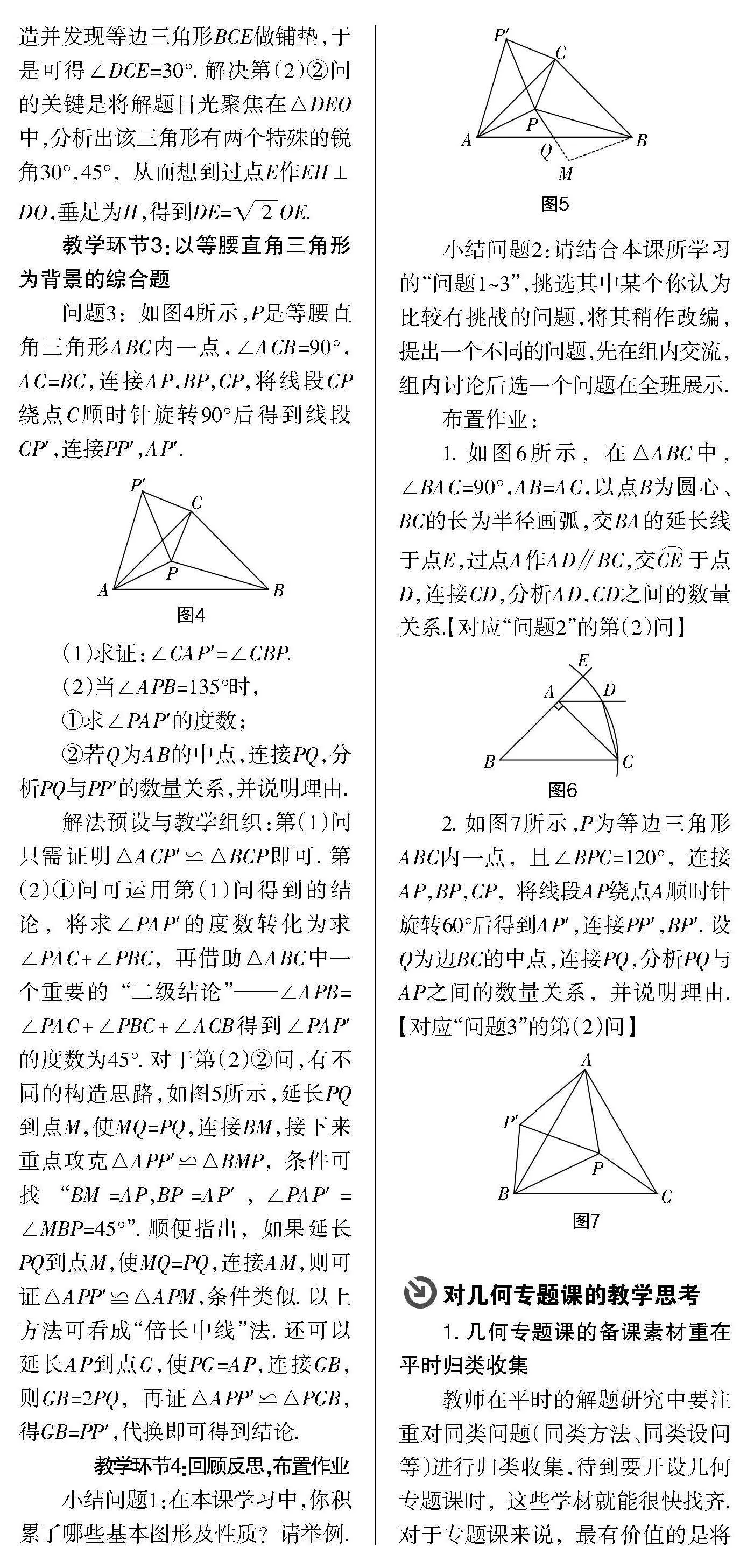
問(wèn)題3：如圖4所示，P是等腰直角三角形ABC內(nèi)一點(diǎn)，∠ACB=90°，AC=BC，連接AP，BP，CP，將線段CP繞點(diǎn)C順時(shí)針旋轉(zhuǎn)90°后得到線段CP′，連接PP′，AP′.

（1）求證：∠CAP′=∠CBP.

（2）當(dāng)∠APB=135°時(shí)，

①求∠PAP′的度數(shù);

②若Q為AB的中點(diǎn)，連接PQ，分析PQ與PP′的數(shù)量關(guān)系，并說(shuō)明理由.

解法預(yù)設(shè)與教學(xué)組織：第（1）問(wèn)只需證明△ACP′≌△BCP即可. 第（2）①問(wèn)可運(yùn)用第（1）問(wèn)得到的結(jié)論，將求∠PAP′的度數(shù)轉(zhuǎn)化為求∠PAC+∠PBC，再借助△ABC中一個(gè)重要的“二級(jí)結(jié)論”——∠APB=∠PAC+∠PBC+∠ACB得到∠PAP′的度數(shù)為45°. 對(duì)于第（2）②問(wèn)，有不同的構(gòu)造思路，如圖5所示，延長(zhǎng)PQ到點(diǎn)M，使MQ=PQ，連接BM，接下來(lái)重點(diǎn)攻克△APP′≌△BMP，條件可找“BM=AP，BP=AP′，∠PAP′=∠MBP=45°”. 順便指出，如果延長(zhǎng)PQ到點(diǎn)M，使MQ=PQ，連接AM，則可證△APP′≌△APM，條件類似. 以上方法可看成“倍長(zhǎng)中線”法. 還可以延長(zhǎng)AP到點(diǎn)G，使PG=AP，連接GB，則GB=2PQ，再證△APP′≌△PGB，得GB=PP′，代換即可得到結(jié)論.

教學(xué)環(huán)節(jié)4：回顧反思，布置作業(yè)

小結(jié)問(wèn)題1：在本課學(xué)習(xí)中，你積累了哪些基本圖形及性質(zhì)？請(qǐng)舉例.

小結(jié)問(wèn)題2：請(qǐng)結(jié)合本課所學(xué)習(xí)的“問(wèn)題1～3”，挑選其中某個(gè)你認(rèn)為比較有挑戰(zhàn)的問(wèn)題，將其稍作改編，提出一個(gè)不同的問(wèn)題，先在組內(nèi)交流，組內(nèi)討論后選一個(gè)問(wèn)題在全班展示.

布置作業(yè)：

1. 如圖6所示，在△ABC中，∠BAC=90°，AB=AC，以點(diǎn)B為圓心、BC的長(zhǎng)為半徑畫弧，交BA的延長(zhǎng)線于點(diǎn)E，過(guò)點(diǎn)A作AD∥BC，交于點(diǎn)D，連接CD，分析AD，CD之間的數(shù)量關(guān)系.【對(duì)應(yīng)“問(wèn)題2”的第（2）問(wèn)】

2. 如圖7所示，P為等邊三角形ABC內(nèi)一點(diǎn)，且∠BPC=120°，連接AP，BP，CP，將線段AP繞點(diǎn)A順時(shí)針旋轉(zhuǎn)60°后得到AP′，連接PP′，BP′. 設(shè)Q為邊BC的中點(diǎn)，連接PQ，分析PQ與AP之間的數(shù)量關(guān)系，并說(shuō)明理由.【對(duì)應(yīng)“問(wèn)題3”的第（2）問(wèn)】

對(duì)幾何專題課的教學(xué)思考

1. 幾何專題課的備課素材重在平時(shí)歸類收集

教師在平時(shí)的解題研究中要注重對(duì)同類問(wèn)題（同類方法、同類設(shè)問(wèn)等）進(jìn)行歸類收集，待到要開(kāi)設(shè)幾何專題課時(shí)，這些學(xué)材就能很快找齊. 對(duì)于專題課來(lái)說(shuō)，最有價(jià)值的是將一些“形異質(zhì)同”問(wèn)題關(guān)聯(lián)在一起開(kāi)展教學(xué)，這樣能提高學(xué)生的解題能力，能促進(jìn)學(xué)生識(shí)別具有相同或相近深層結(jié)構(gòu)問(wèn)題的能力.

2. 幾何專題課的教學(xué)流程應(yīng)該由易到難展開(kāi)

開(kāi)展幾何專題課教學(xué)時(shí)，教師宜先從學(xué)生熟悉的經(jīng)典問(wèn)題出發(fā)，讓更多的學(xué)生在開(kāi)課階段便能理解、參與，然后進(jìn)行一些變式、提升與拓展，把學(xué)生的思維卷入有挑戰(zhàn)的課堂問(wèn)題中. 教師在課前預(yù)設(shè)的一些鋪墊問(wèn)題有時(shí)可以“密集”一些，但是在實(shí)際教學(xué)時(shí)要根據(jù)學(xué)生的學(xué)情相機(jī)呈現(xiàn)，比如學(xué)生的學(xué)情較好時(shí)，有些鋪墊問(wèn)題就不急于給出，而是要讓學(xué)生獨(dú)立面對(duì)挑戰(zhàn)，如果有少數(shù)優(yōu)秀學(xué)生能貫通思路，則教師可以通過(guò)追問(wèn)暴露其思維過(guò)程，讓那些理解稍慢的學(xué)生也能跟上班級(jí)節(jié)奏. 這里可提及印發(fā)給學(xué)生的“學(xué)案”的設(shè)計(jì)技巧. 一般來(lái)說(shuō)，像上文課例中的“問(wèn)題”的“題干”和“基礎(chǔ)圖形”均可以印制在“學(xué)案”上，但是后續(xù)設(shè)問(wèn)一般不“和盤托出”，而是借助課件漸次呈現(xiàn)或相機(jī)出示，這樣的學(xué)案就是所謂的“留白式學(xué)案”.

3. 幾何專題課的小結(jié)與作業(yè)布置要精心預(yù)設(shè)

曹才翰、章建躍兩位先生在《中學(xué)數(shù)學(xué)教學(xué)概論（第二版）》一書中關(guān)于解題教學(xué)曾指出：“在解題過(guò)程中，關(guān)鍵是能靈活地將問(wèn)題轉(zhuǎn)化為自己熟悉的表述方式，而轉(zhuǎn)化的過(guò)程就是尋找問(wèn)題的條件、結(jié)論的等值語(yǔ)言表示，連接相關(guān)通道的過(guò)程. 因此，加強(qiáng)‘多元聯(lián)系表示’思想的運(yùn)用是提高解題能力的基本途徑”. 從上文課例中可以看出，幾何專題課同樣需要教師精心預(yù)設(shè)課堂小結(jié). 上文課例運(yùn)用兩個(gè)小結(jié)問(wèn)題，促進(jìn)學(xué)生全面回顧、反思本課所學(xué)，特別是“小結(jié)問(wèn)題2”，更是讓學(xué)生參與問(wèn)題的設(shè)計(jì)與改編. 想來(lái)，這也是在積極實(shí)踐“多元聯(lián)系表示”思想吧！