基于解題經驗培養的數學教學研究

作者簡介：沈習輝（1977—），本科學歷，中學高級教師，從事初中數學教學與研究工作，宿遷市數學骨干教師，宿城區數學學科帶頭人.

[摘 要] 建構主義理論認為問題的解決需以原有的解題經驗為基礎，在新舊問題之間建立聯系是提升解題經驗的法寶. 本文以“梯形”的解題教學為例，認為有效追問能幫助學生進一步理清解題思路，形成解題經驗;引導學生經歷嘗試，可讓學生在自主探索中驗證經驗的可靠性;及時總結提煉，可提升學生的解題經驗，為形成觸類旁通的解題能力奠定基礎.

[關鍵詞] 經驗;追問;概括

實際教學中，有些教師將問題的正確答案作為教學的終點，教學過程因缺乏追問、拓展與總結，導致學生無法形成良好的解題經驗，難以達到舉一反三的解題能力. 為了改變這一現狀，筆者對如何幫助學生形成良好的解題經驗進行了大量的研究，發現解題教學從追問、嘗試與總結三個方面出發，能起到較好的成效.

借助追問，形成經驗

學貴有疑，追問屬于創疑的一種方式. 適時追問可引發學生思考已經回答過的問題，讓學生進一步理清解題思路與方法，為形成解題經驗奠定基礎. 但不少教師僅將目光鎖定在原式問題的設計與處理上，忽略對問題的拓展與延伸，課堂常因缺乏追問導致無法達到深度學習的階層. 這部分教師在學生回答問題后，直接給予肯定或否定，而不進行具體的評價，導致學生無法在自身原有的基礎上得到更深層次的理解.

獲得結論并不是最重要的，重要的是獲得結論的過程. 追問對促進學生解題經驗的積累具有重要意義，不論學生的回答是正確還是錯誤，作為一名合格的教師都應讓學生闡述自己的想法，讓學生通過對結論形成的追憶暴露真實的思維過程，以覺察思維方法的正確性.

事實證明，一個充滿智慧的教師不僅能設計出精巧的問題，還能根據學生的答題情況與思路歷程提出恰當的追問，達到促進經驗形成的作用.

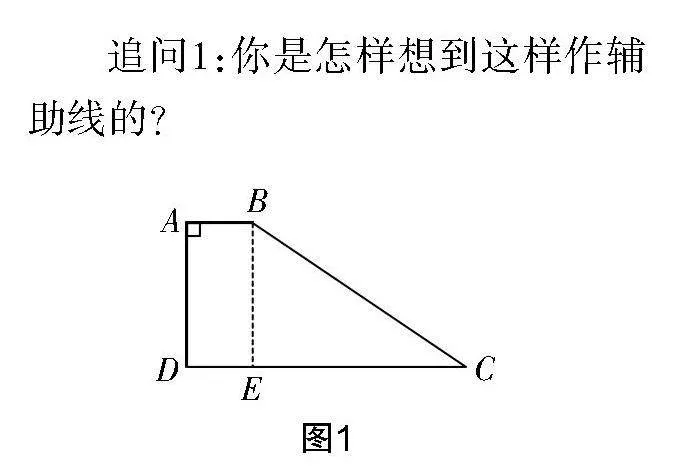
例1 如圖1所示，在直角梯形ABCD中，AB∥DC，DA⊥AB，AB=1，CD=4，AD=2，求BC的長.

經思考，學生呈現出如下解題過程：過點B作AD的平行線與線段CD相交于點E，此時BE與DC垂直，由此可確定四邊形ADEB為一個矩形，根據矩形性質可知BE=2，CE=3，根據勾股定理可得BC=.

追問1：你是怎樣想到這樣作輔助線的？

設計意圖 這個追問的目的在于讓學生說一說輔助線得來的依據，在這個問題的引領下，學生總結出：在直角梯形中構造出矩形，可以獲得許多相等的量，將多個條件集中到一起，可以構造出待求線段相關的直角三角形，有了直角三角形就能結合勾股定理獲得線段的值.

追問2： 作出的輔助線和梯形中原有的線段存在聯系嗎？

設計意圖 此問的目的在于引導學生從多個維度來思考輔助線的作法，所作輔助線可從梯形的高出發，也可從AD的平行線或平移AD的角度來思考. 多視角思考與分析輔助線，不僅豐富了學生的學習經驗，還為解題方法的析離奠定基礎.

方法總結：追問的應用，讓學生發現作輔助線是解決此類問題的關鍵切入口，輔助線的目的在于集中分散的三邊，至于從什么視角（高、平行或平移）來作輔助線，可根據實際情況來決定. 在追問下，學生獲得解決這一類問題的經驗——擇取恰當的點與方法作輔助線.

歷經嘗試，驗證經驗

當學生獲得一定的解題經驗后，往往會有種躍躍欲試的興奮感，教師可趁熱打鐵，結合學情與教情設置難度與梯度恰當的問題，讓學生嘗試自主應用這些經驗，以更進一步強化與鞏固學習經驗，增強學習信心，提升學習能力. 值得注意的是學生在原有認知經驗和新問題之間必須有跨度，又有一定的聯系，切忌出現一步到位的問題，要讓學生擁有經驗遷移的機會.

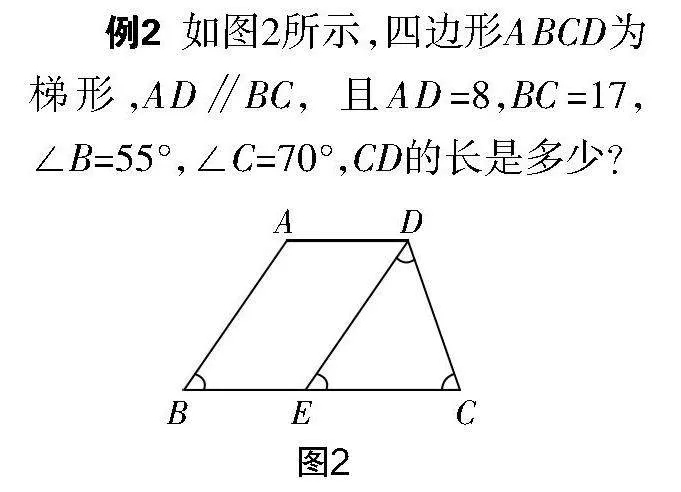
例2 如圖2所示，四邊形ABCD為梯形，AD∥BC，且AD=8，BC=17，∠B=55°，∠C=70°，CD的長是多少？

學生提出如下解題方法：過點D作DE與AB平行與BC邊相交于點E. 根據DE∥AB的條件可知AD=BE，∠CED=55°. 根據∠C=70°的條件，可知∠CDE=55°，由此可推導出EC=DC. 因為AD=8，BC=17，可確定DC=9.

本題與例1有一定關聯，解題的關鍵也是作輔助線，但本題通過矩形的構造解決問題顯然不行，但從本題所給定角的度數出發，易聯想到作平行線構造角的方法，過點D作DE與AB平行與BC邊相交于點E后就構造出一個平行四邊形，那么AD=BE則自然生成;從∠C=70°的條件，易聯想到∠CDE=55°，問題隨之解決.

從本題作輔助線的方法來看，除了構造出平行四邊形之外，還與例1相似，將盡量多的條件集中到了一個三角形里面. 借助已有的教學經驗，在解決完本題后，同樣要求學生說說解決問題的切入點與所作輔助線和梯形原有線段之間的關系. 學生在表述的過程中發散思維，認為既可以理解為作AB邊的平行線，也可以理解為平移AB邊獲得結論.

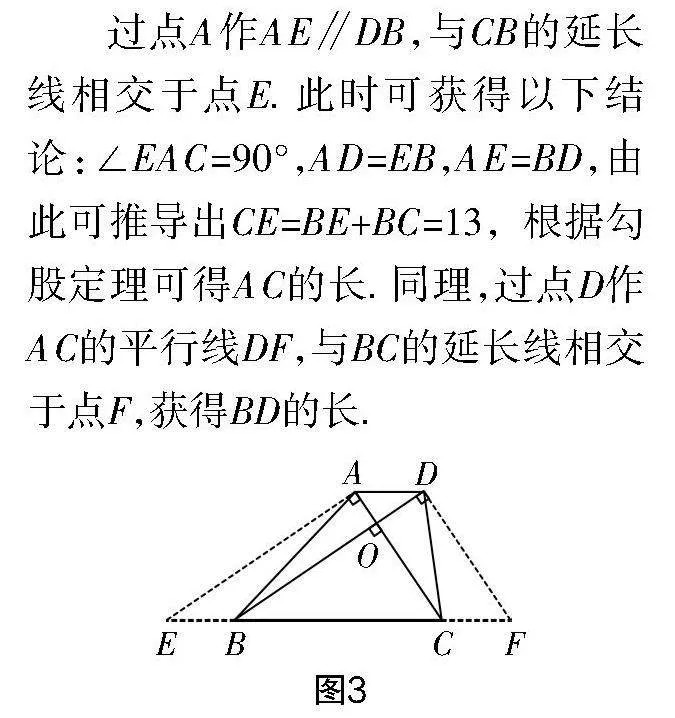
例3 如圖3所示，已知梯形ABCD中的AD平行于BC，AC與BD垂直于點O，AD，BD，BC的長度分別為3，12，10，求AC的長度.

過點A作AE∥DB，與CB的延長線相交于點E. 此時可獲得以下結論：∠EAC=90°，AD=EB，AE=BD，由此可推導出CE=BE+BC=13，根據勾股定理可得AC的長. 同理，過點D作AC的平行線DF，與BC的延長線相交于點F，獲得BD的長.

本題與前兩題相比發生了一些變化，前兩題的輔助線都位于梯形內部，而本題的輔助線卻處于梯形外部，這與學生已有的認知經驗形成矛盾. 認知沖突的形成為進一步發展思維奠定了基礎，此處需引導學生分析“本題與前兩題相比，哪里不一樣？解題關鍵是什么？有什么收獲等”.

學生將初步形成的認知經驗應用到實際問題中，不僅進一步夯實了知識基礎，還獲得了解題技巧，驗證了經驗的可靠性.

總結提煉，提升經驗

解決梯形相關問題的關鍵在于作輔助線，學生一旦經歷且積累了豐富的經驗，形成獨特的解題技巧后，教師可帶領學生對經驗進行概括性總結，幫助學生形成觸類旁通的解題能力. 鑒于這些經驗是零散、無條理的，教師可帶領學生將這些零散的經驗進行概括與提煉，形成有序思維.

提煉過程如下：①帶領學生思考每一種情況下所作輔助線的共同點，將輔助線與原有線段建立關聯;②從平移的視角來觀察梯形固有線段，分析其平移后的狀況;③觀察隱含的線段，如梯形的對角線、高、角平分線等是否可以平移，平移之后會發生什么情況？④思考梯形中的線段除了可以進行平移處理之外，能否延長、縮短等;⑤思考線段之外條件的變化，如角的變大或縮小等;⑥熔煉上述思考;⑦甄別已經遇到的問題，探索輔助線的幾類作法，為后續解題建立路徑次序;⑧遇到復雜的梯形類問題，主動應用如上策略進行驗證，豐富自身的解題經驗;⑨靈活應用所獲得的解題經驗，形成解題能力.

以上步驟的實施需結合具體問題而定，并非要求完全按部就班地應用在解決某一類問題中，可根據學生的實際認知經驗進行循序漸進的逐步滲透，讓學生通過對一類問題的研究，總結提煉解題路徑與方法，再將這些方法遷移到另一類問題的解決中去，形成良好的循環.

從本節課梯形問題的研究來看，解決幾何問題需依托對基本元素的變換，如線段的平移旋轉或角度的變化等，再結合嚴謹的推理形成結論. 結合已知條件與待求結論，通過對線或角等基本元素的變化就能突破一些解題障礙，尤其是恰當的輔助線是解決復雜幾何問題的重中之重.

總之，想要從真正意義上突破“遇到做過的題目就會，遇到沒做過的題目就懵”的狀態，就需從解題經驗的培養著手，讓學生在經驗的形成、驗證與提升中獲得舉一反三的能力.