利于新能源消納的大工業用戶電價策略研究

曹 暉

國網湖北省電力公司鄂州供電公司營銷部, 湖北 鄂州 436000

0 引言

隨著新能源的快速發展和廣泛應用,其消納問題日益突出。在此背景下,大工業用戶作為電力消費的主要力量,其電力需求特點和電價策略對于促進新能源消納具有重要意義[1]。本文旨在對利于新能源消納的大工業用戶電價策略進行分析,并探討如何通過合理的調峰負荷模型和時段劃分來優化新能源消納,通過研究期望能為促進新能源消納、提高大工業用戶能源利用效率以及推動可持續能源發展作出貢獻。

1 大工業用戶調峰負荷模型與時段劃分

1.1 大工業用戶負荷轉移模型

在大工業用戶電力需求波動較大的情況下,負荷轉移模型可用來描述如何在電力供應充足時將部分負荷轉移到低負荷時段,以實現負荷平衡和優化能源利用[2]。

以下是一個常用的大工業用戶負荷轉移模型的示例。假設大工業用戶的負荷轉移模型可表示為線性關系。

L(t)=a×P(t)+b×G(t)+c

(1)

式中:L(t)為時刻t的總負荷量;P(t)為用戶的基準負荷;G(t)為負荷轉移量;a、b和c為系數。

負荷轉移量G(t)可根據負荷轉移策略和供需情況來確定。常見的負荷轉移策略包括根據電力系統的負荷曲線、市場電價或用戶需求來調整用電行為,用戶可將部分負荷從高峰時段轉移到低負荷時段,以降低對系統峰值負荷的貢獻。

負荷轉移模型中的系數a、b和c可根據實際情況進行估計或優化。它們的取值可反映用戶的基準負荷、負荷轉移的影響程度以及用戶在無負荷轉移時的固定負荷。

1.2 峰谷平時段劃分策略

根據上述大工業用戶負荷轉移模型,可利用該模型來輔助進行峰谷平時段的劃分策略。基于大工業用戶負荷轉移模型來實施峰谷平時段劃分策略,以引導用戶在合適的時段進行用電,實現負荷平衡和優化新能源消納。該策略將有助于提高能源利用效率,減少系統負荷峰值,并促進新能源的可持續發展[3]。

1)數據收集與預處理。收集歷史負荷數據和新能源出力數據,并進行預處理,包括去除異常值、平滑處理等,以獲得可靠的數據基礎。

2)負荷轉移模型參數估計。利用負荷轉移模型,通過歷史負荷數據和相關參數估計方法,例如最小二乘法、最大似然估計等,來確定模型中的系數a、b和c。

3)負荷轉移量計算。根據負荷轉移模型中的系數和歷史負荷數據,計算各時刻的負荷轉移量G(t)。

4)峰谷平時段劃分。基于負荷轉移量G(t)和新能源出力情況,采用閾值法、權重法、時段劃分等方法來確定峰谷平時段。

2 促進新能源消納的大工業用戶電價策略

2.1 峰谷分時電價促進新能源消納機制分析

根據電力系統的負荷情況和新能源出力情況,將一天劃分為多個時段,例如峰時段、谷時段和平時段。在峰時段,由于負荷較高或新能源出力較低,設定較高的電價,以鼓勵大工業用戶在此時段減少用電或通過負荷轉移將部分負荷轉移到低谷時段;在谷時段,由于負荷較低或新能源出力較高,設定較低的電價,以吸引大工業用戶增加用電或增加新能源消納;平時段則設置適中的電價[4]。

2.2 促進新能源消納的機組調度策略

為有效消納新能源,大工業用戶可采取機組調度策略。機組調度是指根據新能源出力情況和負荷需求,合理安排不同類型的發電機組運行模式和出力調節,以滿足大工業用戶的用電需求和新能源的消納要求。通過合理的機組調度策略,大工業用戶可靈活調整用電行為,以適應新能源的波動性,并最大程度地促進新能源的消納和利用。

2.3 促進新能源消納的峰谷平時段優化模型

為進一步優化新能源消納和大工業用戶的用電行為,可建立峰谷平時段優化模型。該模型考慮了大工業用戶的電費滿意度、目標函數和約束條件,并采用粒子群算法進行求解[5]。

2.3.1 用戶電費滿意度

用戶電費滿意度是衡量大工業用戶對電費支出滿意程度的指標。可根據用戶對不同時段的電價敏感度,結合實際情況,設定不同時段的電費滿意度權重。例如在低谷時段,用戶對電費支出較為敏感,可賦予較高的滿意度權重;而在峰時段,用戶對電費支出較為不敏感,可賦予較低的滿意度權重。用戶滿意度調查結果見表1。

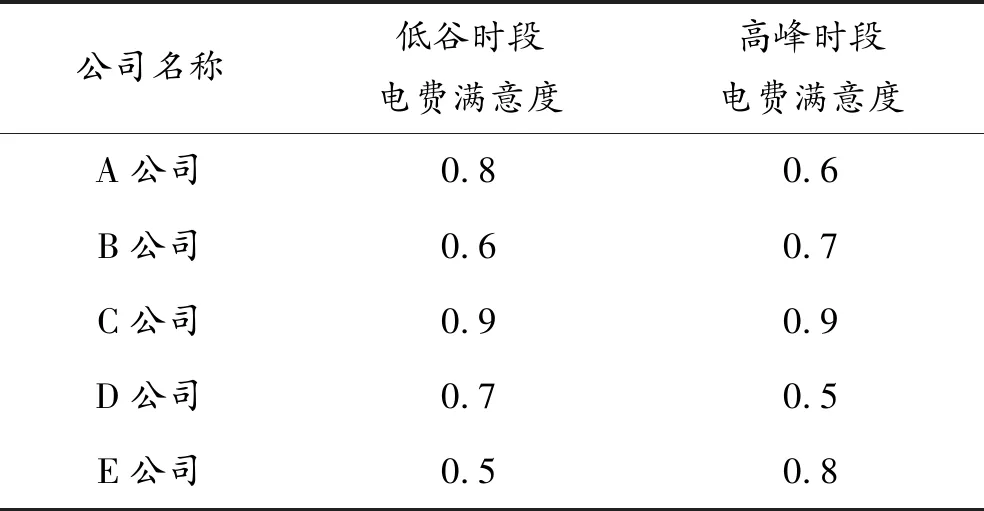
表1 用戶電費滿意度調查結果

2.3.2 目標函數及約束條件

目標函數:目標是最小化大工業用戶的總電費支出,并在此過程中促進新能源消納。

目標函數:minimizeF(t)

式中:F(t)表示時段t的電費支出。

約束條件:

1)總用電量約束:大工業用戶的總用電量應滿足預設的需求范圍。

G(t)≤D(t),?t

式中:G(t)為時段t的實際用電量;D(t)為時段t的需求量。

2)新能源消納約束:可設置一個新能源消納比例的約束條件,確保在每個時段中消納一定比例的新能源。

(G(t))-Gren(t)) ≥β×D(t),?t

式中:Gren(t)為時段t的可再生能源發電量;β表示設定的新能源消納比例。

計算過程:

1)對于每個時段t,計算F(t)的值,表示時段t的電費支出,可以基于電價策略和用電量計算得出。

2)根據總用電量約束,計算實際用電量G(t)與需求量D(t)的差異。

3)根據新能源消納約束,計算實際用電量與可再生能源發電量之間的差異,并與需求量的比例進行比較。

2.3.3 粒子群算法求解

上節將使用粒子群算法來求解促進新能源消納的峰谷平時段優化模型。以下是關于粒子群算法的求解過程的說明。

1)初始化:設置粒子群的大小(例如N個粒子)和迭代次數(例如T次迭代);隨機初始化每個粒子的位置和速度;為每個粒子設置初始最優位置(Pbest)和全局最優位置(Gbest)。

2)迭代過程如下。①更新粒子的速度和位置:通過考慮當前速度、個體最優位置和全局最優位置,更新粒子的速度和位置。②計算適應度函數:根據粒子的位置計算目標函數的值,即電費支出F(t)。③更新個體最優位置和全局最優位置:如果當前粒子的適應度優于個體最優位置,則更新個體最優位置;如果當前粒子的適應度優于全局最優位置,則更新全局最優位置。④結束迭代條件:達到設定的最大迭代次數或達到滿意的優化結果。

3)輸出結果:輸出全局最優位置對應的電費支出F(t)作為最終的優化結果;分析最優位置對應的用電量分配和時段優化結果。

通過粒子群算法的迭代過程,可搜索到最優解,即能夠在滿足約束條件的情況下最小化電費支出。最終的優化結果將提供關于用電量分配和時段優化的信息,以促進新能源消納的目標。

2.3.4 峰谷平時段優化仿真流程

峰谷平時段優化仿真流程的基本流程圖如圖1所示。開始時,初始化參數和變量,并生成初始粒子群;然后,計算每個粒子的適應度函數,更新個體最優位置和全局最優位置;接下來,判斷終止條件,如果不滿足條件,則繼續更新粒子的速度和位置,并再次計算適應度函數和更新最優位置,直到滿足終止條件為止;最后,仿真結束。

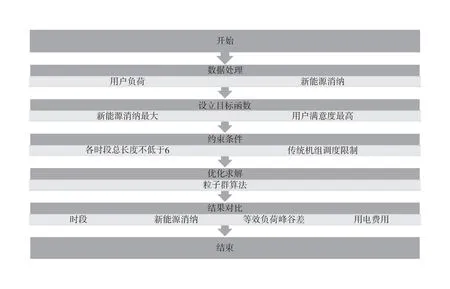
圖1 仿真流程圖

2.3.5 時段優化結果分析

示例中,比較了調整前和調整后的用電量以及相應的電費支出。可觀察到,調整后的用電量在峰時段1和峰時段2有所減少,而在平時段和谷時段有所增加。這表明峰谷平時段優化策略對用電行為進行了調整,以更好地適應新能源消納需求。通過表2可直觀地比較調整前和調整后的用電量和電費支出數據。這個對比可幫助評估峰谷平時段優化策略的效果,并確定其對電費支出的影響。同時,可進一步分析其他因素,例如用戶滿意度和供需平衡,以全面評估優化策略的綜合效果。

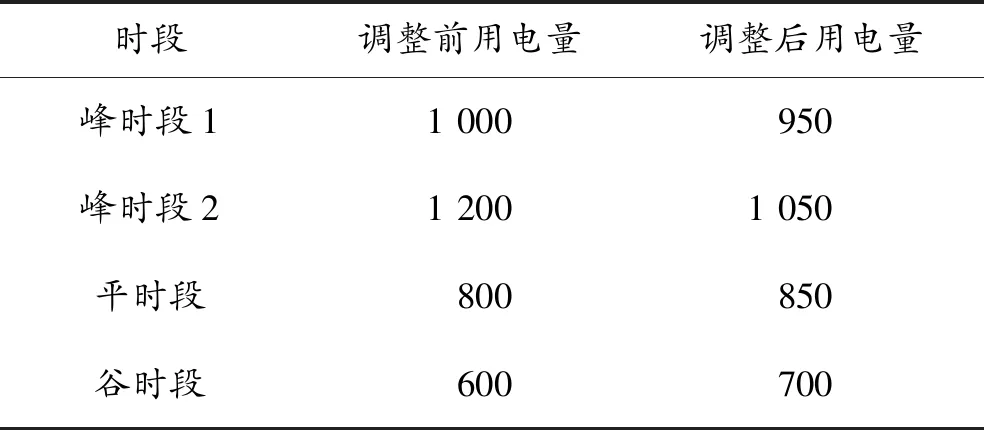
表2 峰谷平時段優化調整前和調整后的數據對比 單位:k·Wh

3 結束語

利于新能源消納的大工業用戶電價策略研究對于實現能源可持續發展具有重要意義。通過合理制定電價策略、優化時段分配和采用適當的優化算法,可有效促進新能源的消納,降低能源消耗和環境影響,實現可持續發展目標。在新能源與環境保護的背景下,通過優化電價策略和時段分配,可更好地推動新能源的發展與利用,為能源結構轉型和可持續發展作出貢獻。