具有自適應權矩陣的空間滯后模型:權矩陣構造及模型估計
梅長林, 王 琪, 續秋霞
(西安工程大學理學院,西安 710048)
0 引言
空間滯后模型[1]或稱之為空間自回歸模型是空間數據分析的一種重要模型。該模型在一般線性回歸模型中引入了因變量的空間滯后項,同時考慮自變量的線性效應和因變量的空間自相關性,在空間計量經濟學、環境科學、流行病學等眾多領域得到廣泛的應用。

對于上述空間滯后模型,已發展了諸如最大似然估計[1]、兩階段最小二乘估計[2]、廣義矩估計[3]等多種估計方法,并建立了有關估計量的大樣本性質[3–4]。雖然空間滯后模型及其他空間計量經濟模型在應用上獲得了巨大成功[5],但實際困難之一是其中空間權矩陣的確定問題,不同的空間權矩陣可能會嚴重影響最終的分析結果[6–7]。為此,作為空間數據自相關性分析的一個重要內容,人們在長期的研究中發展了各種空間權矩陣的構造方法:基于Tobler 地理學第一定律[8](即距離越近的事物間的相關性越大)提出的如0-1 值空間權矩陣、逆距離權矩陣、距離衰減權矩陣等多種形式,高樂[9]對這些經典的空間權矩陣的構造方法進行了總結;基于空間局部統計量[10]的空間權矩陣構造方法,如Getis 和Aldstadt[11]的基于臨界距離和Aldstadt 和Getis[12]的AMOEBA 空間權矩陣的確定方法。但以上方法均是在模型擬合之前就需要確定其中的空間權矩陣,未能充分考慮因變量觀測數據自身所蘊含的自相關性信息,因而有一定的主觀性。尤其是最常用的0-1 值空間權矩陣,由模型(1)可知,任何給定空間目標單元處因變量的觀測值與其鄰接單元處的觀測值的相關性都相同(即ρ的常數倍),這未能充分體現Tobler 定律中相關性應隨距離衰減的規律。近期,基于機器學習技術確定空間權矩陣的方法得到發展。例如,Seya 等[13]將可逆跳馬爾科夫鏈蒙特卡羅技術與模擬退火方法相結合,建立了自動確定空間權矩陣的算法;Kostov[14]提出了基于逐分量模型,提升算法在一類事先給定的空間權矩陣類中選擇最優的權矩陣;任英華和游萬海[15]將該方法應用于空間滯后模型,對我國城市服務業集聚機理進行了實證分析;Lam 和Souza[16]通過引入稀疏調節矩陣,基于自適應LASSO 算法選擇空間權矩陣。雖然這些數據驅動的空間權矩陣選擇方法具有很好的自適應性,但通常都面臨較高的計算代價以及權矩陣的可解釋性問題。同時,和經典的權矩陣選擇方法一樣,對于空間滯后模型(1)來說,因變量在任一目標單元處的觀測值與其鄰接單元處的觀測值之間的相關性強度只是一個按固定比例ρ的一個壓縮,即是權矩陣中元素的線性函數。
本文以事先給定的描述n個地理單元空間鄰接結構的0-1 值權矩陣為基礎,將其中具有空間鄰接關系的元素(即元素“1”)替換為所對應的兩個空間單元之間距離的單調減函數,同時將模型(1)中的自回歸參數ρ按一定方式嵌入到距離函數中,變為控制函數下降速度的參數,該參數如模型(1)中的自回歸參數ρ一樣,可以結合模型的估計方法予以估計。本文在空間權矩陣元素的設計上,通過引入控制其隨距離下降速度的參數,使空間權矩陣更具靈活性,在一定程度上克服了經典方法中確定空間權矩陣的主觀性;將空間權矩陣中的控制參數的選擇與模型估計方法結合,基于數據驅動方法自適應地確定該參數,可使所確定的空間權矩陣能更有效地反映客觀實際;較之于機器學習技術確定空間權矩陣的方法,所確定的空間權矩陣各元素不僅能體現Tobler 地理學第一定律的主旨,而且有很好的可解釋性;基于本文提出的空間權矩陣所建立的新的空間滯后模型仍可以像傳統模型(1)一樣,利用最大似然方法擬合模型,且在計算代價上二者相當。
本文其余部分安排如下:第1 節介紹了空間權矩陣的具體構造方法、計算機實現以及權矩陣的重要性質;第2 節給出了新的空間滯后模型及其最大似然估計方法;第3 節通過數值模擬實驗驗證了空間權矩陣及其模型擬合方法的有效性;第4 節通過波士頓房屋價格數據分析說明本文方法的實際應用;最后一節是全文的總結與討論,并指出尚需進一步研究的問題。
1 空間權矩陣的構造及其計算機實現
1.1 空間權矩陣的構造及性質
設{si}為n個地理單元所對應的抽樣位置,定義
且~wii= 0(i= 1,2,···,n),則可以得到0-1 值空間權矩陣~W= (~wij)。空間單元鄰接關系可按傳統方法確定,比如對于區域型數據,如果si和sj所對應的區域有公共邊界,那么稱si和sj相鄰;對于點型數據,可用k-最近鄰等方法確定si與sj的鄰接關系,即對每個si,如果sj到si的距離小于或等于si到它第k個最近鄰點的距離,那么si和sj具有鄰接關系。
選擇一個定義域為[0,∞)×[0,∞),值域為[0,1]的二元函數w(d,γ),使滿足:
(i) 給定γ>0,w(d,γ)是d的單調減函數,且limd→∞w(d,γ)=0;
(ii) 給定d>0,有limγ→0+w(d,γ)=0, limγ→∞w(d,γ)=1,且定義w(d,0)=0。
滿足上述條件的函數有很多,如下面兩類函數
對每個a>0 均滿足上述條件(i)和(ii)。
設dij=d(si,sj)為si與sj之間的歐氏距離,也可以是按照實際問題背景所定義的其他距離。將0-1 值權矩陣~W= (~wij)中的“1”用函數值w(dij,γ)替換,即對于1≤i 由函數w(d,γ)的定義及所滿足的條件,可知矩陣W(γ)有如下性質: (i) limγ→0+W(γ) = 0, limγ→∞W(γ) = (diag(~w+))-1~W,即0-1 值權矩陣的行標準化矩陣,其中~w+= (~w1+, ~w2+,···, ~wn+)T是0-1 權矩陣~W各行元素之和所構成的列向量,diag(~w+)為以~w+為主對角元素的對角矩陣; (ii)In-W(γ)對每個γ ≥0 是主對角占優矩陣,從而可逆。 由于W(γ)中已嵌入了其非零元素隨距離下降的控制參數γ,其作用相當于傳統模型(1)中自回歸模型參數ρ,因此在W(γ)下的空間滯后模型為 其中y、X、β、ε與模型(1)中各量的定義相同。 如引言所述,以W(γ)替代模型(1)中的ρW,可以更靈活地反映自變量在任一個目標單元處的觀測值與其鄰接單元處的觀測值的相關性,同時體現了Tobler 地理學第一定律[8]中相關性隨距離下降的一般規律,參數γ將由觀測數據予以估計,因而模型(2)在反映因變量自相關性方面更具自適應性。由W(γ)的性質(i)可知,當γ →0+時,W(γ)→0,這時模型(2)退化為一般線性回歸模型,對應于傳統空間滯后模型(1)中ρ= 0 的情形,即因變量不具有空間自相關性;當γ →∞時,W(γ)趨于0-1 值空間權矩陣的行標準化矩陣,對應于模型(1)中ρ →1 的情形,即因變量正自相關性最強。因此,基于數據適當選擇γ值,可使模型(2)能更自適應地反映因變量的自相關性。 需要指出的是,由于W(γ)的元素均非負,因此模型(2)中的空間自相關項W(γ)y只能反映因變量的正自相關性,即所謂的溢出效應。對空間數據而言,如Griffith[17]所指出的,雖然空間正自相關性普遍存在于實際問題中,但反映競爭效應的空間負自相關性也不應被忽略,也有其存在的許多實例。如果需要探索因變量可能的負自相關性,可在模型(2)中以W(γ)的負矩陣替代W(γ)進行建模分析。另外,在構建W(γ)的過程中,0-1 值空間權矩陣~W是必要的,否則會造成對W(γ)行標準化上的困難。 理論上,傳統的空間滯后模型(1)的各種估計方法都可以推廣到模型(2),而基于最大似然估計的良好性質以及在最大似然估計框架下,模型(1)和模型(2)的估計過程類似,在此僅給出模型(2)中參數γ、β和σ2的最大似然估計方法及其主要步驟。 令A(γ)=In-W(γ),由ε ~N(0,σ2In),可得y的對數似然函數為 其中|A(γ)|為矩陣A(γ)的行列式。對數似然函數分別關于β和σ2求導,并令其等于零,則有 關于β和σ2求解上述方程組,得 將~β和~σ2代入式(3),并略去與γ無關的加項,則得到關于γ的對數似然函數為 利用搜索優化方法,求γ使得l(γ)達到最大,則得γ的最大似然估計?γ,將?γ代入~β(γ)和~σ2(γ)表達式中,則得β和σ2的最大似然估計分別為 本節通過數值模擬實驗,說明權矩陣W(γ)的具體構造過程以及相應空間滯后模型的最大似然估計的有效性。 3.1.1 空間區域及抽樣點 取空間區域為[0,1]×[0,1]的單位正方形,抽樣點按如下兩種方式產生: (i) 15×15 格點區域(樣本容量n=225),抽樣點的空間坐標為 其中mod((i-1)/15)和int((i-1)/15)分別表示i-1 除以15 的余數和整數部分; (ii)n= 225 個服從單位正方形上均勻分布的隨機點,即si= (ui,vi)(1≤i ≤225),其中ui和vi從均勻分布U(0,1)獨立抽取。 具體抽樣點在區域上的分布,如圖1 和圖2 所示。 圖1 格點抽樣 圖2 隨機點抽樣 3.1.2 權矩陣的生成 0-1 值權矩陣~W按如下方式產生:格點抽樣下取Queen 形式(即一個抽樣點所在的小矩形與周圍有公共頂點的小矩形中的抽樣點相鄰);隨機點抽樣下由k-最近鄰方法確定,這里取k=6。w(d,γ)取如下兩種形式: 其中a=0.5,1,1.5,2,d取歐氏距離。 3.1.3 模型及數據產生 考慮如下形式的空間滯后模型 其中各個參數的取值及數據產生方式為: 1)β0=0.5,β1=1.5,β2=-2; 2) 自變量X1和X2的觀測值xi1和xi2(i=1,2,···,n)分別從標準正態分布N(0,1)和(0,1)上的均勻分布U(0,1)中獨立抽取; 3) 誤差項從N(0,1)中獨立抽取,即εi ~N(0,1),i=1,2,···,n; 4)γ=0.05,0.1,0.2,0.4,0.6; 5) 因變量Y的觀測值向量y=(y1,y2,···,yn)T按如下方式產生 其中β=(β0,β1,β2)T,X為設計矩陣,ε為誤差向量。 3.1.4 參數估計精確性度量指標 為降低抽樣誤差對參數估計的影響,對上述的每種情況重復實驗N= 100 次。在此以N次重復下各參數γ、βT和σ2的估計值的均值和標準差來評估參數估計的精確性。以參數γ為例,記N次重復下γ的估計值分別為?γk(k=1,2,···,N),則其均值和標準差分別為 不同情況下的數值模擬實驗結果如表1 至表4 所示。需要指出的是,當給定具體空間數據集時,抽樣點的位置也隨之確定。由于W(γ)中的非零元素與兩兩抽樣點的距離dij(1≤i 表1 格點抽樣且w(d,γ)=exp(-(d/γ)a)時,100 次重復下的參數估計結果 表2 格點抽樣且w(d,γ)=(1-(d/γ)a)+時,100 次重復下的參數估計結果 表4 隨機抽樣且w(d,γ)=(1-(d/γ)a)+時,100 次重復下的參數估計結果 由表1 至表4 中結果可知,γ、β以及σ2的估計值的均值在各種情況下均十分接近于參數的真值。隨著因變量觀測值之間自相關性的增強,即γ值的增加,各參數估計的標準差有增加的趨勢,反映出和傳統空間滯后模型(1)的參數估計類似的特征,即隨著ρ值的增加,參數估計的精度會受到一定影響。但總的來看,各參數估計的標準差變化不大,即自變量自相關性增強對參數估計的精度影響是有限的。上述數值模擬結果反映出在新的空間權矩陣下,模型最大似然估計的有效性。對于更大樣本容量,如n= 400,我們也就一些典型情況進行了模擬實驗,與所預期的一樣,各參數估計的偏差,尤其是標準差均有明顯減小,即估計的精度有明顯提高。 為進一步說明本文所提出的空間滯后模型及其最大似然估計的應用效果,本節將對波士頓房屋價格數據進行分析。該數據集可通過網址http://cran.r-project.org/,從R 軟件包spdep 中下載,其中包含了波士頓506 個普查區1970 年自有住房的中位數價格(MEDV,單位:千美元)和13 個解釋變量在各普查區的觀測值,同時還包括各普查區的直角坐標以及與各個普查區相鄰接的普查區信息。在此,我們選擇Gilley 和Pace[18]基于線性回歸分析表明對MEDV 有顯著影響的9 個解釋變量作為自變量,具體見表5,以MEDV 為因變量建立有關空間滯后模型。 表5 自變量名稱與描述 需要說明的是,原數據集中非洲裔人口比例的取值為經過變換1 000(BK-0.63)2的值,其中BK 為各普查區非洲裔人口每千人的比例。為便于解釋,本文采用的是變換回的數據,即,其中B為原數據集的數值。 利用各普查區的直角坐標可求得506 個普查區兩兩之間的距離矩陣D=(dij)n×n,這里n=506;由各普查區的鄰接關系可得到0-1 值空間權矩陣~W=(~wij)n×n。在此,w(d,γ)仍取為如模擬實驗所示的截尾冪函數和指數函數形式產生的空間權矩陣W(γ) =(wij(γ))n×n,基此擬合如下新的空間滯后模型 為了比較所提出的空間權矩陣在擬合房價空間自相關性的優勢以及對回歸系數估計的影響,在此也擬合了0-1 值行標準化矩陣(記為W0)下的傳統空間滯后模型。同時,我們以兩種模型擬合的殘差向量 在0-1 值權矩陣~W下的MoranI指數[19]為統計量檢驗殘差的空間自相關性,以評估不同空間權矩陣提取因變量空間自相關性的能力以及模型的擬合效果,其中以MoranI分布的正態逼近求雙邊檢驗的p值。在兩種生成空間權矩陣的函數w(d,γ)下,我們嘗試了其中參數a的多個取值,通過MoranI檢驗結果各選擇了三種情況,連同在W0下傳統空間滯后模型的估計結果列于表6 中。 表6 不同空間權矩陣下各模型的擬合結果 由表6 結果可知,不同的空間權矩陣的確對回歸系數的估計有較大的影響,說明在實際應用中選擇恰當的空間權矩陣是很重要的。但就表6 結果而言,除CRIM 和DIS 外,各自變量系數估計的正、負號均一致,因而從定性角度解釋自變量對房價的影響會得出一致的結論。但從MoranI檢驗結果看,基于行標準化的0-1 值空間權矩陣的傳統空間滯后模型顯然未能較好地擬合房屋價格數據的空間自相關性(殘差的MoranI檢驗p值為0.001 5),而本文所構造的空間權矩陣下的空間滯后模型在擬合因變量空間自相關性方面可以通過選擇w(d,γ)的適當形式,得到更為滿意的結果。 基于MoranI檢驗結果以及各解釋變量的實際意義,基于截尾冪函數w(d,γ) =(1-(d/γ)a)+所生成的三種權矩陣下的空間滯后模型均是較合理的分析波士頓房屋價格數據集的可選擇模型。與傳統的空間滯后模型的估計結果相比,自變量DIS 的系數估計值變化較大,甚至在a等于0.4 和0.5 時,估計值出現了反號的情況。但由數據集可知,有些普查區(如370~374 號)DIS 的值很小(在1.1~1.4 之間),但房價中位數MEDV 達到最高的5 萬美元;也有一些普查區(如192~205 號)DIS 的值均較大(在6.0~7.7 之間),且MEDV 的值也明顯偏大(4 萬美元左右)。其實,Li 等[20]通過擬合空間自回歸變系數模型,基于所提出的Bootstrap 檢驗方法得到DIS 的系數隨空間位置顯著變化,即是一個空間變系數,且系數估計值在大部分普查區都為正值。而本文兩種模型下的系數估計可以看作是平均意義下的估計值,同時考慮到傳統空間滯后模型未能充分擬合房價的自相關性,而在新的空間權矩陣下,當房屋價格間的自相關性通過W(γ)y項充分擬合后,在平均意義下DIS 與MEDV 呈現正相關是有可能的,或者這時DIS 對MEDV 的影響會變得不顯著,但這需要進一步建立在本文所提出的空間滯后模型下參數顯著性的檢驗方法。 本文基于0-1 值空間權矩陣,構造了含有控制參數的距離衰減空間權矩陣,建立了新的空間滯后模型,給出了模型的最大似然估計方法。數值模擬實驗表明了其最大似然估計的有效性;實例分析表明所構造的空間權矩陣能更有效擬合因變量的空間自相關性,并且能通過某些模型診斷準則,嘗試多種形式的空間權矩陣,選擇出更合理的模型。另外,和基于機器學習技術選擇空間權矩陣的方法相比,本文構造的空間權矩陣不僅反映了Tobler 地理學第一定律的要旨,而且由于其中參數的明確意義,使其更具可解釋性。 本文利用MoranI指數為模型診斷統計量,從殘差自相關顯著性角度在實際應用中選擇更合理的模型,其他如均方誤差準則、似然函數準則以及AIC 準則等擬合優度準則均可作為實際應用中模型的選擇標準。需要指出的是,本文只給出了空間權矩陣的構造以及相應空間滯后模型的最大似然估計方法,相關統計推斷問題仍需要進一步研究。與傳統的空間滯后模型不同,新的空間滯后模型將其中的自相關強度參數ρ變為了距離衰減的控制參數γ,納入在權矩陣元素中,導致相應對數似然函數關于各參數的信息矩陣不再有顯式表示,因而傳統空間滯后模型下關于參數顯著性的似然比檢驗、Wald 檢驗以及Lagrange 乘子檢驗等不能直接應用于新的空間滯后模型,但通過Bootstrap 方法實現對參數的檢驗似乎是一條可行的途徑,這也是我們接下來的主要研究工作之一。1.2 空間權矩陣構造的計算機實現
2 以W(γ)為空間權矩陣的空間滯后模型及其估計
2.1 空間權矩陣W(γ)下的空間滯后模型
2.2 模型(2)的最大似然估計
3 數值模擬實驗
3.1 實驗設計
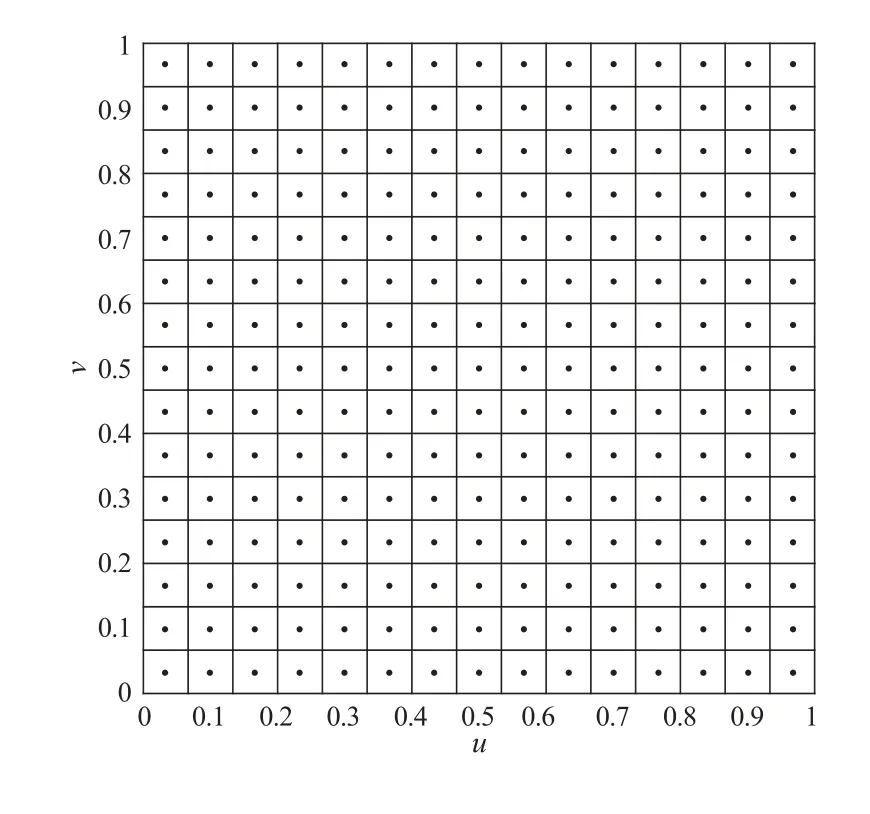

3.2 實驗結果及分析
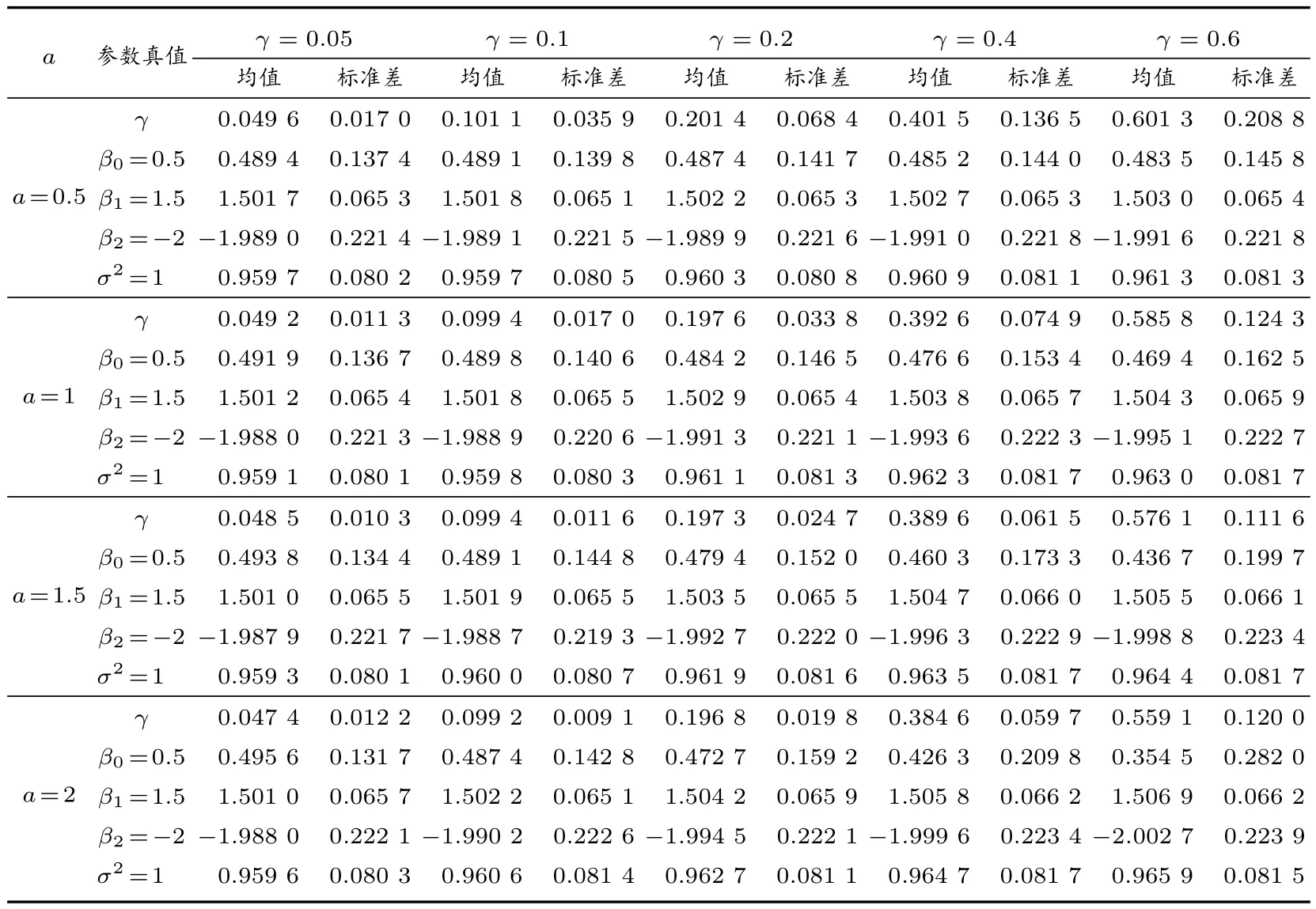
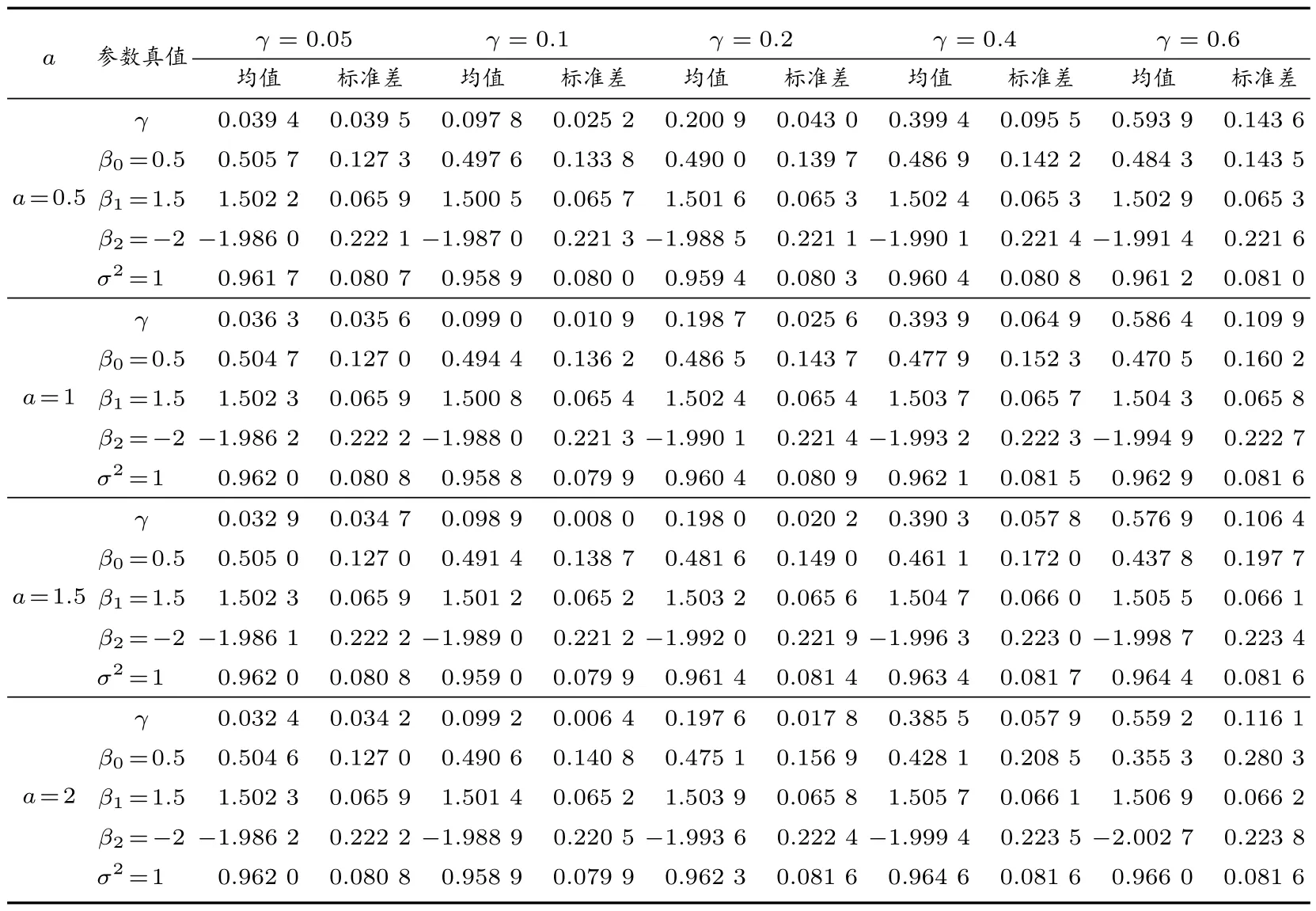

4 實例分析

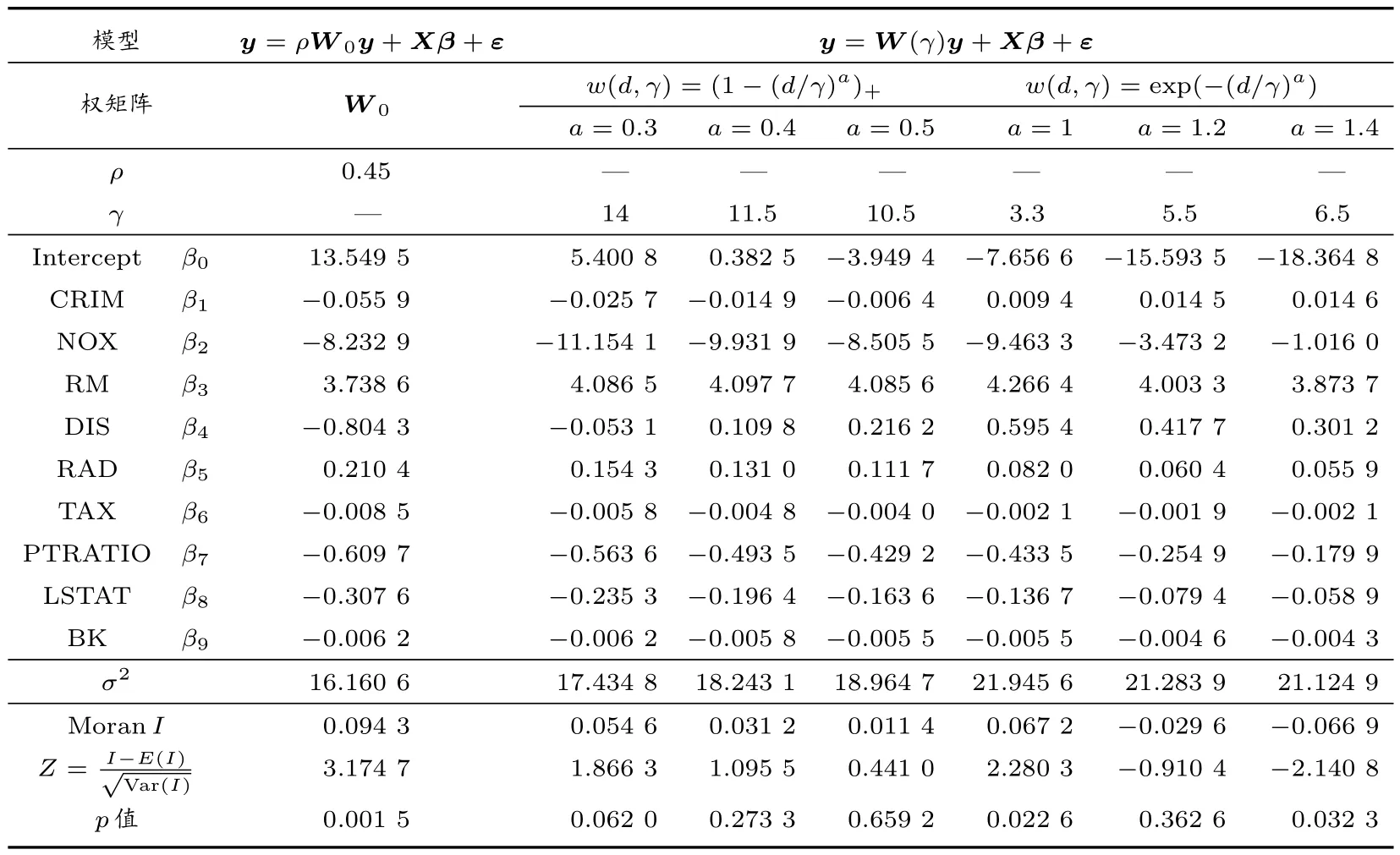
5 總結與討論

