改進PM 算法數值求解常微分方程邊值問題

謝正榮, 艾軼博, 張衛冬,

(1.北京科技大學國家材料服役安全科學中心，北京 100083;2.華東師范大學數學科學學院，上海 200241)

0 引言

文獻[1]利用微分方程殘差將常微分方程初值問題的數值求解過程轉化為一個優化問題，在梯形數值積分公式的基礎上，引入彈性梯度下降法優化參數求得符合精度要求的數值解。本文將其稱作PM 算法，該算法基本流程如下：首先在各積分節點處設置二元參數對{wk,bk}，獨立地線性逼近該節點處的最高階導函數；隨后，從最高階導函數層開始逐階向上使用復化梯形求積公式數值積分至解函數層；最后，基于微分方程的殘差，迭代優化參數對{wk,bk}。

PM 算法與僅用于求解線性常微分方程初值問題的同類工作[2–3]相比，具有精度高、收斂速度快的優點；而基于循環神經網絡的強大逼近能力，PM 算法尤其適用于高階非線性常微分方程初值問題的數值求解。此外，與文獻[4—5]中純網絡型結構的試解相比，PM 方法可嚴格滿足初值條件；而由文獻[6]可知，文獻[4—5]的方法中，邊界誤差與域內殘差存在競爭關系，故無法嚴格滿足初值條件。

值得注意的是，原始PM 算法雖有上述優勢，但它無法解決常微分方程的邊值問題：欲啟動第k階梯形求積過程，則需要該階導函數的初值，即y(k)(x0)，否則只能計算各區間內的增量。由于邊值問題并不能夠提供足夠的初值條件，這便導致了此算法無法求解邊值問題。以二階常微分方程兩點邊值問題I 型邊界條件為例

無法完成，進而導致整個求解過程失敗。

為將原算法推廣至邊值問題求解，本文作出如下4 點改進：

1) 提出“分離原理”，使得PM 算法可在一階常微分方程組形式下使用，從而為PM 算法求解二階常微分方程兩點邊值問題提供理論基礎。具體地，選取狀態量將其轉化為一階常微分方程組，隨后基于分離原理分別訓練邊界誤差和域內殘差；

2) 在一階常微分方程組架構中發現了二階常微分方程I/II 型邊值問題在計算格式上的等價性；

3) 在參數集不變的前提下，利用現有參數，保持導數關系，假設缺失的初值條件，結合分離原理，實現PM 算法求解常微分方程I/II 型邊值問題，簡記為“導數法”；

4) 引入額外參數補充缺失的初值條件，結合分離原理，實現PM 算法求解常微分方程I/II/III 型邊值問題和混合型邊值問題，以下簡記為“增參法”。

最后，通過針對邊值問題的數值實驗測定了PM 算法的收斂階(2 階收斂)。

關注常微分方程兩點邊值問題數值求解的文獻通常僅僅只是針對I 型邊界條件展開理論推導、提出對應的專門化的解決方案，例如文獻[7—12]。但一般而言，III 型和混合型邊值問題的數值求解難度明顯大于I 型問題。本文提出的“增參法”是直接面向III 型和混合型邊界條件的，且同時兼容I/II 型問題。此外，本文在一階常微分方程組形式下發現了I/II 型邊值問題在計算格式上的等價性，此發現有助于將已有的I 型邊界條件處理方式直接應用于II 型問題，提高算法代碼復用率。

1 預備知識

原始PM 算法求解單個常微分方程初值問題的基本原理如下。

由于g(xi)和g′(xi)無法直接獲得準確值，且不同積分節點處g(xi)和g′(xi)的值不同，即線性主部的斜率和截距隨積分節點變化，故考慮為不同積分節點處的線性主部選取不同的可調二元參數對(wi,bi)，并通過優化技術不斷調整{(wi,bi)}mi=0，以使得

此即為二元參數對(wi,bi)的數學解釋。

(ii) 若待求函數僅n階可導，則(wi,bi)不可作如上理解。但是從積分角度而言，g(x)不夠光滑并不影響對其作梯形數值積分，故PM 算法仍然有效。因此，(i)中的解釋可看作是“最高階導函數離散線性參數化”的思想來源。

2 分離原理：改進PM 算法處理邊界條件的理論基礎

PM 算法求解邊值問題時，除需要收斂計算域內各處的微分方程殘差外，還需要極小化邊界誤差，故此時的目標函數將重構為一個多目標優化問題。事實上，將PM 算法應用于一階常微分方程組初值問題求解時，每一個分量方程都存在一個微分方程殘差向量，此時的目標函數同樣需要把多個微分方程殘差向量同時約束在內。因此，不妨先考慮如何改進原始的PM 算法以求解一階常微分方程組初值問題，隨后便可將相同的原理作用于高階常微分方程/一階常微分方程組邊值問題求解了。以三元一階常微分方程組初值問題為例，其一般形式如下

因為目標函數中存在三個誤差對應的三個優化項，屬于多目標規劃。因此，引入λ1、λ2和λ3三個比例系數以表示各個優化項的重要程度。根據文獻[13]的推導思路，基于李雅普諾夫穩定性理論易得，原始PM 算法收斂的一個充分性條件為

于是，便將一個多目標規劃問題轉化為三個相對獨立的單目標規劃問題加以求解，每一個單目標規劃問題即可按照前文的推導方法獲得屬于自己的獨立的自適應學習速率，然后用最速下降法實現極小化。此時權值、偏置值更新規則如下

增量式(11)右邊第一項表示基于目標函數J1所作的迭代優化，之后兩項以此類推。雖然分離原理告訴我們可以獨立地極值化三個目標函數，但由于三個目標函數擁有完全相同的自變量，即所有權值、偏置值，故每一個目標函數都會對所有權值、偏置值作更新。因此，從權值、偏置值角度看，在每一步迭代中，每一個權值、偏置值的增量是所有殘差分量引起的多個增量之和。

為強調分離原理本質上仍然是在對所有分量式誤差以及可能的邊界誤差的極小化作綜合平衡性考慮，即仍然處理的是多目標規劃問題，在后文敘述中常微分方程組的目標函數仍取為等價重構前的加權平方和格式。

現對分離原理的數學本質作出說明：取

其中F=R,D,E,l=1,2,3，則有簡化形式

現考慮二階常微分方程邊值問題，只需要將邊界誤差EBC視作額外增加的又一個微分方程殘差分量，即由{R,D}擴張為{R,D,EBC}即可。顯然{R,D,EBC}形式上等價于{R,D,E}，從而符合上述分離原理范式，故可使用已有的等效學習速率計算公式基于最速下降法同時分別訓練域內殘差和邊界誤差。邊界誤差的權重系數及其在逐次處理方案下的等價形式將在第3 節中詳細說明且適用于后文所有求解邊值問題的章節內容。

3 改進PM 算法數值求解常微分方程(組)邊值問題

以二階常微分方程為例，邊值問題描述為r′′=F(t,r,r′),t ∈[t0,tN]。I 型邊界條件r(t0)=α,r(tN)=β；II 型邊界條件r′(t0)=α,r′(tN)=β；III 型邊界條件

借鑒打靶方法試探性假設缺失的初值，將邊值問題轉化為初值問題再加以數值求解這一思路，結合PM 算法自身特點，針對性地提出了兩種假設初值的方案：保持導數關系假設初值(導數法)；引入新參數假設初值(增參法)。轉化為初值問題后再用PM 算法求解。

值得注意的是，PM 算法求解邊值問題需要額外引入邊界誤差EBC訓練參數調整假設的初值條件。因此，目標函數將由微分方程殘差Ri和邊界誤差EBC兩部分組成，二者權重分配參考文獻[6,14]分別取λin=1,λBC=10。保證其收斂的自適應學習速率的推導將用到前文提出的分離原理，以分別保證上述兩類誤差各自收斂最終使得目標函數極小化。為方便，按逐次處理方案進行編程，我們對邊值問題目標函數作如下等價變形

這一等價變形適用于下文所有涉及邊界誤差訓練的情況，后文敘述中將省略。

為將II 型邊值問題轉化為I 型邊值問題加以求解，后文所有討論均在一階常微分方程組形式中展開，理由詳見3.1 節。但需要說明的是，本文提出的導數法與增參法亦可在單個二階常微分方程形式下作類似推導構造出相應的處理方案。

3.1 二階常微分方程I/II 型邊值問題在一階常微分方程組形式下的計算格式等價性

對于二階常微分方程邊值問題，I 型邊界條件與II 型邊界條件在其一階微分方程組形式下等價。

二階常微分方程I 型邊界問題

令x=r,y=r′，可得如下二元一階常微分方程組

即

一般形式的二元一階常微分方程組的I 型邊界問題如下

對比式(20)、式(23)和式(24)可知，二階常微分方程的I 型邊界問題的微分方程組形式和二階常微分方程的II 型邊界問題的微分方程組形式均是二元一階常微分方程組的I 型邊界問題的特例，故構造求解二元一階常微分方程組I 型邊界問題的算法即可同時滿足求解二階常微分方程I 型邊界問題的和II 型邊界問題的需求。所以，對于二階常微分方程II 型邊值問題，首先將其轉化為一階常微分方程組II 型邊值問題形式，然后用一階常微分方程組I 型邊值問題的求解算法即可。基于此，后文中我們僅在二元一階常微分方程組形式下展開討論。

3.2 導數法求解一階常微分方程組I/II 型邊值問題

以此類推下去。注意，由于只是作近似處理，為避免引入更多的待定參數，故可省去各階積分常數。按照上述規律類推，可到達0 階導函數層即解函數層，再令i= 0，即可利用現有參數試探性補充邊值問題中缺失的某個初值條件。由于上述類推格式存在逐階求導關系，故稱為導數法。

以二元一階常微分方程組為例，注意到方程組第二個分量式缺少一個初值條件，不妨假設

1) 計算域內微分方程殘差訓練

當i=0 時，有

2) 邊界誤差訓練

感興趣的讀者可以嘗試在單個二階常微分方程形式下寫出EBC的表達式，并與式(35)做對比可知，將高階微分方程轉換為一階常微分方程組形式再加以數值求解，往往可以簡化計算，得到更為簡潔的公式結果。

注意，上述公式表明EBC與第二分量式的參數U和V無關，僅取決于第一分量式的參數W和b，即

算例1 的參數配置見表1 和表2，求解精度見表3。

表1 算例1 導數法改進PM 算法的參數配置

表2 算例1 導數法改進PM 算法的參數配置

表3 算例1 導數法改進PM 算法的求解精度

算例2 的參數配置見表4，求解精度見表5。

表4 算例2 導數法改進PM 算法的參數配置

表5 算例2 導數法改進PM 算法的求解精度

3.3 引入獨立參數試探初值條件

引入新參數假設初值，新參數相當于擴充微分方程殘差的自變量維度，對于二階常微分方程即有

因此，對于計算域內微分方程殘差的訓練，只需額外求解與新引入參數相關的梯度。然后，相應地對引入新參數前的等效學習速率公式補充相關項，即可沿用求解初值問題的程序代碼。

與保持導數關系假設初值條件方法相比較，引入與舊參數集{w,b}無關的、獨立的參數p和q補充初值條件，可以避免引入二次項增加公式復雜度和計算量，本文稱此方法為增參法。

3.3.1 增參法求解一階常微分方程組I/II 型邊值問題

對于如下二元一階常微分方程組

權值偏置值的更新規則如下

1) 計算域內微分方程的殘差訓練

基于分離原理，易得計算域內各分量式的自適應學習速率

所以，與常微分方程組初值問題中的G1和G2相比較，有如下關系

其中G1和G2參見式(32)和式(33)，即引入獨立參數試探初值條件方案中的域內殘差與3.2 節的第1)小節中保持導數關系假設初值條件方案中的域內殘差是一致的。于是，有

基于此，在二元一階常微分方程組初值問題求解程序中，補充相關梯度、修正自適應學習速率后，即可直接用來求解二元一階常微分方程組邊值問題。

2) 邊界誤差訓練

注意，上述公式表明，新引入的參數p和q不參與EBC的計算，且EBC與第二分量式的參數U和V無關，僅取決于第一分量式的參數W和b，即EBC=EBC(W,b)。由于分量式是一階微分方程，所以計算EBC只需經過一次梯形求積分。這再一次表明，數值求解時，將高階常微分方程轉化為一階常微分方程組再進行求解會更加簡潔。

基于此，易知引入新參數試探初值條件方案中的?EBC/?W和?EBC/?b與保持導數關系試探初值條件方案中的?EBC/?W和?EBC/?b完全一致，從而邊界處自適應學習速率計算公式亦保持一致，故此處不再贅述，所需梯度值及邊界處自適應學習速率詳見3.2 節中第2)小節。

算例3 懸鏈線方程[15]

I 型邊界條件y(0)=1,y(5)=3.282 557。以Matlab 的bvp4c 命令所得數值解為參考。

設u=y,v=y′，則有

算例3 的參數配置如表6，分量式權重和邊界誤差權重見表7，表8 給出了求解精度。

表6 算例3 增參法改進PM 算法的參數配置

表7 算例3 增參法改進PM 算法的分量式權重和邊界誤差權重

表8 算例3 增參法改進PM 算法的求解精度

算例4[16]r′′=-r+2r′+t,t ∈[-2,1]。II 型邊界條件r′(-2)=0.594,r′(1)=1。解析解r=(t-2)et+t+2。

取u=r,v=r′，一階常微分方程組形式為

算例4 的參數配置見表9，求解精度見表10。

表9 算例4 增參法改進PM 算法的參數配置

表10 算例4 增參法改進PM 算法的求解精度

3.3.2 增參法求解一階常微分方程組III 型邊值問題

對于如下的二元一階常微分方程組

1) 計算域內微分方程殘差訓練

記

算例5 的參數配置見表11，求解精度見表12，求解結果如圖1 所示。

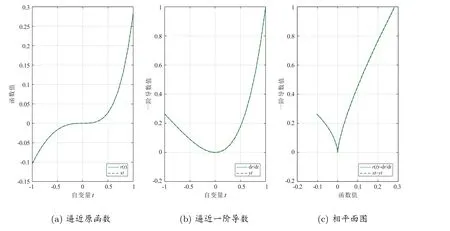
圖1 算例5 增參法改進PM 算法的求解結果

表11 算例5 增參法改進PM 算法的參數配置

3.3.3 增參法求解一階常微分方程組混合型邊值問題

設有二階常微分方程r′′=φ(t,r,r′),t ∈[t0,tN]。三類邊界條件的統一形式如下

其中α0α1≥0,β0β1≥0。

對于二元一階常微分方程組，則有

其中α0α1≥0,β0β1≥0。

易知，當α0=β0= 0 且α1?= 0,β1?= 0 時，即為I 型邊值條件，當α1=β1=0 且α0?= 0,β0?= 0 時，即為II 型邊值條件，當α1=β1= 1 且α0> 0,β0> 0 時，即為III 型邊值條件。

當然，兩端點處的邊值條件可以是不同類型。例如：當α1?= 0,α0= 0,β1=0,β0?=0 時，t=t0處則為I 型邊值條件，t=tN處則為II 型邊值條件。如此，便是一個混合型邊值問題。

記x(t)和y(t)為微分方程組的真實解。xt(t)和yt(t)為PM 算法所求得的微分方程組的近似解。xt(ti)和yt(ti)簡記為xi和yi。x′(ti)的近似值x′t(ti)，簡記為x′i，設x′i=wixi+bi,i= 0,1,···,N。y′(ti)的近似值y′t(ti)，簡記為y′i，設y′i=uixi+vi,i=0,1,···,N。

記W= [w0,w1,···,wk,···,wN]T,b= [b0,b1,···,bk,···,bN]T,U= [u0,u1,···,uk,···,uN]T,V= [v0,v1,···,vk,···,vN]T。注意方程組第缺少x(t0)和y(t0)兩個初值條件，設

其中θ=W,b,U,V,μ,τ,p,q。

1) 計算域內微分方程殘差訓練

記

同理可得

2) 邊界誤差訓練

算例6r′′=-r+2r′+t,t ∈[-1,1]。混合邊界條件如下，當t=-1 時，II 型邊界條件-r′(-1) =-0.264 24。當t= 1 時，III 型邊界條件r(1)+r′(1) = 1.281 7。解析解r=(t-2)et+t+2。

取x=r,y=r′，一階常微分方程組形式為

算例6 的參數配置見表13，求解精度見表14，求解結果如圖2 所示。

圖2 算例6 增參法改進PM 算法(逐點配置η)的求解結果

表13 算例6 增參法改進PM 算法的參數配置

表14 算例6 增參法改進PM算法的求解結果

4 PM 算法的收斂階

采用文獻[12]的做法，通過針對邊值問題的數值實驗來比較本文PM 算法與傳統的迎風格式和中心差分格式的收斂階

微分方程

I 型邊界條件u(0)=0,u(1)=0，解析解u=sin(πt)。

取x=u,y=u′，一階常微分方程組形式為

邊界條件處理方案選用3.3 節中的增參法。迭代精度10-10，允許最大訓練次數5 500，分量式與邊界誤差權重λ1=λ2= 1/2,λBC= 10。收斂階的實驗結果見表15。

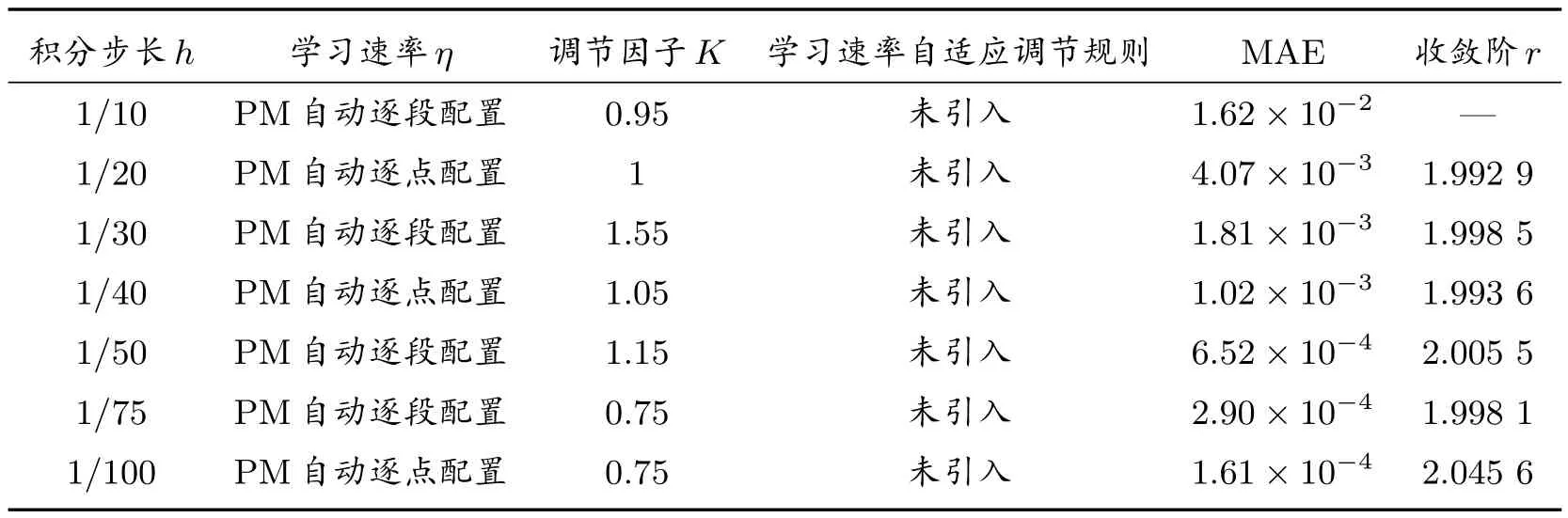
表15 PM 算法的收斂階

已知迎風格式是1 階收斂，中心差分格式是2 階收斂，本文改進的PM 算法收斂階為2 階。

5 總結

本文首先介紹了現有文獻中PM 算法的基本原理和計算過程，隨后考慮到將高階常微分方程轉化為一階常微分方程組進行求解是傳統遞推型數值解法的常規預處理方式，有利于計算的范式化和推廣，故為在常微分方程組形式下使用PM 算法，提出分離原理將微分方程組對應的多目標優化問題轉化為多個相對獨立的單目標優化問題。PM 算法的前向計算過程依賴于復化梯形求積公式的遞推型數值解法，因此在求解初值條件缺失的兩點邊值問題時該算法失效。為將該算法推廣至邊值問題求解，借鑒試射法的思想，結合PM 算法的特點，提出了保持導數關系試探初值條件和引入獨立參數試探初值條件兩種解決方案，并基于提出的分離原理引入邊界誤差訓練，這兩種方法在求解邊值問題時均取得了較好的效果；最后，通過針對邊值問題的數值實驗測得改進后的PM 算法的收斂階為2 階。