長度偏差完全數據下均值剩余壽命的矩類估計
武洪萍
(山東石油化工學院大數據與基礎科學學院,東營 257061)
0 引言
均值剩余壽命又稱為期望壽命,是指系統或個體在已生存時間t后還能繼續生存的壽命期望。這一概念在生物醫學等諸多實踐領域中發揮著重要作用。目前,關于均值剩余壽命的統計推斷已經出現了很多研究結果。例如,Yang[1]在完全樣本下提出了均值剩余壽命的非參數點估計;當壽命數據為右刪失時,Kumazawa[2]提出了均值剩余壽命的一致估計;對于左截斷右刪失樣本,Zhao 等[3]以生存函數的左截斷乘積限估計為基礎,發展了均值剩余壽命的非參數估計;而Wu 和Shan[4]則在長度偏差右刪失樣本下研究了均值剩余壽命的矩類估計。另外,對于長度偏差完全樣本,Fakoor[5]以感興趣總體分布函數的經驗估計為基礎,發展了均值剩余壽命的經驗估計。類似于文獻[5]中的研究工作,本文將主要致力于研究長度偏差完全樣本下均值剩余壽命的矩類估計。
長度偏差數據就是平穩性假設前提下的左截斷數據,這也就意味著在長度偏差數據中個體對應的生存時間被納入樣本的概率與它的長度成正比。已有文獻中除了對長度偏差數據進行描述之外,也討論了其統計推斷。例如,Luo 和Tsai[6]提出了生存函數的兩種偽部分似然點估計,但是這種偽似然方法處理起來比較困難。因此,Huang 和Qin[7]在長度偏差右刪失樣本下對左截斷P-L 估計[8]進行了改進,得到了生存函數的乘積限類估計。另外,為了在刪失長度偏差數據下估計分位數剩余壽命,Wang 等[9]提出了以模型為基礎的非參數和半參數估計方法,并將它們用于分析癡呆癥患者的分位數剩余壽命。Shi 等[10]則在刪失長度偏差數據下分析了分位數的非參數估計。對于有協變量出現的半參數模型,也已出現很多的研究結果。例如,為了分析Cox 模型中的參數效應,Qin 和Shen[11]及Huang 和Qin[12]分別在長度偏差數據下提出了模型的矩法估計方程和復合估計方程;而Bai 等[13]和Wu 等[14]則分別研究了比例均值剩余壽命模型和加性均值剩余壽命模型的估計方程。
長度偏差數據在壽命研究廣泛存在,但是在長度偏差完全樣本下對均值剩余壽命的研究卻很少。因此,本文重點研究均值剩余壽命在長度偏差完全數據下的非參數估計及其漸近性質。在估計過程中,利用目標總體和長度偏差變量之間的關系,通過消除均值剩余壽命函數中總體均值這一冗余參數的影響,建立目標參數的矩類估計。同時,也證明了估計量的大樣本性質,并通過數值模擬研究其在有限樣本下的性質。
1 符號假設
設T0表示某感興趣系統或個體的壽命長度,而A0為作用于T0的左截斷時間,兩者非負且獨立。在左截斷抽樣機制中,當且僅當A0≤T0時,個體的壽命長度才能被觀測到。因此,為保證部分個體的壽命長度是可以被觀測的,需假定左截斷概率α= Pr(A0≤T0)> 0。令A和T分別表示可觀測的左截斷時間和壽命長度,則可觀測數據對(A,T)的概率分布與(A0,T0)在給定條件A0≤T0時的條件概率分布相同。若A0的概率分布為均勻分布,那么在左截斷抽樣下得到的可觀測變量T是一個長度偏差變量。

而長度偏差變量T的密度函數為
由(1)式,可得
同樣,可得A和V享有相同的概率密度,即
根據均值剩余壽命函數的定義,感興趣生存時間T0在給定時刻t ∈[0,τ)的均值剩余壽命為
或
當t ≥τ時,m(t)=0。
2 估計方法
不妨設(Ai,Ti),i=1,2,···,n,是來自(A,T)的一個簡單隨機樣本。Fakoor[5]在(1)式基礎上將T0的分布函數F表達為

而當t ≥T(n)時,︿mn(t)=0。
顯然,在上述估計過程中,沒有考慮消除冗余參數μ的影響。為此,我們提出m(t)在長度偏差完全數據下的另外兩種非參數估計。
2.1 估計方法I
結合(1)式和(4)式,隨機變量T0在給定時刻t ∈[0,τ)的均值剩余壽命可以表示為
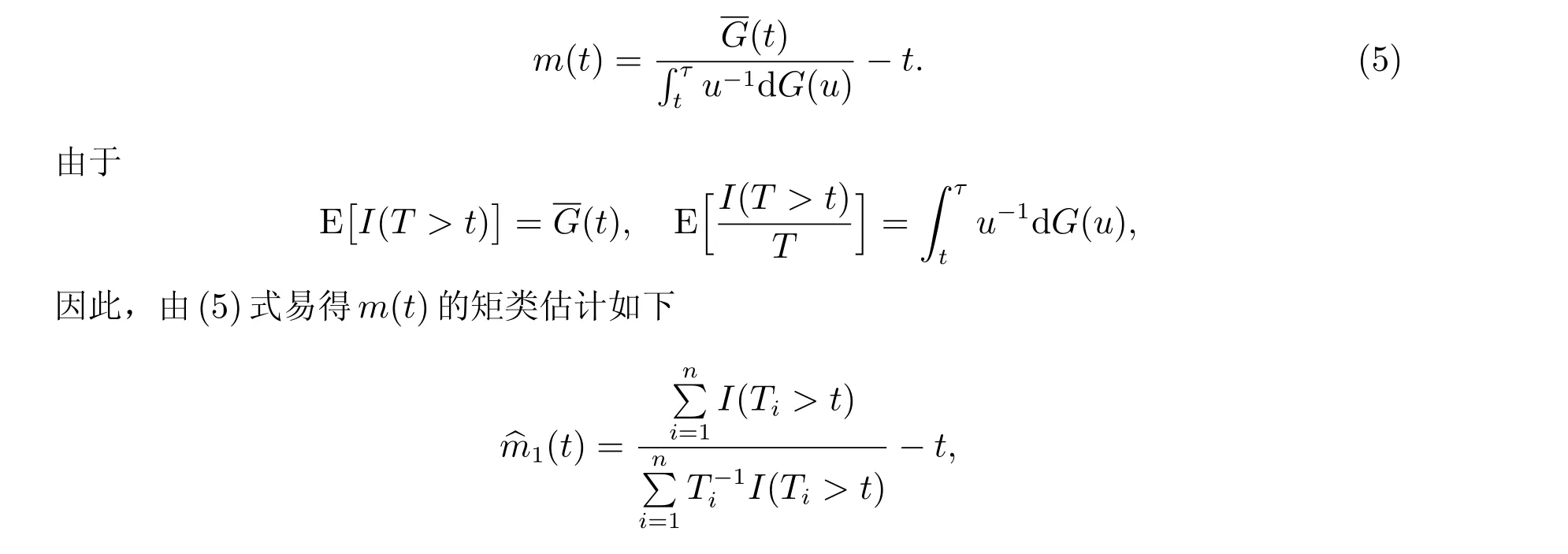
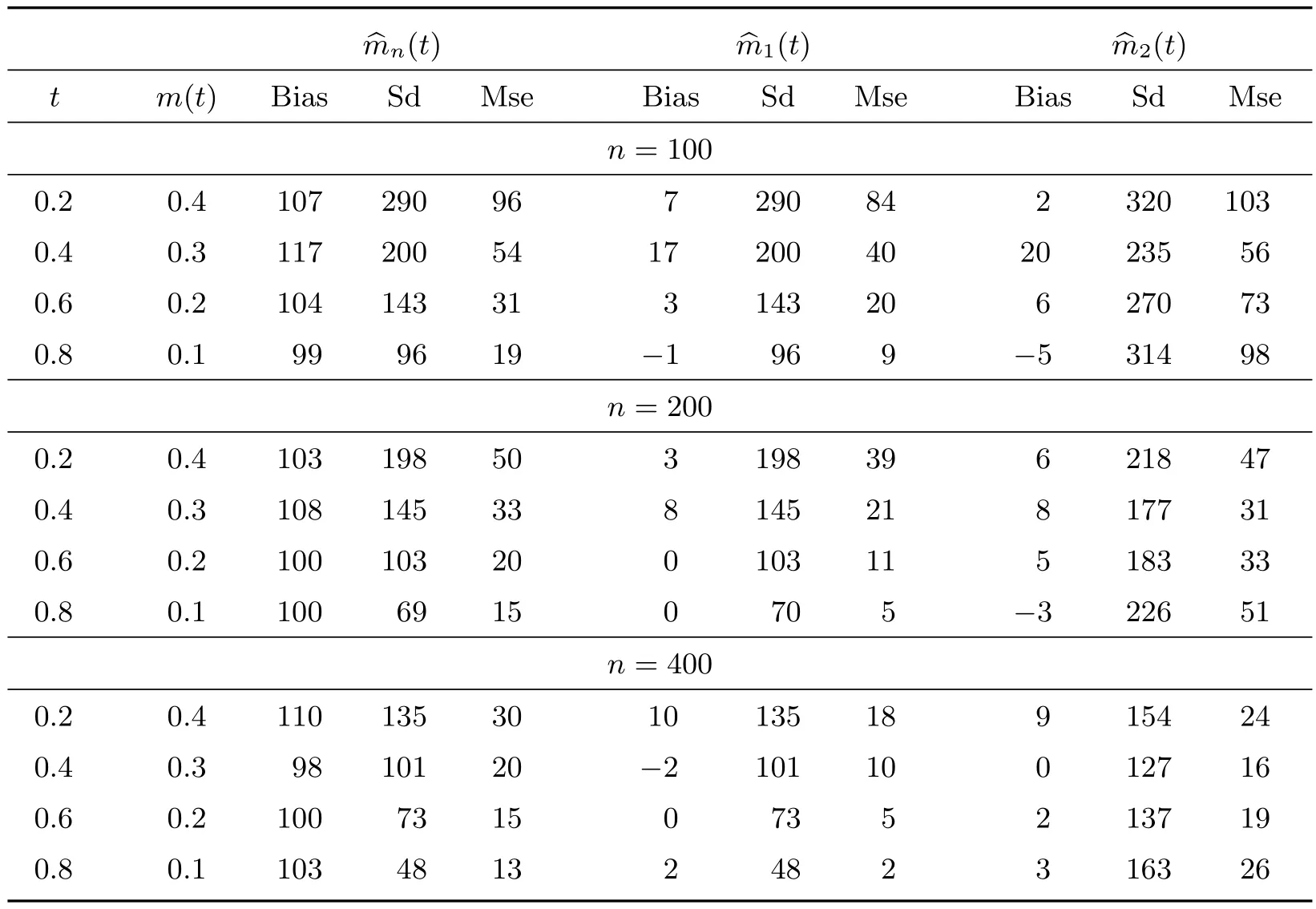
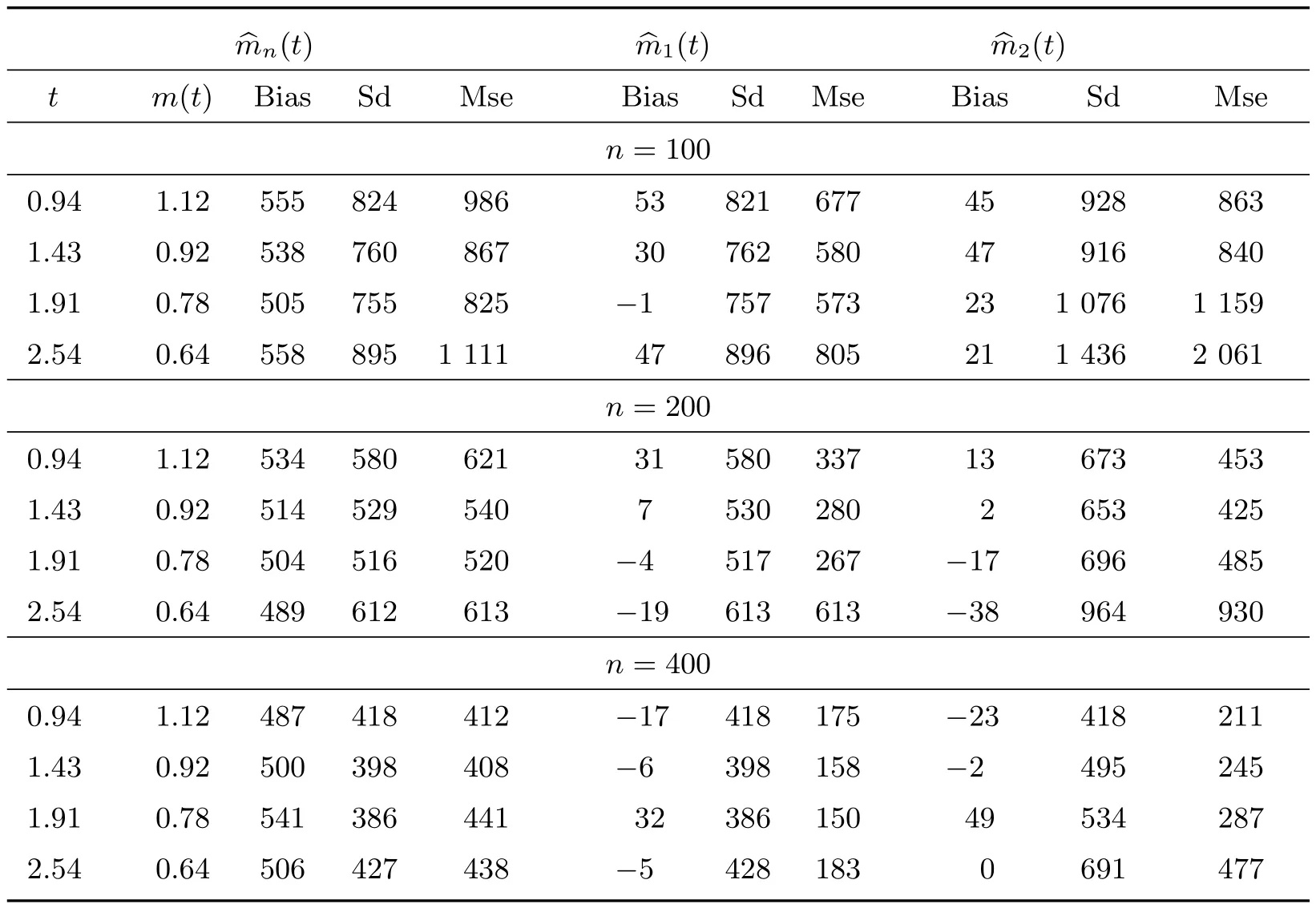
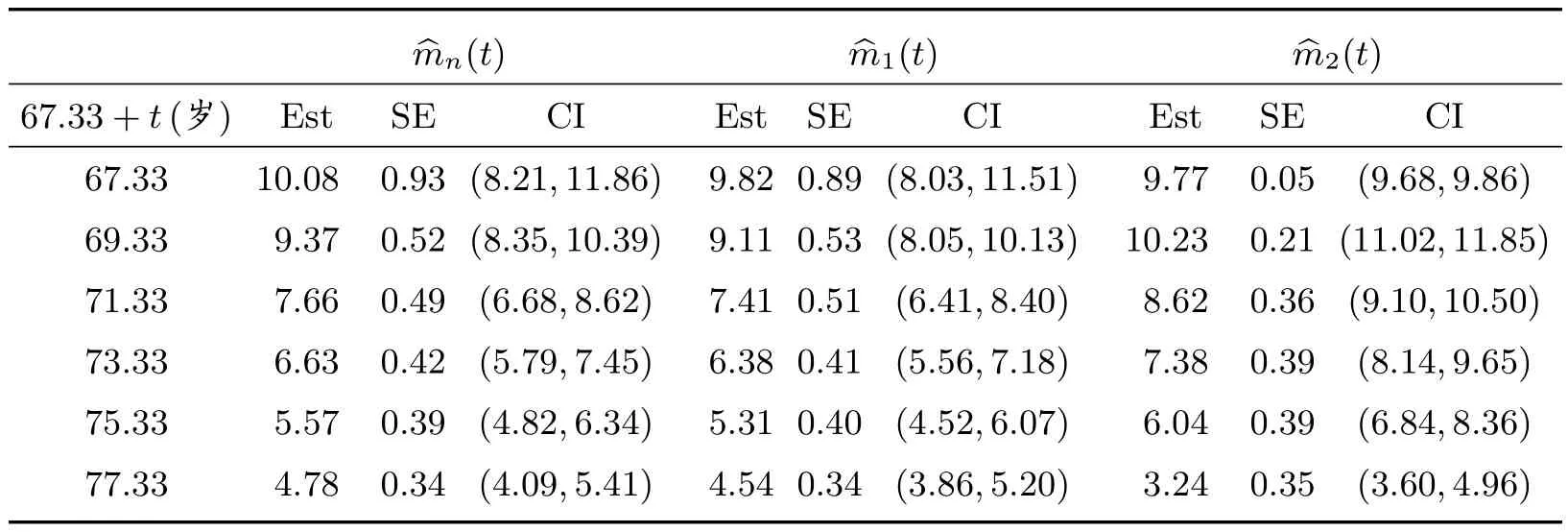
這里0≤t 結合(2)式和(3)式可知,隨機變量T0在時刻t的均值剩余壽命又可表示為 這里SA(t)表示隨機變量A的生存函數,故易得其經驗估計為 在長度偏差抽樣機制下,A和V享有相同的概率分布;直觀上講,結合A與V的信息能夠提升SA的估計精度。由于 故可得SA(t)的復合經驗估計如下 從而,根據(6)式可得m(t)的另一矩類估計 其中0≤t 假設下列條件成立: (C1)L是一非負常數,且滿足0 (C2)S在[0,L]上絕對連續; (C3) 0<μ=ET0<∞, Var(T0)<∞。記根據中心極限定理,可得如下結論。 引理1 若條件(C1)~(C3)及(7)式成立,那么對任意的t ∈[0,L],當n →∞時,有: 為了評價上述兩個估計量的優劣,我們考慮兩種方案進行模擬試驗。在模擬過程中,樣本容量n分別取100、200 和400 三種情況,且每次模擬試驗重復的次數均為1 000。 方案I 感興趣總體T0~U(0,1),左截斷變量A0~U(0,100)。重復產生(A0,T0)的隨機數,直到有n組滿足約束條件A0≤T0的數據為止。用︿mn(t)、︿m1(t)及︿m2(t)分別估計T0在t等于0.2、0.4、0.6 和0.8 時的均值剩余壽命。易知,在這四個點處,T0的生存概率分別為0.8、0.6、0.4 和0.2,且均值剩余壽命的真值分別為0.4、0.3、0.2 和0.1。模擬結果總結在表1 中,其中Bias=經驗偏差×104,Sd=經驗標準差×104,Mse=經驗均方誤差×105。 表1 方案I 中模擬結果比較 方案II 感興趣總體T0服從威布爾分布,對應的生存函數為S(t)=exp(-t2/4),且左截斷變量A0~U(0,100)。類似于方案I,重復產生n組滿足約束條件A0≤T0的隨機數據對(A0,T0)。用︿mn(t)、︿m1(t)及︿m2(t)分別估計T0在t等于0.94、1.43、1.91 和2.54時的均值剩余壽命。在這四個點處,T0的生存概率也分別為0.8、0.6、0.4 和0.2。均值剩余壽命m(t)在上述點處的真值分別為1.12、0.92、0.78 和0.64。模擬的數值結果總結在表2 中,其中Bias、Sd、Mse 的含義與表1 中的相同。 表2 方案II 中模擬結果比較 從表1 和表2 中的數值結果可以看出,三種方法所產生的經驗偏差都比較小。除此之外,還可以得到如下結論; 1) 在兩種方案中,由︿mn(t)模擬產生的經驗偏差相對較大,而另外兩種方法產生的經驗偏差都很小; 2) 從經驗標準差的角度來看,三種方法中︿m2(t)產生的經驗標準差相對較大,而︿mn(t)和︿m1(t)產生的經驗標準差非常接近。三種方法所對應的經驗標準差都隨樣本容量的增大而越來越小; 3) 雖然︿m1(t)與︿mn(t)產生的經驗標準差大小很接近,但是從經驗均方誤差的角度來看,︿m1(t)所產生的經驗均方誤差要比︿mn(t)的小得多,這在方案II 中尤其明顯。當然,隨著樣本容量的逐漸增大,它們對應的經驗均方誤差也是逐漸減小。 綜上可以看出,當樣本容量n和時間點t給定時,︿mn(t)、︿m1(t)及︿m2(t)三種方法中︿m1(t)在經驗偏差、經驗標準差及經驗均方誤差三個方面中相對表現最好。 Channing House 數據集是一個左截斷右刪失數據集,經過簡單處理后可以得到一個長度偏差數據子集。因此,近年來經常作為一個長度偏差右刪失數據實例進行研究[10,15]。該數據收集了在1964 年1 月至1975 年7 月期間入住美國Channing House 退休中心的462 名老人的生存數據,包括他們的性別、在該中心登記時的年齡、自登記時起到死亡或直至右刪失事件發生時的持續時間。根據記錄的結果可知,在這462 人中,共有男性97 名和女性365 名,其中有46 名男性和130 名女性于這段隨訪時間內死亡。基于刪失的隨機性和本文研究的長度偏差完全數據,下面我們將以這46 名男性和130 名女性生存數據為例,用以說明文中涉及的三種估計量的應用。 為了從這46 名男性和131 名女性生存數據中獲取一個長度偏差完全數據,借助于文獻[16]中提出的檢驗方法,我們發現死亡時年齡小于79.5 歲的103 人組成的數據集可以看作一個長度偏差完全數據子集,其中該子集中登記時年齡最小的是67.33 歲,這時記A從67.33 歲起至登記時的持續時間,V為從登記時起直至死亡時的持續時間。我們感興趣的是這個子集中的成員隨著時間的推移均值剩余壽命的變化情況。 表3 總結的是Channing House 長度偏差完全數據子集中退休人員在指定年齡的均值剩余壽命的估計值,其中Est 表示均值剩余壽命的點估計,SE 表示由簡單Bootstrap 方法[17]得到的經驗標準差,而CI 表示Bootstrap 置信區間,這里重復抽樣的次數為R=1 000。由表3 中的結果可知,隨著年齡的增加,子集中退休人員的均值剩余壽命是遞減的。這也體現出了文中涉及的估計方法的合理性。 表3 Channing House 數據子集中成員在不同年齡的均值剩余壽命估計 引理2 設D 和E 表示兩個賦范線性空間,映射?: D? ?DE 關于切線方向θ ∈D0?D 是Hadamard-可微的,若存在某序列rn滿足rn ∞時,有 那么rn →∞時,則有 這里Un和U分別為在D?和D0中取值的緊過程。 由于 根據引理2 可得函數γ在(M(t),N(t))處的Hadamard 導數,即有如下引理。 引理3 對于每一個給定的t ∈[0,L],函數γ在(M(t),N(t))處是Hadamard 可導的,且其導數為 引理1 的證明 引理1 的證明已經包含在定理1 的證明中,具體請見定理1 的證明。 定理1 的證明 (i) 因為I(Ti>t),i= 1,2,···,n,相互間是獨立同分布,根據中心極限定理有顯然N︿mn1為兩個高斯變量的線性函數,且因為Z1(t)和Z2(t)為中心對稱的隨機變量,易驗證EN︿m1=0。根據(8)式可得N︿m1的方差為 根據引理3 結論即可得證。2.2 估計方法II
3 漸近性質
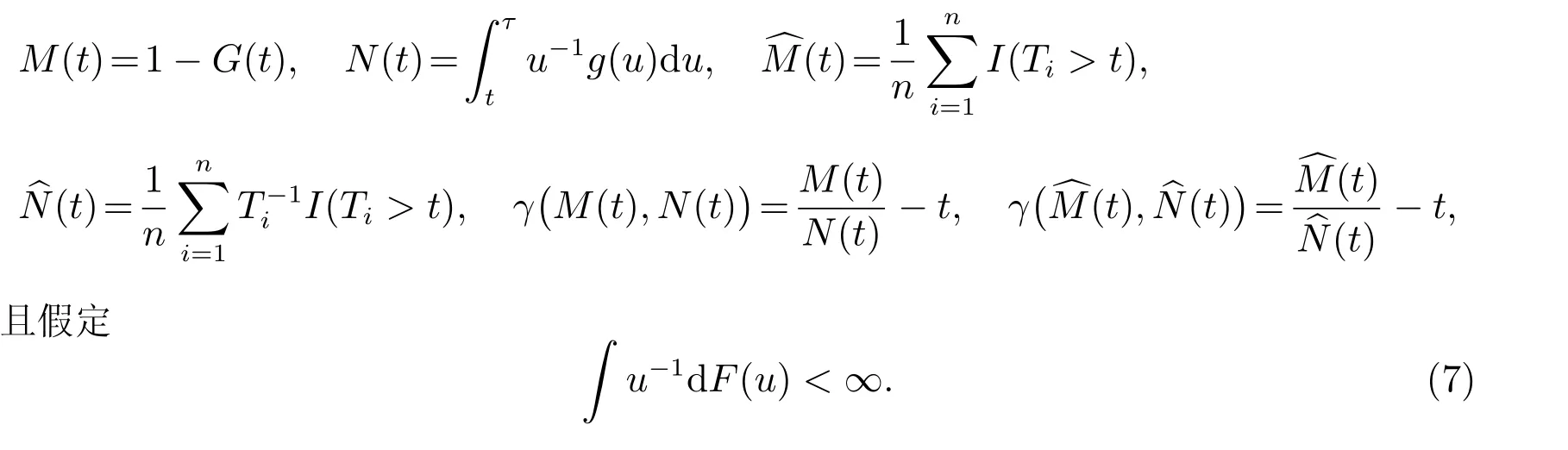
4 數值模擬
5 實際數據
6 引理及定理的證明